
What is the z-score for a 98% confidence interval?
Answer
514.5k+ views
Hint: For solving this type of questions, you should know how to read the standard normal probabilities table. You have to check it carefully for your values. You should find your value or the nearest value of the value you find after getting the confidence $\left( 1-x \right)g100\%$ . We should get the significance before this and then get the critical value.
Complete step by step answer:
In our question it is given that we have to find the z-score $\left( z* \right)$ for the confidence interval of 98%. So, first we have to mark 98% on the graph and then we have to find the tail.
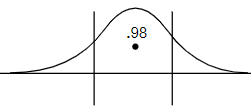
For the tail point of both the tails,
$1-0.98=0.02$
For the tail point of single tail,
$\dfrac{0.02}{2}=0.01$
So, now the values are:
Now, we will use the formula for confidence, that is,
$\left( 1-x \right)g100\%=98\%$
Here, we know, significance is,
$x=0.02$
And then with the help of significance we will be calculating critical value, that is, ${{z}_{x/2}}$.
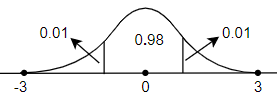
We will now find 0.01 in the ‘df’ row at the top of page $A_{12}$. ${{z}_{x/2}}$ is the last entry in the column under 0.01. The table is given as below.
Hence ${{z}_{x/2}}=2.326$ for 98% confidence.
So, by reading the values in the table and solving this, we get that the z-score of a 98% confidence interval is 2.326.
Note: If your significance value is any value and we by dividing it, we get the values of the tails. And then we check this value in the table or ‘df’ row and if our same value is not available in the table, then we take the nearest value in the table and use the just greater value for getting the answer.
Complete step by step answer:
In our question it is given that we have to find the z-score $\left( z* \right)$ for the confidence interval of 98%. So, first we have to mark 98% on the graph and then we have to find the tail.

For the tail point of both the tails,
$1-0.98=0.02$
For the tail point of single tail,
$\dfrac{0.02}{2}=0.01$
So, now the values are:
Now, we will use the formula for confidence, that is,
$\left( 1-x \right)g100\%=98\%$
Here, we know, significance is,
$x=0.02$
And then with the help of significance we will be calculating critical value, that is, ${{z}_{x/2}}$.

We will now find 0.01 in the ‘df’ row at the top of page $A_{12}$. ${{z}_{x/2}}$ is the last entry in the column under 0.01. The table is given as below.
| z | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.5 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
Hence ${{z}_{x/2}}=2.326$ for 98% confidence.
So, by reading the values in the table and solving this, we get that the z-score of a 98% confidence interval is 2.326.
Note: If your significance value is any value and we by dividing it, we get the values of the tails. And then we check this value in the table or ‘df’ row and if our same value is not available in the table, then we take the nearest value in the table and use the just greater value for getting the answer.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




