Maths Notes for Chapter 13 Statistics Class 11 - FREE PDF Download
FAQs on Statistics Class 11 Maths Chapter 13 CBSE Notes - 2025-26
1. What are the key terms and definitions students must understand for effective revision of Class 11 Statistics Chapter 13?
Some key terms essential for quick revision of Statistics in Class 11 include:
- Statistics: The science of collecting, organizing, presenting, analyzing, and interpreting numerical data.
- Class Interval: The difference between upper and lower class limits in a frequency distribution.
- Primary Data & Secondary Data: Primary is collected by the investigator; secondary is collected by someone else.
- Frequency: The number of times an observation occurs in a dataset.
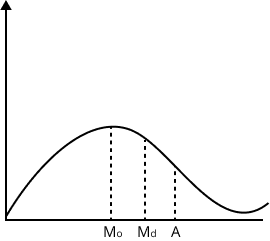
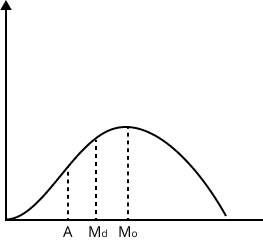
- Mean, Median, Mode: Measures of central tendency that summarize data with a single representative value.
2. How can students structure their chapter-wise revision for Statistics in Class 11 according to the CBSE 2025–26 syllabus?
To revise Statistics Class 11 efficiently as per the current CBSE syllabus, students should:
- Start with understanding core definitions and terms (e.g., mean, median, mode, frequency distributions).
- Quickly review summary tables or concept maps for formulas and graphical methods.
- Practice basic calculations for central tendency and dispersion (mean deviation, standard deviation, variance).
- Interpret and compare different graphical representations (histogram, bar diagram, pie diagram, frequency polygon).
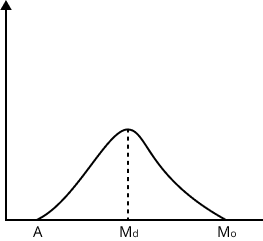
- Recap properties and relationships between measures (e.g., relation between mean, median, mode).
3. What are the main types of frequency distributions and how do they differ?
Frequency distributions in Class 11 Statistics include:
- Discrete frequency distribution: Shows distinct, separate values and their frequencies.
- Continuous frequency distribution: Groups data into intervals, not showing the exact measurements.
- Cumulative frequency distribution: Summarizes frequencies cumulatively across intervals.
The main difference is how data values are presented—discrete for separate values, continuous for interval-based grouping.
4. What is the importance of graphical representation in Statistics revision notes and which types should students master?
Graphical representation is crucial because it helps visualize data trends and frequency distributions quickly for revision. Students should master:
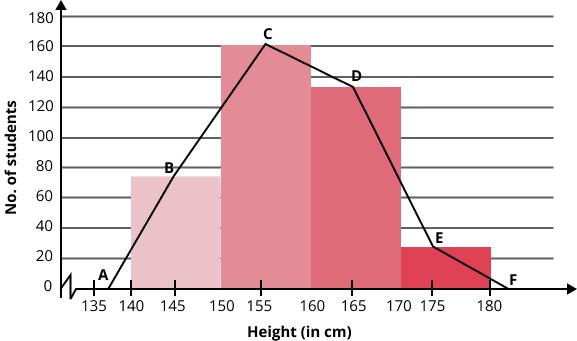
- Histogram – For continuous data.
- Bar diagram – For comparison between discrete categories.
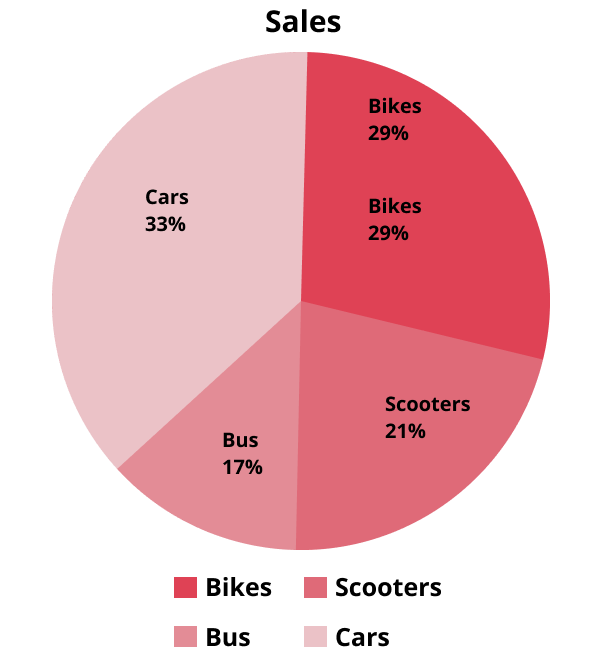
- Pie diagram – For proportions and relative frequency.
- Frequency polygon – For ungrouped distributions.
- Ogive (Cumulative frequency curve) – For understanding cumulative frequencies.
5. How do measures of central tendency (mean, median, mode) help summarise data in Statistics Class 11?
Measures of central tendency like mean, median, and mode provide a single value that describes the center or typical value of a dataset. They simplify complex data and help in quick decision making during revision. Each measure is suitable for different types of data and distributions.
6. What are the different methods to calculate arithmetic mean for various data types found in CBSE Class 11 Statistics?
Arithmetic mean can be calculated using several methods:
- For unclassified data: Add all values and divide by total number of values.
- For frequency distribution: Multiply each value by its frequency, sum these, then divide by total frequency.
- For classified data: Use class marks and frequencies to find the mean.
- Step deviation and assumed mean methods can simplify calculations for large or grouped data.
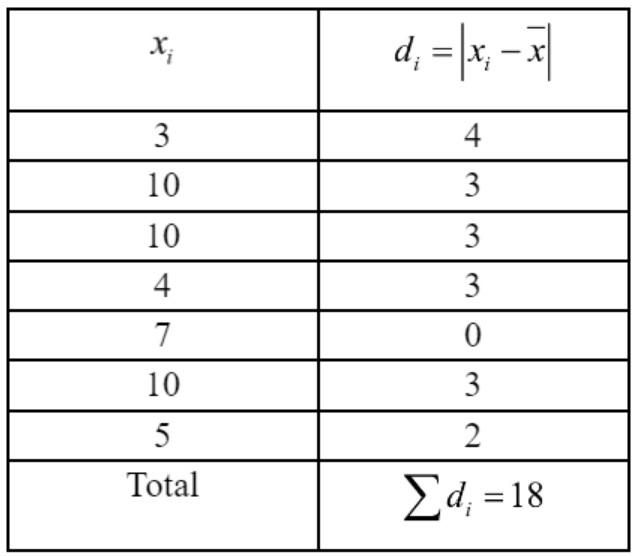
7. What is mean deviation in Statistics and how does it differ from standard deviation?
Mean deviation is the average of the absolute differences between data points and a central value (mean, median, or mode). Standard deviation measures how much values deviate from the mean using squares of differences, making it more sensitive to outliers. Both quantify dispersion, but standard deviation is more widely used and has key formula properties.
8. How can understanding properties of measures like mean and variance prevent common mistakes during revision?
Knowing the properties helps avoid misconceptions, such as:
- The sum of deviations from mean is always zero.
- Variance is always non-negative and is minimized when deviations are measured from the mean.
- Arithmetic mean is independent of change of origin, but dependent on change of scale.
Understanding these prevents calculation errors and helps in verifying answers quickly.
9. Why is it important to distinguish between primary and secondary data when revising Statistics notes?
Distinguishing between primary and secondary data clarifies the source and reliability of data. Primary data is first-hand and usually more reliable for analyses, while secondary data may already be summarized or altered. This awareness improves data interpretation during quick revision and applications in exam questions.
10. How can students revise formulas and properties efficiently before CBSE exams for Statistics Class 11 Chapter 13?
Students should create summary sheets or concept maps of all core formulas, such as those for mean, median, mode, standard deviation, and variance. Practice applying each formula to examples. Use mnemonic aids, flashcards, or teach-back methods to reinforce retention. Regular short revisions just before exams are also recommended for quick recall.
11. What are some application-based questions students should prepare to answer after revising Statistics Class 11 notes?
After revision, students should be able to:
- Calculate the mean, median, and mode for real datasets or exam samples.
- Interpret and draw different graphs based on given data.
- Compare data distributions using standard deviation and variance concepts.
- Identify the type of frequency distribution in practical cases.
- Analyze the significance and consistency of different datasets.