Physics Notes for Chapter 3 Motion In A Plane Class 11 - FREE PDF Download
FAQs on Motion In A Plane Class 11 Physics Chapter 3 CBSE Notes - 2025-26
1. What are the main concepts to quickly revise in the Class 11 chapter on Motion in a Plane?
When revising 'Motion in a Plane', focus on these core concepts for a quick summary:
- Scalars and Vectors: The fundamental difference, including definitions of position and displacement vectors.
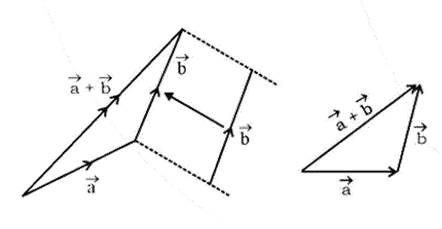
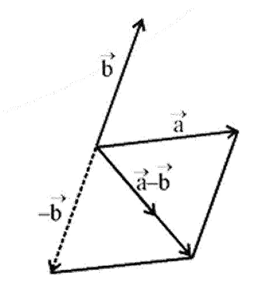
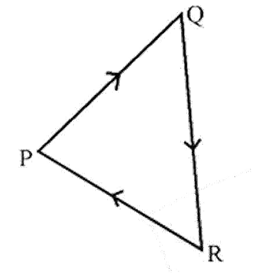
- Vector Operations: Quick revision of vector addition (Triangle and Parallelogram Laws), subtraction, and resolution of vectors into components.
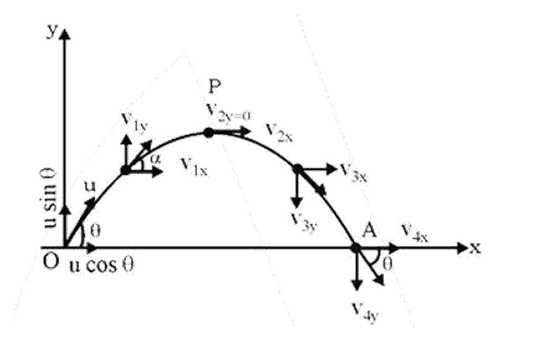
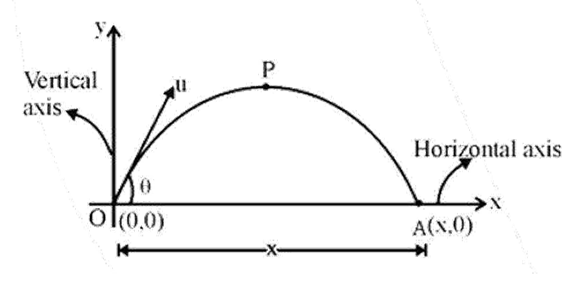
- Projectile Motion: Key formulas for time of flight, maximum height, and horizontal range.
- Uniform Circular Motion: Concepts of angular velocity, angular acceleration, and centripetal acceleration.
- Relative Velocity: Understanding how to calculate the velocity of one object with respect to another in a 2D plane.
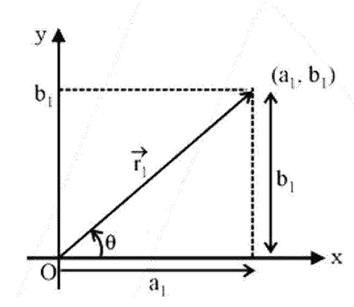
2. What is the key difference between a position vector and a displacement vector?
The key difference lies in their reference point. A position vector specifies an object's location with respect to a fixed origin (e.g., point P is at vector r from the origin). In contrast, a displacement vector represents the change in position. It is a straight line drawn from an object's initial position to its final position, independent of the origin.
3. For revision, why is resolving a vector into its components so important in this chapter?
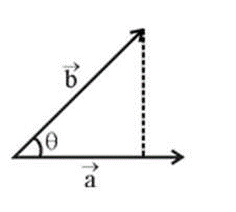
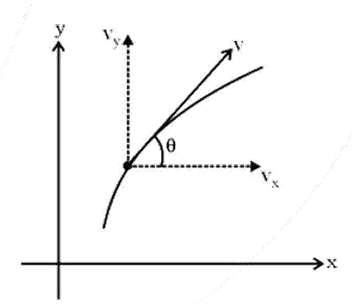
Resolving a vector into its components is a crucial revision technique because it simplifies complex two-dimensional problems. By breaking a vector (like force or velocity) into two perpendicular components (usually along the x and y-axes), you can treat a single 2D motion problem as two separate and much simpler one-dimensional motion problems. This is the fundamental method used to analyse projectile motion.
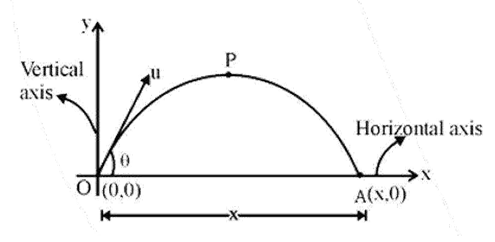
4. What physical quantities remain constant during projectile motion, and which ones change?
This is a critical point to remember for exams. During projectile motion (neglecting air resistance):
- Constant Quantities: The horizontal component of velocity (vₓ) remains constant because there is no horizontal acceleration. The acceleration due to gravity (g) is also constant in both magnitude and direction (downwards).
- Changing Quantities: The vertical component of velocity (vᵧ), the overall speed, the direction of motion, and the kinetic and potential energy all change continuously throughout the trajectory.
5. How can I quickly recall the formula for the range of a projectile fired at an angle θ?
To quickly recall the formula for the horizontal range (R), remember it depends on the total time of flight and the constant horizontal velocity. The formula is R = (u² sin(2θ)) / g. A key tip for revision is to remember that the range is maximum when the launch angle θ is 45°, as sin(2θ) becomes sin(90°), which is 1.
6. What is the difference between uniform and non-uniform circular motion?
The key difference is in the speed of the object. In uniform circular motion, the object moves at a constant speed, so its tangential acceleration is zero. However, its velocity is constantly changing direction, so there is a centripetal acceleration. In non-uniform circular motion, the object's speed changes, meaning it has both a centripetal acceleration (to change direction) and a tangential acceleration (to change speed).
7. What is the relationship between linear velocity (v) and angular velocity (ω) in circular motion?
The relationship between linear velocity (v) and angular velocity (ω) for an object moving in a circle of radius (r) is given by the vector equation v = ω × r. For a quick magnitude check during revision, the formula simplifies to v = rω. This shows that the linear speed is directly proportional to both the radius of the circular path and the angular velocity.
8. Why is relative velocity in a plane often handled using vector subtraction?
Relative velocity is handled using vector subtraction because it fundamentally describes the velocity of one object as seen from the perspective of another moving object. The velocity of object B relative to object A (v_BA) is found by subtracting the velocity of the observer (A) from the velocity of the observed object (B). The formula v_BA = v_B - v_A mathematically represents this shift in the frame of reference.
9. How do the concepts from 'Motion in a Straight Line' apply to this chapter?
The concepts from 'Motion in a Straight Line' are the building blocks for 'Motion in a Plane'. The three main equations of motion (v = u + at, s = ut + ½at², and v² = u² + 2as) are applied independently to the horizontal and vertical components of motion. For projectile motion, these equations are used for the vertical motion (with a = g) and simplified for the horizontal motion (with a = 0).