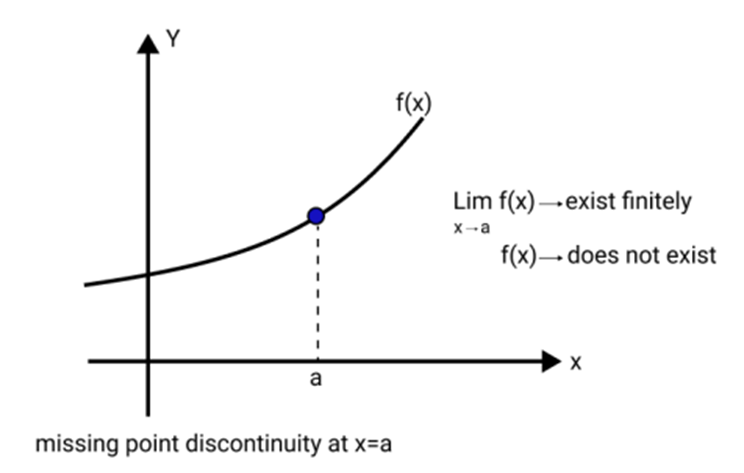
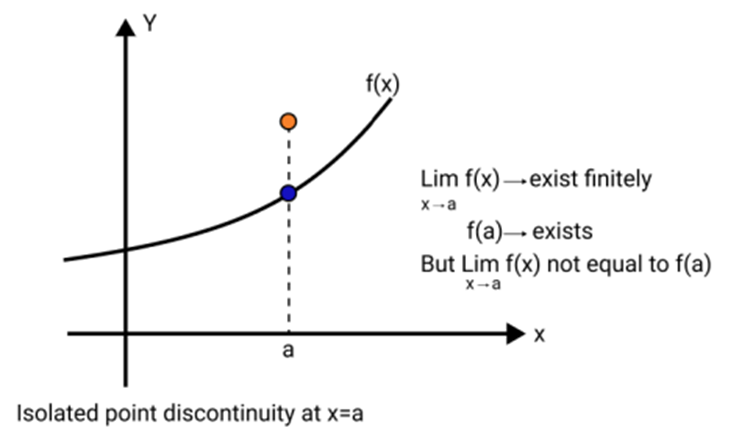
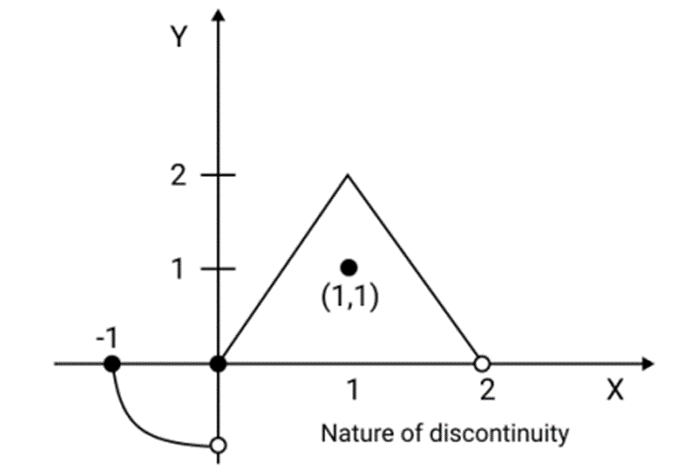
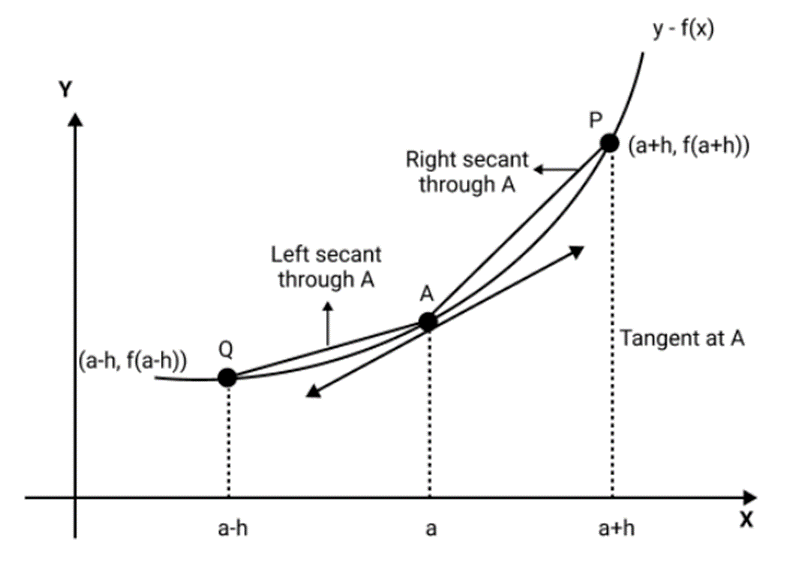
Class 12 Maths Chapter 5 Continuity and Differentiability Notes FREE PDF Download









FAQs on Continuity and Differentiability Class 12 Notes: CBSE Maths Chapter 5
1. What topics are covered in the Continuity and Differentiability Class 12 notes?
The Continuity and Differentiability Class 12 notes cover essential topics such as the definitions of continuity and differentiability, conditions for continuity at a point, derivative rules, higher-order derivatives, and applications of the chain rule.
2. How can the Continuity and Differentiability notes help in exam preparation?
The Continuity and Differentiability notes provide clear explanations, important formulas, and solved examples that simplify complex concepts, making them ideal for thorough exam preparation.
3. Where can I download the Continuity and Differentiability Class 12 notes PDF?
You can download the Continuity and Differentiability Class 12 notes PDF from Vedantu, which offer these notes for free to help students in their studies.
4. Are the Continuity and Differentiability Class 12 notes PDF comprehensive enough for board exam preparation?
Yes, the Continuity and Differentiability Class 12 notes PDF are designed to comprehensively cover the entire syllabus, making them an excellent resource for board exam preparation.
5. Do the Continuity and Differentiability notes include solved examples?
Yes, the Continuity and Differentiability notes typically include a variety of solved examples that demonstrate the application of concepts and formulas, helping students understand how to approach different types of problems.
6. Can I use the Continuity and Differentiability Class 12 notes for competitive exam preparation?
Absolutely! The Continuity and Differentiability Class 12 notes are aligned with the syllabus of many competitive exams, providing a strong foundation for solving calculus-related questions.
7. How often should I revise using the Continuity and Differentiability notes PDF?
Regular revision using the Continuity and Differentiability notes PDF is recommended to keep the concepts and formulas fresh in your memory, especially as you approach your exams.
8. Are the Continuity and Differentiability Class 12 notes useful for last-minute revision?
Yes, the Continuity and Differentiability Class 12 notes are structured to be concise and focused, making them ideal for last-minute revision. They highlight all the key concepts and formulas needed for the exam.
9. Where can I find high-quality Continuity and Differentiability notes PDF for free?
High-quality Continuity and Differentiability notes PDF can be found on Vedantu, which provide comprehensive study materials and notes for free download.
10. What are the key benefits of using Continuity and Differentiability Class 12 notes?
The key benefits include simplified explanations of complex concepts, easy access to important formulas, step-by-step problem-solving techniques, and the ability to revise quickly before exams.