NCERT Exemplar for Class 12 Chemistry Chapter-4 (Book Solutions)

I. MULTIPLE CHOICE QUESTIONS (TYPE-I)

1. The role of a catalyst is to change ______.

A.  Gibbs energy of reaction

B.  enthalpy of reaction

C.  activation energy of reaction                                                         

D.  equilibrium constant

Ans: Option C

Gibbs energy of reaction - Gibbs free energy is a single-valued combination of entropy and enthalpy. The direction of a chemical reaction at constant temperature and pressure is predicted by Gibbs free energy.

Enthalpy of reaction – When one mole of matter is converted by a chemical reaction under specified conditions, the enthalpy of reaction is the change that occurs in the system.

Activation energy of reaction – The lowest amount of energy necessary to activate molecules to a state where they can perform physical and chemical transformations is known as the activation energy of a process. The catalyst creates a lower-activation-energy pathway.

Equilibrium constant – The equilibrium constant is denoted by the letter "K." It is the equilibrium relationship between the products and reactants of a reaction in terms of a specified unit.

2. In the presence of a catalyst, the heat evolved or absorbed during the reaction _____.

A.  increases

B.  decreases

C.  remains unchanged

D.  may increase or decrease

Ans: Correct option:  C

A catalyst allows a chemical reaction to occur at a faster rate or under different conditions than it would otherwise. As a result, a catalyst affects the reaction's enthalpy change, or heat. As a result, in the presence of the reaction, the enthalpy does not vary, i.e., it remains constant, and no heat is produced or absorbed.

3. Activation energy of a chemical reaction can be determined by ________.

A.  determining the rate constant at standard temperature

B.  determining the rate constants at two temperatures

C.  determining probability of collision

D.  using catalyst

Ans: Correct option: B

The Arrhenius equation can be used to calculate the activation energy of a chemical process. At two temperatures, this determines the rate constants.

\[{\text{2}}{\text{.303log}}\dfrac{{{{\text{K}}_{\text{2}}}}}{{{{\text{K}}_{\text{1}}}}}{\text{ = }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{\text{R}}}\left[ {\dfrac{{{{\text{T}}_{\text{2}}}{\text{ - }}{{\text{T}}_{\text{1}}}}}{{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}}}} \right]\]

4. Consider Fig. 4.1 and mark the correct option.

A. Activation energy of forward reaction is \[{{\text{E}}_{\text{1}}}{\text{ + }}{{\text{E}}_{\text{2}}}\]and product is less stable than reactant.

B. Activation energy of forward reaction is \[{{\text{E}}_{\text{1}}}{\text{ + }}{{\text{E}}_{\text{2}}}\]and product is more stable than reactant.

C.Activation energy of both forward and backward reaction is\[{{\text{E}}_{\text{1}}}{\text{ + }}{{\text{E}}_{\text{2}}}\] and reactant is more stable than product.

D.  Activation energy of backward reaction is \[{{\text{E}}_{\text{1}}}\]and product is more stable than reactant.

Ans: Correct option A

Activation Energy \[ \to \] The amount of energy required to overcome the obstacle and generate a product

The activation energy of a forward reaction can be seen in the \[\left[ {{{\text{E}}_{{\text{af}}}}{\text{ = }}{{\text{E}}_{\text{1}}}{\text{ + }}{{\text{E}}_{\text{2}}}} \right]\] (This is an endothermic reaction.

Therefore, \[\left[ {{{\text{E}}_{{\text{af}}}}{\text{ > }}{{\text{E}}_{{\text{ab}}}}} \right]\]   

The energy of the product is high, while the energy of the reactant is low.

The lower the energy, the more stable and positive the situation becomes.

\[{\text{}\Delta{ h  =  positive}}\].

5. Consider a first order gas phase decomposition reaction given below:

\[{\text{A}}\left( {\text{g}} \right){\text{ }} \to {\text{ B}}\left( {\text{g}} \right){\text{ + C}}\left( {\text{g}} \right){\text{ }}\]

The initial pressure of the system before decomposition of \[{\text{A}}\] was\[{{\text{p}}_{\text{t}}}\] . After lapse of time ‘\[t\]’, total pressure of the system increased by \[{\text{x}}\] units and became ‘\[{\text{t}}\]’ the rate constant \[{\text{k}}\] for the reaction is given as _________.

A.  \[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\text{p}}_{\text{t}}}}}{{{{\text{p}}_{\text{t}}}{\text{ - x}}}}\]

B.   \[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\text{p}}_{\text{t}}}}}{{{\text{2}}{{\text{p}}_{\text{t}}}{\text{ - }}{{\text{p}}_{\text{t}}}}}\]

C.   \[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\text{p}}_{\text{t}}}}}{{{\text{2}}{{\text{p}}_{\text{t}}}{\text{ + }}{{\text{p}}_{\text{t}}}}}\]

D.   \[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\text{p}}_{\text{t}}}}}{{{\text{2}}{{\text{p}}_{\text{t}}}{\text{ + x}}}}\]

Ans: Correct option B

Given:  

\[{\text{A}}\left( {\text{g}} \right) \to {\text{B}}\left( {\text{g}} \right){\text{ + C}}\left( {\text{g}} \right){\text{ }}\]

\[{p_i} = \] Initial pressure

(Time) \[{\text{t = 0}}\]

\[{\text{A}}\left( {\text{g}} \right){\text{ }} \to {\text{ B}}\left( {\text{g}} \right){\text{ + C}}\left( {\text{g}} \right){\text{ }}\]

\[{{\text{p}}_{\text{i}}} \to {{\text{0}}_{{\text{atm}}}}{\text{ + }}{{\text{0}}_{{\text{atm}}}}\]

\[{\text{t,(}}{{\text{p}}_{\text{i}}}{\text{ - x)atm}}\]

\[{{\text{p}}_{\text{t}}}{\text{ = (}}{{\text{p}}_{{\text{i}}}}{\text{ - x)atm}}{\text{ + x + x = }}{{\text{p}}_{{\text{i}}}}{\text{ + x}}\]

\[{{\text{p}}_{\text{A}}}{\text{ = (}}{{\text{p}}_{\text{i}}}{\text{ - x)}}\]

The value of x changes when it is substituted.

\[{{\text{p}}_{\text{A}}}{\text{ = }}{{\text{p}}_{\text{i}}}{\text{ - (}}{{\text{p}}_{\text{t}}}{\text{ - }}{{\text{p}}_{\text{i}}}{\text{) = 2}}{{\text{p}}_{\text{i}}}{\text{ - }}{{\text{p}}_{\text{t}}}\]

\[{\text{K = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\text{p}}_{\text{i}}}}}{{{\text{2}}{{\text{p}}_{\text{i}}}{\text{ - }}{{\text{p}}_{\text{t}}}}}\]

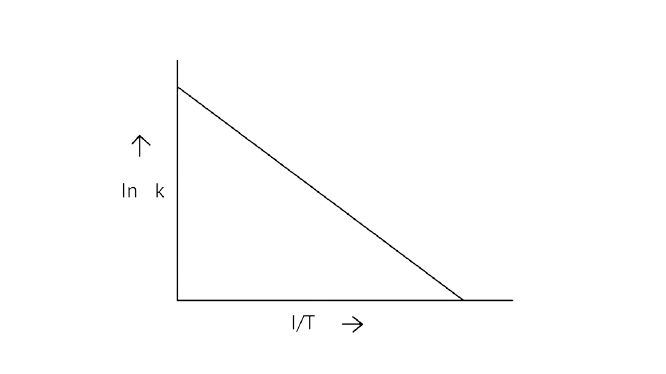
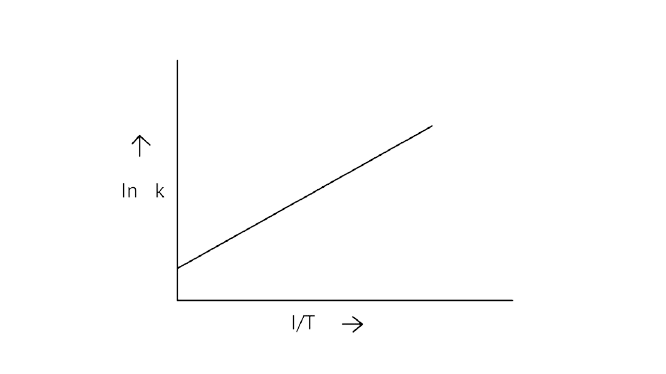
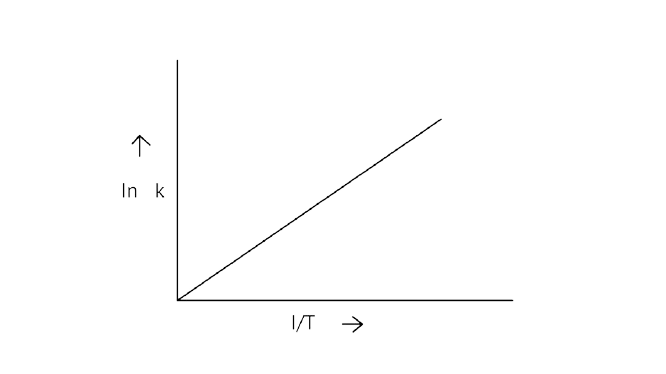
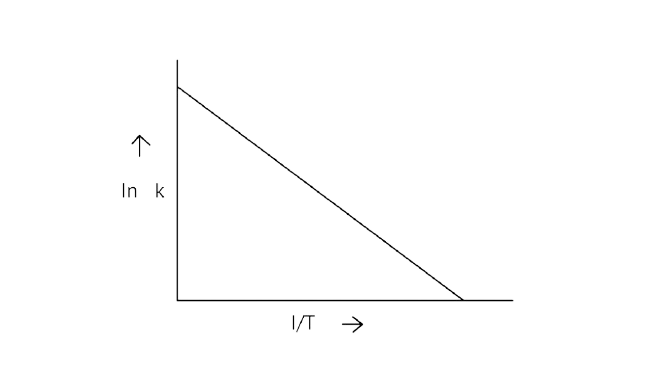
6. According to Arrhenius equation rate constant \[{\text{k}}\] is equal to \[{\text{Ae - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]. Which of the following options represents the graph of in \[{\text{k vs}}\dfrac{{\text{1}}}{{\text{T}}}\]?

A.

B.

C.

D. 

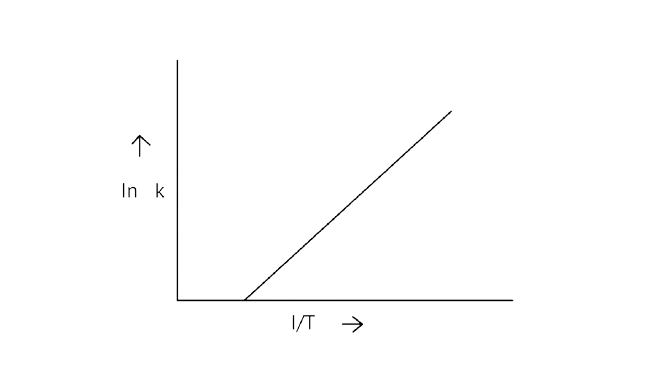
Ans: Correct option A

Arrhenius equation \[{\text{Ae - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]

\[k\] = rate constant

\[A\]= frequency factor

\[{E_a}\]= Activation Energy

\[R\]= gas constant

\[T\]= temperature

\[{\text{ln k = lnA - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]

When the temperature rises, ${\text{ln}}$ falls.

$\;\;\therefore $ \[{\text{ln k}}\]v/s \[\dfrac{{\text{1}}}{{\text{T}}}\], is a negative slope.

\[{\text{ln A}}\] is intercepted by ${\text{k}}$, and its magnitude decreases with time.

$\therefore $ Negative slope is obtained.

When compared to the other possibilities, T is increasing over time, which is incorrect.

\[{\text{ln k = }}\dfrac{{{\text{ - }}{{\text{E}}_{\text{a}}}}}{{\text{R}}}\dfrac{{\text{1}}}{{\text{T}}}{\text{ + lnA}}\]

7. Consider the Arrhenius equation given below and mark the correct option.

\[{\text{k = Ae - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]

A. Rate constant increases exponentially with increasing activation energy and decreasing  temperature.

B.  Rate constant decreases exponentially with increasing activation energy and decreasing temperature. 

C.  Rate constant increases exponentially with decreasing activation energy and decreasing temperature.

D. Rate constant increases exponentially with decreasing activation energy and increasing temperature.

Ans: Correct option D

\[{\text{k = Ae - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]

From this equation

\[{{k\alpha }}\dfrac{{\text{1}}}{{{{\text{E}}_{\text{a}}}}}\]

\[{{k\alpha T}}\]

When Activation energy \[{{\text{E}}_{\text{a}}}\] decreases, rate constant ${\text{k}}$ increases.

Hence, Rate constant increases exponentially with decreasing activation energy and increasing temperature. 

8. A graph of volume of hydrogen released vs time for the reaction between zinc and dil. HCl is given in Fig. 4.2. Based on this mark the correct option   

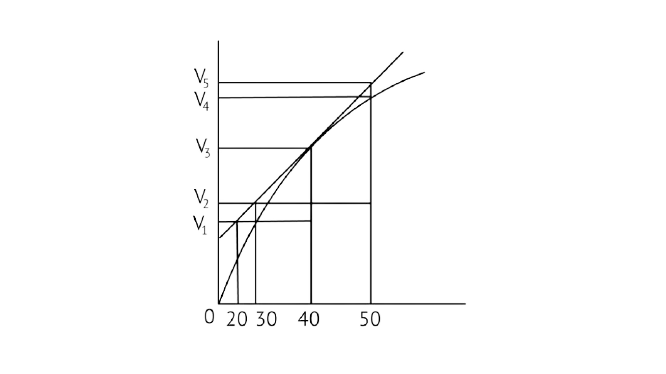
                                      Fig. 4.2          

A. Average rate up to 40s is \[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - }}{{\text{V}}_{\text{2}}}}}{{{\text{40}}}}\]

B. Average rate up to 40 seconds is \[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - }}{{\text{V}}_{\text{2}}}}}{{{\text{40 - 30}}}}\]

C. Average rate up to 40 seconds is \[\dfrac{{{{\text{V}}_{\text{3}}}}}{{{\text{40}}}}\]

D. Average rate up to 40 seconds is \[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - }}{{\text{V}}_{\text{1}}}}}{{{\text{40 - 20}}}}\]

 Ans: Correct option C

In the given graph ${\text{V}}$ is the volume in the Y axis and time is in X axis

\[{\text{Zn + dil}}{\text{.HCl}} \to {\text{ZnC}}{{\text{l}}_{\text{2}}}{\text{ + }}{{\text{H}}_{\text{2}}} \uparrow \]

Average rate = 40s

\[{\text{Average rate in reaction = }}\dfrac{{{\text{Change in concentration of }}{{\text{H}}_{\text{2}}}}}{{{\text{Change in time}}}}\]

\[\dfrac{{{\text{Final concentration  -  Initial concentration}}}}{{{\text{Final time  -  Initial time}}}}\]

Analyzing the graph line where time and volume intersect. 

\[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - 0}}}}{{{\text{40 - 0}}}}\]

\[\dfrac{{{{\text{V}}_{\text{3}}}}}{{{\text{40}}}}\]

9. Which of the following statements is not correct about order of a reaction

A. The order of a reaction can be a fractional number.

B. Order of a reaction is experimentally determined quantity.

C. The order of a reaction is always equal to the sum of the stoichiometric coefficients of reactants in the balanced chemical equation for a reaction.

D. The order of a reaction is the sum of the powers of molar concentration of the reactants in the rate law expression. 

Ans: Correct option C

Option (c) is the only one of the four assertions that is incorrect. In rate law expression, the order of reaction is equal to the sum of the power of concentration of the reactants.

${\text{xA + yB}} \to {\text{zC}}$

${\text{r = k(A}}{{\text{)}}^{\text{x}}}{{\text{(B)}}^{\text{y}}}$ 

Order \[{\text{x + y}}\]

The order of the reactions can also be a fraction. In a balanced chemical equation, the order of reaction may or may not be equal to the total of the stoichiometric coefficients of the reactants.

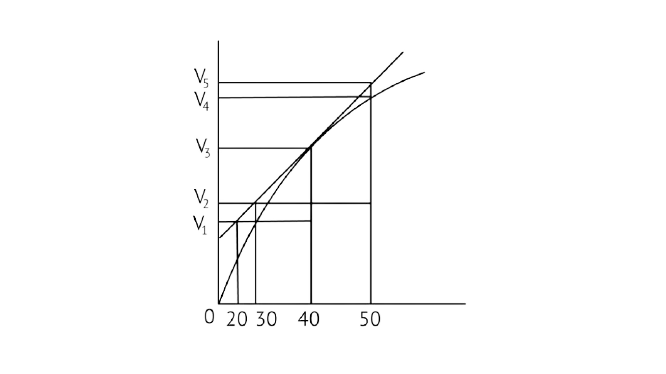
10. Consider the graph given in Fig. 4.2. Which of the following options does not show instantaneous rate of reaction at ${40^{th}}$ second?

A. \[\dfrac{{{{\text{V}}_{\text{5}}}{\text{ - }}{{\text{V}}_{\text{2}}}}}{{{\text{50 - 30}}}}\]

B. \[\dfrac{{{{\text{V}}_{\text{4}}}{\text{ - }}{{\text{V}}_{\text{2}}}}}{{{\text{50 - 30}}}}\]

C. \[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - }}{{\text{V}}_{\text{2}}}}}{{{\text{40 - 30}}}}\]

D. \[\dfrac{{{{\text{V}}_{\text{3}}}{\text{ - }}{{\text{V}}_{\text{1}}}}}{{{\text{40 - 20}}}}\]

Ans: Correct option B

Reaction occurring at the smallest time interval is known as instantaneous rate of reaction. For e.g the instantaneous rate of reaction at 40s is the rate of reaction during a small interval of time close to 40s. Volume changes during a small-time interval close to the 40s.

Instantaneous rate can be determined graphically by drawing a tangent on the curve

Instantaneous reaction=\[\dfrac{{{\text{change in concentration}}}}{{{\text{change in time}}}}\]

Option B is incorrect since the line travels through the graph but does not link to any of the Y axis lines. As a result, option B is incorrect.

11. Which of the following statements is correct?

A. The rate of a reaction decreases with passage of time as the concentration of reactants decreases.

B. The rate of a reaction is same at any time during the reaction.

C. The rate of a reaction is independent of temperature change.

D. The rate of a reaction decreases with increase in concentration of reactants.

Ans: Correct option  A

Because reactant concentrations fall as reactants are transformed to products, reaction rates decrease over time. When reactant concentrations are raised, reaction rates generally increase.

12. Which of the following expressions is correct for the rate of reaction given below?

\[{\text{5Br - (aq) + Br}}{{\text{O}}^{\text{3}}}{\text{ - (aq) + 6H + (aq)}} \to {\text{3B}}{{\text{r}}^{\text{2}}}{\text{(aq) + 3}}{{\text{H}}_{\text{2}}}{\text{O(l)}}\]

A.  \[\dfrac{{{{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{{}\Delta{ }}}{\text{ = 5}}\dfrac{{{{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{{}\Delta{ t}}}}\]

B. \[\dfrac{{{{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{{}\Delta{ }}}{\text{ = }}\dfrac{{\text{6}}}{{\text{5}}}\dfrac{{{{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{\text{}\Delta{ t}}}}\]

C. \[\dfrac{{{\text{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{\text{}\Delta{ }}}{\text{ = }}\dfrac{{\text{5}}}{{\text{6}}}\dfrac{{{\text{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{\text{}\Delta{ t}}}}\]

D. \[\dfrac{{{\text{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{\text{}\Delta{ }}}{\text{ = 6}}\dfrac{{{\text{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{\text{}\Delta{ t}}}}\]

Ans: Correct option C

Rate of Disappearance = \[\dfrac{{{\text{ - 1}}}}{{\text{5}}}\dfrac{{{\text{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{\text{}\Delta{ }}}{\text{ =   -  }}\dfrac{{{\text{}\Delta{ }}\left[ {{\text{Br}}{{\text{O}}^{\text{ - }}}{\text{3}}} \right]}}{{{\text{}\Delta{ t}}}}{\text{  =  }}\dfrac{{{\text{ - 1}}}}{{\text{6}}}\dfrac{{{\text{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{\text{}\Delta{ t}}}}\]

\[\dfrac{{{\text{}\Delta{ }}\left[ {{\text{Br}}} \right]}}{{\text{}\Delta{ }}}{\text{ = }}\dfrac{{\text{5}}}{{\text{6}}}\dfrac{{{\text{}\Delta{ }}\left[ {{{\text{H}}^{\text{ + }}}} \right]}}{{{\text{}\Delta{ t}}}}\]

13. Which of the following graphs represents exothermic reaction?

A.

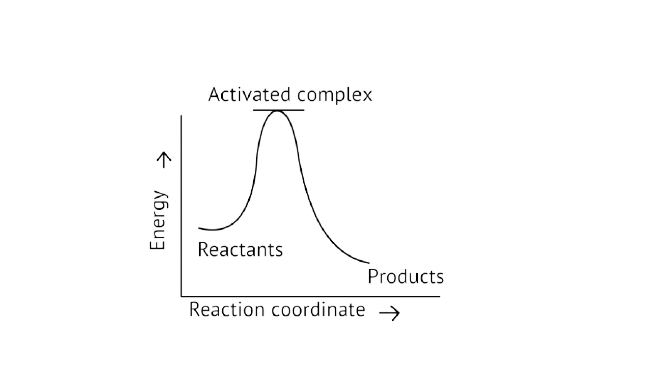
B.

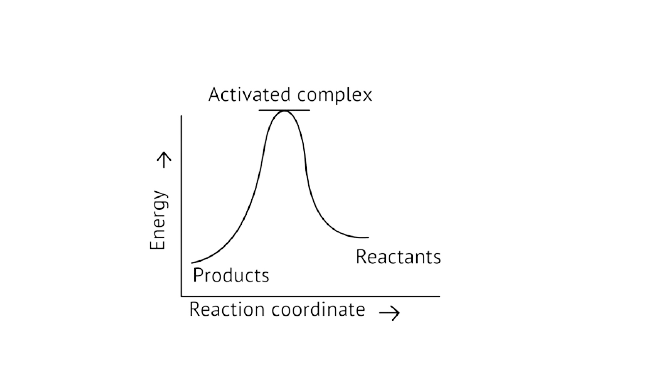
C.

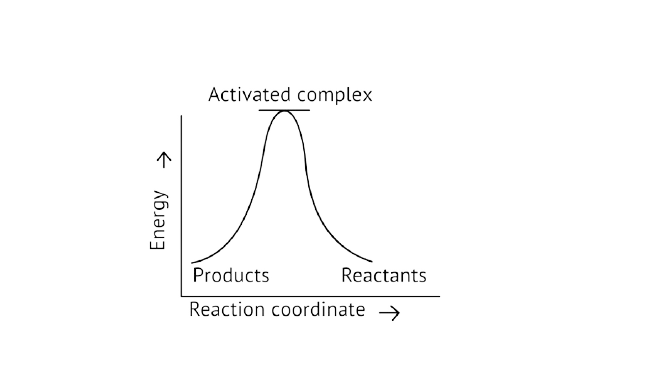
A. (a) only

B. (b) only

C. (c) only

D. (a) and (b) only

Ans: Correct option A

Exothermic Reaction: Exothermic reaction is a chemical reaction in which the enthalpy change is negative, and energy is released in the form of light and heat.

As we all know, \[{\text{}\Delta{ H}}\] is negative.

Activation energy (forward reaction) – (backward reaction)

\[\left( {{\text{Forward reaction}}} \right){\text{  - }}{{\text{E}}_{\text{a}}}\left( {{\text{backward reaction}}} \right)\] 

The product's exothermic energy exceeds the activation energy of the reactants, therefore the correct answer is A, or graph 1, which depicts an exothermic reaction.

14. Rate law for the reaction \[{\text{A + 2B}} \to {\text{C}}\] is found to be  

\[{\text{Rate = k}}\left[ {\text{A}} \right]\left[ {\text{B}} \right]\]          

Concentration of reactant ‘B’ is doubled, keeping the concentration of ‘A’ constant, the value of rate constant will be______.

A. the same

B. doubled

C. quadrupled

D. halved

Ans: Correct option A

The rate concentration of a reaction does not depend upon concentrations of the reactions. Hence, it will remain the same. Even if the equation shows the double concentration level even the rate concentration doubles so it’s the same throughout.

Following with the equation 

\[{\text{A + 2B}} \to {\text{C}}\]

If rate considered as (1)

\[{\text{Rat}}{{\text{e}}_{\text{1}}}{\text{ = k}}\left[ {\text{A}} \right]\left[ {\text{B}} \right]\]

If rate considered as 2

Then, \[{\text{Rat}}{{\text{e}}_{\text{1}}}{\text{ = k}}\left[ {\text{A}} \right]\left[ {{\text{2B}}} \right]\]      

\[{\text{Rat}}{{\text{e}}_{\text{2}}}{\text{ = 2Rat}}{{\text{e}}_{\text{1}}}\]     

Option A is correct answer

15. Which of the following statements is incorrect about the collision theory of chemical reaction?

A. It considers reacting molecules or atoms to be hard spheres and ignores their structural features. 

B. Number of effective collisions determines the rate of reaction.

C. Collision of atoms or molecules possessing sufficient threshold energy results into the product formation.

D. Molecules should collide with sufficient threshold energy and proper orientation for the collision to be effective.

Ans: Correct option C

In the case of gases, collision theory is used to predict the speeds of chemical processes. According to this idea, the reacting chemicals must collide with enough energy and in the right direction. The molecules travel quicker and the frequency increases as the temperature rises.

This proves that all three other possibilities, A, B, and D, are correct. Option C does not correspond to the correct answer.

16. A first order reaction is 50% completed in ${\text{1}}{\text{.26 }\times{ 1}}{{\text{0}}^{{\text{14}}}}{\text{s}}$. How much time would it take for 100% completion?

A. \[{\text{1}}{\text{.26 }\times{ 1}}{{\text{0}}^{{\text{15}}}}{\text{s}}\]

B. \[{\text{2}}{\text{.52 }\times{ 1}}{{\text{0}}^{{\text{14}}}}{\text{s}}\]

C. \[{\text{2}}{\text{.52 }\times{ 1}}{{\text{0}}^{{\text{28}}}}{\text{s}}\]

D. infinite

Ans: Correct option D

Note. It is not possible to perform 100% of the reaction because is half-life.

Basically, it is called half-line period of the reaction. So, the time taken for 100% completion of the reaction is infinite.

17. Compounds ‘${\text{A}}$’ and ‘${\text{B}}$’ react according to the following chemical equation.

\[{\text{A}}\left[ {\text{g}} \right]{\text{ + 2B}}\left[ {\text{g}} \right] \to {\text{2C}}\]

Concentration of either ‘${\text{A}}$’ or ‘${\text{B}}$’ were changed keeping the concentrations of one of the reactants constant and rates were measured as a function of initial concentration. Following results were obtained. Choose the correct option for the rate equations for this reaction.

A. \[{\text{Rate = k}}{\left[ {\text{A}} \right]^{\text{2}}}\left[ {\text{B}} \right]\]

B. \[{\text{Rate = k}}\left[ {\text{A}} \right]{\left[ {\text{B}} \right]^{\text{2}}}\]

C. \[{\text{Rate = k}}\left[ {\text{A}} \right]\left[ {\text{B}} \right]\]

D. \[{\text{Rate = k}}{\left[ {\text{A}} \right]^{\text{2}}}{\left[ {\text{B}} \right]^{\text{0}}}\]

Ans: Correct option B

Let order of ${\text{A}}$ and ${\text{B}}$ be ${\text{x}}$ and ${\text{y}}$.

\[{\text{r = k}}{\left[ {\text{A}} \right]^{\text{x}}}{\left[ {\text{B}} \right]^{\text{y}}}\]

\[{\text{0}}{\text{.1 = k}}{\left( {{\text{0}}{\text{.3}}} \right)^{\text{x}}}{{\text{(0}}{\text{.3)}}^{\text{y}}}\]_______1

\[{\text{0}}{\text{.4 = 0}}{\text{.1 = k}}{\left( {{\text{0}}{\text{.3}}} \right)^{\text{x}}}{{\text{(0}}{\text{.6)}}^{\text{y}}}\]_______2

\[{\text{0}}{\text{.2 = 0}}{\text{.1 = k}}{\left( {{\text{0}}{\text{.6}}} \right)^{\text{x}}}{{\text{(0}}{\text{.3)}}^{\text{y}}}\]______3

Divide 2 by 1

\[\dfrac{{{\text{0}}{\text{.4}}}}{{{\text{0}}{\text{.1}}}}{\text{ = }}\dfrac{{{{{\text{(0}}{\text{.6)}}}^{\text{y}}}}}{{{{{\text{(0}}{\text{.3)}}}^{\text{y}}}}}\]

Divide 3 by 1

\[\dfrac{{{\text{0}}{\text{.2}}}}{{{\text{0}}{\text{.1}}}}{\text{ = }}\dfrac{{{{{\text{(0}}{\text{.6)}}}^{\text{x}}}}}{{{{{\text{(0}}{\text{.3)}}}^{\text{x}}}}}\]

Hence Rate law is

\[{\text{r = k}}{\left[ {\text{A}} \right]^{\text{1}}}{\left[ {\text{B}} \right]^{\text{2}}}\]

18: Which of the following statements is not correct for the catalyst?

A. It catalyses the forward and backward reaction to the same extent.

B. It alters ∆G of the reaction.

C. It is a substance that does not change the equilibrium constant of a reaction. 

D. It provides an alternate mechanism by reducing activation energy between reactants and products

Ans: Correct option C

In the presence of a catalyst, the value of \[{\text{}\Delta{ G}}\] cannot be changed for any reaction.

\[{\Delta{ G  =   -  Rt ln Q}}\].

Where \[{\text{Q}}\] is the Reaction Quotient, which is determined by the product and reactant concentrations. As a result, \[{\text{}\Delta{ G}}\] has no connection to the catalyst. Only when the reaction is spontaneous, which must be negative, is it checked. As a result, \[{\text{}\Delta{ G}}\] cannot be changed.

19. The value of rate constant of a pseudo first order reaction ____________. 

A. depends on the concentration of reactants present in small amount

B. depends on the concentration of reactants present in excess. 

C. is independent of the concentration of reactants.

D. depends only on temperature. 

Ans: Correct option C

Let's start with what a pseudo-first-order response is.

Although the pseudo-first-order reaction looks to be an order, it belongs to another order. It's a second-order reaction because it involves two reactants.

Let's have a look at a reaction.

\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br + OH}} \to {\text{C}}{{\text{H}}_{\text{3}}}{\text{OH + B}}{{\text{r}}^{\text{ - }}}\]

So, the rate law for the reaction is

\[{\text{Rate = k}}\left[ {{\text{OH}}} \right]\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br}}} \right]\]

\[{\text{Rate = k}}\left[ {{\text{O}}{{\text{H}}^{\text{ - }}}} \right]\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br}}} \right]{\text{ = k(constant)}}\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br}}} \right]{\text{ = K'}}\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br}}} \right]\]

Only the concentration of \[{\text{C}}{{\text{H}}_{\text{3}}}{\text{Br}}\] will change during the reaction, and the rate will be determined by the reaction's modifications.

20. Consider the reaction ${\text{A}} \rightleftharpoons {\text{B}}$. The concentration of both the reactants and the products varies exponentially with time. Which of the following figures correctly describes the change in concentration of reactants and products with time?

A.

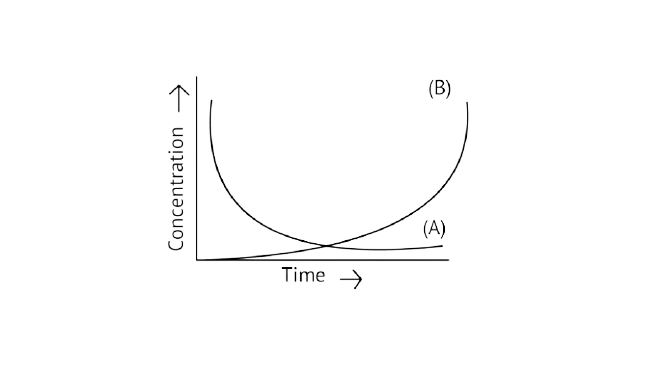
B.

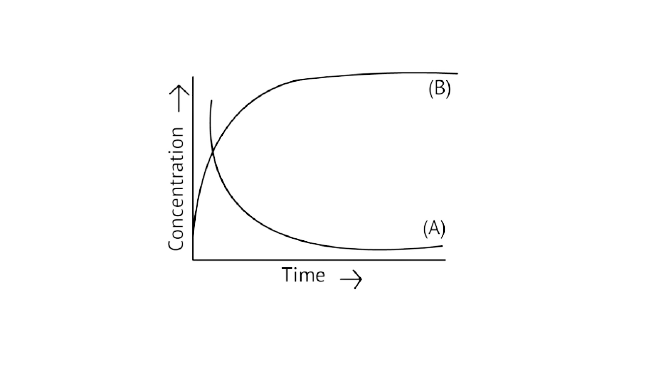
C.

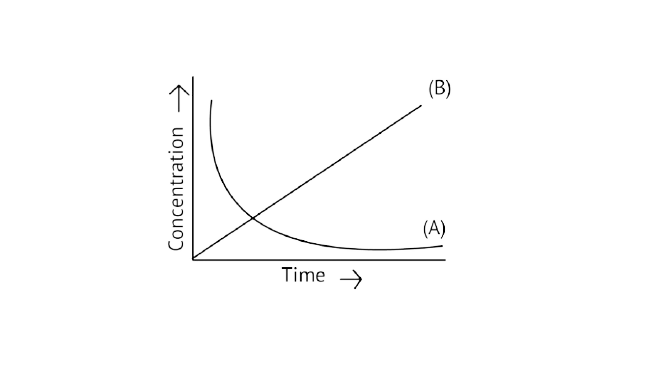
D.

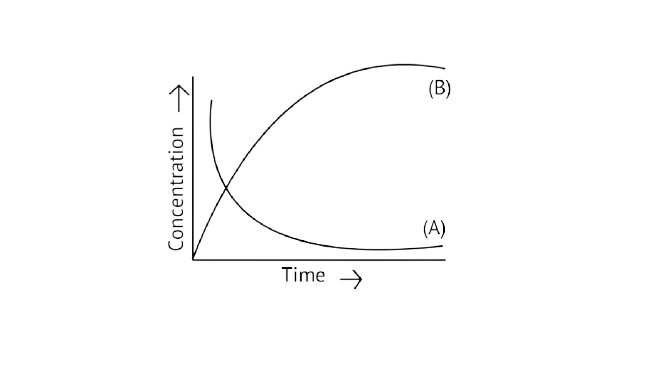
Ans: Correct option B

If ${\text{A}} \to {\text{B}}$ then the concentration of both reactants and the products vary exponentially with time. But, in option B graph the reactant concentration decreases exponentially and the product concentration increases.

II. Multiple Choice Questions (Type-II)

Note. In the following questions two or more options may be correct.

21. Rate law cannot be determined from balanced chemical equation if _______.

A. reverse reaction is involved.

B. it is an elementary reaction.

C. it is a sequence of elementary reactions. 

D. any of the reactants is in excess

Ans: Correct options : A, C and D.

Rate law = Experimental rate of the reaction

Suppose \[{\text{aA + bB}} \to {\text{cC + dD}}\]

Then \[{\text{rate = k}}{\left[ {\text{A}} \right]^{{\alpha }}}{\left[ {\text{B}} \right]^{{\beta }}}\]

Here instead of using complex reaction we use elementary reaction which gets solved in one step. 

22. Which of the following statements are applicable to a balanced chemical equation of an elementary reaction?

A. Order is the same as molecularity.

B. Order is less than molecularity.

C. Order is greater than molecularity.

D. Molecularity can never be zero.

Ans: Correct options: A and D 

Elementary reaction: It is a reaction that occurs in a single step.

Here we must understand about the Order and Molecularity.

Molecularity of a reaction = number of reacting species (collide to bring a chemical reaction).

Discussing about the Order, Rate law is used in Order and how do we equate shall be seen in the next step

\[{\text{rate = k}}{\left[ {\text{A}} \right]^{{\alpha }}}{\left[ {\text{B}} \right]^{{\beta }}}\]For a balanced chemical equation of an elementary reaction Order and Molecularity is same and can never be 0. 

23. In any unimolecular reaction ______________.

A. only one reacting species is involved in the rate determining step. 

B. the order and the molecularity of the slowest step are equal to one.

C. the molecularity of the reaction is one and order is zero.

D. both molecularity and order of the reaction are one.

Ans: Correct options: A and B

Unimolecular reaction: Unimolecular means relating to a single molecular reaction that describes decomposition of a single reactant.

If product \[{\text{A}} \to {\text{(B)}}\]

\[{\text{rate = k}}\left[ {\text{A}} \right]\]

Example \[{\text{N}}{{\text{a}}_{\text{2}}}{{\text{O}}_{\text{4}}}{\text{(g)}} \to {\text{2N}}{{\text{o}}_{\text{2}}}{\text{(g)}}\]

Order = 1

Molecularity = 1

The slowest step is the rate determining which determines the Order and Molecularity.

24. For a complex reaction ______________.

A. order of overall reaction is same as molecularity of the slowest step.

B. order of overall reaction is less than the molecularity of the slowest step. 

C. order of overall reaction is greater than molecularity of the slowest step.

D. molecularity of the slowest step is never zero or non-integer

Ans: Correct options: A and D

A complex reaction is one that does not happen in a single step.

The total number of molecules involved in the slowest step of the reaction determines the overall reaction rate.

25. At high pressure the following reaction is zero order

\[{\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g)}}\xrightarrow[{{\text{platinumcatalyst}}}]{{{\text{1130K}}}}{{\text{N}}_{\text{2}}}{\text{(g) + 3}}{{\text{H}}_{\text{2}}}{\text{(g)}}\]

Which of the following options are correct for this reaction? 

A. Rate of reaction = Rate constant

B. Rate of the reaction depends on concentration of ammonia.

C. Rate of decomposition of ammonia will remain constant until ammonia disappears completely. 

D. Further increase in pressure will change the rate of reaction.

Ans: Correct options: A, C and D

The pressure in this reaction is extremely high, and it becomes independent of the ammonia concentration. The metal surface becomes saturated with gas molecules when the rate of reaction=Rate constant. The rate of a zero-order reaction is independent of the concentration of reactants in the reaction.

26. During decomposition of an activated complex

A. energy is always released 

B. energy is always absorbed

C. energy does not change

D. reactants may be formed

Ans: Correct options: A and D

Activation Energy is the amount of energy released when reactant molecules collide and form an activated complex. When energy is released, the complex decomposes into a product.

27. According to Maxwell Boltzmann distribution of energy, __________. 

A. the fraction of molecules with most probable kinetic energy decreases at higher temperatures.

B. the fraction of molecules with most probable kinetic energy increases at higher temperatures.

C. most probable kinetic energy increases at higher temperatures.

D. most probable kinetic energy decreases at higher temperatures.

Ans: Correct options: A and C

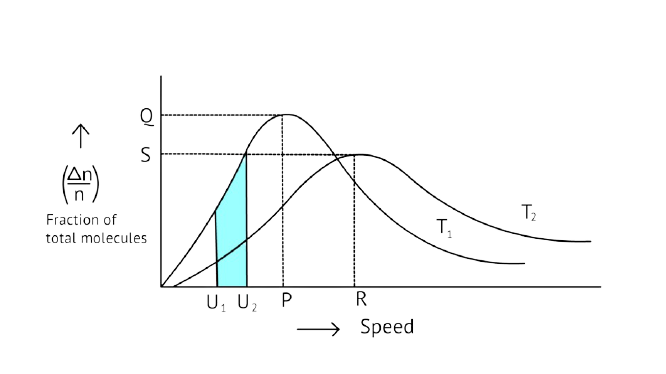
The Maxwell Boltzmann distribution, often known as the Gibbs distribution, is a measure that expresses the likelihood of a system being in each state as a function of the energy of that state.

Look at the graph.

\[{{\text{T}}_{\text{2}}}{\text{ > }}{{\text{T}}_{\text{1}}}\]

The fraction of molecules falls as the temperature rises because the area under the curve shrinks.

28. In the graph showing Maxwell Boltzmann distribution of energy, ___________. 

A. area under the curve must not change with increase in temperature.

B. area under the curve increases with increase in temperature.

C. area under the curve decreases with increase in temperature. 

D. with increase in temperature curve broadens and shifts to the right-hand side.

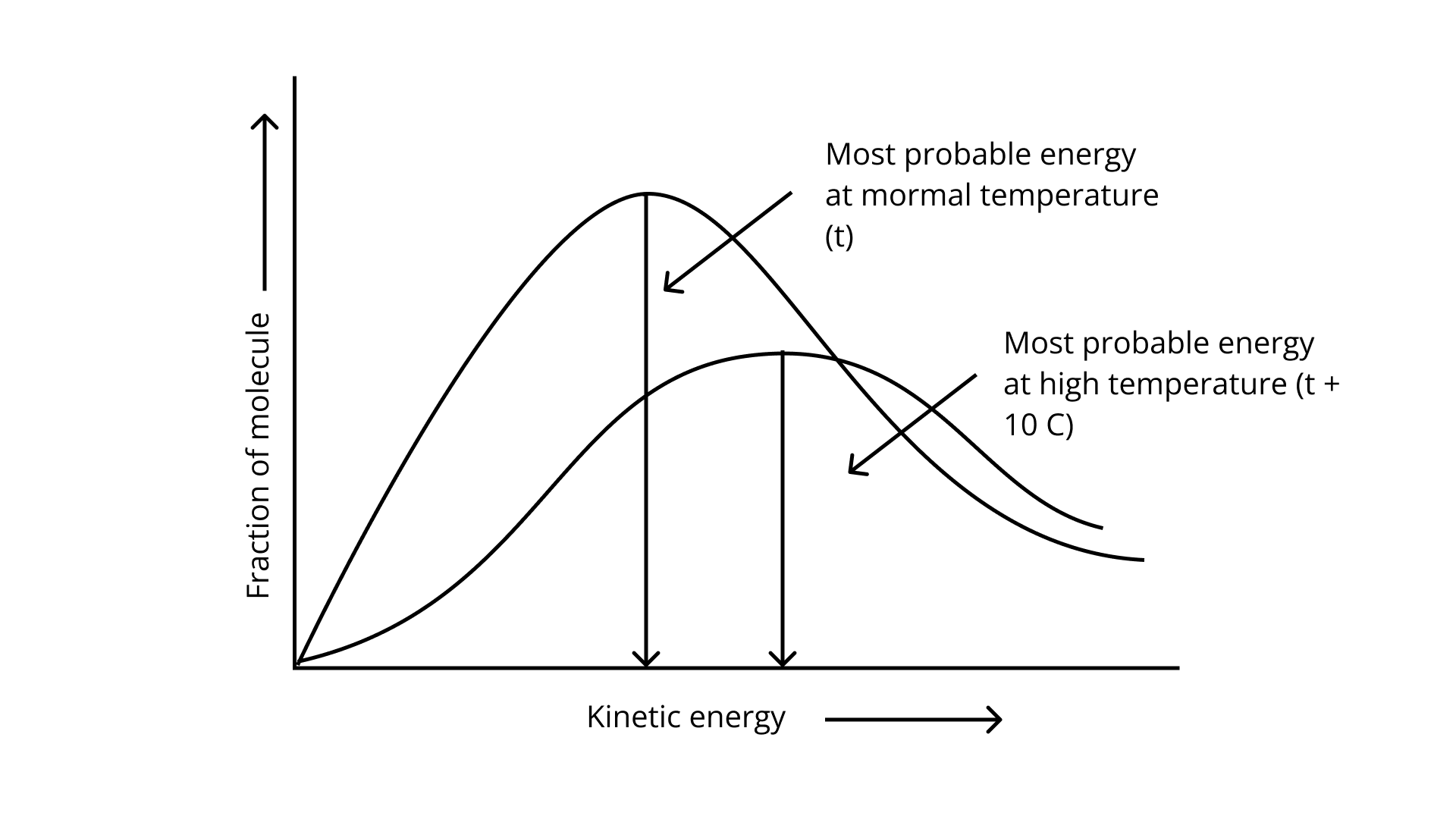
Ans: Correct options: A and D

According to the graph, the area under the cure must not vary as the temperature rises.\[{{\text{T}}_{\text{2}}}{\text{ > }}{{\text{T}}_{\text{1}}}\]

The energy level of \[{{\text{T}}_{\text{2}}}\] is higher than \[{{\text{T}}_{\text{1}}}\].

29.  Which of the following statements are in accordance with the Arrhenius equation?

A. Rate of a reaction increases with increase in temperature.

B. Rate of a reaction increases with decrease in activation energy.

C. Rate constant decreases exponentially with increase in temperature.

D. Rate of reaction decreases with decrease in activation energy.

Ans: Correct options: A and B

Arrhenius equation \[{\text{k = Ae - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\]

When the temperature rises, \[\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\] values fall and \[ - \dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\] rises.

As a result, \[{\text{e - }}\dfrac{{{{\text{E}}_{\text{a}}}}}{{{\text{RT}}}}\] increases, and it is certain that \[{\text{k}}\] and  \[{\text{T}}\] increases as well. As a result, Option A is proven.

Catalyst increases the rate of reaction by lowering the activation energy. Thus option B is also correct. 

30. Mark the incorrect statements.

A. Catalyst provides an alternative pathway to reaction mechanism.

B. Catalyst raises the activation energy.

C. Catalyst lowers the activation energy.

D. Catalyst alters enthalpy change of the reaction

Ans: Correct options: B, C and D

Catalysts reduce the activation energy of a process and give an alternate path by reducing or raising the activation energy between reactants and products, altering the reaction's enthalpy change. As a result, B, C, and D statements are the proper responses.

31. Which of the following graphs is correct for a zero-order reaction? 

A.

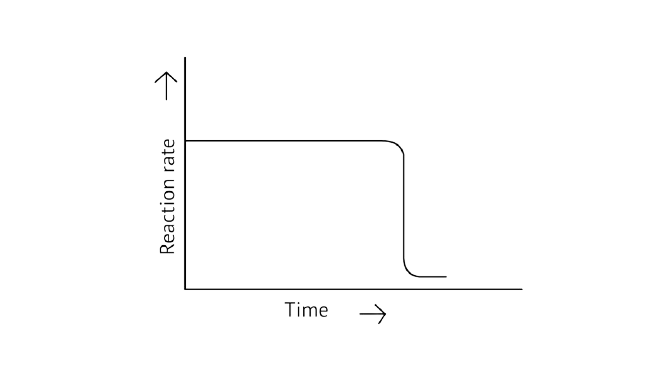
B.

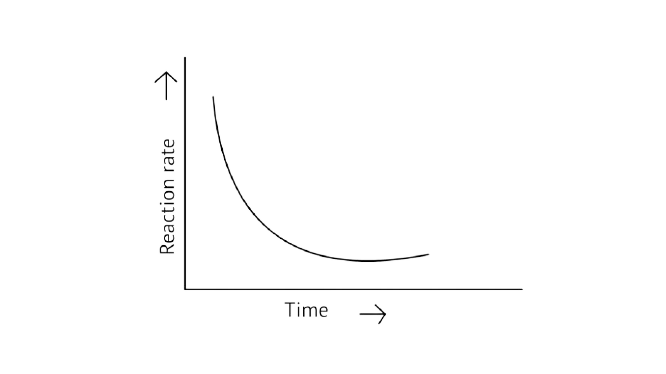
C.

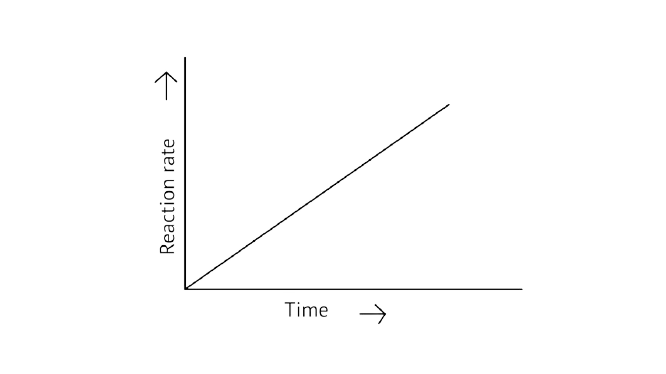
D.

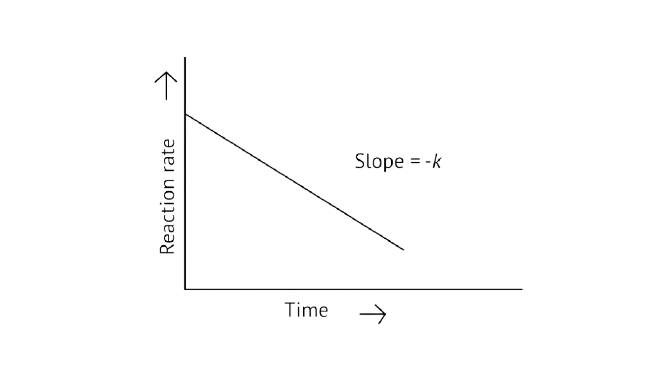
Ans: Correct options: A and D

A Zero order reaction = \[\left[ {\text{R}} \right]{\text{ = }}\left( {{\text{ - k}}} \right){\text{t + }}{\left[ {\text{R}} \right]_{\text{0}}}\]

\[{\text{y = (m }\times{ x) + c}}\]

\[{\text{x = t(time)}}\]

\[{\text{y = }}\left[ {\text{R}} \right]{\text{concentration}}\]

\[{\text{Slope(m) =  - k}}\]

\[{\text{Intercept(c) = }}{\left[ {\text{R}} \right]_{\text{0}}}\]

\[\dfrac{{\left[ {\text{R}} \right]{\text{ - }}{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\text{t}}}{\text{ =  - k}}\]

\[\dfrac{{\left[ {\text{R}} \right]{\text{ - }}{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\text{t}}}{\text{ =  - k}}{{\text{t}}^{\text{o}}}\]

\[{\text{Rate} \alpha }{{\text{t}}^{\text{0}}}\]

32. Which of the following graphs is correct for a first order reaction?

A.

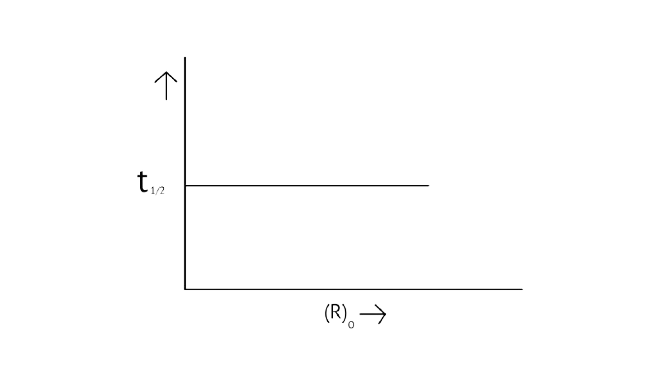
B.

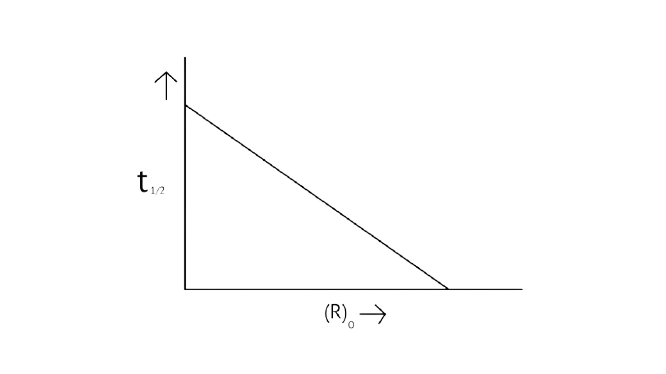
C.

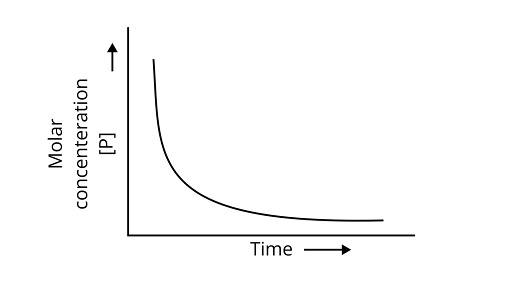
D.

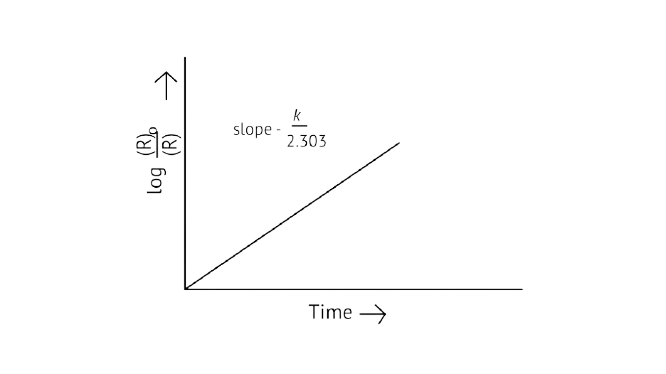
Ans: Correct options: A and D

The pace of a reaction that is directly proportional to the concentration of the reacting substance is known as a first order reaction. 

A first-order reaction's kinetic equation \[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\left[ {\text{R}} \right]}}\]

The Y axis represents concentration, whereas the X axis represents time.

\[{\text{log = }}\dfrac{{{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\left[ {\text{R}} \right]}}{\text{ = }}\dfrac{{{\text{kt}}}}{{{\text{2}}{\text{.303}}}}\]

\[\left[ {{\text{log = }}\dfrac{{{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\left[ {\text{R}} \right]}}} \right]{\text{ = }}\left[ {\dfrac{{{\text{kt}}}}{{{\text{2}}{\text{.303}}}}} \right]\left( {\text{t}} \right)\]

\[{\text{y  =  mn}}\]

\[{\text{k = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{t}}}{\text{log}}\dfrac{{\text{a}}}{{{\text{a - x}}}}\]

\[{\text{t = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{k}}}{\text{log}}\dfrac{{\text{a}}}{{{\text{a - x}}}}\]

\[{\text{x = a - }}\dfrac{{\text{a}}}{{\text{2}}}\]

\[{\text{x = }}\dfrac{{\text{a}}}{{\text{2}}}\]

\[{{\text{t}}_{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{ = }}\dfrac{{{\text{2}}{\text{.303}}}}{{\text{k}}}{\text{log}}\dfrac{{\text{a}}}{{{\text{a - }}\dfrac{{\text{a}}}{{\text{2}}}}}\]

\[\dfrac{{{\text{2}}{\text{.303}}}}{{\text{k}}}{\text{log2}}\]

\[{{\text{t}}_{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{ = }}\dfrac{{{\text{0}}{\text{.693}}}}{{\text{k}}}\]

III. Short Answer Type

33. State a condition under which a bimolecular reaction is kinetically first order reaction.

Ans:  A bimolecular reaction occurs when two particles collide. The product of the concentrations of both elements determines the rate of reaction. If one of the reactants is taken in substantial excess in such a way that its concentration seldom changes, a bimolecular reaction can be kinetically first order.

34. Write the rate equation for the \[{\text{2A + B}} \to {\text{C}}\] if the order of the reaction is zero.

Ans: Given: Order of the reaction = 0

We know that a zero order reaction is a chemical reaction that occurs regardless of the reactant's concentration.

The rate law of \[{\text{2A + B}} \to {\text{C}}\] is

\[{\text{r = k}}{\left[ {\text{A}} \right]^{\text{0}}}{\left[ {\text{B}} \right]^{\text{0}}}\]

For a zero- order reaction

\[{\text{r = k}}\]

35. How can you determine the rate law of the following reaction?  

\[{\text{2NO(g) + }}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{2N}}{{\text{O}}_{\text{2}}}{\text{(g)}}\]

Ans: Experimentally, the reaction's rate law can be calculated.

Step 1

\[{\text{2NO(g) + }}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{2N}}{{\text{O}}_{\text{2}}}{\text{(g)}}\]

\[{{\text{O}}_{\text{2}}}{\text{(g)}}\] is taken in excess

x molecules of \[{\text{NO}}\] number reacting with excess of \[{{\text{O}}_{\text{2}}}\]

\[{\text{r = k}}{\left[ {{\text{NO}}} \right]^{\text{x}}}\]

Step 2

\[{\text{2NO(g) + }}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{2N}}{{\text{O}}_{\text{2}}}{\text{(g)}}\]

When \[{\text{2No(g)}}\]is taken in excess

Y molecules of \[{{\text{O}}_{\text{2}}}\] reacting with excess of \[\left[ {{\text{NO}}} \right]\]

\[{\text{rate = k}}{\left[ {{{\text{O}}_{\text{2}}}} \right]^{\text{y}}}\]

\[{\text{rate = k}}{\left[ {{\text{NO}}} \right]^{\text{x}}}{\left[ {{\text{NO}}} \right]^{\text{y}}}\]

36. For which type of reactions, order and molecularity have the same value?

Ans: The order and molecularity of elementary reactions are the same. As a result of a single collision between two molecules or ions, a complicated process occurs. A reaction mechanism is a set of elementary reactions.

37. In a reaction if the concentration of reactant A is tripled, the rate of reaction becomes twenty-seven times. What is the order of the reaction?

Ans: Let order of reaction be = \[{\text{n}}\]

\[{\text{rate = k}}{\left[ {\text{A}} \right]^{\text{n}}}\]--------(i)

\[{\text{27r = k}}{\left[ {{\text{3A}}} \right]^{\text{n}}}\]--------(ii)

Divide (ii) by (i)

\[\dfrac{{{\text{27r}}}}{{\text{r}}}{\text{ = }}\dfrac{{{\text{k}}{{\left[ {{\text{3A}}} \right]}^{\text{n}}}}}{{{\text{k}}{{\left[ {\text{A}} \right]}^{\text{n}}}}}\]

\[{{\text{3}}^{\text{n}}}{\text{ = 27}}\]

\[{\text{n = 3}}\]

38. Derive an expression to calculate time required for completion of zero order reaction.

Ans: The concentration of the reactants does not change with time in a zero- order reaction, and the rate of concentration remains constant.

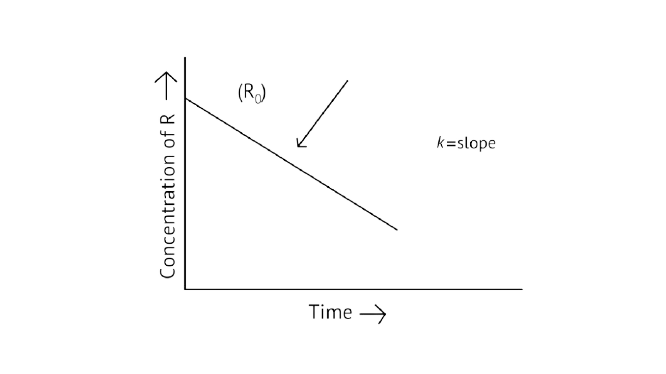
\[{\text{R = }}{\left[ {\text{R}} \right]_{\text{0}}}{\text{ - Kt}}\]

\[{\text{Kt = }}{\left[ {\text{R}} \right]_{\text{0}}}\]

\[{\text{t = }}\dfrac{{{{\left[ {\text{R}} \right]}_{\text{0}}}}}{{\text{K}}}\]

39. For a\[{\text{A + B}} \to {\text{Products}}\], the rate law is\[{\text{Rate = k}}\left[ {\text{A}} \right]{\left[ {\text{B}} \right]^{{\text{3/2}}}}\].Can the reaction be an elementary reaction? Explain.

Ans: The number of ions or atoms that collide to react is known as molecularity in an elementary reaction. The order of reaction about \[{\text{B}}\] should be 1 if this is an elementary reaction, however the rate law given is. \[\dfrac{3}{2}\]

40. For a certain reaction a large fraction of molecules has energy more than the threshold energy, yet the rate of reaction is very slow. Why?

Ans: When the Threshold energy is less than the energy of the molecules and the orientation of the molecules is proper for the effective collision, the reaction happens. As a result, the reaction is slow, and the number of effective collisions is reduced.

41. For a zero-order reaction will the molecularity be equal to zero? Explain

Ans: The concentration of the reactants does not change with time in a zero -order reaction, and the rate of concentration remains constant. The molecularity of a reaction cannot be 0 because it indicates the number of reactants involved.

42. For a general reaction \[{\text{A + B}} \to {\text{C}}\], plot of concentration of \[{\text{A}}\] vs time is given in Fig. 4.3. Answer the following based on this graph.

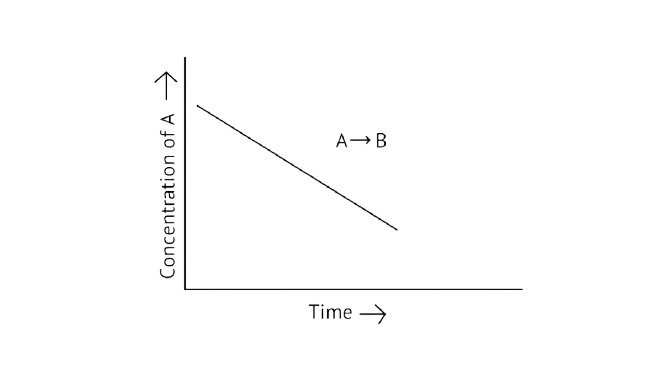
A. What is the order of the reaction? 

Ans: The reaction has a zero order. The concentration of the reactants does not change with time in a zero order reaction, and the rate of concentration remains constant.

B. What is the slope of the curve?

Ans: Slope of the curve is \[{\text{ - k}}\]

C. What are the units of rate constant?

Ans: The rate constant's units are \[{\text{mol}}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}\]

43. The reaction between \[{{\text{H}}_{\text{2}}}{\text{(g)}}\] and \[{{\text{O}}_{\text{2}}}{\text{(g)}}\] is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.

Ans: The reaction's activation energy is relatively high at room temperature and not readily available, the reaction is highly viable. \[{{\text{H}}_{\text{2}}}{\text{(g)}}\] and \[{{\text{O}}_{\text{2}}}{\text{(g)}}\]bond break and clash, allowing particles to pass across the energy barrier.

\[{\text{2}}{{\text{H}}_{\text{2}}}{\text{ + }}{{\text{O}}_{\text{2}}} \to {\text{2}}{{\text{H}}_{\text{2}}}{\text{O}}\]

Because of the large activation energy, the water molecule does not form in this equation.

44. Why does the rate of a reaction increase with rise in temperature?

Ans: The energy possessed by the reacting species increases as the temperature rises, the pace of a reaction increases. This raises the temperature and raises the average kinetic energy of the reactant molecules.

45.  Oxygen is available in plenty in the air, yet fuels do not burn by themselves at room temperature. Explain

Ans: The activation energy for fuel combustion reactions is very large, and because every substance or element requires an ignition temperature to function and excite to a higher temperature, oxygen in air does not combust to fire.

46. Why is the probability of reaction with molecularity higher than three very rare?

Ans: The chance of more than three molecules meeting at the same time is extremely minimal, reactions with molecularity more than three are extremely rare. Simultaneous collisions decrease as the number grows, the probability is very low, and more than three reactions with molecularity are uncommon.

47. Why does the rate of any reaction generally decrease during the reaction?

Ans: The pace of any reaction is determined by the concentration of the reactants, the rate of any reaction generally declines during the reaction. As the reaction progresses, the reactant concentration declines, and the product concentration rises.

48. Thermodynamic feasibility of the reaction alone cannot decide the rate of the reaction. Explain with the help of one example

Ans: Thermodynamic feasibility is determined by \[{\text{}\Delta{ G}}\] factors. So, while the conversion of diamond to graphite is thermodynamically viable, the reaction is sluggish and has a high activation energy.

Gibb's free energy is \[{\text{}\Delta{ G}}\].

\[{\text{}\Delta{ G =   -  RT l nk}}\]

\[{\text{}\Delta{ }}{{\text{G}}_{{\text{P,T}}}}{\text{ > O}}\]at constant pressure and temperature should be negative or less than 0.

For example, Diamond to be converted to Graphite

\[{\text{}\Delta{ G =   -  ve}}\]

It is theoretically conceivable, but the rate is extremely slow, and the activation energy is extremely high. The energy required to transform diamond to graphite is insufficient.

49. Why in the redox titration of \[{\text{KMn}}{{\text{O}}_{\text{4}}}\] vs oxalic acid, we heat oxalic acid solution before starting the titration?

Ans: At room temperature, the redox titration of  \[{\text{KMn}}{{\text{O}}_{\text{4}}}\]vs oxalic acid is exceedingly slow; nevertheless, as the temperature rises, so does the rate of reaction. At a temperature of ${\text{5}}{{\text{0}}^{\text{0}}}{\text{c}}{\text{.}}$, \[{\text{KMn}}{{\text{O}}_{\text{4}}}\] is acidified with dil \[{{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}\] and interacts with oxalic acid.

50. Why can’t molecularity of any reaction be equal to zero?

Ans: The number of molecules of the reactants involved in an elementary reaction is referred to as the molecularity of the reaction. For this, a single molecule with a minimum molecularity of one is required, and it cannot be zero.

51. Why molecularity is applicable only for elementary reactions and order is applicable for elementary as well as complex reactions?

Ans: Simple reactions occur in a single stage, whereas complicated reactions occur in multiple steps. Each phase in a multi-step process has its own molecularity, which is not added together. There is no molecularity in complex reactions. The sequence of a complex reaction is decided by the slowest step. As a result, it can be used for both simple and complex processes.

52. Why can we not determine the order of a reaction by taking into consideration the balanced chemical equation?

Ans: Incorrect order results from a balanced chemical equation. \[{\text{KCl}}{{\text{O}}_{\text{3}}}{\text{ + 6FeS}}{{\text{O}}_{\text{4}}}{\text{ + 3}}{{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}} \to {\text{KCl + 3}}{{\text{H}}_{\text{2}}}{\text{O + 3F}}{{\text{e}}_{\text{2}}}{{\text{(S}}{{\text{O}}_{\text{4}}}{\text{)}}_{\text{3}}}\]

This reaction is complex and occurs in several steps. The order is determined by the slowest in the reactions.

IV. Matching Type

Note. In the following questions match the items of Column I with appropriate item given in Column II.

53. Match the graph given in Column I with the order of reaction given in Column II. More than one item in Column I may link to the same item of Column II.

Column I	Column II
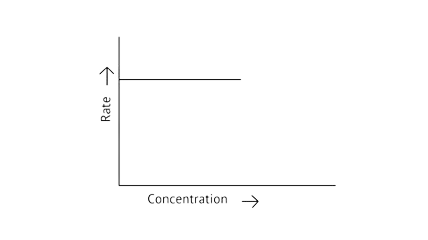
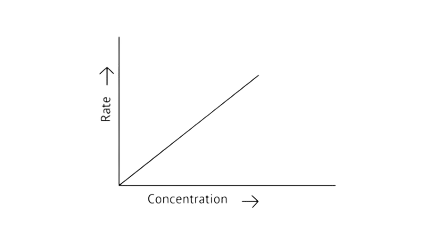
	1st order
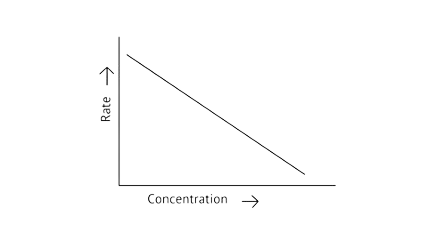
	Zero order

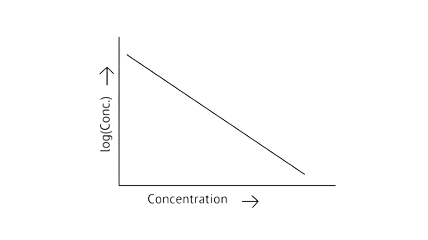
Ans:

Column I	Column II
	1st order
	Zero order
	Zero order
	1st order

A zero-order reaction is one in which the reactant concentrations do not change over time and the rate of concentration remains constant.

A first-order reaction is one in which the rate of the reaction is linearly proportional to the concentration of only one ingredient. In other terms, a first-order reaction is a chemical reaction whose rate is determined by changes in only one of the reactants' concentration.

54. Match the statements given in Column I and Column II

Ans: 

A catalyst can influence the rate of a process by lowering the activation energy.

When it comes to molecularity, there can't be a fraction or a zero.

The second half life of a first order reaction is the same as the first.

Activation energy refers to the percentage of molecules with an energy equal to or greater than activation energy.

Correct orientation is not always present when it comes to energetically favourable activities.

Because the area under the Maxwell Boltzmann curve is constant, the total probability is one.

55. Match the items of Column I and Column II.

Ans:

The rate of conversion in diamond is normally imperceptible.

Long-term rate at a moment's notice

The average rate is only for a short time.

56. Match the items of Column I and Column II.

Ans:

The rate rule was discovered experimentally and can be used to predict the reaction rate and reactant concentrations.

The rate constant is the proportionality constant that describes the relationship between the molar concentration of the reactants and the rate of a chemical reaction.

The rate constant (k) of a reaction is proportional to its temperature, i.e., for a given reaction at a given temperature, the rate constant (k) is constant.

The order of a reaction is a quantity that has been empirically determined. As a result, the reaction rate is mostly determined by the slowest phase of the reaction. In the event of a complicated reaction, the stoichiometric coefficients of this rate-determining step match to the reaction order.

V. Assertion and Reason Type

Note. In the following questions a statement of assertion followed by a statement of reason is given. 

Choose the correct answer out of the following choices.

A. Both assertion and reason are correct, and the reason is correct  of assertion.

B. Both assertion and reason are correct, but reason does not explain assertion.

C. Assertion is correct, but reason is incorrect

D. Both assertion and reason are incorrect.

E. Assertion is incorrect, but reason is correct.

57. Assertion: Order of the reaction can be zero or fractional.

Reason: We cannot determine order from balanced chemical equation.

Ans: Correct option: B

Both assertion and reason are valid, but reason does not explain assertion because the order of reaction can be zero or even fractional because the order of reaction is proportional to the total of the power of the reactants.

58. Assertion: Order and molecularity are same.

Reason: Order is determined experimentally, and molecularity is the sum of the stoichiometric coefficient of rate determining elementary step.

Ans: Correct option: E

The order and molecularity may or may not be the same, assertion is false, but reason is right. The sum of the power of the reactants is the order of reaction, which may be easily determined. The total of the stoichiometric coefficient of the rate-determining elementary step determines molecularity.

59. Assertion: The enthalpy of reaction remains constant in the presence of a catalyst. 

Reason: A catalyst participating in the reaction, forms different activated complex and lowers down the activation energy but the difference in energy of reactant and product remains the same. 

Ans: Correct option: A

Both the assertion and the reason are valid, and the reason is a correct  of the assertion since the enthalpy of reaction is the difference between the total enthalpy of the reactants and products in the presence of a catalyst.

60. Assertion: All collision of reactant molecules leads to product formation.

Reason: Only those collisions in which molecules have correct orientation and sufficient kinetic energy lead to compound formation. 

Ans: Correct option: E

The claim is erroneous, but the reason is right, because the correct assertion is that effective collision leads to the production of a product, and the reason states that the conditions of collision theory must be met for the reaction to be completed.

61. Assertion: Rate constants determined from Arrhenius equation are accurate for simple as well as complex molecules.

Reason: Reactant molecules undergo chemical change irrespective of their orientation during collision.

Ans: Correct option: C

The assertion is valid, but the reasoning is erroneous because Arrhenius equation rate constants are accurate for both simple and complex molecules with suitable orientation during effective collision and sufficient kinetic energy to cause chemical change.

VI. Long Answer Type

62. All energetically effective collisions do not result in a chemical change. Explain with the help of an example.

Ans: The reaction rate in collision theory is determined by two factors: energy and orientation factor. Certain reactions can be highly exothermic and energetically favoured, meaning the reactants have enough activation energy to collide effectively. However, they do not proceed at a fixed temperature, which is why the reactant molecules are not orientated properly during collisions, resulting in atoms of reactant molecules combining to produce products that do not face each other.

64. What happens to most probable kinetic energy and the energy of activation with increase in temperature?

Ans:

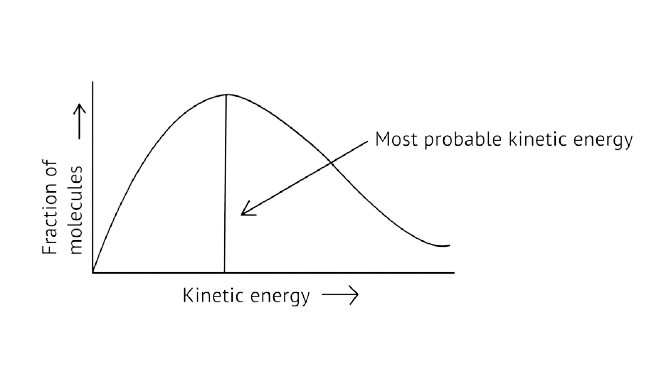
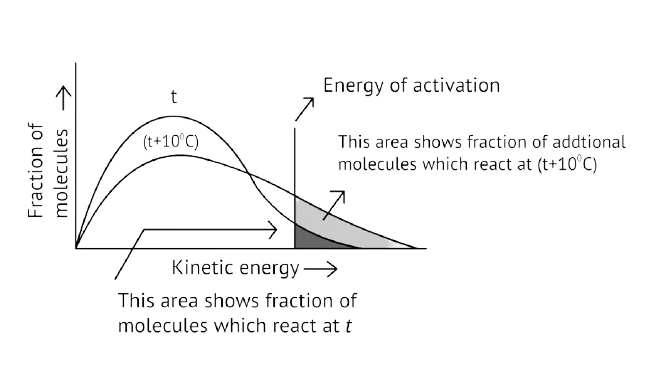
As  illustrated in the graph, as the temperature rises, the peak pushes ahead, increasing probable kinetic energy while decreasing the number of molecules utilizing it, resulting in a faster rate of reaction.

64. Describe how the enthalpy of reaction remains unchanged when a catalyst is used in the reaction.

Ans: Catalyst action is a complicated concept. A catalyst aids in the formation of temporary bonds during a chemical reaction. The objective of a catalyst is to lowers the activation energy. A catalyst is a substance that increases the rate of a reaction without itself undergoing any permanent chemical change. The action of the catalyst can be explained by intermediate complex theory. According to this theory, a catalyst participates in a chemical reaction by forming temporary bonds with the reactants resulting in an intermediate complex. This has transitory existence and decomposes to yield products and the catalyst.

A small amount of the catalyst can catalyst a large number of reactants. A catalyst does not alter Gibbs energy, ΔG of a reaction. The difference in energy between reactants and products is constant.

It is also found that a catalyst does not change the equilibrium constant of a reaction rather, it helps in attaining the equilibrium faster, that is, it catalyses the forward as well as the backward reactions to the same extent so that the equilibrium state remains the same enthalpy of reaction means the difference in energy between reactant and product it will also remain unchanged. 

65. Explain the difference between instantaneous rate of a reaction and average rate of a reaction.

Ans: Average rate depends upon the change in concentration of reactants or products and the time taken for that change to occur. However, the average rate cannot be used to predict the rate of reaction at a particular instance as it would be constant for the time interval for which it is calculated. 

So, to express the rate at a particular moment of time we determine the instantaneous rate. Itis obtained when we consider the average rate at the smallest time interval say dt (i.e. when △t approaches zero). 

66. With the help of an example explain what is meant by pseudo first order reaction.

Ans: Tell us about the pseudo-first-order reaction. It's the reaction with the highest true rate law, yet it behaves like a first order reaction, but it's more specifically a second order reaction.

As an example, consider the hydrolysis of an ester.

\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{COO}}{{\text{C}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{5}}}{\text{ + }}{{\text{H}}_{\text{2}}}{\text{O}} \to {\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH + }}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{OH}}\]

\[{\text{rate = k}}\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{COO}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}} \right]\left[ {{{\text{H}}_{\text{2}}}{\text{O}}} \right]\]…(constant)

${{\text{k}}_{\text{1}}}\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{COO}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}} \right]$

${\text{k = k}}\left[ {{{\text{H}}_{\text{2}}}{\text{O}}} \right]$ 

Class 12 Chemistry Chemical Kinetics Vedantu’s NCERT Exemplar Solutions

In Chemistry Chapter 4 Chemical Kinetics, students learn about the average and instantaneous rate of a reaction, rate of a reaction in terms of change in concentration of either of the reactants or products with time, elementary and complex reactions, the molecularity and order of a reaction, meaning of rate constant, the dependence of the rate of reactions on concentration, temperature, and catalyst, derive integrated rate equations (for zero and first-order reactions), determining the rate constants for zeroth and first-order reactions, and meaning of Collision Theory . 

The study of Chemical Kinetics helps students to understand how Chemical reactions occur and factors controlling the rate of a Chemical reaction. All these questions can be answered by the study of Chemical Kinetics. Kinetics studies also help students to determine the conditions by which the reaction rates can be altered such as concentration, temperature, pressure, and catalyst. 

The NCERT Exemplar solutions provided by Vedantu’s subject experts help students to understand all the concepts covered in Chemistry Chapter 4. The solutions are easy to grasp and help students prepare well for their final Exams. The solutions are prepared by Chemistry teachers of Vedantu that help students get tuned in with all the concepts covered in Chemical Kinetics. 

The Class 12 Chemical Kinetics Chapter includes various crucial topics for students important for the board Examinations and also for competitive Exams like JEE Mains and NEET. Students are advised to solve all the NCERT exemplar problems. NCERT Example problems should be solved thoroughly along with the previous year’s Chemistry question papers and sample papers to understand the final Exam pattern and score good marks.