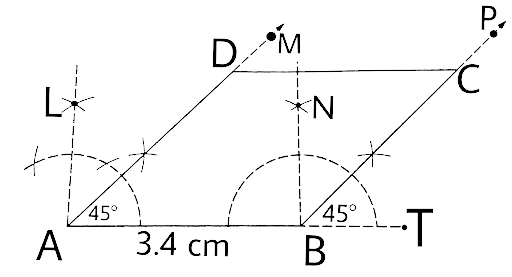
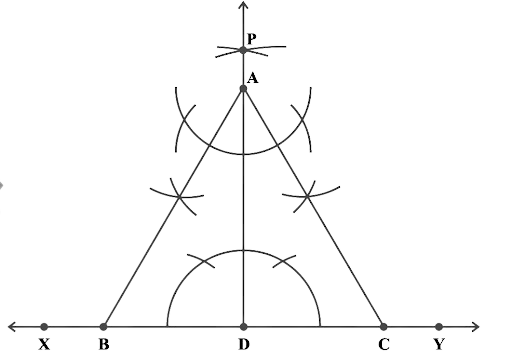
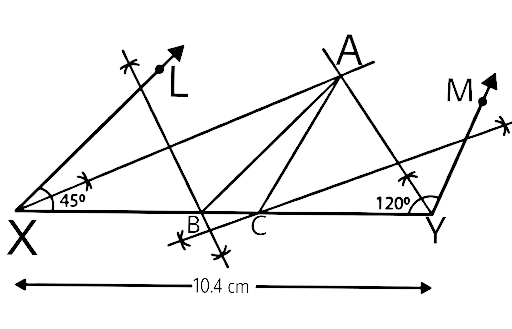
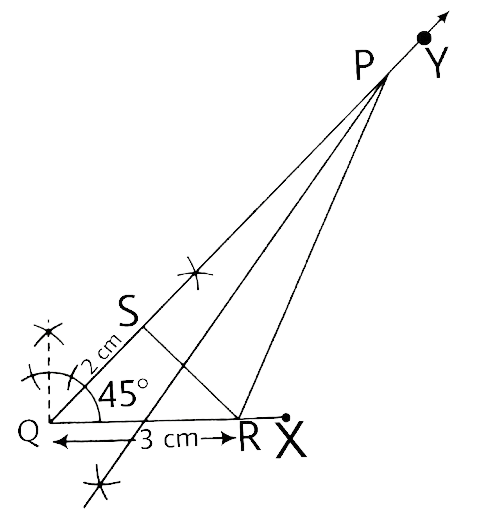
Constructions Book Solutions by Vedantu
FAQs on NCERT Exemplar for Class 9 Math Chapter 11 - Constructions (Book Solutions)
1. How do I practice NCERT Class 9 Math Chapter 11?
You can refer to NCERT Exemplar for Class 9 Math Chapter 11- Constructions on Vedantu.com. Constructions exercise questions with solutions will assist you in revising the complete syllabus and scoring higher marks in your respective examinations. Students must practice them on a regular basis so as to get better at the subject. The solutions have been well explained in the book and so all doubts will be automatically clarified in the process of solving those questions. The explanations for each are written in a lucid manner.
2. What are Geometrical Constructions?
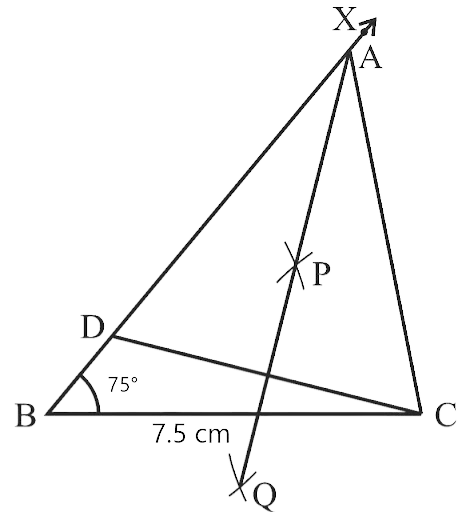
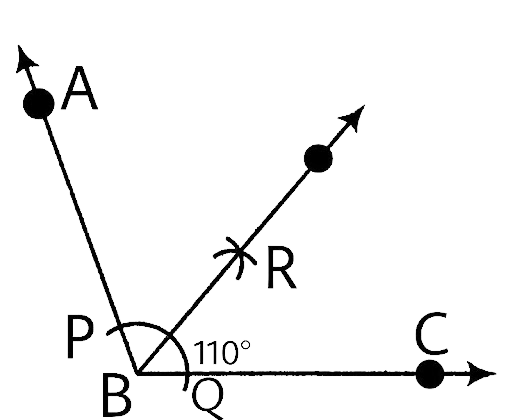
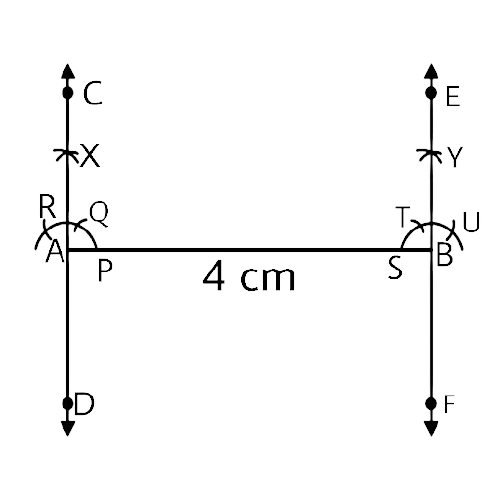
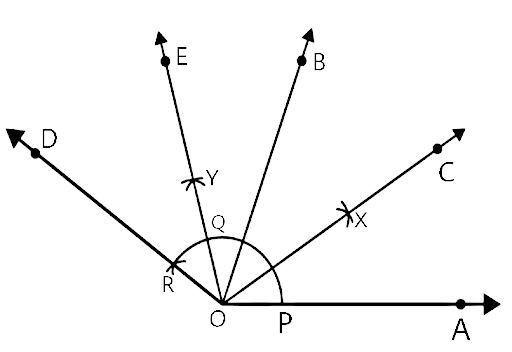
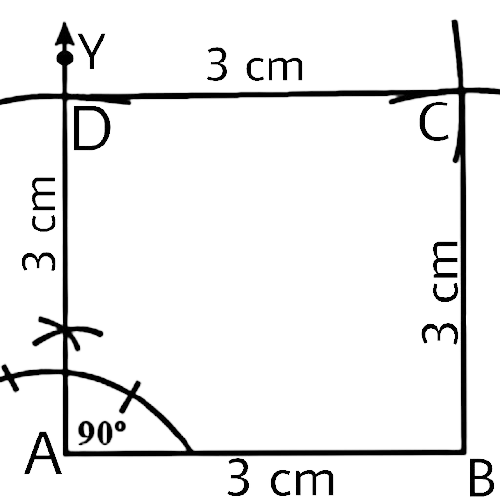
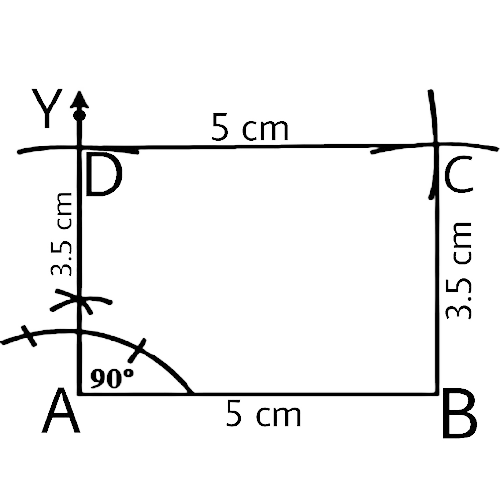
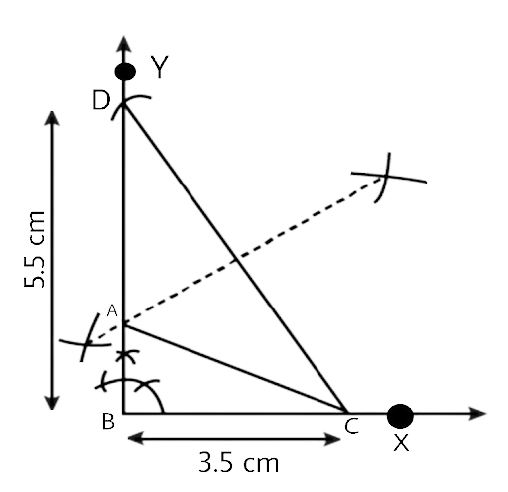
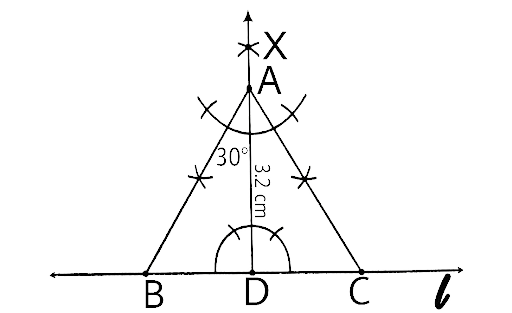
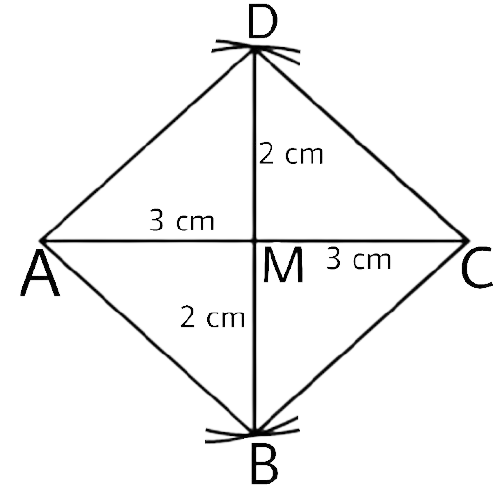
In geometrical constructions, drawings are done through the help of an non graduated ruler known as a straight edge along with a compass. A graduated scale and a protractor could also be used if the measurements are needed. NCERT Exemplar for Class 9 Math Chapter 1- Constructions on Vedantu The concepts have been explained well along with the necessary diagrams and examples. It is an important chapter to grasp as it forms the base of Geometry which will help students in the successive grades.
3. Can I download the NCERT Exemplar for Class 9 Math Chapter 1- Constructions in the form of a PDF?
Yes, very much so. All students can download the NCERT Exemplar for Class 9 Math Chapter 1- Constructions in the form of a PDF which is absolutely free and available on Vedantu’s portal.
On the Vedantu site, select ‘Study Material’ and then under CBSE, choose CBSE revision notes. You can either go through the notes online or download them in a PDF format and then study as per your convenience. Either way, the notes prove to be quite handy.
4. How can I construct triangles properly?
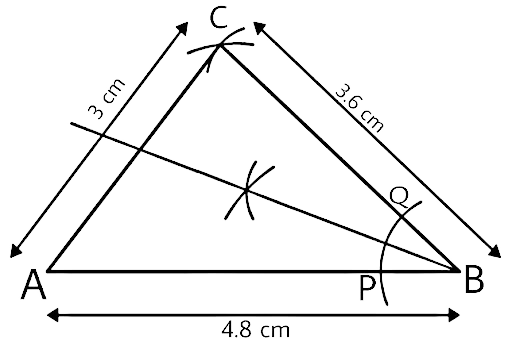
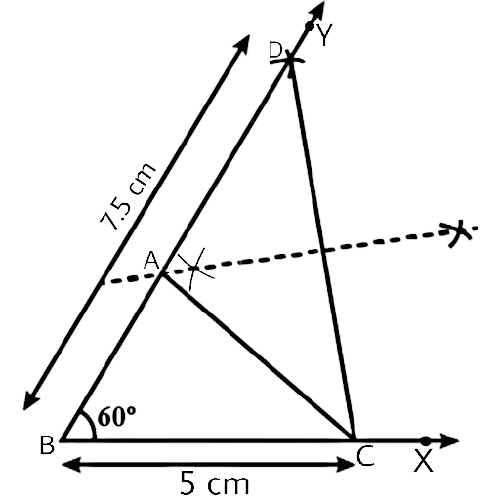
Measurement of all three elements of any triangle is needed so as to develop a triangle. A protractor, a pair of compasses, and a ruler are needed to create them. Three properties are required, namely, SAS (Side, Angle, Side), ASA (Angle, Side, Angle), and SSS (Side, Side, Side)
Ensure that the construction lines are not wiped out as these things ensure that the triangle has been properly constructed. You can even refer to NCERT Exemplar for Class 9 Math Chapter 1- Constructions for a better understanding.
5. Where can I find relevant material for Class 9 Math Chapter 1- Constructions?
You can find proper explanations and matter for Class 9 Math Chapter – Constructions on Vedantu.com. Ans: You can find proper explanations and matter for Class 9 Math Chapter – Constructions on Vedantu.com. The book has all the solutions for the students to practice from and do well in examinations. The questions have been designed keeping the NCERT curriculum in mind and so, you will find similar questions in the examinations that you might take. Consistent reading and revision will make sure that you ace those tests.