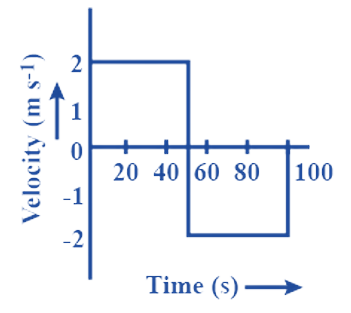
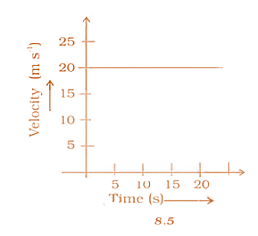
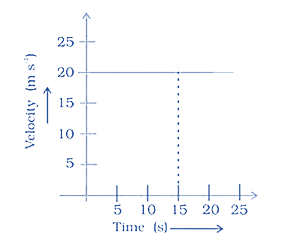
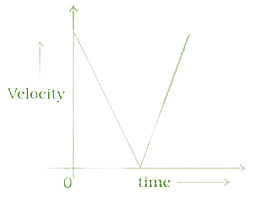
NCERT Exemplar for Class 9 Science Chapter 8 - Motion (Book Solutions)

Exercise

Multiple Choice Questions

1. A particle is moving in a circular path of radius r. The displacement after half a circle would be:

(a) Zero

(b) \[\pi r\]

(c) \[2r\]

(d) \[2\pi r\]

Ans: (c) \[2r\]

Explanation: The particle will be diametrically opposite its origin after half of a circle. As a result, displacement equals diameter.

2. A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,

(a) \[\dfrac{u}{g}\]

(b) \[\dfrac{{{u^2}}}{{2g}}\]

(c) \[\dfrac{{{u^2}}}{g}\]

(d) \[\dfrac{u}{{2g}}\]

Ans: (b) \[\dfrac{{{u^2}}}{{2g}}\]

3. The numerical ratio of displacement to distance for a moving object is

(a) always less than 1

(b) always equal to 1

(c) always more than 1

(d) equal or less than 1

Ans: (d) equal or less than 1

Explanation: Displacement can be the same as or less than distance, but it can never exceed it.

4. If the displacement of an object is proportional to the square of time, then the object moves with

(a) uniform velocity

(b) uniform acceleration

(c) increasing acceleration

(d) decreasing acceleration

Ans: (b) uniform acceleration

Explanation: Acceleration is measured in distance per square second, whereas velocity is measured in distance per second. As a result, uniform acceleration is the correct solution.

5. From the given v – t graph (Fig. 8.1), it can be inferred that the object is

(a) in uniform motion

(b) at rest

(c) in non-uniform motion

(d) moving with uniform acceleration

Ans: (a) in uniform motion

Explanation: On the x-axis, a straight horizontal line above zero indicates homogeneous motion.

6. Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of \[10m{s^{ - 1}}\]. It implies that the boy is

(a) at rest

(b) moving with no acceleration

(c) in accelerated motion

(d) moving with uniform velocity

Ans: (c) in accelerated motion

Explanation: A boy on a merry-go-round is spinning in a circle. Acceleration motion is exemplified by circular motion.

7. Area under a v – t graph represents a physical quantity which has the unit

(a) \[{m^2}\]

(b) \[m\]

(c) \[{m^3}\]

(d) \[m{s^{ - 1}}\]

Ans: (b) m

Explanation: Displacement is represented by the specified area. The metre is the unit of measurement for displacement.

8. Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs is shown in Fig. 8.2. Choose the correct statement

(a)  Car A is faster than car D.

(b) Car B is the slowest.

(c) Car D is faster than car C.

(d) Car C is the slowest.

Ans: (b) Car B is the slowest.

Explanation: The graph for car B reaches the lowest height (on the x-axis) in the shortest amount of time. As a result, it is the slowest vehicle.

9. Which of the following figures (Fig. 8.3) represents the uniform motion of a moving object correctly?

(a)

(b)

(c)

(d)

Ans: (a)

Explanation: As evidenced by the upward slanting straight line, distance is growing at a consistent rate. As a result, this graph depicts uniform motion.

10. Slope of a velocity-time graph gives

(a) the distance

(b) the displacement

(c) the acceleration

(d) the speed

Ans: (c) the acceleration

Explanation: The reason behind this is that acceleration is equal to the product of velocity and time. 

11. In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?

(a) If the car is moving on a straight road

(b) If the car is moving in a circular path

(c) The pendulum is moving to and fro

(d) The earth is revolving around the Sun

Ans: (a) If the car is moving on a straight road

Explanation: In all other classes, displacement can be less than distance.

Short Answer Questions

12. The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero? Justify your answer.

Ans: The fact that the displacement is zero does not imply that the distance is also zero. When a moving object returns to its original position, the displacement can be 0 (zero). Displacement is either equal to or less than distance but the distance traveled is always more than zero.

13. How will the equations of motion for an object moving with a uniform velocity change?

Ans: When the object is moving with a uniform velocity, then \[V = \mu \] and\[a = 0\]. Under such conditions, an equation for distance would be:

\[s = ut\] and \[{V^2} - {\mu ^2} = 0\]

14. A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement–time graph is shown in Fig. 8.4. Plot a velocity-time graph for the same.

Ans: For the initial \[50\] seconds, velocity is \[2{\text{ }}m/s\].Then, velocity drops of 0; as depicted by the vertical line in the graph.

For the next 50 seconds, velocity is taken in negative because displacement is becoming zero.

15. A car starts from rest and moves along the x-axis with constant acceleration \[5m{s^{ - 2}}\] for \[8\] seconds. If it then continues with constant velocity, what distance will the car cover in \[12\] seconds since it started from the rest?

Ans: The distance travelled in first \[8s\], \[{x_1} = 0 + \dfrac{1}{2}(5){(8)^2} = 160m\]

At this point the velocity \[v = u + at = 0 + (5 \times 8) = 40m{s^{ - 1}}\]

Therefore, the distance covered in last four seconds, \[{x_2} = (40 \times 4)m = 160m\]

Thus, the total distance \[x = {x_1} + {x_2} = (160 + 160)m = 320m\]

16. A motorcyclist drives from A to B with a uniform speed of \[32km{h^{ - 1}}\] and returns back with a speed of\[20km{h^{ - 1}}\]. Find its average speed.

Ans: Let \[AB = {x_2}\] So \[{t_1} = \dfrac{x}{{30}}\] and \[{t_2} = \dfrac{x}{{20}}\]

Total time \[ = {t_1} + {t_2} = \dfrac{{5x}}{{60}}h\]

Average speed for entire journey\[ = \dfrac{{{\text{Total distance}}}}{{{\text{Total time}}}} = \dfrac{{2x}}{{\dfrac{{5x}}{{60}}}} = 24km{h^{ - 1}}\]

17. The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find 

(i) itsacceleration 

Ans: (i) Since the velocity is constant, acceleration is equal to 0.

(ii) its velocity 

Ans: (ii) Reading the graph, velocity \[ = 20m{s^{ - 1}}\]

(iii) the distance covered by the cyclist in 15 seconds.

Ans: (iii) Distance covered in 15 seconds, \[s = u \times t = 20 \times 15 = 300m\]

18. Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height.

Ans: The maximum velocity of a stone is when it is flung upward. When the stone starts gaining height, the velocity begins to fall. Velocity becomes 0, Once the stone has attained the maximum height. After that, the stone begins to fall down. At this point, velocity begins to rise. When the stone hits the ground, its velocity reaches its peak.

Long Answer Questions

19. An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height of 100 m. What is the difference in their heights after 2 s if both the objects drop with the same accelerations? How does the difference in heights vary with time?

Ans: Initial difference in height \[ = {\text{ }}\left( {150--100} \right){\text{ }}m{\text{ }} = {\text{ }}50{\text{ }}m\]

Distance travelled by first body in \[2s = {h_1} = 0 + \dfrac{1}{2}g{(2)^2} = 2g\]

Distance travelled by another body in \[2s = {h_2} = 0 + \dfrac{1}{2}g{(2)^2} = 2g\]

After \[2s\], height at which the first body will be \[ = {h_1}' = 150 - 2g\]

After \[2s\], height at which the second body will be \[ = {h_2}' = 100 - 2g\]

Thus, after \[2s\], 

difference in height \[ = {\text{ }}150{\text{ }}-{\text{ }}2{\text{ }}g{\text{ }}-{\text{ }}\left( {100{\text{ }}-{\text{ }}2g} \right) = {\text{ }}150{\text{ }} - 2g - 100 + 2g\]

\[ = {\text{ }}50{\text{ }}m{\text{ }} = \]initial difference in height

Thus,  it can be concluded that the difference in height does not vary with time.

20. An object starting from rest travels 20 m in first 2 s and 160 m in next 4 s. What will be the velocity after 7 s from the start?

Ans: \[{s_1} = ut + \dfrac{1}{2}a{t^2}\] 

or \[20 = 0 + \dfrac{1}{2}a{(2)^2}\] 

or \[a = 10m{s^{ - 1}}\]

\[v{\text{ }} = {\text{ }}u{\text{ }} + {\text{ }}at{\text{ }} = {\text{ }}0{\text{ }} + {\text{ }}\left( {10{\text{ }} \times {\text{ }}2} \right){\text{ }} = {\text{ }}20m{s^{ - 1}}\]

\[{s_2} = 160 = ut' + \dfrac{1}{2}a'{(t')^2} = (20 \times 4) + (\dfrac{1}{2}a' \times 16) \Rightarrow a' = 10m{s^{ - 2}}\]

Since acceleration is the same, we have \[v'{\text{ }} = {\text{ }}0{\text{ }} + {\text{ }}\left( {10{\text{ }}x{\text{ }}7} \right){\text{ }} = {\text{ }}70m{s^{ - 1}}\]

21. Using following data, draw time-displacement graph for a moving object:

Use this graph to find average velocity for first 4 s, for next 4 s and for last 6 s.

Ans:

Average velocity for first 4s.

Average velocity\[ = \dfrac{{{\text{change in displacement}}}}{{{\text{Total time taken}}}}\]

\[v = \dfrac{{4 - 0}}{{4 - 0}} = \dfrac{4}{4} = 1m{s^{ - 1}}\]

For next 4s, 

\[v = \dfrac{{4 - 4}}{{8 - 4}} = \dfrac{0}{4} = 0m{s^{ - 1}}\]

(or as x remains the same from 4 to 8 seconds, velocity is zero)

For last 6s, \[v = \dfrac{{0 - 6}}{{16 - 10}} =  - 1m{s^{ - 1}}\]

22. An electron moving with a velocity of \[5 \times {10^4}m{s^{ - 1}}\] enters into a uniform electric field and acquires a uniform acceleration of \[{10^4}m{s^{ - 2}}\]in the direction of its initial motion.

(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.

Ans: Given initial velocity, \[u{\text{ }} = {\text{ }}5{\text{ }}x{\text{ }}{10^4}m{s^{ - 1}}\]

And acceleration, \[a = {10^4}m{s^{ - 2}}\]

(i) final velocity \[ = v{\text{ }} = {\text{ }}2u{\text{ }} = {\text{ }}2{\text{ }} \times {\text{ }}5{\text{ }} \times {\text{ }}{10^4}m{s^{ - 1}}{\text{ }} = {\text{ }}10{\text{ }} \times {\text{ }}{10^4}m{s^{ - 1}}\]

To find t, use \[v{\text{ }} = {\text{ }}u{\text{ }} + {\text{ }}at\]

Or \[t = \dfrac{{v - u}}{a}\]

\[\left( {\dfrac{{10 \times {{10}^4} - 5 \times {{10}^4}}}{{{{10}^4}}}} \right) = \dfrac{{5 \times {{10}^4}}}{{{{10}^4}}} = 5s\]

(ii) How much distance the electron would cover in this time?

Ans: Using \[s = ut + \dfrac{1}{2}a{t^2}\]

\[ = \left( {5 \times {{10}^4}} \right) \times 5 + \dfrac{1}{2}\left( {{{10}^4}} \right) \times {(5)^2} = 25 \times 10 + \dfrac{{25}}{2} \times {10^4} = 37.5 \times {10^4}m\]

23. Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds.

Ans:Using the equation of motion \[s = ut + \dfrac{1}{2}a{t^2}\]

Distance travelled in 5s \[s = u \times 5 + \dfrac{1}{2}a{t^2}\]

Or \[s = 5u + \dfrac{{25}}{2}a -  -  -  -  -  -  - (i)\]

Similarly, distance travelled in 4s, \[s' = 4u + \dfrac{{16}}{2}a -  -  -  -  -  -  - (ii)\]

Distance travelled in the interval between 4th and 5th second \[(s - s') = (u + \dfrac{9}{2}a)m\]

24. Two stones are thrown vertically upwards simultaneously with their initial velocities \[{u_1}\] and \[{u_2}\] respectively. Prove that the heights reached by them would be in the ratio of \[u_1^2:u_2^2\] (Assume upward acceleration is -g and downward acceleration to be +g.

Ans: We know for upward motion, \[{v^2} = {u^2} - 2gh\] or \[h = \dfrac{{{u^2} - {v^2}}}{{2g}}\]

But at highest point v = 0

Therefore, \[h = \dfrac{{{u^2}}}{{2g}}\]

For first ball, \[{h_1} = \dfrac{{{u_1}^2}}{{2g}}\]

And for second ball, \[{h_2} = \dfrac{{{u_2}^2}}{{2g}}\]

Thus, \[\dfrac{{{h_1}}}{{{h_2}}} = \dfrac{{\dfrac{{{u_1}^2}}{{2g}}}}{{\dfrac{{{u_2}^2}}{{2g}}}}\] or \[{h_1}:{h_2} = {u_1}^2:{u_2}^2\]

Chapter 8 of Class 9th NCERT deals with the concepts of motion. It is one of the most essential chapters of the Class 9th Science syllabus. Motion is generally described as the change of position and it is referred to in terms of both distance and displacement. Some of the key points that are covered in this chapter are:

• The change of position of an object is defined in reference to a point known as origin.

• This change of position can be either uniform or non-uniform on the basis of velocity.

• The motion of an object in a straight line is referred to as uniform motion. The velocity is constant, in uniform motion, that is, the object covers equal distance in equal intervals of time.

• In case of non-uniform motion, the velocity of the object keeps on changing, as the object does not cover the same distance in equal intervals of time.

• These motions are depicted in the form of graphs.

• If the object moves in a circular path with uniform speed, then the motion is known as uniform circular motion.

• The velocity of an object is defined as the displacement of the object per unit time.

• The speed of the object is defined as the speed of the object per unit time.

• The acceleration of the object is described as the change in velocity per unit time.

• Motions are also represented in the form of graphs.

• Graphs are the most accessible method to display basic information about different events of motion.

• The popular graphs that are drawn to interpret the motion of an object are the distance-time graph and velocity-time graph.

• There are three main equations used to describe the motion of an object moving at uniform acceleration. These three equations are:

1. v = u + at

2. S = ut + \[\frac {1}{2}\] at²

3. v²= u² + 2aS

where,

u = initial velocity

v = final velocity

a = acceleration

t = time

S = distance

Expectations from Class 9th Chapter 8 of Science NCERT

The motion chapter of science NCERT is constructed in such a way that it gives an insight to the students about the fundamentals of motion. The important sections that are covered in this chapter of Class 9th Science NCERT are:

• Basics of motion

• Relation among kinematic quantities

• Fundamentals of graphs

• Calculation of acceleration in a speed-time graph

• Calculation of distance or displacement in the speed-time graph

• Importance of slope and area by evaluating relations in kinematical variables.