NCERT Exemplar for Class 9 Math - Number Systems - Free PDF Download
FAQs on NCERT Exemplar for Class 9 Math Chapter 1 - Number Systems (Book Solutions)
1. What are the Important points to be noted in NCERT Math Exemplar Problems and Solutions for Class 9 Chapter 1?
If a number ‘r’ can be written as p/q, then, at that point, ‘r’ is known as a rational number, where p and q ought to be whole numbers and q isn't equivalent to 0.
Assuming a number s can't be written as p/q, where p and q ought to be integers and q isn't equivalent to 0.
When we gather every objective and irrational number, then, it makes up the group of real numbers.
These are some of the important points of NCERT Math Exemplar Problems and Solutions for Class 9.
2. How many sets of questions are there in each exercise of NCERT Math Exemplar Problems and Solutions for Class 9 Chapter 1?
The questions of this chapter comprise all significant subjects of the section like kinds of numbers, number line, ration, and irrational numbers, their properties, and so forth.
Practice 1 of the section comprises 21 problems which are for the multiple-choice questions and cover every one of the subjects of the section.
Exercise 2 of chapter 1 consists of 4 questions.
Exercise 3 has around 14 questions
Exercise 4 of the chapter consists of 7 questions that are mostly long-form answers.
3. What are the Benefits of NCERT Exemplar Class 9 Math Solutions Chapter 1 by Vedantu?
The benefits are as follows:
At Vedantu our essential target is your assistance and development in education. The NCERT Exemplar answers for Class 9 Math section 1 given by us are refreshed now and again to give you the best and reliable content.
We have numerous phenomenal examples of overcoming adversity of students who have scored so well in view of the stage given by us. The best thing about Vedantu is that the review material is given at liberation from cost and is available whenever, anyplace.
4. How does Vedantu help Class 9 students to score good marks?
At Vedantu, we submit vast assistance, assets, and direction for the students. Each of these solution books given by us goes about as a source of a prospective book for a student which further assists them with examining in a successful way. Revisions are made simple, and answers are rearranged. Download the solutions today and capitalize on them straight away. You can also find answers for other subjects for Class 9 NCERT. Go directly to the Vedantu site to start your excursion towards simple and proficient learning. Great learning!
5. What topics are covered in NCERT Exemplar Class 9 Math Chapter 1?
The topics are as follows:
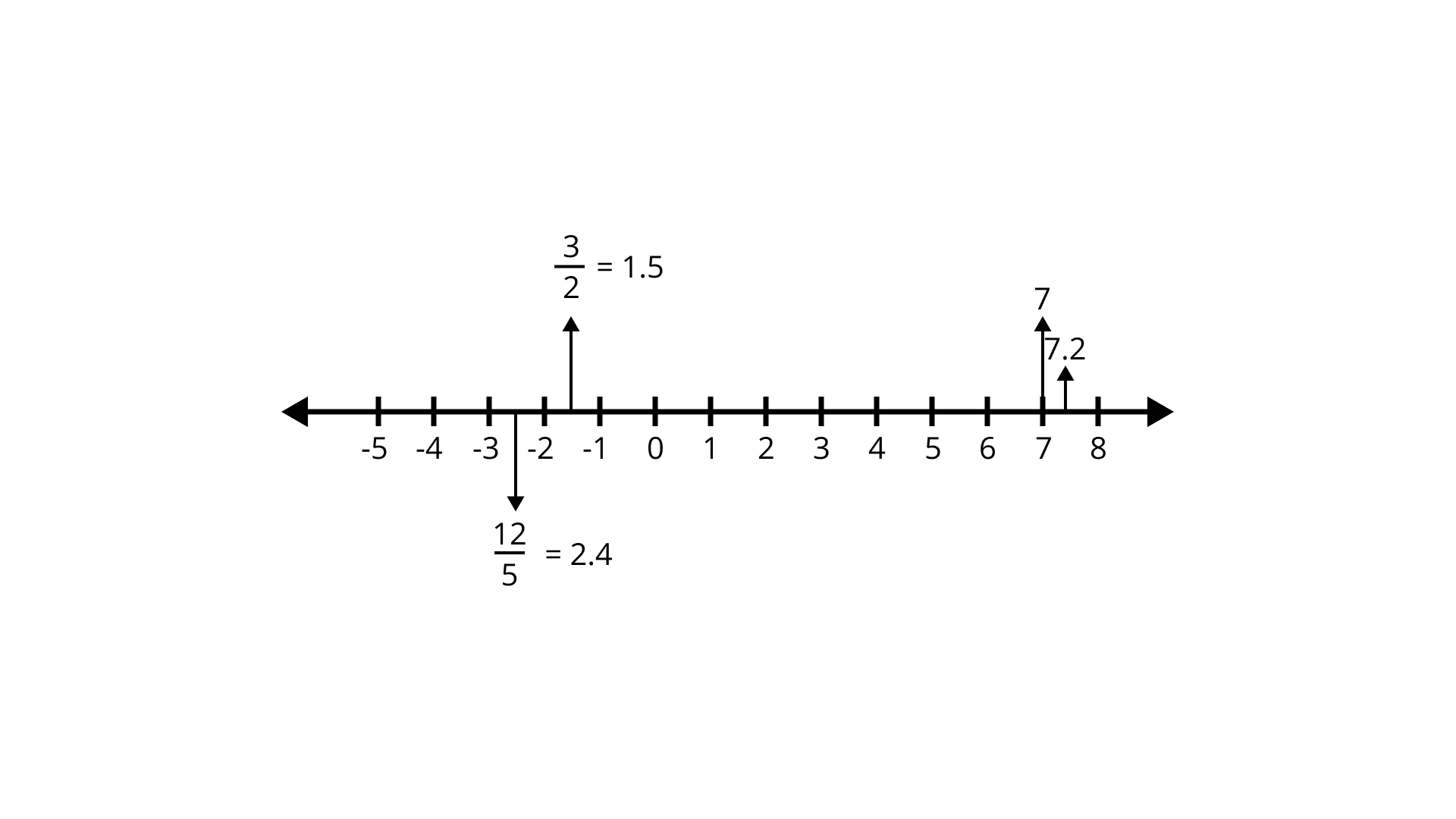
Rational Numbers and Irrational numbers
Finding rational numbers
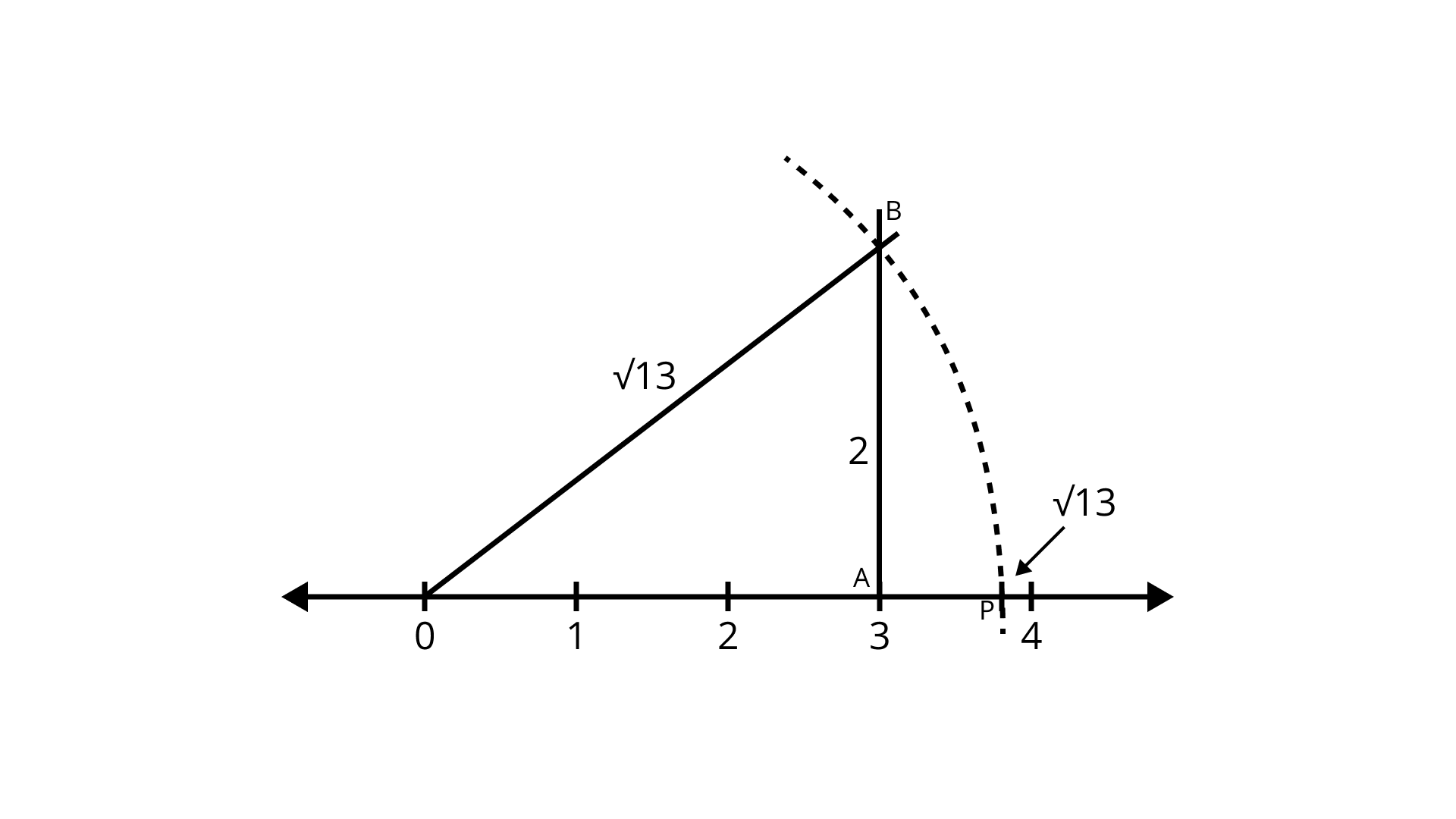
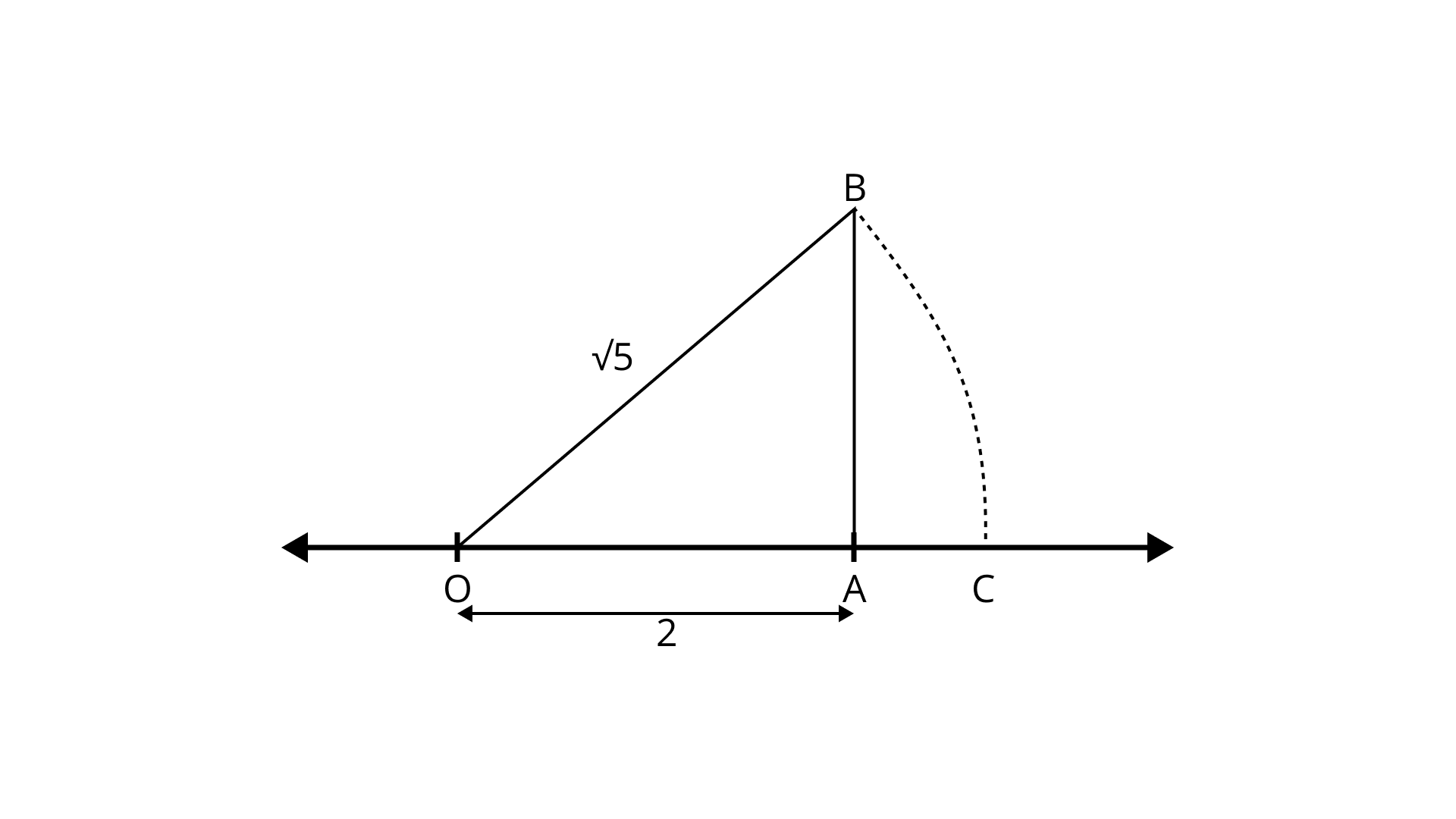
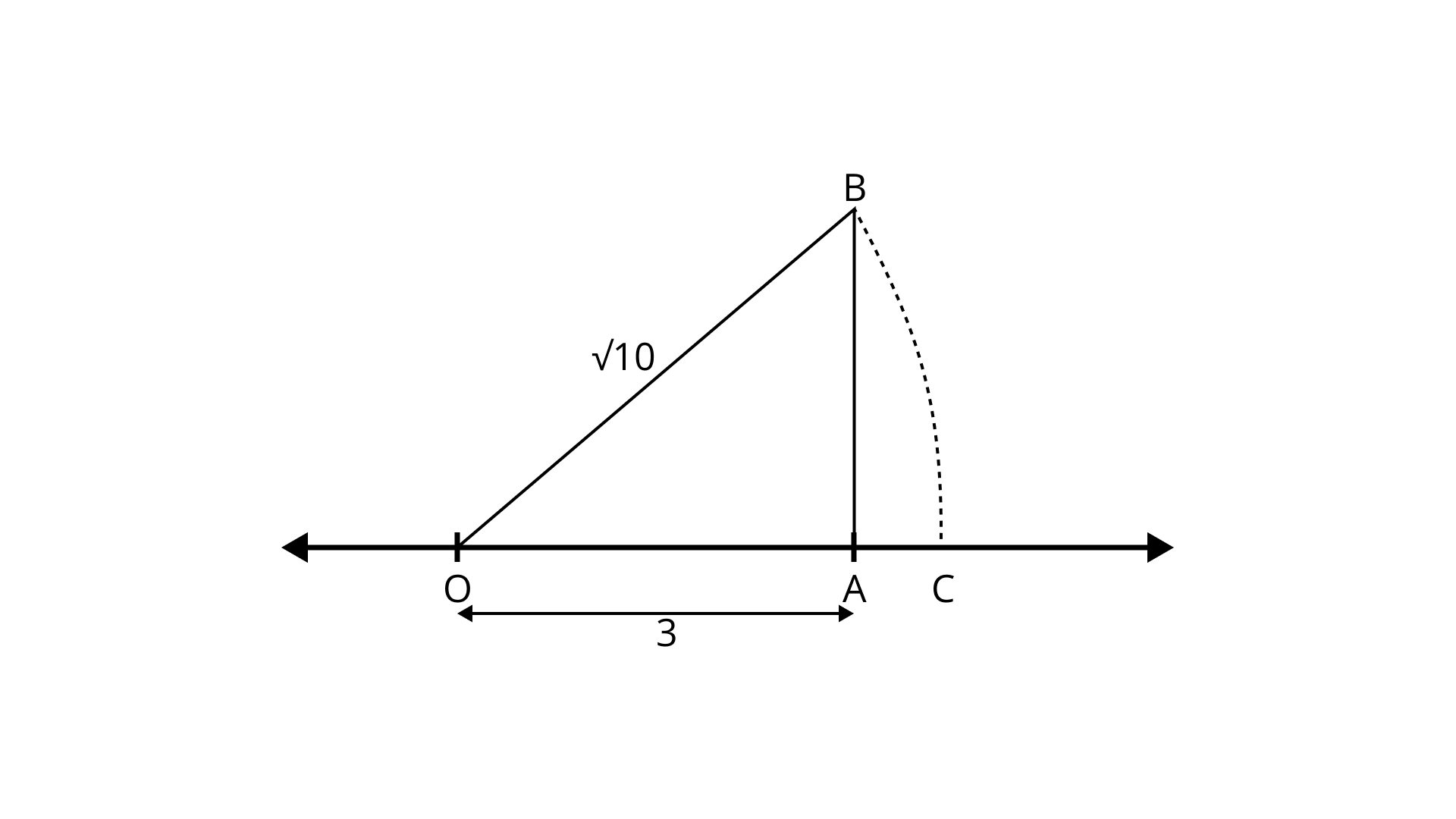
Locating irrational numbers
Real Numbers and Their Decimal Expansions
Finding irrational numbers
Real numbers
Rationalizing the denominator
Laws of Exponents for Real Numbers
To work with simple learning and assist students with understanding the ideas examined in Chapter 1, free NCERT Exemplars are given here which can be additionally downloaded as a PDF. Students can utilize these materials as a kind of perspective device for concentrating just as rehearsing sums.