NCERT Exemplar for Class 9 Maths - Areas of Parallelograms and Triangles - Free PDF Download

Multiple Choice Questions

Write the correct answer:

Sample Question 1: The area of the figure formed by joining the mid- points of the adjacent sides of a rhombus with diagonals 12 cm and 16 cm is 

(A). 48 $\text{c}{{\text{m}}^{\text{2}}}$         

(B). 64 $\text{c}{{\text{m}}^{\text{2}}}$             

(C). 96 $c{{m}^{2}}$            

(D). 192 $c{{m}^{2}}$ 

Ans: The correct answer is option (A).

Let ABCD is a rhombus and points F, G, H and E are the midpoints of the sides AB, BC, CD and AD respectively. 

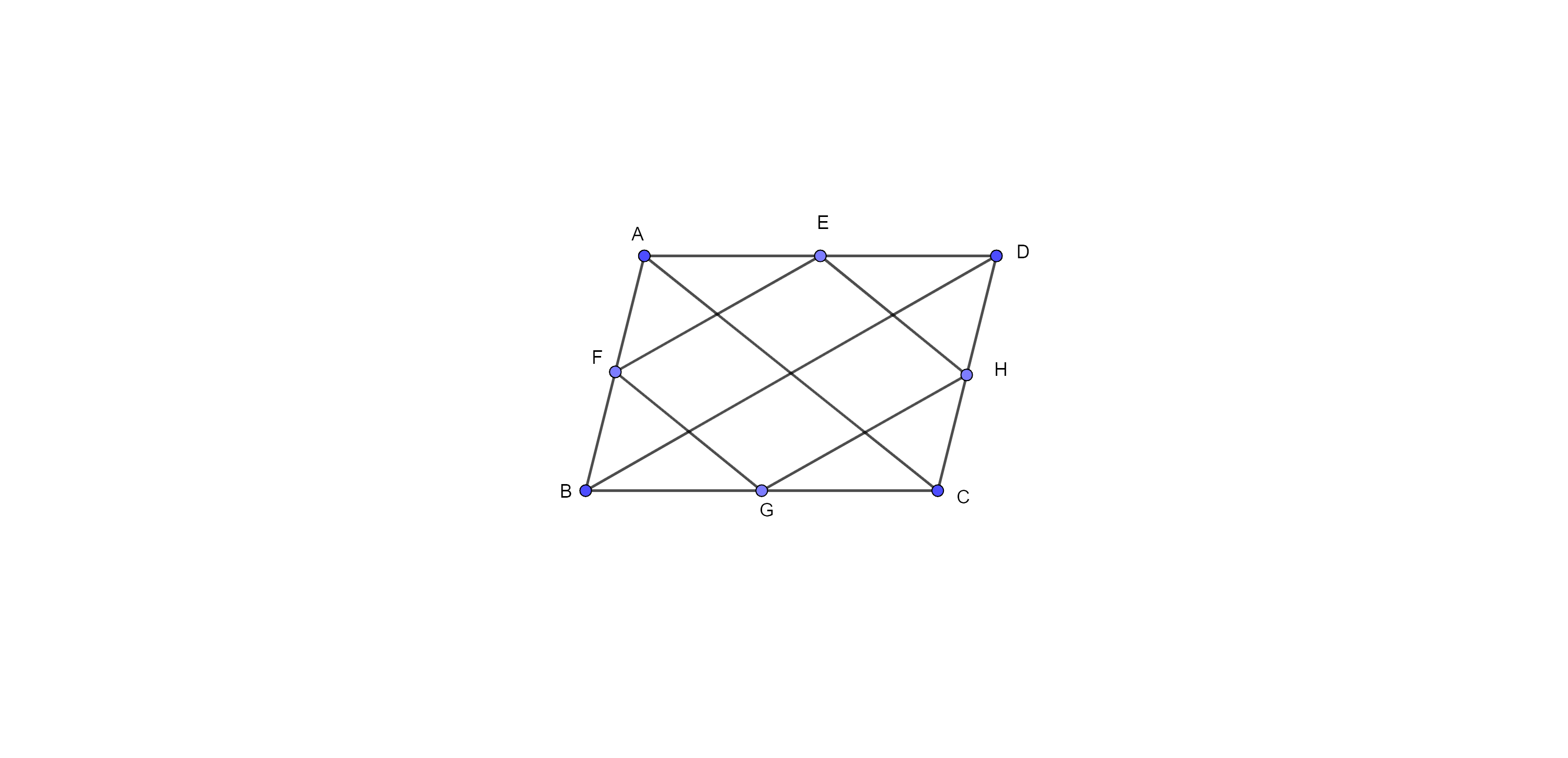
Now, join the midpoints of adjacent sides, 

Diagonals (BD) = 16 cm and diagonal (AC) = 12 cm

Now, in $\Delta BAD,$ F is the midpoint of AB and E is the midpoint of AD, 

Then, $FE=~\dfrac{BD}{2}=\dfrac{16}{2}=8~cm$       (by mid-point theorem)

Similarly, $FG=~\dfrac{AC}{2}=\dfrac{12}{2}=6~cm$    (by mid-point theorem)

As we know that when we join the midpoints of adjacent sides of a rhombus then we get a rectangle.

Thus, quadrilateral EFGH is a rectangle.

Now, area of this rectangle $=FE~\times FG$

$=8~\times 6$

$=48~c{{m}^{2}}$

Hence, option (A) is the correct answer.

Exercise 9.1

Write the correct answer in each of the following: 

1. The median of a triangle divides it into two

(A) Triangles of equal area 

(B) Congruent triangles 

(C) Right triangles 

(D) Isosceles triangles

Ans: The correct answer option is (A).

The median of a triangle divides it into two triangles of equal area.

Hence, option (A) is the correct answer.

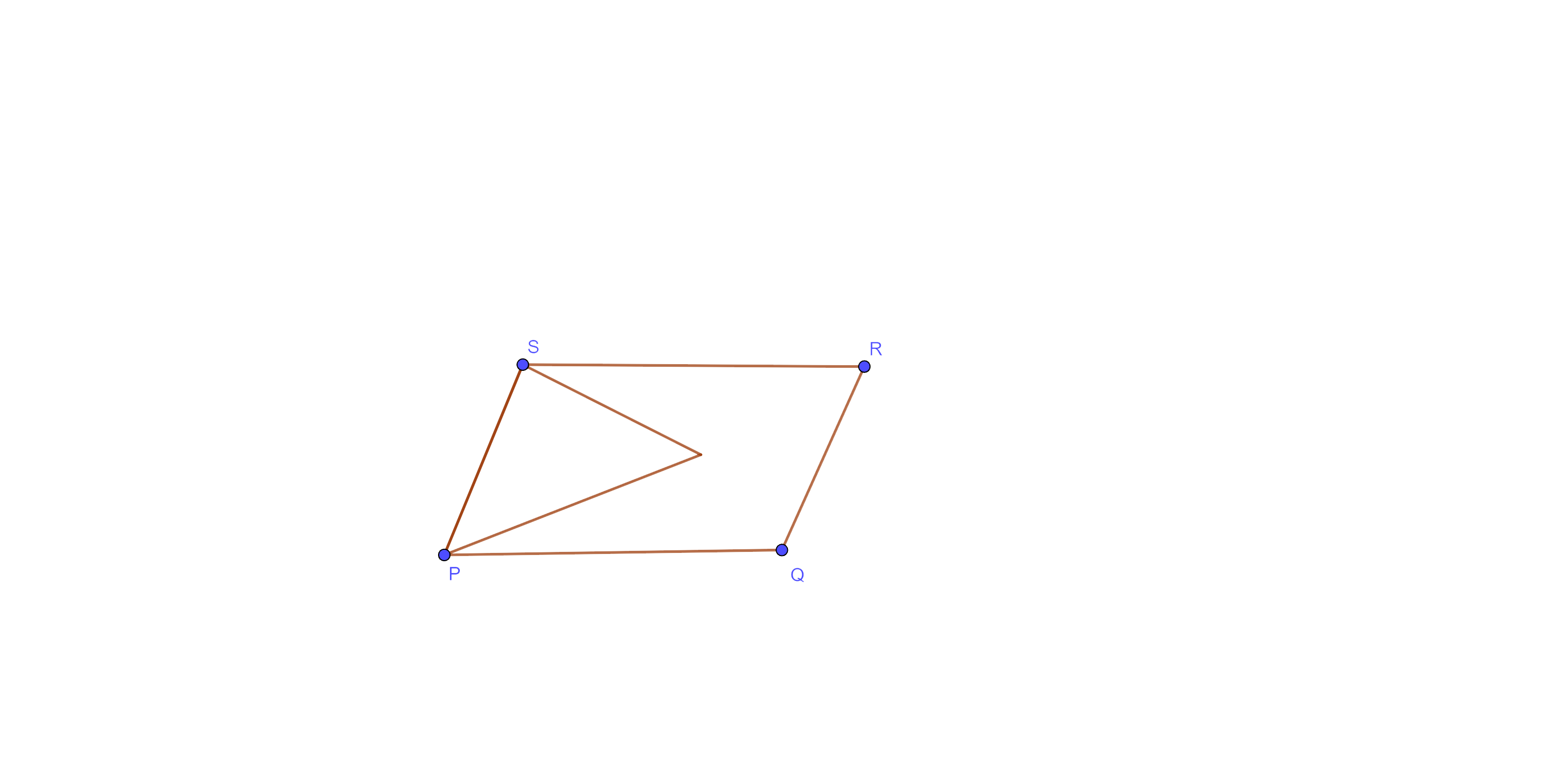
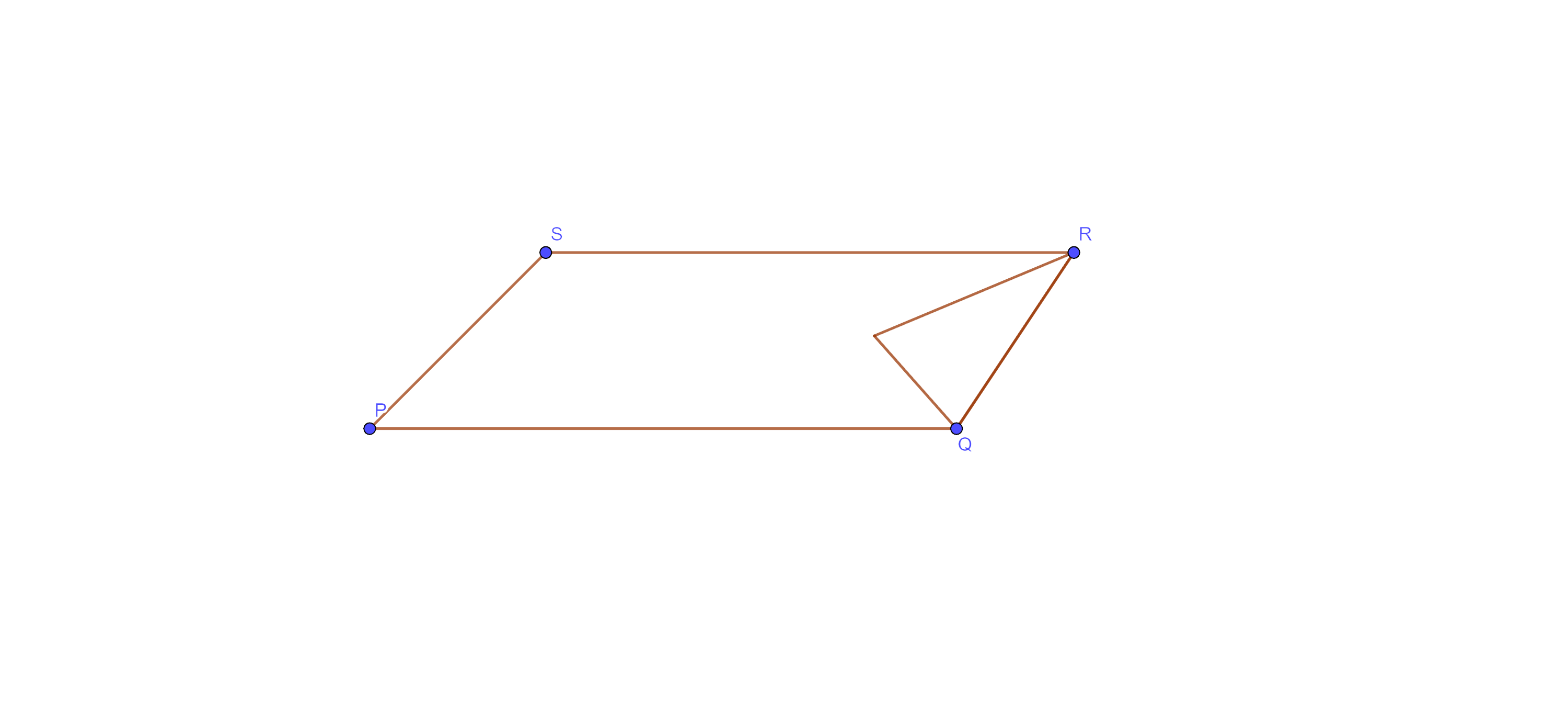
2. In which of the following figures (Fig. 9.3), you find two polygons on the same base and between the same parallels?

(A)

(B) 

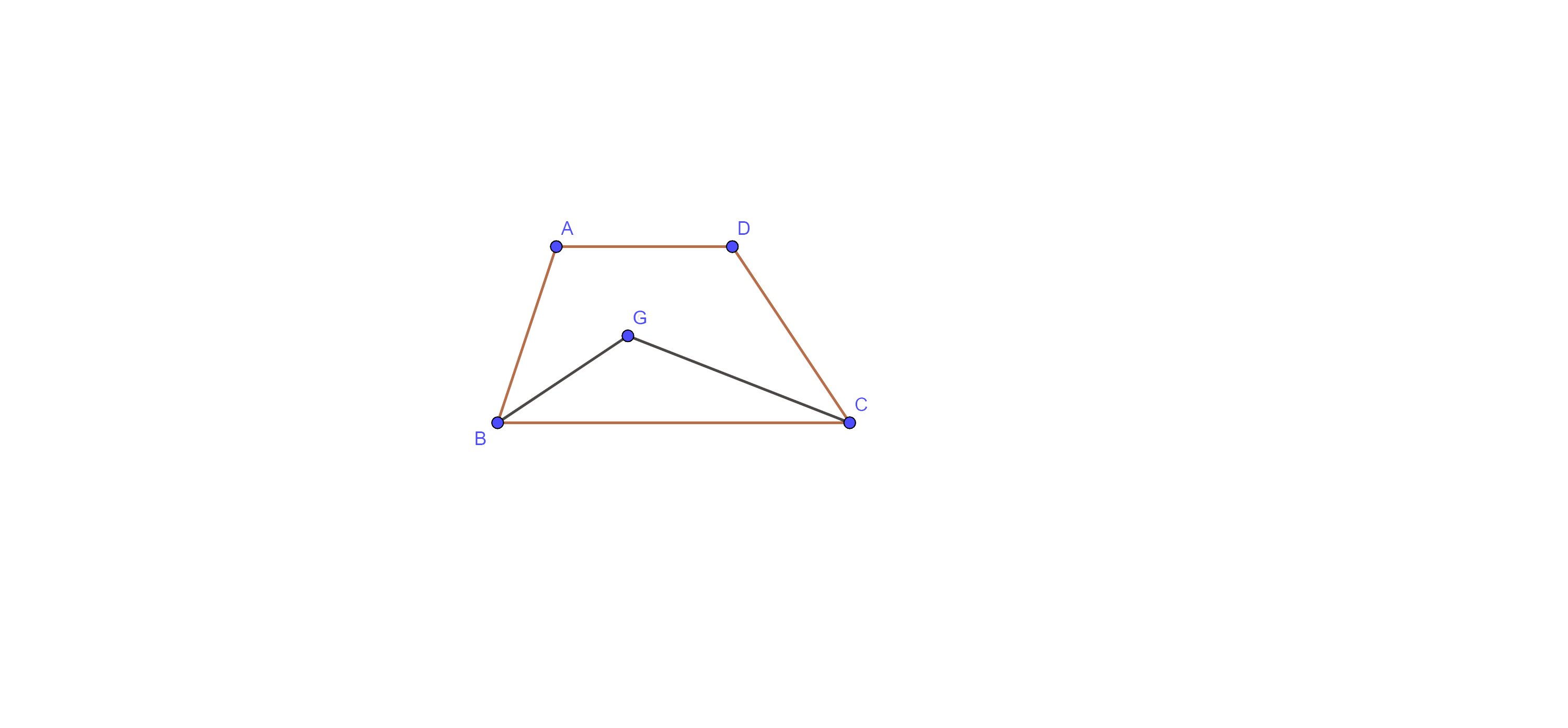
(C) 

(D) 

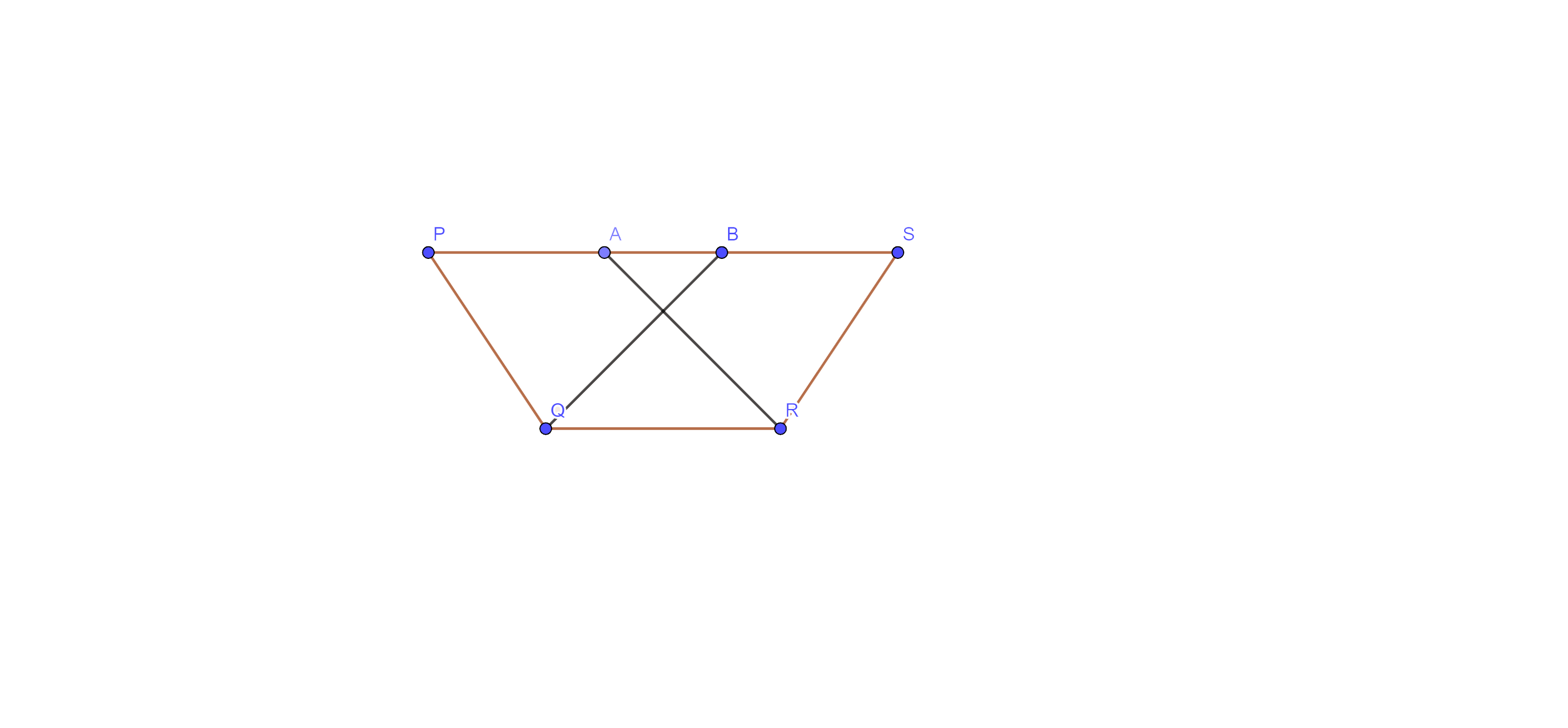
Ans: The correct answer is option (D).

Here, in figure (D), we find two polygons (parallelogram) on the same base and the same parallels. 

3. The figure obtained by joining the mid – points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is:  

(A) A rectangle of area $24~\mathbf{c}{{\mathbf{m}}^{2}}.$

(B) A square of area $25~\mathbf{c}{{\mathbf{m}}^{2}}.$

(C) A trapezium of area $24~\mathbf{c}{{\mathbf{m}}^{2}}.$

(D) A rhombus of area $24~\mathbf{c}{{\mathbf{m}}^{2}}.$

Ans: The correct answer is option (d).

Let ABCD be a rectangle in which points E, F, G and H are mid- point of sides AB, BC, CD and DA respectively.

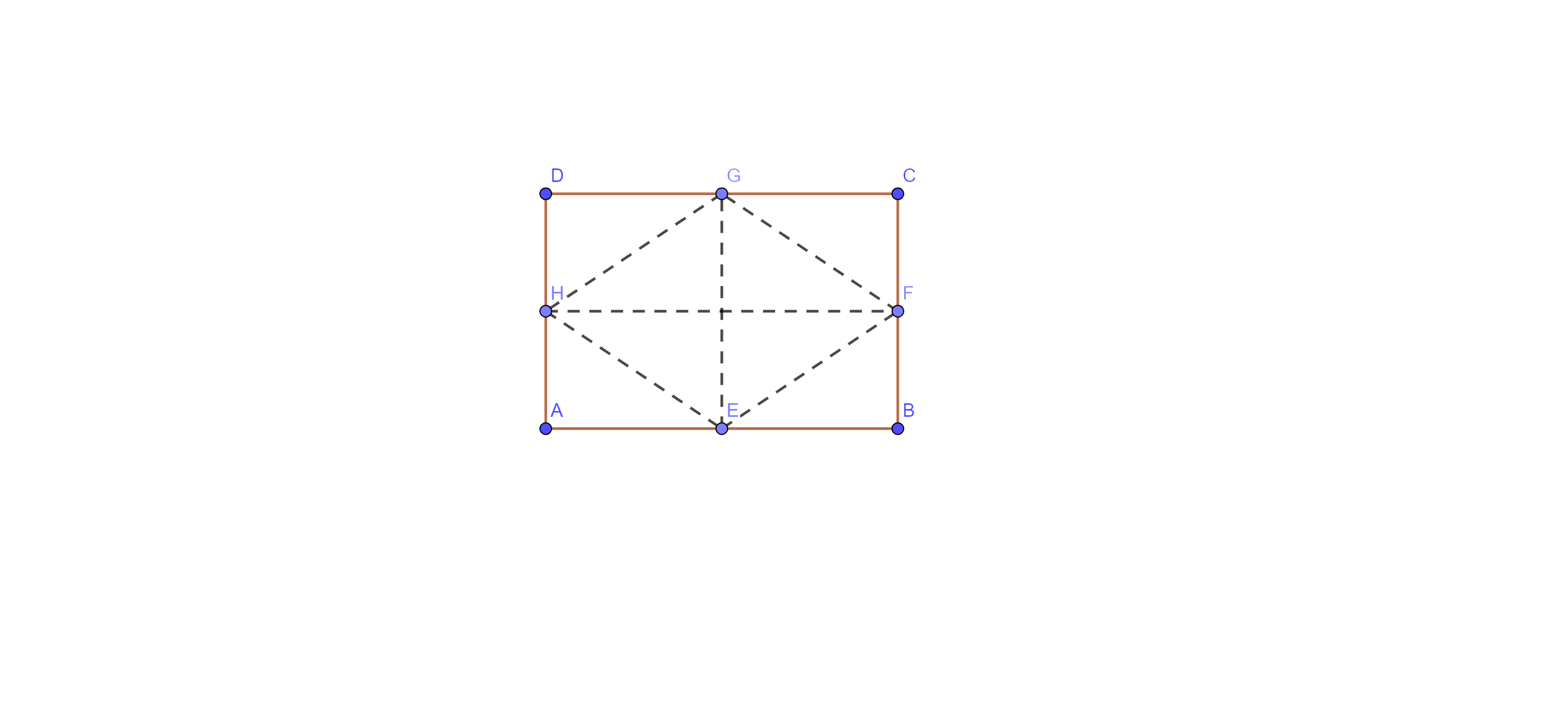
Here, AB = CD and AD = BC

Now, In $\text{ }\!\!\Delta\!\!\text{ GDH}$ and $\text{ }\!\!\Delta\!\!\text{ GCF}$

⇒ GD = GC { G is the midpoint of CD}

⇒ $\angle \text{D}=\angle \text{C }\!\!~\!\!\text{ }$  { each $90{}^\circ $}

And DH = CF {half of equal sides}

Thus, $\Delta \text{GDH}$ $\cong $ $\Delta \text{GCF}$ by S.A.S congruence.

So, $\text{GH}=\text{GF}$     {C.P.C.T}

similarly, $\text{GF}=\text{FE }\!\!~\!\!\text{ }$, $\text{FE}=\text{EH}$ and $\text{EH}=\text{GH}$

from the above equations, we get

⇒ GH = GF = FE = EH and GE $\ne \text{FH}$

Thus, in quadrilateral GFEH, all four sides are equal but diagonals are not equal.

Therefore, quad. GFEH is a rhombus.

Now, the area of this rhombus = $\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{product }\!\!~\!\!\text{ of }\!\!~\!\!\text{ both }\!\!~\!\!\text{ diagonals}$

= $\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{GE}\times \text{FH}$

= $\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{AD}\times \text{CD}$    

= $\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times 6\times 8$    

= $24\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$    

Hence, option (d) is the correct answer.

4. In Fig. 9.4, the area of parallelogram ABCD:

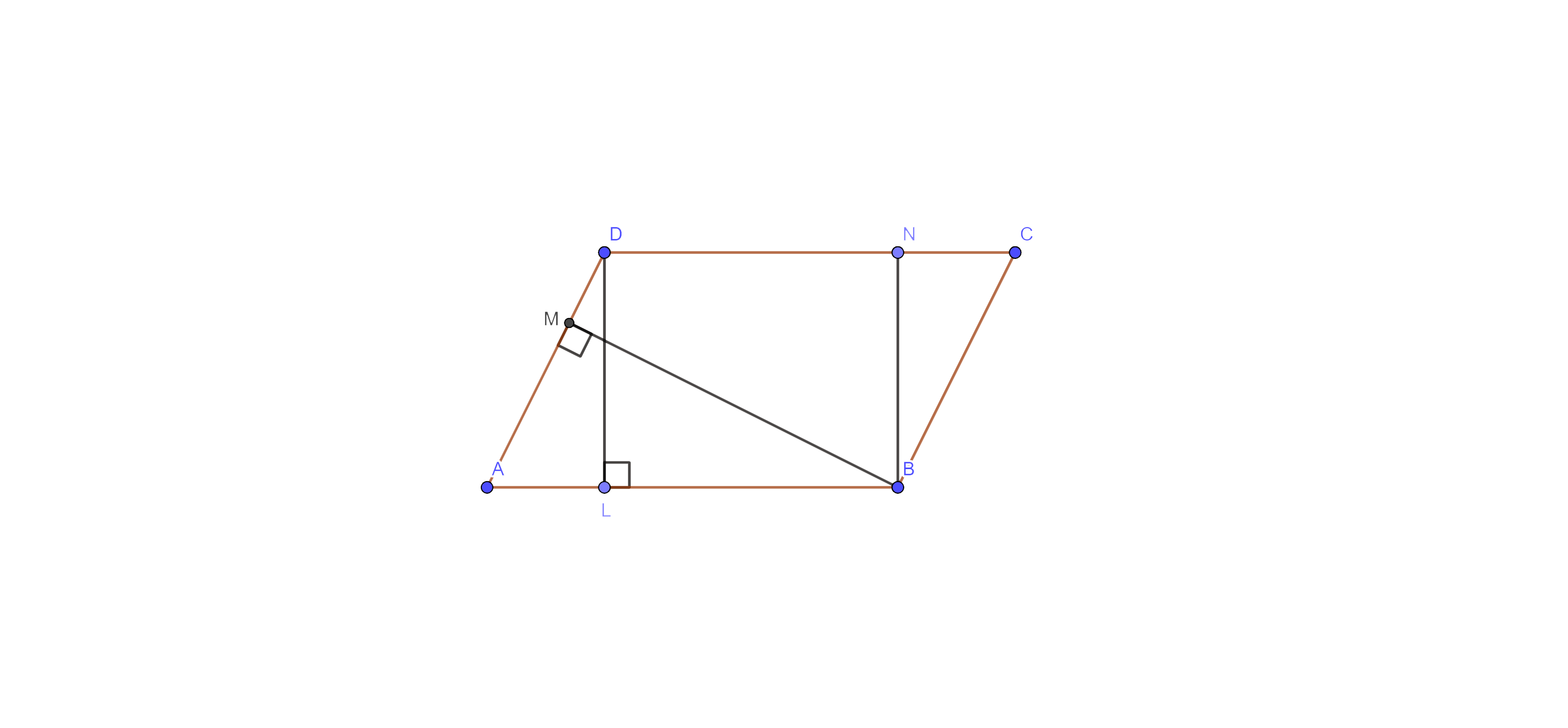
(A) $\mathbf{AB}\times \mathbf{BM}$

(B) $\mathbf{BC}\times \mathbf{BN}$

(C) $\mathbf{DC}\times \mathbf{DL}$

(D) $\mathbf{AD}\times \mathbf{DL}$

Ans: The correct answer is option (C).

We know that Area of parallelogram $=\text{Base }\!\!~\!\!\text{ }\times \text{ }\!\!~\!\!\text{ height }\!\!~\!\!\text{ }$

Here, height = DL and base = AB

Therefore,

⇒ $\text{Area }\!\!~\!\!\text{ of }\!\!~\!\!\text{ parallelogram }\!\!~\!\!\text{ }=\text{AB }\!\!~\!\!\text{ }\times \text{ }\!\!~\!\!\text{ DL}=\text{DC }\!\!~\!\!\text{ }\times \text{ }\!\!~\!\!\text{ DL}$       [AB = DC]

⇒ $\text{Area }\!\!~\!\!\text{ of }\!\!~\!\!\text{ parallelogram }\!\!~\!\!\text{ }=\text{DC }\!\!~\!\!\text{ }\times \text{ }\!\!~\!\!\text{ DL}$

Hence, option (C) is the correct answer.

5. In fig. 9.5, if parallelogram ABCD and rectangle ABEF are of equal area, then:

(A). Perimeter of ABCD = Perimeter of ABEM

(B). Perimeter of ABCD < Perimeter of ABEM

(C). Perimeter of ABCD > Perimeter of ABEM

(D). Perimeter of ABCD = $\dfrac{1}{2}~$(Perimeter of ABEM)

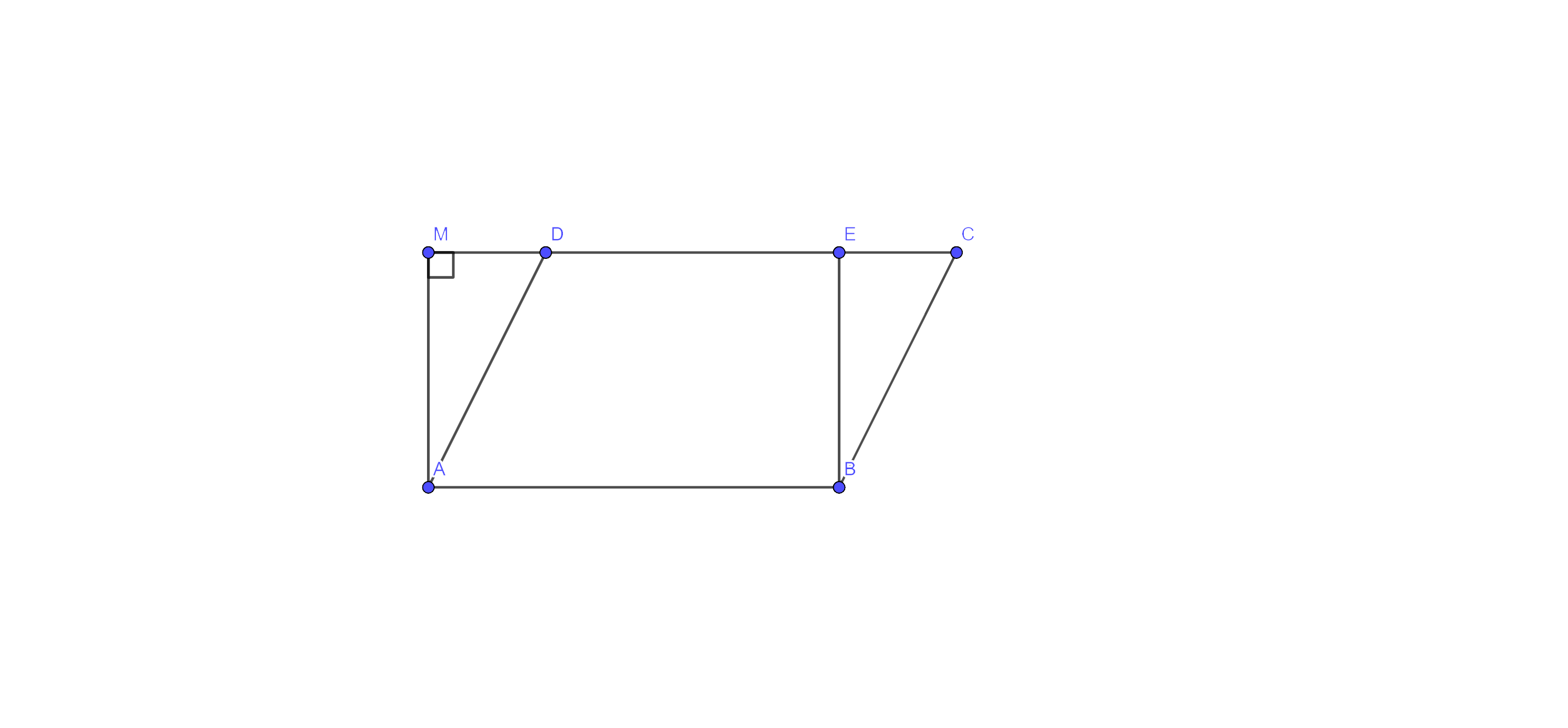
Ans: The correct answer is option (C).

If parallelogram ABCD and rectangle ABEF are of equal area, then perimeter ABCD will be greater than perimeter of ABEM because of all the line segments to a given line from a point outside it, the perpendicular is the least. Hence, option (C) is the correct answer.

6. The midpoint of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to 

(A). $\dfrac{1}{2}~\mathbf{ar}\left( \mathbf{ABC} \right)$                                 

(B). $\dfrac{1}{3}~\mathbf{ar}\left( \mathbf{ABC} \right)$

(C) $\dfrac{1}{4}~\mathbf{ar}\left( \mathbf{ABC} \right)$                                  

(D) $~\mathbf{ar}\left( \mathbf{ABC} \right)$

Ans: The correct answer is option (A).

Let the points F, D and E are the mid-point of side AB, BC and AC respectively.

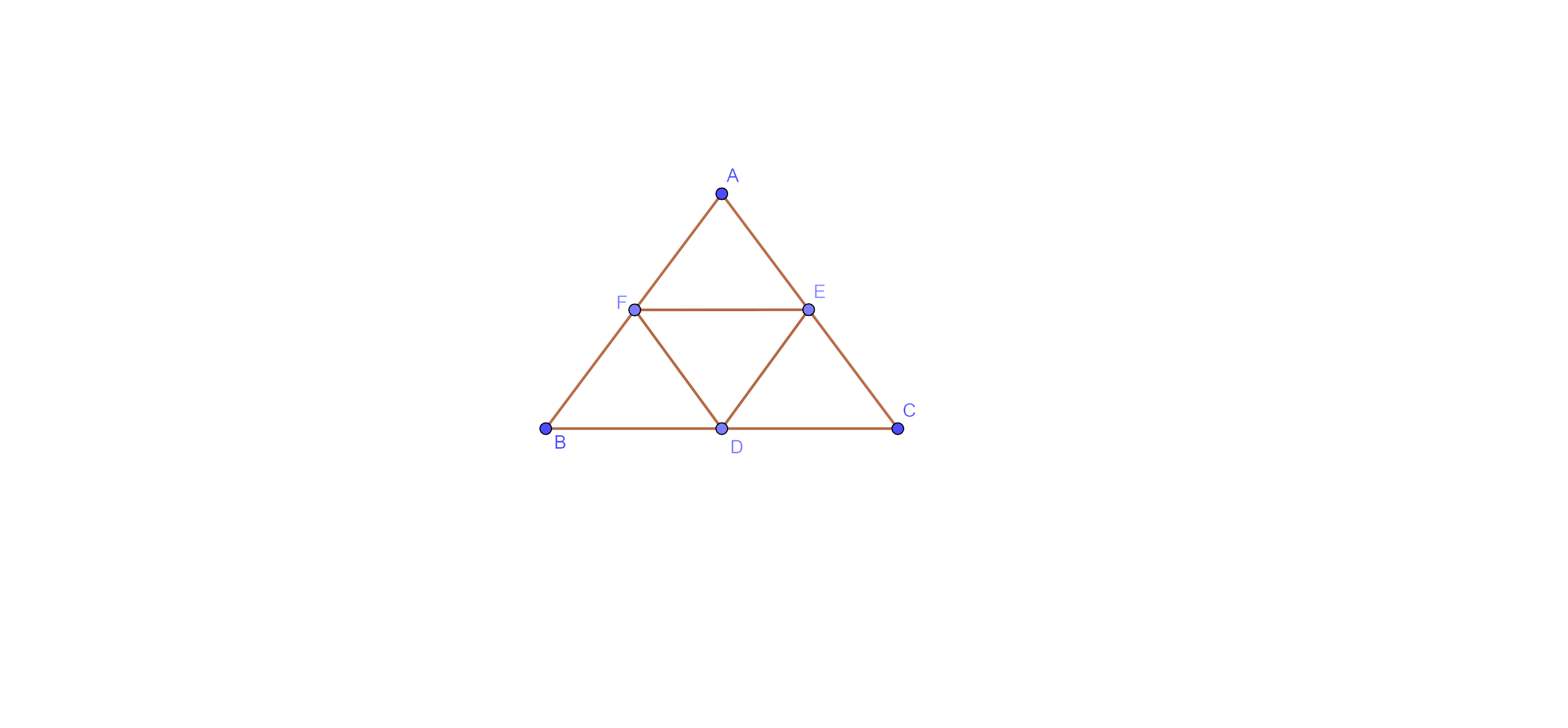
Here, F and E are the mid-point of sides AB and AC respectively.

Thus, $\text{EF}\parallel \text{BC}$ and  $\text{EF}=\dfrac{\text{BC}}{2}$  by mid-point theorem.

⇒ $\text{EF}\parallel \text{BC}$ and  $\text{EF}=\text{BD}$.

Therefore, quad. BDEF is a parallelogram.

Similarly, quadrilateral FDCE and AFDE are parallelograms.

And we know that the diagonal of a parallelogram divides it into two triangles of equal areas.

Thus, $\text{ar}\left( \Delta \text{BFD} \right)=\text{ar}\left( \Delta \text{FDE} \right)$ ………(i)

⇒ $\text{ar}\left( \Delta \text{CDE} \right)=\text{ar}\left( \Delta \text{FDE} \right)$ ………… (ii)

⇒ $\text{ar}\left( \Delta \text{AFE} \right)=\text{ar}\left( \Delta \text{FDE} \right)$ ……………(iii)

From eq (i), (ii) and (iii)

⇒ $\text{ar}\left( \Delta \text{BFD} \right)=\text{ar}\left( \Delta \text{AFE} \right)=\text{ar}\left( \Delta \text{CDE} \right)=\text{ar}\left( \Delta \text{FDE} \right)$

Now,

⇒ \[\text{ar}\left( \Delta \text{ABC} \right)=\text{ }\!\!~\!\!\text{ ar}\left( \Delta \text{BFD} \right)+\text{ar}\left( \Delta \text{AFE} \right)+\text{ar}\left( \Delta \text{CDE} \right)+\text{ar}\left( \Delta \text{FDE} \right)\]

⇒ $\text{ar}\left( \Delta \text{ABC} \right)=\text{ }\!\!~\!\!\text{ ar}\left( \Delta \text{BFD} \right)+\text{ar}\left( \Delta \text{BFD} \right)+\text{ar}\left( \Delta \text{BFD} \right)+\text{ar}\left( \Delta \text{BFD} \right)$

\[\Rightarrow \text{ar}\left( \Delta \text{ABC} \right)=4\times \text{ar}\left( \Delta \text{BFD} \right)\]

 $\Rightarrow \text{ar}\left( \Delta \text{BFD} \right)=\dfrac{\text{ar}\left( \Delta \text{ABC} \right)}{4}$

$\Rightarrow \dfrac{1}{2}\times \text{parallelogram }\!\!~\!\!\text{ BDEF}=\dfrac{\text{ar}\left( \Delta \text{ABC} \right)}{4}$

$\Rightarrow \text{Parallelogram }\!\!~\!\!\text{ BDEF}=\dfrac{1}{2}\text{ar}\left( \Delta \text{ABC} \right)$

Hence, option (A) is the correct answer.

7. Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is

\[\left( \text{A} \right)\text{ }\!\!~\!\!\text{ 1 }\!\!~\!\!\text{ : }\!\!~\!\!\text{ 2}\]               

(B) $\text{1 }\!\!~\!\!\text{ : }\!\!~\!\!\text{ 1 }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$           

(C) $\text{2 }\!\!~\!\!\text{ : }\!\!~\!\!\text{ 1}$           

(D) $\text{3 }\!\!~\!\!\text{ : }\!\!~\!\!\text{ 1}$

Ans: The correct answer is option (B).

We know that parallelograms on the same or equal bases and between the same parallels are equal in area.

Thus, the ratio of their area is 1:1.

Hence, option (B) is the correct answer.

8. ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD. 

(A). Is a rectangle

(B). Is always a rhombus

(C) Is a parallelogram

(D) need not be any of (A), (B) or (C) 

Ans: The correct answer is option(D).

We know that the diagonal of a parallelogram divides it into two triangles of equal area and a rectangle and a rhombus are also parallelograms. But it may be a kite as the diagonal of a kite divides it into two triangles of equal areas. Then ABCD need not be any of (a), (b) or (c). 

Hence, option (D) is the correct answer.

9. If a triangle and a parallelogram are on the same base and between the same parallels, Then the ratio of the area of the triangle to the area of the parallelogram is:

(A) 1:3 

(B) 1:2 

(C) 3:1

(D) 1:4 

Ans: The correct answer is option (B). 

Let $\Delta \text{ABC}$ and parallelogram ABCD are on the same base DC and between the same parallels $\text{DC}\parallel \text{AB}.$

And, AN is the height for triangle as well as for parallelogram.

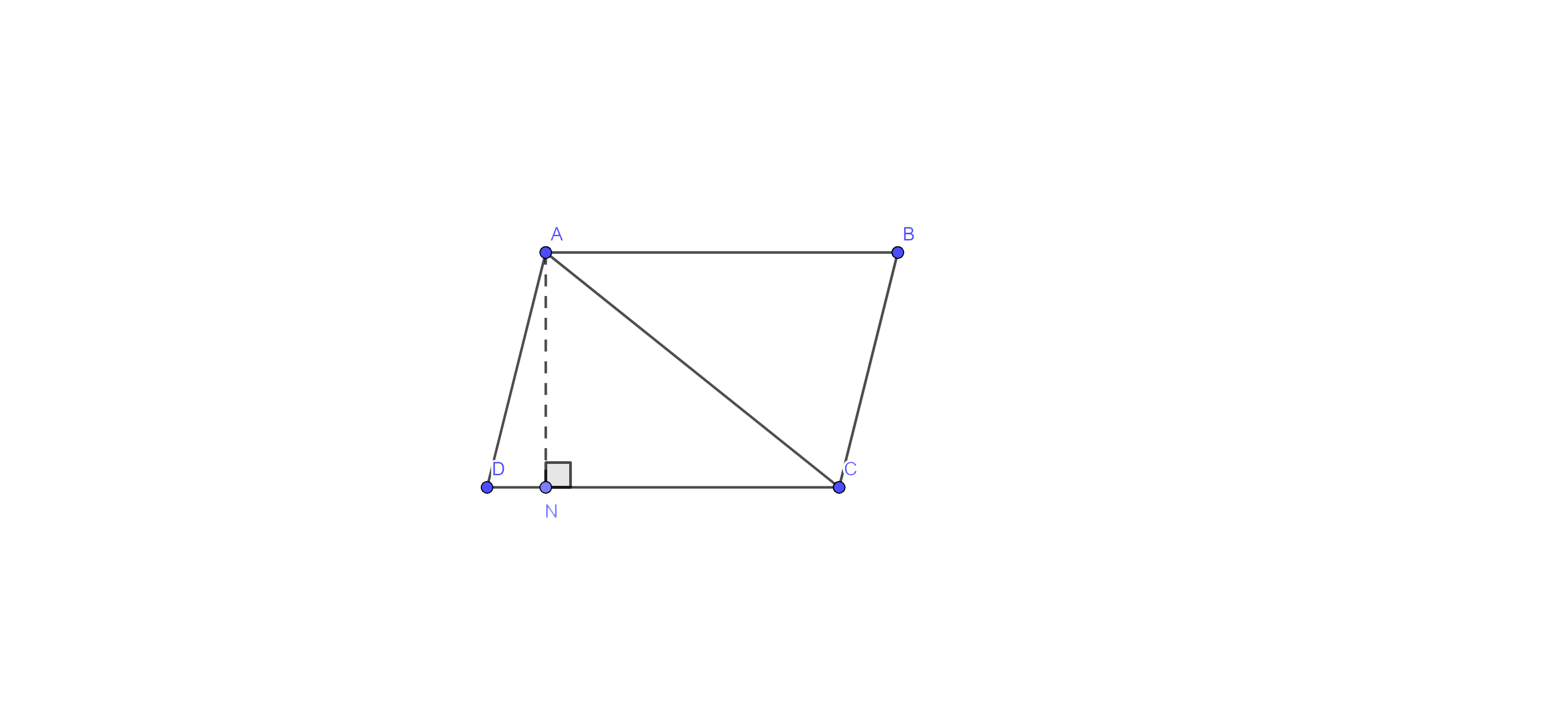
Now, $\text{ar}\left( \parallel \text{ABCD} \right)=\text{base }\!\!~\!\!\text{ }\times \text{height }\!\!~\!\!\text{ }$

⇒$\text{ar}\left( \parallel \text{ABCD} \right)=\text{DC}\times \text{AN}$ ………(i)

And $\text{ar}\left( \Delta \text{ADC} \right)=\dfrac{1}{2}\times \text{base }\!\!~\!\!\text{ }\times \text{height}$

⇒ $\text{ar}\left( \Delta \text{ADC} \right)=\dfrac{1}{2}\times \text{DC }\!\!~\!\!\text{ }\times \text{AN}$

⇒  $\text{ar}\left( \Delta \text{ADC} \right)=\dfrac{1}{2}\times \text{ar}\left( \parallel \text{ABCD} \right)$

⇒  $\dfrac{\text{ar}\left( \Delta \text{ADC} \right)}{\text{ar}\left( \parallel \text{ABCD} \right)}=\dfrac{1}{2}$

Thus, the required ratio of the area of the triangle to the area of parallelogram is $1\text{ }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ }2$.

Hence, option (B) is the correct answer.

10. ABCD is a trapezium with parallel sides $\mathbf{AB}=\mathbf{a}~\mathbf{cm}$ and $\mathbf{D}=\mathbf{b}~\mathbf{cm}$ Fig (9.6). E and F are the midpoints of the non-parallel sides. The ratio of $\mathbf{ar}\left( \mathbf{ABFE} \right)~$and $\mathbf{ar}\left( \mathbf{EFCD} \right)$ is 

(A) $\mathbf{a}~:\mathbf{b}$

(B) $\left( 3\mathbf{a}+\mathbf{b} \right)~:\left( \mathbf{a}+3\mathbf{b} \right)$

(C) $\left( \mathbf{a}+3\mathbf{b} \right)~:\left( 3\mathbf{a}+\mathbf{b} \right)$

(D) $\left( 2\mathbf{a}+\mathbf{b} \right)~:\left( 3\mathbf{a}+\mathbf{b} \right)$

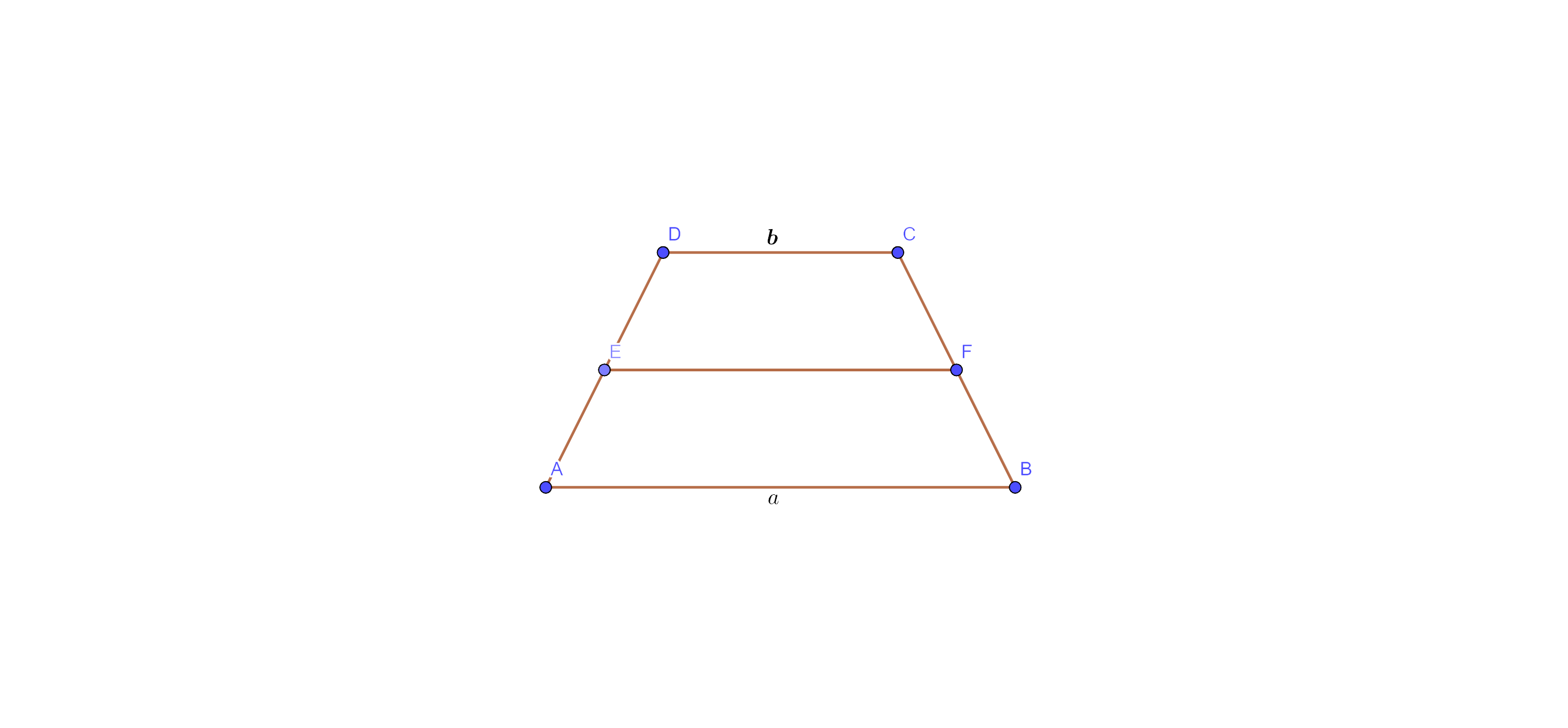
Ans: Option (B) is the correct answer.

ABCD is a trapezium in which $\text{AB}\parallel \text{DC}.$ E and F are the mid-points of AD and BC, so $\text{EF}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\left( \text{a}+\text{b} \right).$

Here, ABEF and EFCD are also trapeziums.

$\text{ar}\left( \text{ABEF} \right)=\dfrac{1}{2}\times \text{sum }\!\!~\!\!\text{ of }\!\!~\!\!\text{ parallels }\!\!~\!\!\text{ side}\times \text{height}$ 

$=\dfrac{1}{2}\times \left( \text{AB}+\text{EF} \right)\times \text{h}$

$=\dfrac{1}{2}\times \left[ \text{a}+\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\left( \text{a}+\text{b} \right) \right]\times \text{h}$

$\text{ar}\left( \text{ABEF} \right)$  $=\dfrac{1}{4}\times \left( 3\text{a}+\text{b} \right)\times \text{h}$ ……….. eq (i)

Now, $\text{ar}\left( \text{EFCD} \right)=\dfrac{1}{2}\times \left( \text{EF}+\text{CD} \right)\times \text{h}$

$=\dfrac{1}{2}\times \left[ \dfrac{1}{2}\left( \text{a}+\text{b} \right)+\text{b} \right)]\times \text{h}$

$=\dfrac{1}{4}\times \left( \text{a}+3\text{b} \right)\times \text{h}$

$\therefore \text{ar}\left( \text{EFCD} \right)=\text{ }\!\!~\!\!\text{ }\dfrac{1}{4}\times \left( \text{a}+3\text{b} \right)\times \text{h}$  …………….. eq (ii)

Now, divide eq (i) by (ii), we get

⇒$\text{ }\!\!~\!\!\text{ }\dfrac{\text{ar}\left( \text{ABEF} \right)}{\text{ar}\left( \text{EFCD} \right)}=\dfrac{\dfrac{1}{4}\times \left( 3\text{a}+\text{b} \right)\times \text{h}}{\dfrac{1}{4}\times \left( \text{a}+3\text{b} \right)\times \text{h}}$

⇒$\text{ }\!\!~\!\!\text{ }\dfrac{\text{ar}\left( \text{ABEF} \right)}{\text{ar}\left( \text{EFCD} \right)}=\dfrac{\left( 3\text{a}+\text{b} \right)}{\left( \text{a}+3\text{b} \right)}$

Hence, option (B) is correct.

(C) Short Answer Questions with Reasoning 

Write True or False and justify your answer:

Sample Question 1: If P is any point on the median AD of a $\Delta ~ABC$, then $ar\left( ABP \right)\ne ar\left( ACP \right).$

Ans: Here, we have P is any point on the median AD of a $\Delta ~ABC$.

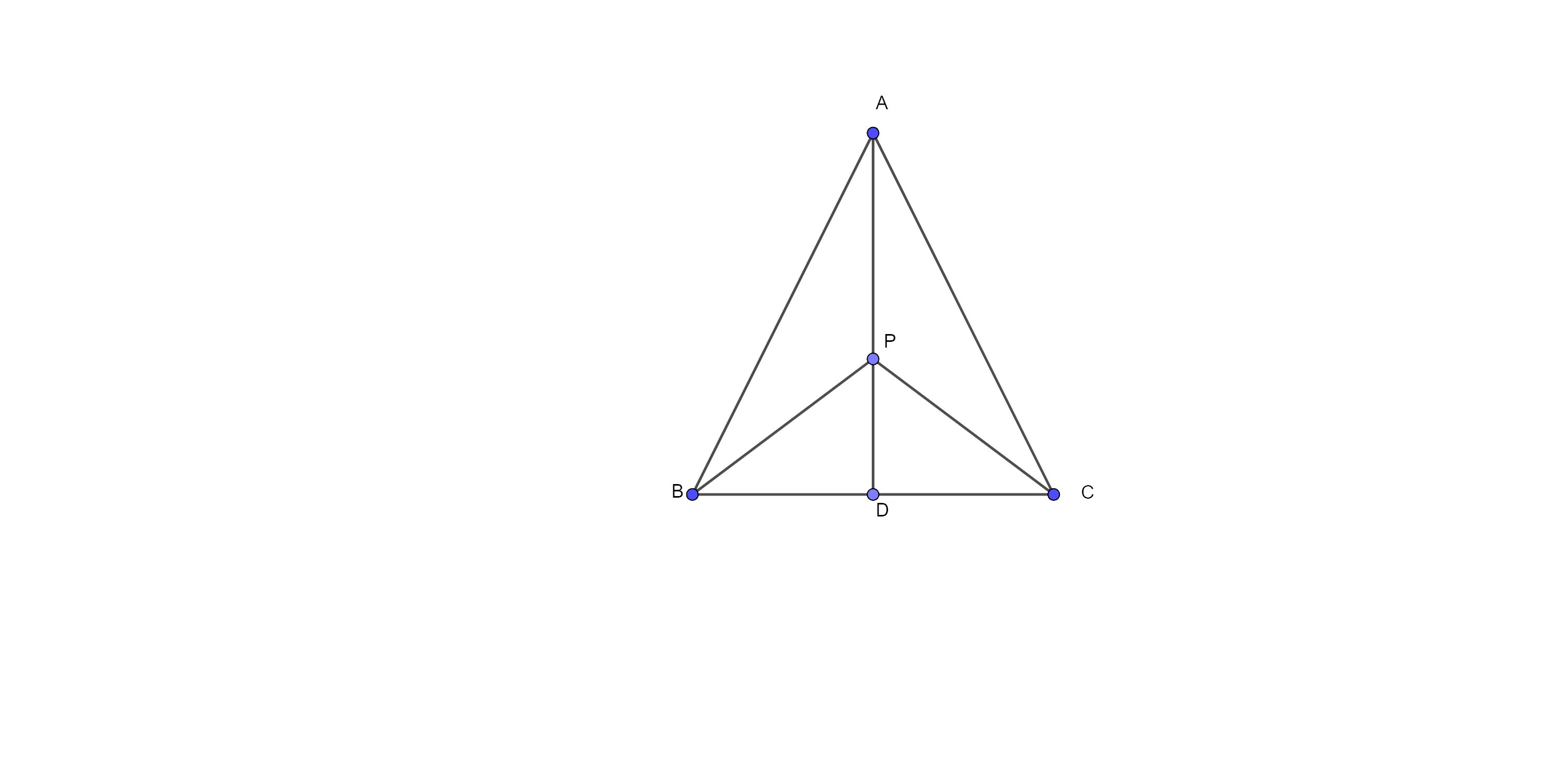
As we know that the median of a triangle divides it into two triangles of equal area. 

Therefore, $ar\left( \Delta ADB \right)=ar\left( \Delta ADC \right)$ …………….. (i)

Here, PD is the median of $\Delta PBC$.

So, $ar\left( \Delta PDB \right)=ar\left( \Delta PDC \right)$ …………….. (ii)

Now, subtracting eq (ii) from (i), we have 

⇒ \[ar\left( \Delta ADB \right)-ar\left( \Delta PDB \right)=ar\left( \Delta ADC \right)-ar\left( \Delta PDC \right)\]

⇒ $ar\left( \Delta ABP \right)=ar\left( \Delta ACP \right)$

Thus, the given statement is False.

Sample Question 2: If in Fig. 9.7, PQRS and EFRS are two parallelograms, then $ar\left( MFR \right)=\dfrac{1}{2}~ar\left( PQRS \right)$. 

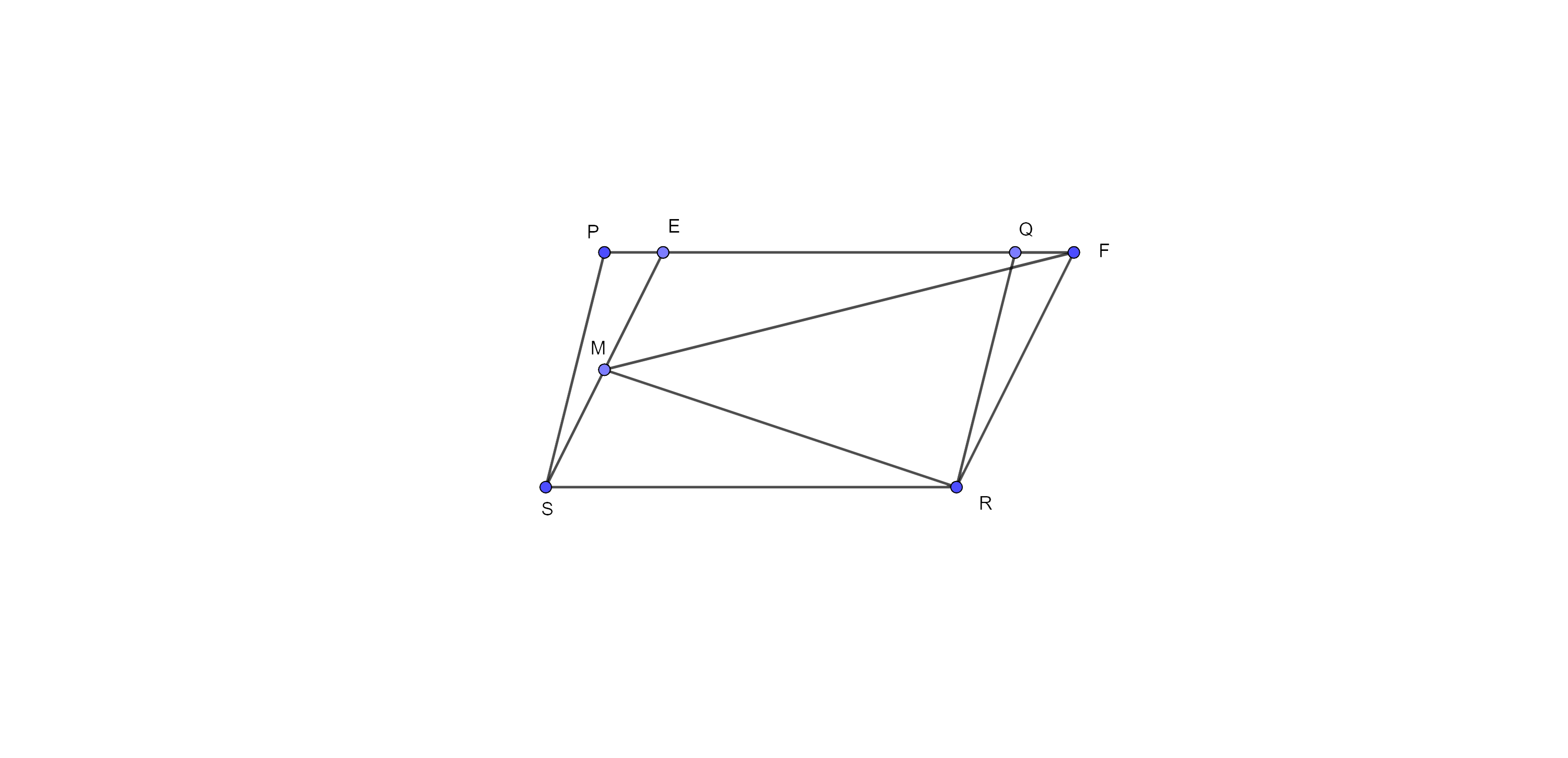
Ans: Here, parallelograms PQRS and EFRS are on the same base RS and between the same parallel lines. 

Therefore, $ar\left( PQRS \right)=ar\left( EFRS \right)$ …………. (i)

Now, parallelogram EFRS and $\Delta MFR$ are on the same base and between the same parallel lines. 

As we know, the area of the triangle is equal to the half of the parallelogram form on the same base and lies between the same two parallel lines.

So, $ar\left( \Delta MFR \right)=\dfrac{1}{2}~ar\left( EFRS \right)$ …………. (ii)

Now, from eq (i) and (ii), we get

⇒ $ar\left( \Delta MFR \right)=\dfrac{1}{2}~ar\left( PQRS \right)$

Hence, the given statement is True.

Exercise 9.2

Write True or False and justify your answer:

1. ABCD is a parallelogram and X is the midpoint of AB. If $\mathbf{ar}\left( \mathbf{AXCD} \right)=~24~\mathbf{c}{{\mathbf{m}}^{2}},$ then $\mathbf{ar}\left( \mathbf{ABC} \right)=~24~\mathbf{c}{{\mathbf{m}}^{2}}.$

Ans: Here, we have ABCD is a parallelogram and X is the midpoint of AB.

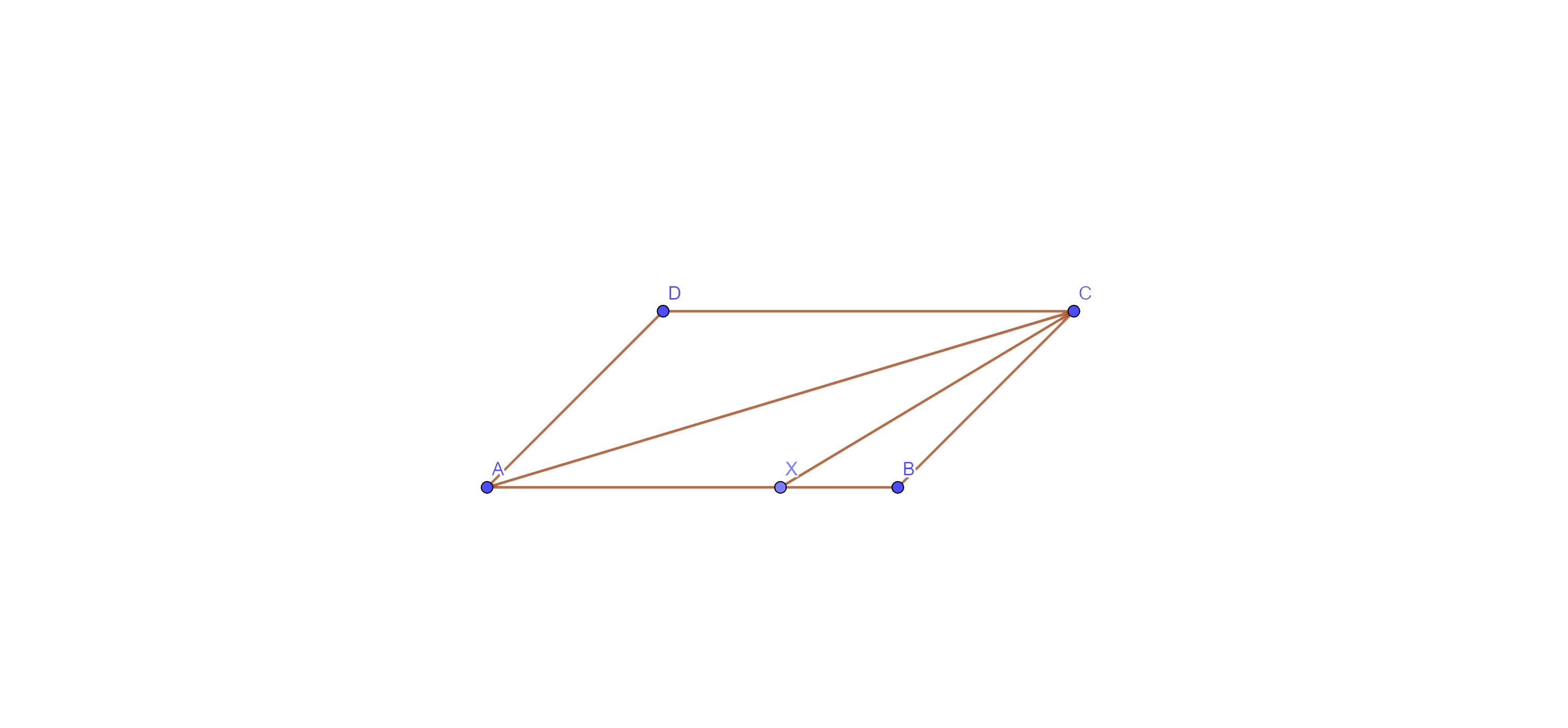
Now, $\text{ar}\left( \text{ABCD} \right)=\text{ar}\left( \text{AXCD} \right)+\text{ar}\left( \Delta \text{XBC} \right)$ ……. eq (i) 

And we know that the diagonal AC of a parallelogram divides it into two triangles of equal area.

Then, $\text{ar}\left( \text{ABCD} \right)=2\times \text{ar}\left( \Delta \text{ABC} \right)$ ……. eq (ii)

Again, X is the midpoint of AB, so

⇒ $\text{ar}\left( \Delta \text{XBC} \right)=\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABC} \right)$ ……. eq (iii)

Now, from eq (i), (ii) and (iii)

⇒ $2\times \text{ar}\left( \Delta \text{ABC} \right)=\text{ar}\left( \text{AXCD} \right)+\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABC} \right)\text{ }\!\!~\!\!\text{ }$ 

⇒ $2\times \text{ar}\left( \Delta \text{ABC} \right)-\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABC} \right)=\text{ar}\left( \text{AXCD} \right)\text{ }\!\!~\!\!\text{ }$ 

⇒ $\dfrac{3}{2}\times \text{ar}\left( \Delta \text{ABC} \right)=24$

⇒ $\text{ar}\left( \Delta \text{ABC} \right)=24\times \dfrac{2}{3}$

⇒ $\text{ar}\left( \Delta \text{ABC} \right)=16\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}.$

Thus, $\text{ar}\left( \Delta \text{ABC} \right)\text{ }\!\!~\!\!\text{ is }\!\!~\!\!\text{ }16\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$.

Hence, the given statement is false.

2. PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then $\mathbf{ar}\left( \mathbf{PAS} \right)=30~\mathbf{c}{{\mathbf{m}}^{2}}.$

Ans: Here, we have, point A is any point on PQ, therefore, PA < PQ.

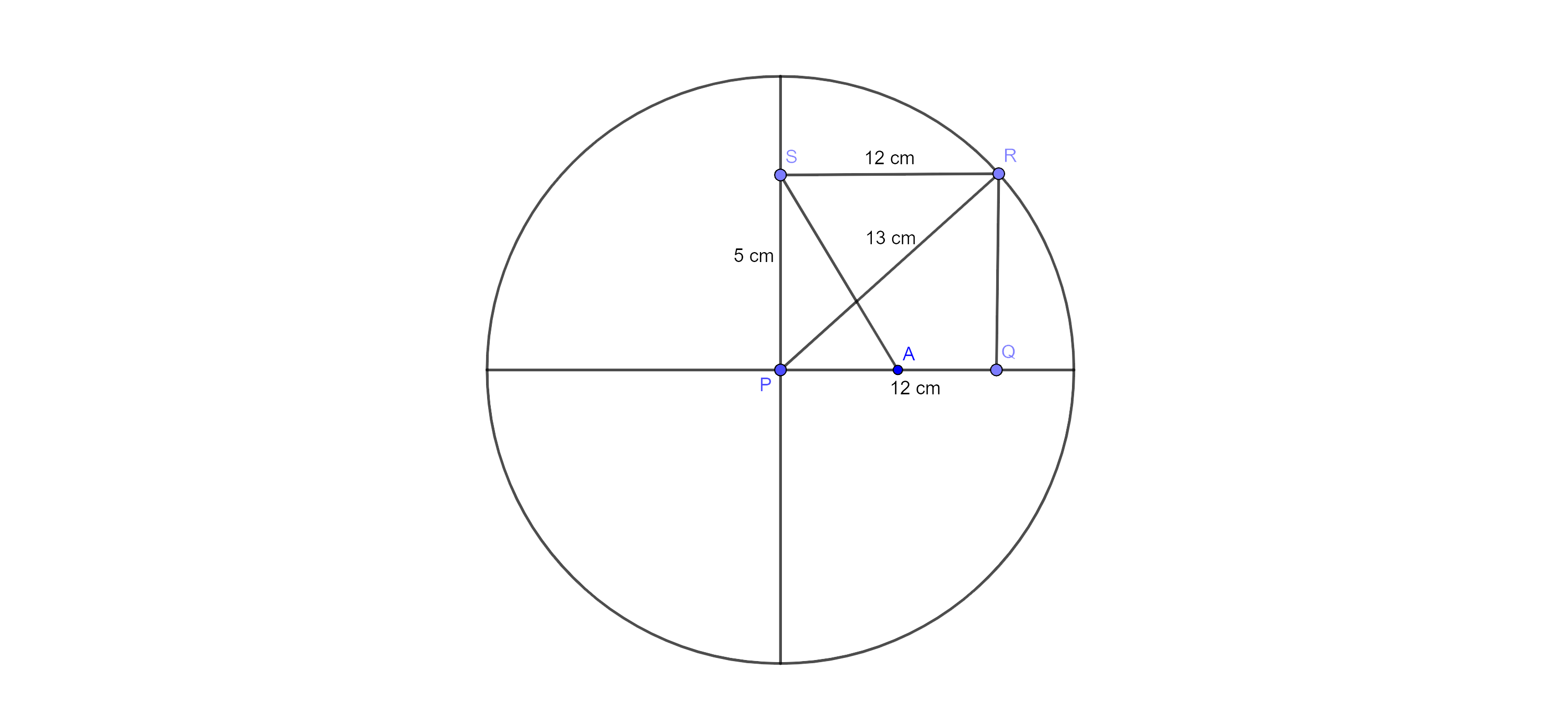
Now, In $\Delta \text{PSR},$ by Pythagoras theorem

⇒ $\text{P}{{\text{R}}^{2}}=\text{P}{{\text{S}}^{2}}+\text{S}{{\text{R}}^{2}}$

⇒ ${{13}^{2}}={{5}^{2}}+\text{S}{{\text{R}}^{2}}$

⇒ $169=25+\text{S}{{\text{R}}^{2}}$

⇒ $144=\text{S}{{\text{R}}^{2}}$

⇒ $\sqrt{144}=\text{SR}$

⇒ $12\text{ }\!\!~\!\!\text{ cm}=\text{SR}$

⇒ $\text{SR}=12\text{ }\!\!~\!\!\text{ cm}$

Now, $\text{ar}\left( \Delta \text{PQR} \right)=\dfrac{1}{2}\times \text{PQ}\times \text{RQ}$

$=\dfrac{1}{2}\times 12\times 5$                  $\left[\because PQ = SR, PS = RQ \right]$

 $=30\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$       

And we have, PA < PQ

⇒$\dfrac{1}{2}\times \text{PA}\times \text{PS}<\dfrac{1}{2}\times \text{PQ}\times \text{PS}$                

⇒$\text{ar}\left( \Delta \text{PAS} \right)<\text{ar}\left( \Delta \text{PQR} \right)$                

⇒$\text{ar}\left( \Delta \text{PAS} \right)<30\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$              

Hence, the given statement is false.

3. PQRS is a parallelogram whose area is $180~\mathbf{c}{{\mathbf{m}}^{2}}$ and A is any point on the diagonal QS. The area of $\Delta \mathbf{ASR}=90~\mathbf{c}{{\mathbf{m}}^{2}}.$

Ans: Here, PQRS is a parallelogram.

And we know that the diagonal (QS) of a parallelogram divides parallelogram into two triangles of equal area, so

$\therefore \text{ar}\left( \Delta \text{QRS} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \parallel \text{gm }\!\!~\!\!\text{ PQRS} \right)$ 

$=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times 180$

$=90\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$

Since, point A is any point on SQ, Therefore, 

⇒ $\text{ar}\left( \Delta \text{ASR} \right)<\text{ar}\left( \Delta \text{QRS} \right)$

Hence, $\text{ar}\left( \Delta \text{ASR} \right)<90\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}.$

Hence, the given statement is false.

4. ABC and BDE are two equilateral triangles such that D is the mid- point of BC. Then $\mathbf{ar}\left( \mathbf{BDE} \right)=\dfrac{1}{4}~\mathbf{ar}~\left( \mathbf{ABC} \right)$.

Ans: Here, ABC and BDE are two equilateral triangles such that D is the mid- point of BC.

Let each side of triangle ABC be $\text{x}.$

Again, D is the midpoint of BC, so each side of triangle BDE is $\text{ }\!\!~\!\!\text{ }\dfrac{\text{x}}{2}$ .

Now, $\dfrac{\text{ar}\left( \Delta \text{BDE} \right)}{\text{ar}\left( \Delta \text{ABC} \right)}=\dfrac{\dfrac{\sqrt{3}}{4}{{\left( \dfrac{\text{x}}{2} \right)}^{2}}}{\dfrac{\sqrt{3}}{4}{{\left( \text{x} \right)}^{2}}}\text{ }\!\!~\!\!\text{ }$

 ⇒ $\dfrac{\text{ar}\left( \Delta \text{BDE} \right)}{\text{ar}\left( \Delta \text{ABC} \right)}$ $=\dfrac{1}{4}$

⇒ $\text{ar}\left( \Delta \text{BDE} \right)$ $=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{ABC} \right)$

Hence, the given statement is true.

5. In fig. 9.8, ABCD and EFGD are two parallelograms and G is the mid – point of CD. Then $\mathbf{ar}\left( \mathbf{DPC} \right)=\dfrac{1}{2}~\times \mathbf{ar}\left( \mathbf{EFGD} \right).$

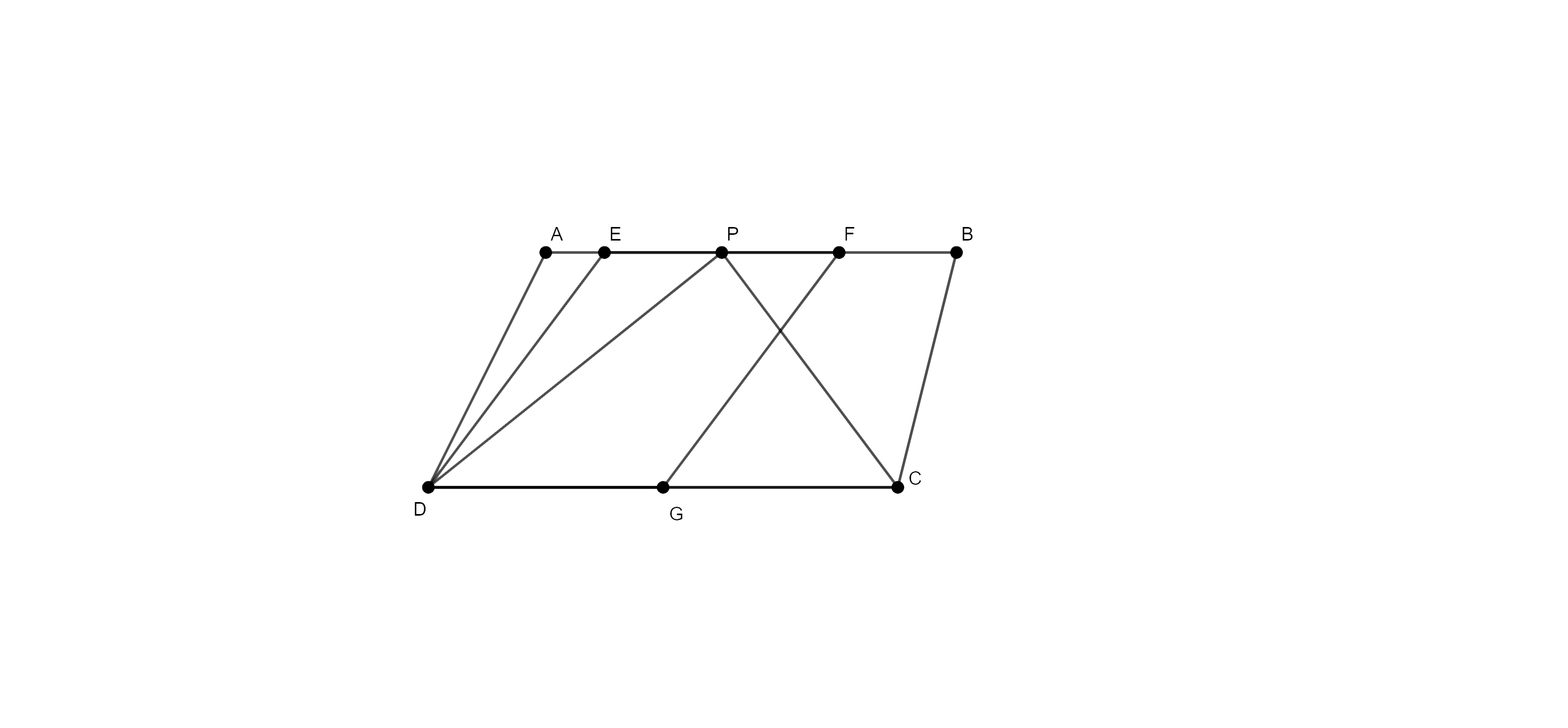
Ans: As $\Delta \text{DPC}$ and $\parallel \text{gm}$ ABCD are on the same base DC and between the same parallels AB and DC, So

⇒ $\text{ar}\left( \text{DPC} \right)=\dfrac{1}{2}\times \text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$ ……….. eq(i) 

As, $\dfrac{\text{ar}\left( \text{EFGD} \right)}{\text{ar}\left( \text{ABCD} \right)}=\text{ }\!\!~\!\!\text{ }\dfrac{\text{DG }\!\!~\!\!\text{ }\times \text{h}}{\text{DC}\times \text{h}}=\dfrac{\text{DG}}{2\text{ }\!\!~\!\!\text{ DG}}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }$   (G is the mid -point of DC)

⇒ $\text{ar}\left( \text{EFGD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \text{ABCD} \right)$ ………… eq (ii)

Now, from eq (i) and (ii), we get

⇒ $\text{ar}\left( \text{DPC} \right)=\text{ar}\left( \text{EFGD} \right)$

Hence, the given statement is false.

(D)  Short Answer Questions

Sample Question 1: PQRS is a square. T and U are, respectively, the mid-points of PS and QR (Fig. 9.9). Find the area of $\Delta OTS$, if PQ = 8 cm, where O is the point of intersection of TU and QS.

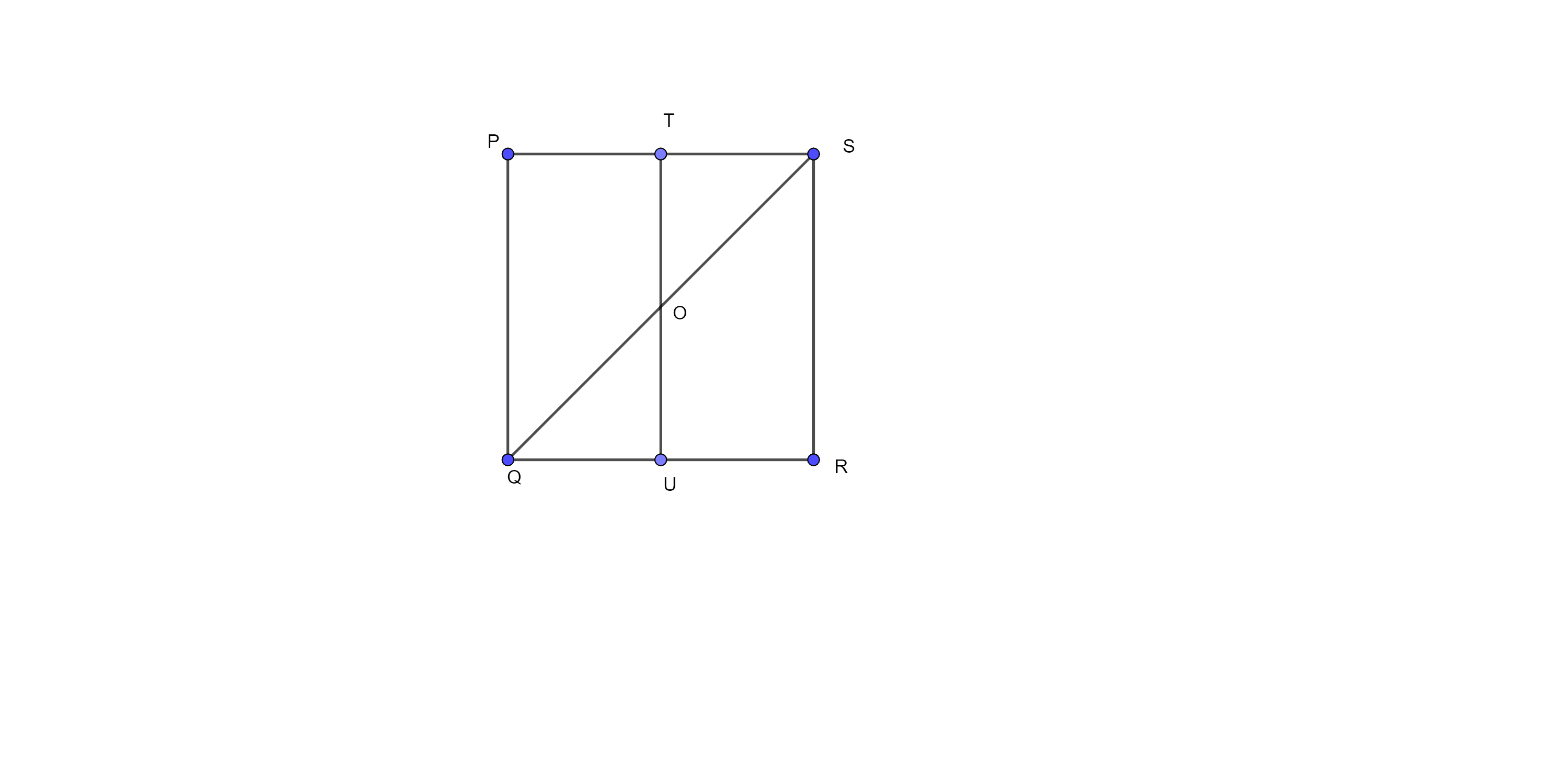
Ans: Here, we have PQRS as a square. T and U are respectively, the mid-points of PS and QR and PQ = 8 cm. 

Here, $PS=PQ=8$ cm and $TU\parallel PQ$ 

⇒ $ST=\dfrac{PS}{2}=\dfrac{8}{2}=4~cm$

And $PQ=TU=8~cm$

⇒ $OT=\dfrac{TU}{2}=\dfrac{8}{2}=4~cm$

Now, Area of triangle OTS 

$=\dfrac{1}{2}~\times base~\times height$

$=\dfrac{1}{2}~\times OT~\times ST$

$=\dfrac{1}{2}~\times 4~\times 4$

$=8~c{{m}^{2}}$

Hence, area of $\Delta OTS$ is $8~c{{m}^{2}}.$

Sample Question 2: ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ (Fig. 9.10). If AQ intersects DC at P, Show that $ar\left( BPC \right)=ar\left( DPQ \right).$

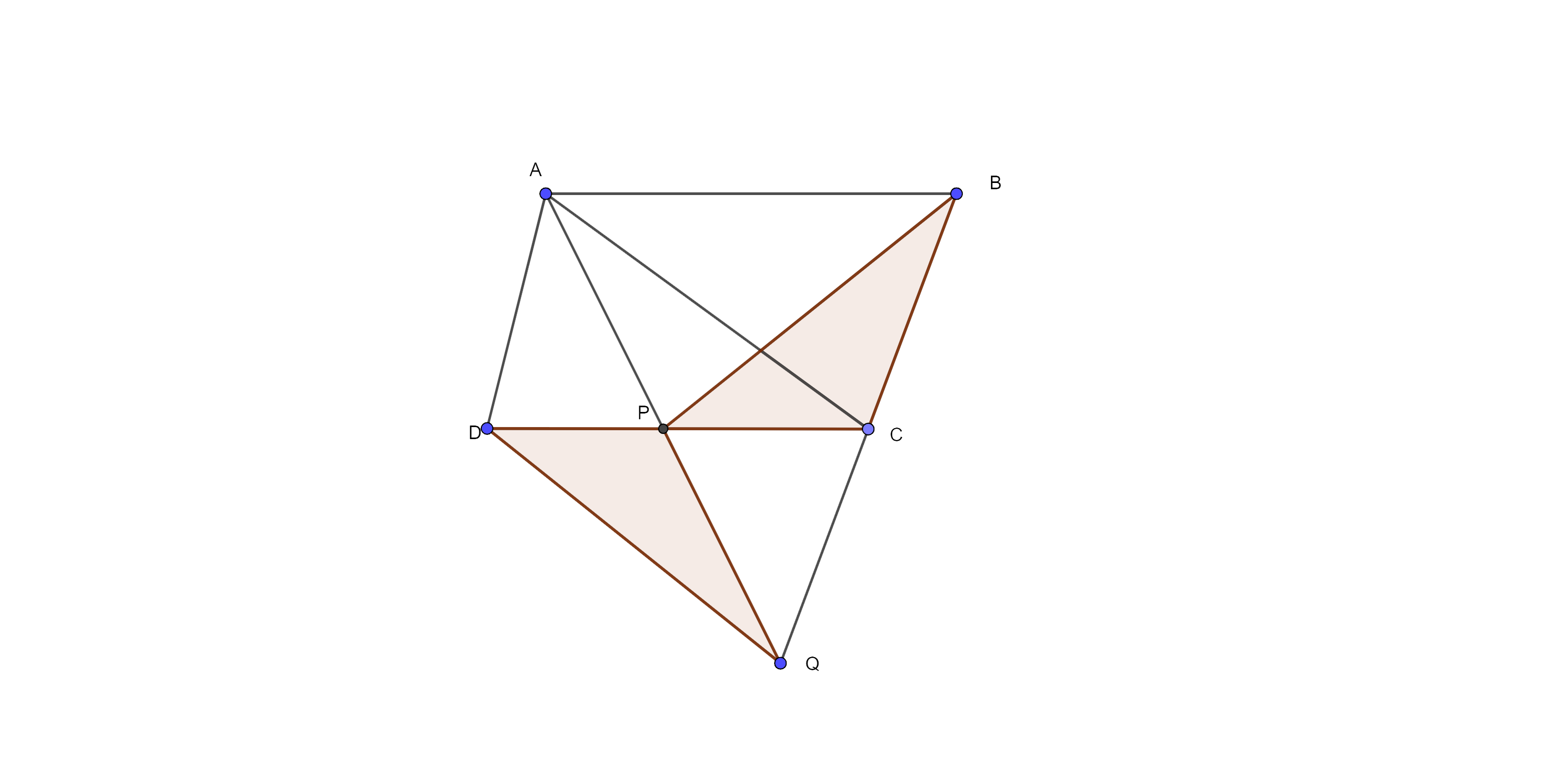
Ans: Here, $\Delta ACP$ and $\Delta BCP$ are on the same base CP and between the same parallel lines. 

Therefore, $ar\left( ACP \right)$ = $ar\left( BCP \right)$ ……….. (i)

Similarly, $ar\left( ADQ \right)$ = $ar\left( ADC \right)$ ……….. (ii)

Now, subtract $ar\left( ADP \right)$ from both sides of eq (ii), we get

⇒ $ar\left( ADQ \right)-ar\left( ADP \right)$  = $ar\left( ADC \right)-ar\left( ADP \right)$ 

⇒ $ar\left( DPQ \right)$  = $ar\left( ACP \right)$ ………..(iii)

From eq (i) and (iii), we get 

⇒ $ar\left( BPC \right)=ar\left( DPQ \right)$

Hence proved.

Exercise 9.3

1. In fig. 9.11. PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and $\mathbf{PA}\parallel \mathbf{QB}\parallel \mathbf{RC}.$ Prove that $\mathbf{ar}\left( \mathbf{PQE} \right)=\mathbf{ar}\left( \mathbf{CFD} \right).$

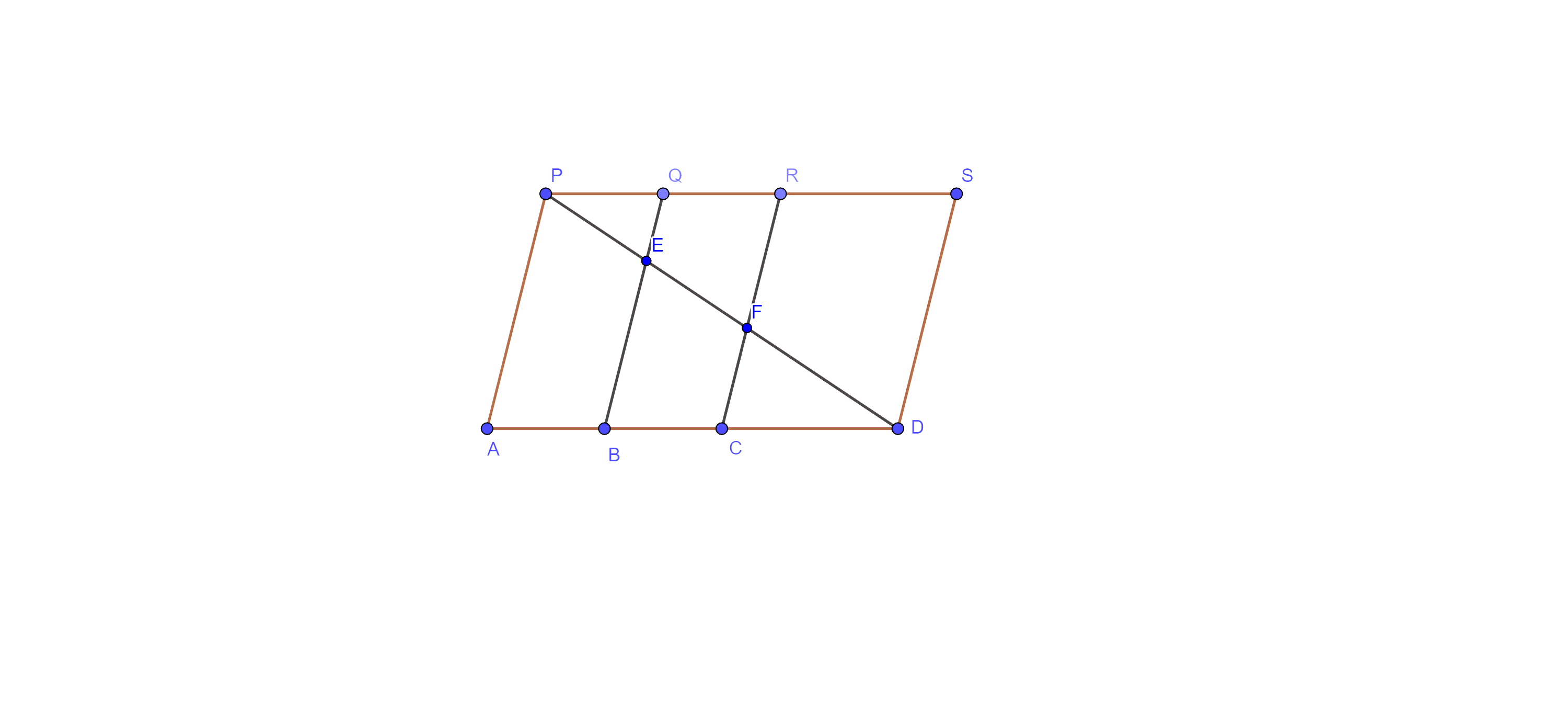
Ans: PSDA is a parallelogram. Points Q and R are taken on PS such that $\text{PQ}=\text{QR}=\text{ }\!\!~\!\!\text{ RS}$ and $\text{PA}\parallel \text{QB}\parallel \text{RC}.$

Now, PS = AD     (Opp.  side of parallelogram)

⇒ $\dfrac{1}{3}\text{ }\!\!~\!\!\text{ PS}=\dfrac{1}{3}\text{ }\!\!~\!\!\text{ AD}$

⇒ $\text{PQ}=\text{CD}$ …………. Eq (i)

In $\Delta \text{PRF},$ Q is the mid- point of PR and  $\text{QE}\parallel \text{RF}$.

Therefore, E is midpoint of PF (by converse of mid- point theorem)

Thus, PE = EF …………. Eq (ii),

Similarly, in $\Delta \text{BDE},$  EF = FD ………… eq (iii)

From eq (ii) and (iii), we get PE = FD

Now, In $\Delta \text{PQE}$ and $\Delta \text{CFD}$

⇒ PQ = CD  (just proved)

⇒ $\angle \text{QPE}=\text{ }\!\!~\!\!\text{ }\angle \text{FDC}$   

⇒ PE = FD (just proved)    

Thus, $\Delta \text{PQE}$ $\cong $ $\Delta \text{CFD}$ by SAS congruency 

Therefore, $\text{ar}\left( \Delta \text{PQE} \right)$$=\text{ar}(\Delta \text{CFD})$  (areas of congruent triangles are equal)

Hence proved.

2. X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See fig. 9.12). Prove that $\mathbf{ar}\left( \mathbf{LZY} \right)=\mathbf{ar}\left( \mathbf{MZYX} \right)$.

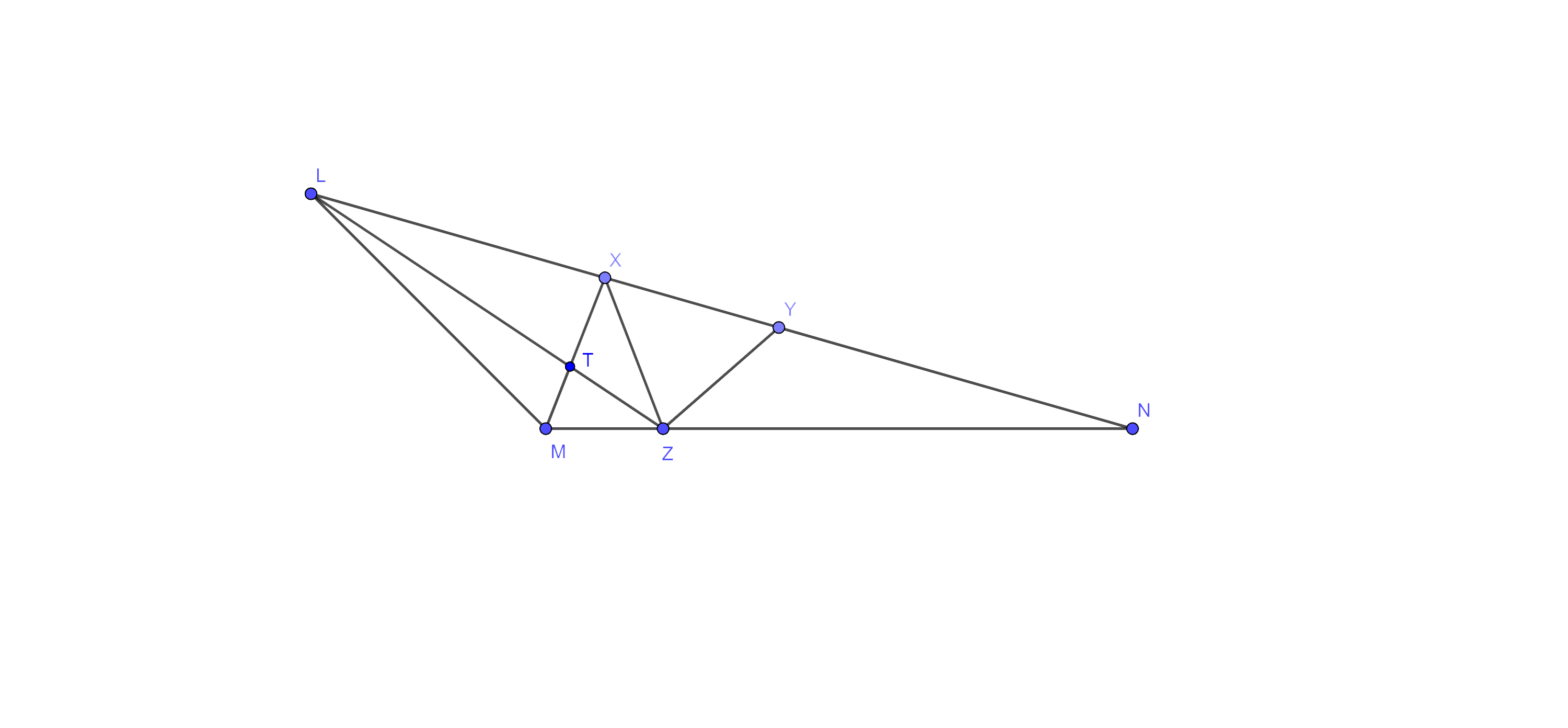
Ans: Given: - X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z.

To prove: - $\text{ar}\left( \text{LZY} \right)=\text{ar}\left( \text{MZYX} \right)$. 

Proof: - here, $\Delta \text{LXZ }\!\!~\!\!\text{ }$ and $\Delta \text{XMZ}$ are on the same base XZ and between the same parallels LM and XZ, we have

⇒ $\text{ar}\left( \Delta \text{LXZ} \right)=\text{ar}\left( \Delta \text{XMZ} \right)$ ………….. eq (i)

Adding $\text{ar}\left( \Delta \text{XYZ} \right)$ to both sides of eq (i), we get

⇒ $\text{ar}\left( \Delta \text{LXZ} \right)+\text{ar}\left( \Delta \text{XYZ} \right)=\text{ar}\left( \Delta \text{XMZ} \right)+\text{ar}\left( \Delta \text{XYZ} \right)$ 

⇒ $\text{ar}\left( \Delta \text{LZY} \right)=\text{ar}\left( \text{MZYX} \right)$

Hence proved.

3. The area of the parallelogram ABCD is $90~\mathbf{c}{{\mathbf{m}}^{2}}$ (see fig. 9.13). 

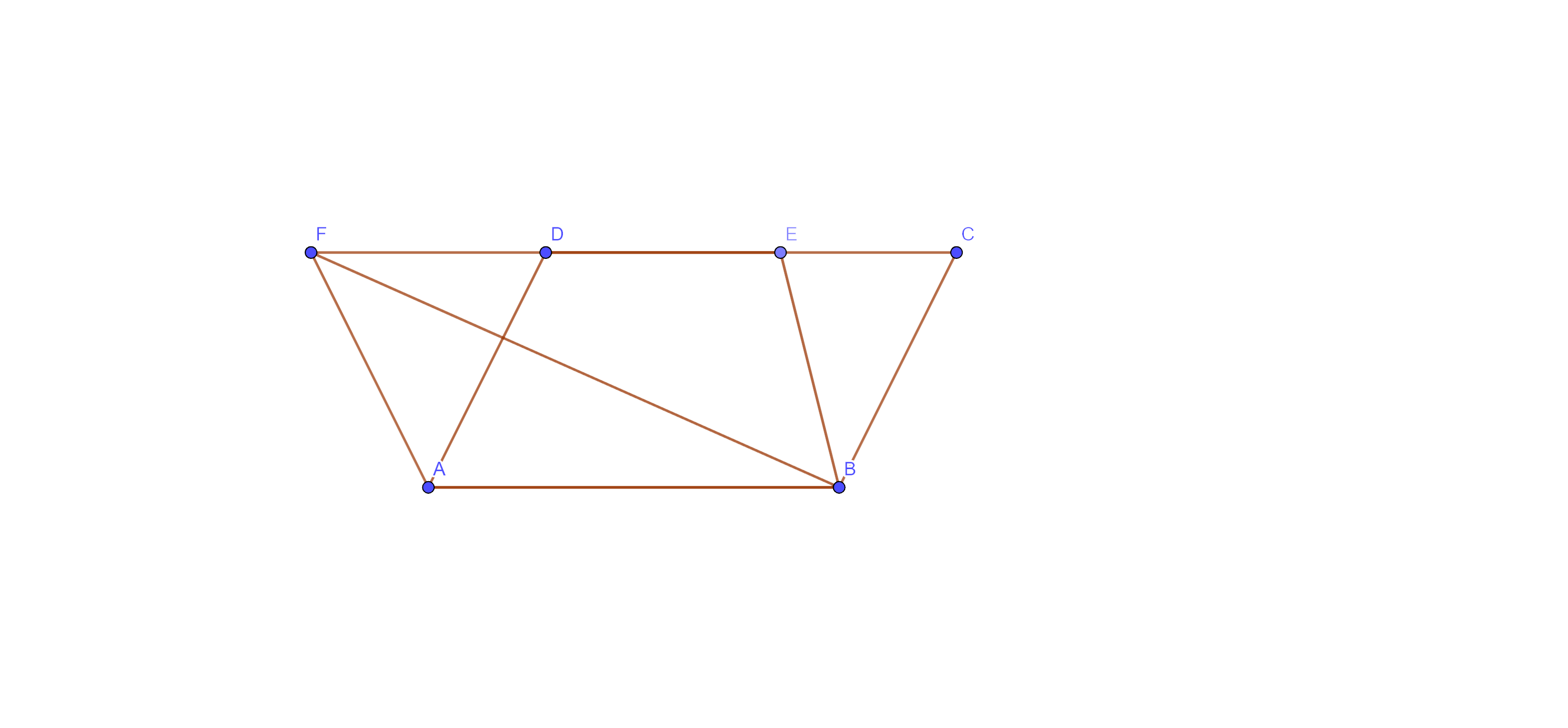
Find 

(i) $\mathbf{ar}\left( \mathbf{ABEF} \right)$

Ans: Ans: Since parallelograms on the same base and between the same parallels are equal in area, so we have

⇒$\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABEF} \right)=\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$ 

Hence, $\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABEF} \right)=\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)=90\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$

(ii) $\mathbf{ar}\left( \mathbf{ABD} \right)$

Ans: $\text{ar}\left( \Delta \text{ABD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$

(a diagonal of a parallelogram divides the parallelogram in two triangles of equal area)

⇒ $\text{ar}\left( \Delta \text{ABD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times 90$

⇒ $\text{ar}\left( \Delta \text{ABD} \right)=45\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}.$

(iii) $\mathbf{ar}\left( \mathbf{BEF} \right)$

Ans: $\text{ar}\left( \Delta \text{BEF} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABEF} \right)$

$=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times 90$

$=45\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$.

4. In $\Delta ~\mathbf{ABC},$ D is the midpoint of AB and P is any on BC. If $\mathbf{CQ}\parallel \mathbf{PD}$ meets AB in Q (fig. 9.14), then prove that $\mathbf{ar}\left( \mathbf{BPQ} \right)=\dfrac{1}{2}~\times \left( \Delta \mathbf{ABC} \right).$

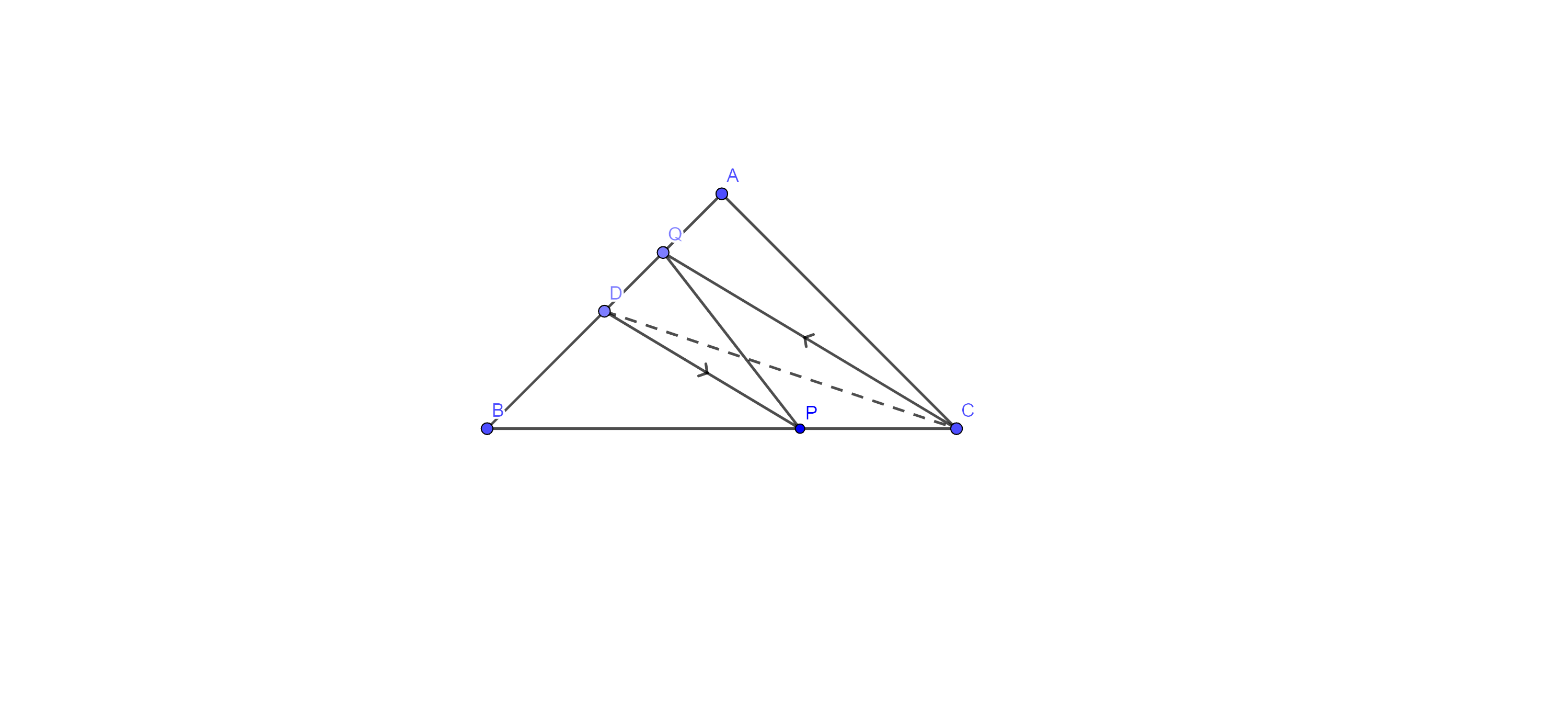
Ans: Given: D is the midpoint of AB and P is any point on BC of $\Delta \text{ABC}$. $\text{CQ}\parallel \text{PD}$ meets AB in Q.

To prove: - $\text{ar}\left( \text{BPQ} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \Delta \text{ABC} \right).$

Proof: - Join CD and we know that median of a triangle divides it into two triangles of equal area, so we have

⇒ $\text{ar}\left( \Delta \text{BCD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \left( \Delta \text{ABC} \right)$ ………… eq (i)

Since, triangles on the same base and between the same parallels are equal in area, so we have

⇒ $\text{ar}\left( \Delta \text{DPQ} \right)=\text{ar}\left( \Delta \text{DPC} \right)$ ………… eq (ii)

Adding $\text{ar}\left( \Delta \text{DPB} \right)$ to both sides of equation (ii)

⇒ $\text{ar}\left( \Delta \text{DPQ} \right)+\text{ar}\left( \Delta \text{DPB} \right)=\text{ar}\left( \Delta \text{DPC} \right)+\text{ar}\left( \Delta \text{DPB} \right)$ ………… eq (ii)

⇒ $\text{ar}\left( \Delta \text{BPQ} \right)=\text{ar}\left( \Delta \text{BCD} \right)$

⇒ $\text{ar}\left( \Delta \text{BPQ} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \Delta \text{ABC} \right)$           (from eq. i)

Hence proved.

5. ABCD is a square. E and F are respectively the midpoint of BC and CD. If R is the midpoint of EF (fig. 9.15). prove that $\mathbf{ar}\left( \Delta \mathbf{AER} \right)=\mathbf{ar}\left( \Delta \mathbf{AFR} \right)$.

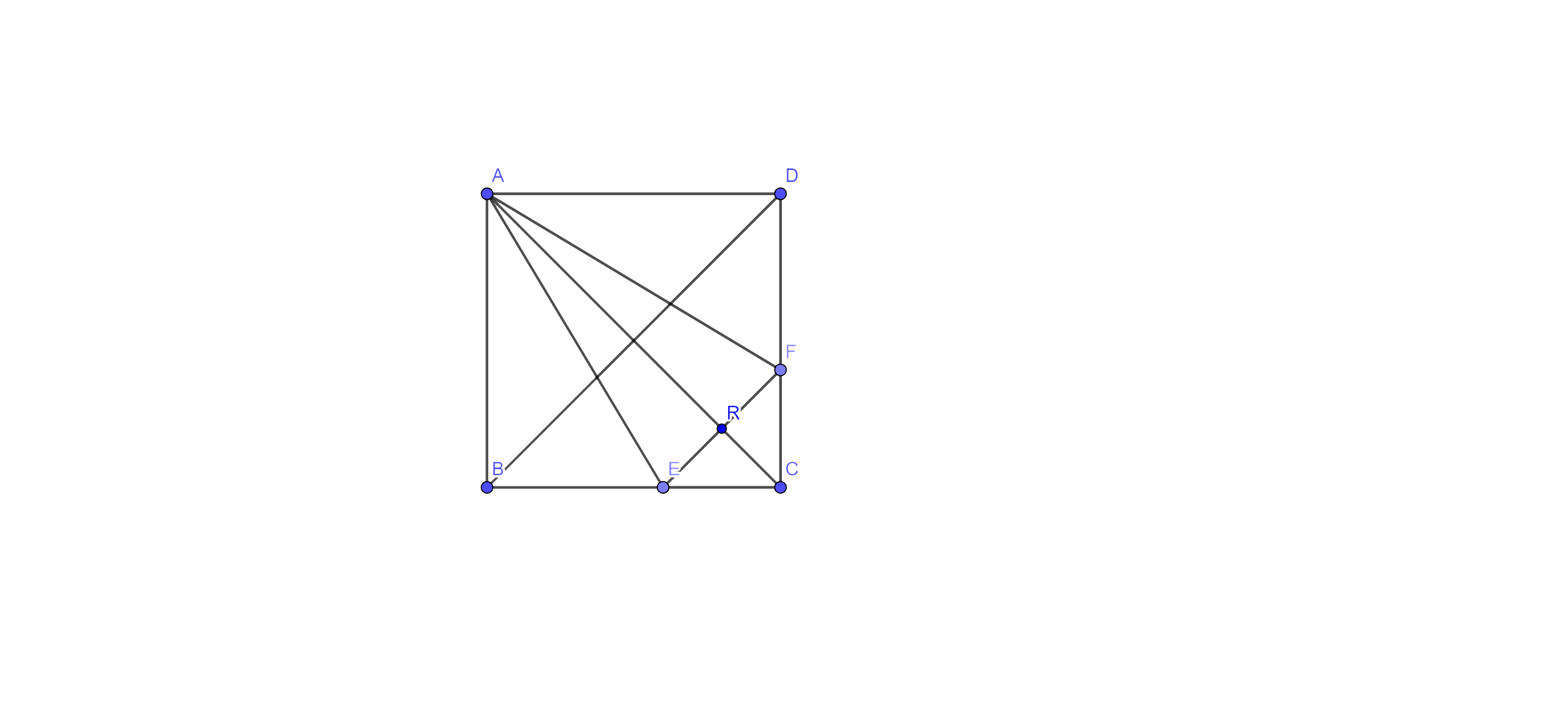
Ans: Given: ABCD is a square. E and F are respectively the mid-points of BC and CD, and R is the midpoint of EF.

To prove: - $\text{ar}\left( \Delta \text{AER} \right)=\text{ar}\left( \Delta \text{AFR} \right)$.

Proof: - In $\Delta \text{ABE}$ and $\Delta \text{ADF}$, we have 

⇒ AB = AD (sides of a square are equal)

⇒ $\angle \text{ABE}=\angle \text{ADF}$    $\text{each} 90{}^\circ $

⇒ $\text{BE}=\text{DF}$      

E is the midpoint of BC and F is the midpoint of CD. Also $\dfrac{1}{2}\text{BC}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ CD}$

Thus, $\Delta \text{ABE}$ $\cong $ $\Delta \text{ADF}$ (by SAS congruence rule)

⇒ AE = AF [ C.P.C.T] ………… (i)

Now, in $\Delta \text{AER}$ and $\Delta \text{AFR}$ , we have 

⇒ AE = AF (just proved)

⇒ ER = RF (R is the midpoint of EF)

And AR = AR (common side)

Hence, as \[\text{ar}\left( \Delta \text{AER} \right)=\text{ar}\left( \Delta \text{AFR} \right)\]   (congruent triangles are equal in area).

6. O is any point on the diagonal PR of a parallelogram PQRS (fig. 9.16). Prove that $\mathbf{ar}\left( \Delta \mathbf{PSO} \right)=\mathbf{ar}\left( \Delta \mathbf{PQO} \right).$

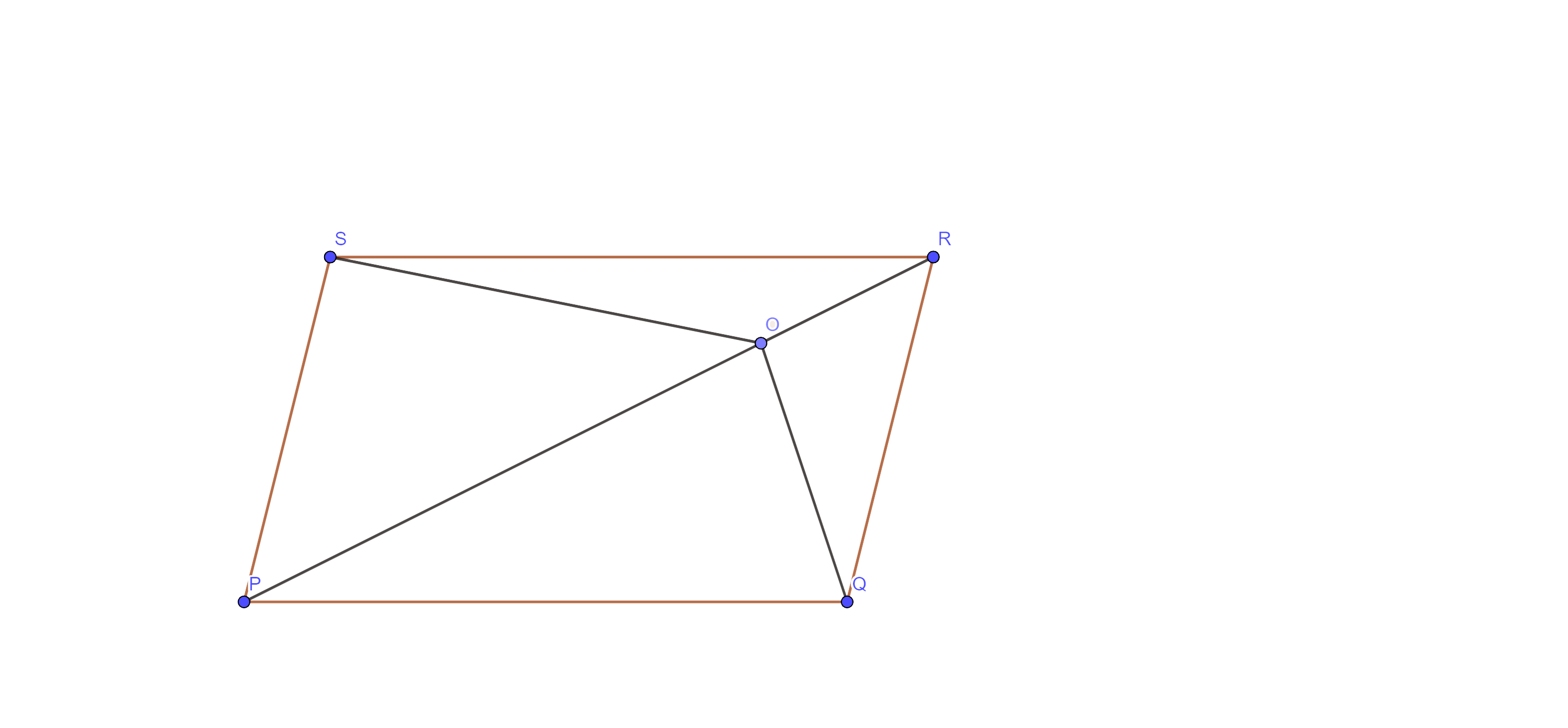
Ans: Given: O is any point on the diagonal PR of a parallelogram PQRS.

To prove: - $\text{ar}\left( \Delta \text{PSO} \right)=\text{ar}\left( \Delta \text{PQO} \right)$

Proof: - Join SQ, bisect the diagonal PM at M. Since Diagonal of a parallelogram bisect each other, so SM = MQ

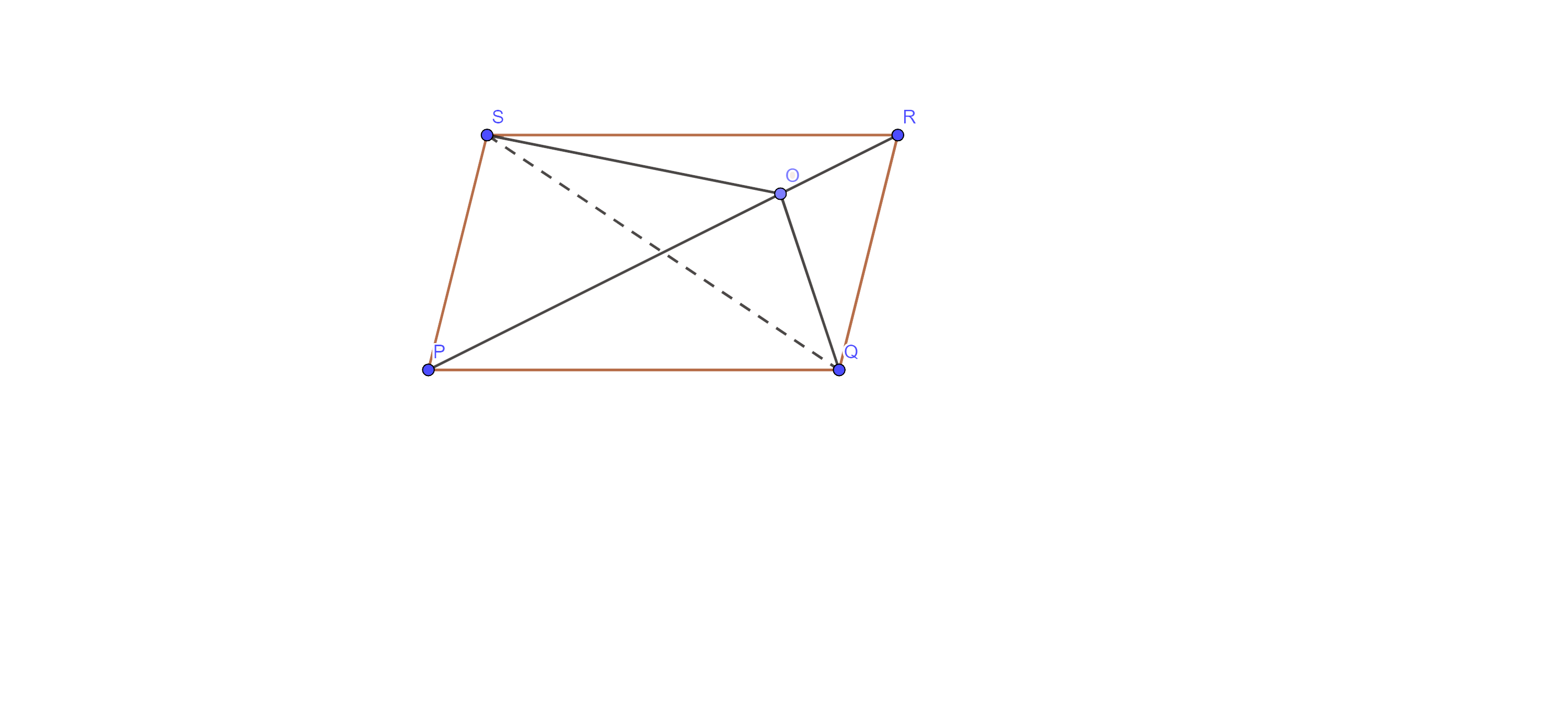
Therefore, PM is a median of $\Delta \text{PQS}$ and we know that the median divides a triangle into two triangles of equal area.

⇒$\text{ar}\left( \Delta \text{PMS} \right)=\text{ar}\left( \Delta \text{PMQ} \right)$ …….. eq (i)   

Again, as OM is the median of $\Delta \text{OSQ}$

⇒$\text{ar}\left( \Delta \text{OMS} \right)=\text{ar}\left( \Delta \text{OMQ} \right)$ …….. eq (ii)   

Now, adding eq (i) and (ii), we get

⇒$\text{ar}\left( \Delta \text{PMS} \right)+\text{ar}\left( \Delta \text{OMS} \right)=\text{ar}\left( \Delta \text{PMQ} \right)+\text{ar}\left( \Delta \text{OMQ} \right)$

⇒$\text{ar}\left( \Delta \text{PSO} \right)=\text{ar}\left( \Delta \text{PQO} \right)$

Hence proved.

7. ABCD is a parallelogram in which BC is produced to E such that CE = BC (fig. 9.17).AE intersects CD at F. If $\text{ar}\left( \text{DFB} \right)=3\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}},$ find the area of the parallelogram ABCD.

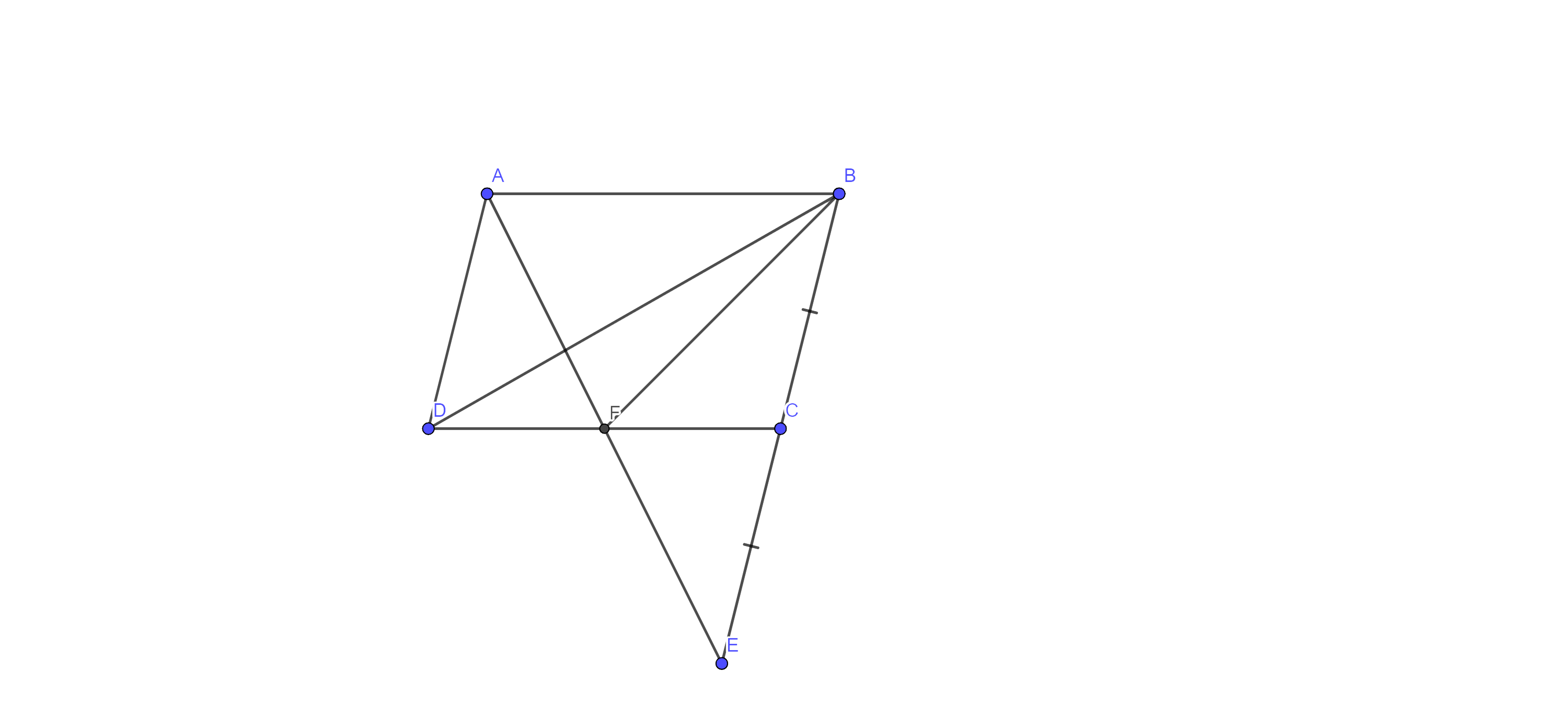
Ans: Here, ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersect CD at F i.e., $\text{ar}\left( \text{DFB} \right)=3\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$

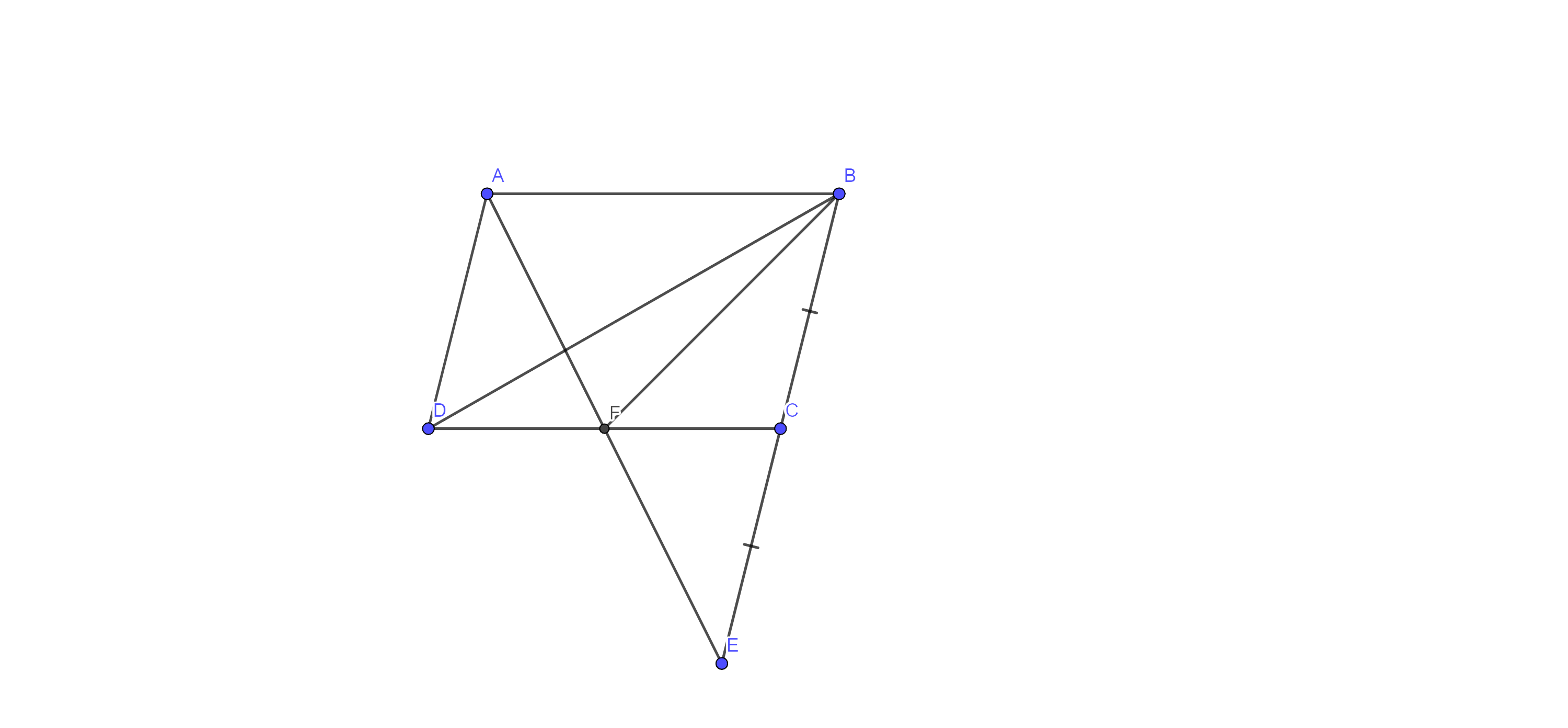
Now, in $\Delta \text{ADF}$ and $\Delta \text{ECF}$

⇒ $\angle \text{A}=\angle \text{E}$        (alternate interior angles)

⇒ $\text{AD}=\text{CE}$         [AD = BC = CE]

⇒ $\angle \text{D}=\angle \text{C}$       (alternate interior angles)

Thus, $\Delta \text{ADF}$ $\cong $ $\Delta \text{ECF}$ by ASA congruence 

Therefore, DF = FC            [C.P.C.T]

Hence, point F is the midpoint of DC. It means BF is the median of $\Delta \text{BDC}.$

⇒$\text{ar}\left( \text{DFB} \right)=\dfrac{1}{2}\times \text{ar}\left( \Delta \text{BDC} \right)$   (median divides a triangle into two equal areas)

⇒$3=\dfrac{1}{2}\times \text{ar}\left( \Delta \text{BDC} \right)$

⇒$\text{ar}\left( \Delta \text{BDC} \right)=6\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$

⇒$2\times \text{ar}\left( \Delta \text{BDC} \right)=2\times 6\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$

⇒$\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)=12\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}$  (The diagonal of a parallelogram divides it into two triangles of equal areas)

Hence, area of the parallelogram ABCD is $12\text{ }\!\!~\!\!\text{ c}{{\text{m}}^{2}}.$

8. In trapezium ABCD. $\mathbf{AB}~\parallel \mathbf{DC}$ and L is the midpoint of BC. Through L, a line $\mathbf{PQ}~\parallel \mathbf{AD}$ has been drawn which meets AB in P and DC produced in Q (fig. 9.18). 

Prove that $\mathbf{ar}\left( \mathbf{ABCD} \right)=\mathbf{ar}\left( \mathbf{APQD} \right)$

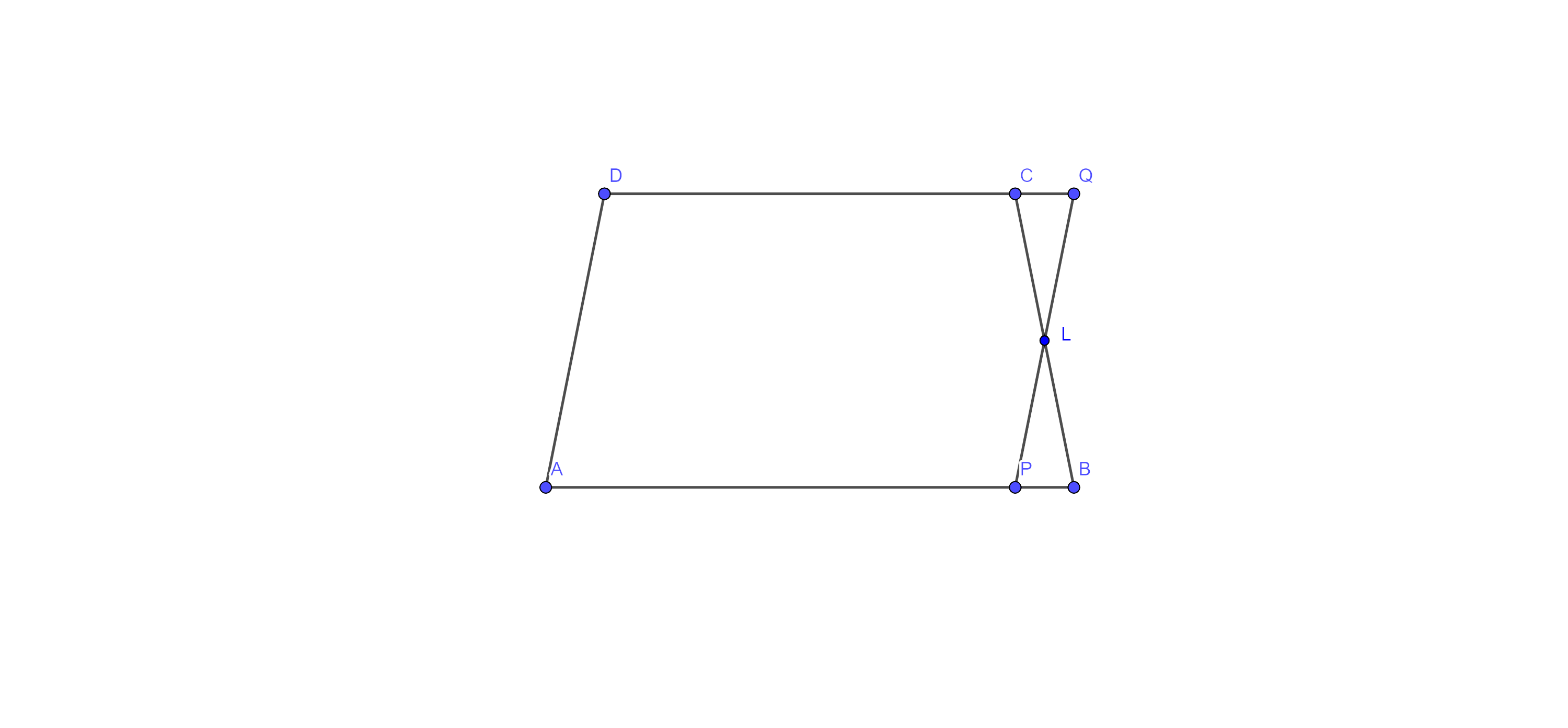
Given: In trapezium ABCD. $\text{AB }\!\!~\!\!\text{ }\parallel \text{DC}$ and L is the midpoint of BC. Through L, a line $\text{PQ }\!\!~\!\!\text{ }\parallel \text{AD}$ has been drawn which meets AB in P and DC produced in Q.

To prove: - $\text{ar}\left( \text{ABCD} \right)=\text{ar}\left( \text{APQD} \right)$

Proof: - here, in $\Delta \text{CLQ}$ and $\Delta \text{BLP}$

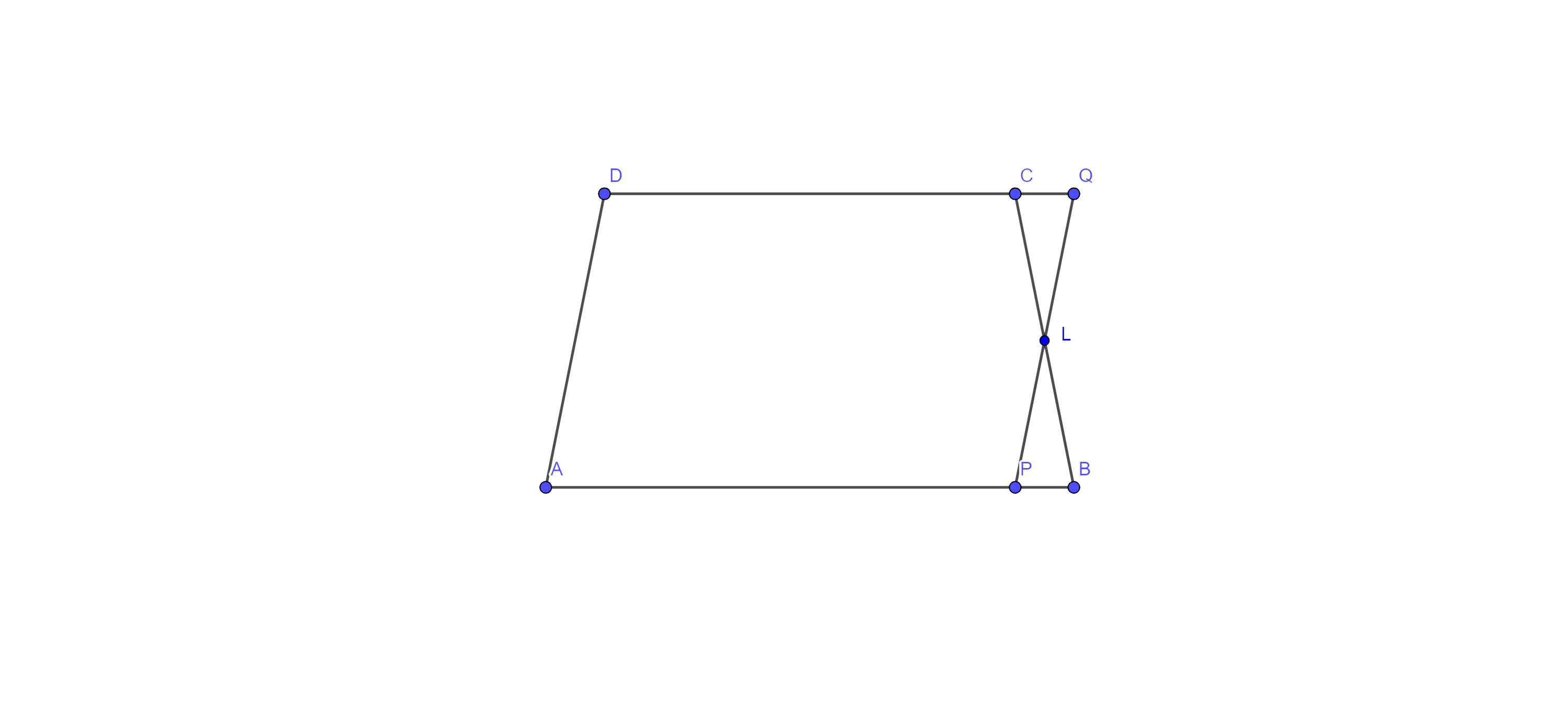
⇒$\angle \text{LCQ}=\angle \text{LBP}$   (alternate interior angles)

⇒$\text{CL}=\text{BL}$               ( L is the midpoint of BC)

⇒$\angle \text{CLQ}=\angle \text{BLP}$     (vertically opposite angles)

Thus, $\Delta \text{CLQ}$ $\cong \Delta \text{BLP}$ by ASA congruence

Therefore, $\text{ar}\left( \Delta \text{CLQ} \right)$ $=\text{ar}\left( \Delta \text{BLP} \right)$   …………. Eq (i)  (areas of two congruent triangles are equal)

Now, adding $\text{ar}\left( \text{APLCD} \right)$ to both sides of eq (i)

⇒ $\text{ar}\left( \Delta \text{CLQ} \right)+\text{ar}\left( \text{APLCD} \right)$  $=\text{ar}\left( \Delta \text{BLP} \right)+\text{ar}\left( \text{APLCD} \right)$ 

⇒ $\text{ar}\left( \text{APQD} \right)$  $=\text{ar}\left( \text{ABCD} \right)$ 

⇒ $\text{ar}\left( \text{ABCD} \right)$  $=\text{ar}\left( \text{APQD} \right)$

Hence proved.

9. If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of a parallelogram formed will be half of the area of the given quadrilateral. Fig (9.19)

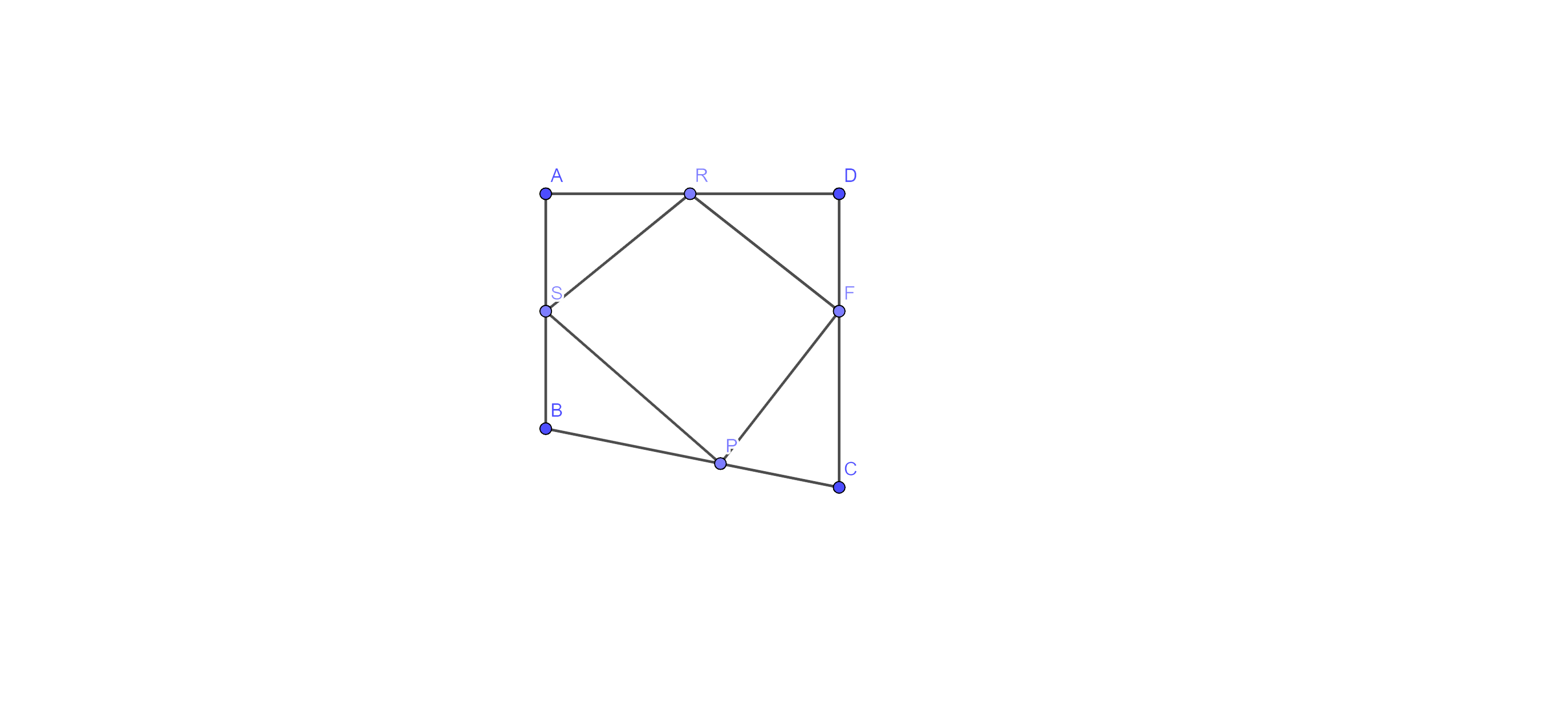
Ans: Given: ABCD is a quadrilateral. Points S, P, F and R the mid points of sides AB, BC, CD and DA respectively.

To prove: - $\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \text{ }\!\!~\!\!\text{ quad}.\text{ }\!\!~\!\!\text{ ABCD} \right)$

Construction: - Join BD and draw perpendicular from A and BD which intersect SR and BD at T and Y respectively.

Proof: - In $\Delta \text{ABD},$ S and R are the mid points of sides AB and AD respectively.

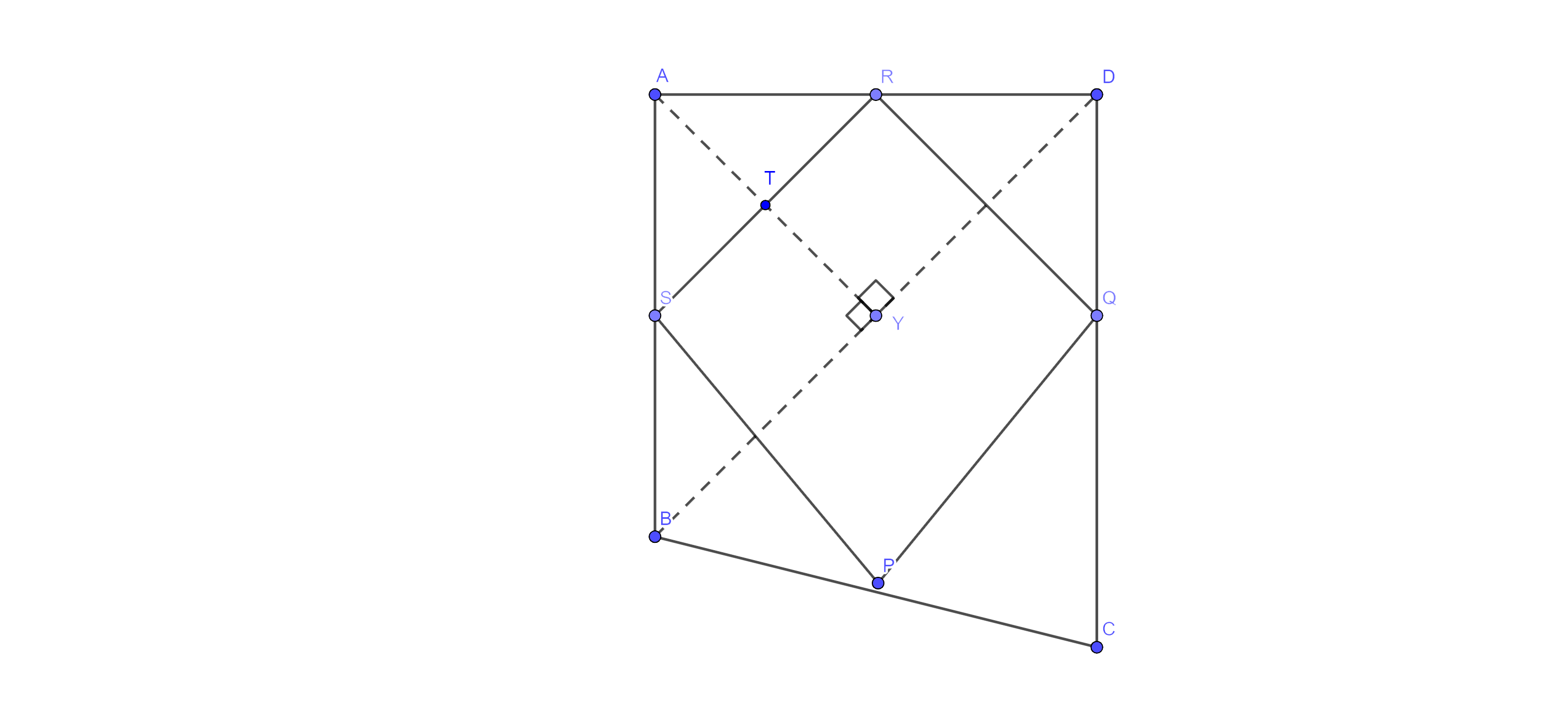
⇒ $\text{SR}\parallel \text{BD}$  and $\text{SR}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ BD }\!\!~\!\!\text{ }$ (by mid-point theorem) … (i)

⇒ $\text{ST}\parallel \text{BY}$

Thus, T is the mid-point of AY.   (Converse of mid-point theorem)

⇒ $\text{AT}=\text{TY}$ or $\text{AT}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ AY}$            …………… (ii)

Now, $\text{ar}\left( \Delta \text{ABD} \right)=\dfrac{1}{2}\times \text{BD}\times \text{AY}$

And $\text{ar}\left( \Delta \text{ASR} \right)=\dfrac{1}{2}\times \text{SR}\times \text{AT}$

$=\dfrac{1}{2}\times \left( \dfrac{1}{2}\text{BD} \right)\times \left( \dfrac{1}{2}\text{ }\!\!~\!\!\text{ AY} \right)$         (from eq(i) and (ii))

$=\dfrac{1}{4}\times \left( \dfrac{1}{2}\times \text{BD}\times \text{AY} \right)$

 ⇒$\text{ar}\left( \Delta \text{ASR} \right)=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{ABD} \right)$ ………… eq (iii)

Similarly, 

⇒$\text{ar}\left( \Delta \text{CPF} \right)=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BCD} \right)$ ………… eq (iv)

⇒$\text{ar}\left( \Delta \text{BSP} \right)=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BAC} \right)$ ………… eq (v)

⇒$\text{ar}\left( \Delta \text{DRF} \right)=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{DAC} \right)$ ………… eq (vi)

Now, adding eq (iii), (iv), (v) and (vi)

⇒$\text{ar}\left( \Delta \text{ASR} \right)+\text{ar}\left( \Delta \text{CPF} \right)+\text{ar}\left( \Delta \text{BSP} \right)+\text{ar}\left( \Delta \text{DRF} \right)$ $=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{ABD} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BCD} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BAC} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{DAC} \right)$ 

⇒$\text{ar}\left( \Delta \text{SR} \right)+\text{ar}\left( \Delta \text{CPF} \right)+\text{ar}\left( \Delta \text{BSP} \right)+\text{ar}\left( \Delta \text{DRF} \right)$$=\dfrac{1}{4}\times \text{ar}\left( \Delta \text{ABD} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BCD} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{BAC} \right)+\dfrac{1}{4}\times \text{ar}\left( \Delta \text{DAC} \right)$

⇒$\text{ar}\left( \text{ABCD} \right)-\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)=\dfrac{1}{4}\times \left[ 2\times \text{ar}\left( \Delta \text{ABCD} \right) \right]$   

⇒$\text{ar}\left( \text{ABCD} \right)-\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)=\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABCD} \right)$

⇒$\text{ar}\left( \text{ABCD} \right)-\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABCD} \right)=\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)$

⇒  $\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABCD} \right)=\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)$

⇒$\text{ar}\left( \parallel \text{gm }\!\!~\!\!\text{ SPFR} \right)=\dfrac{1}{2}\times \text{ar}\left( \Delta \text{ABCD} \right)$

Hence proved.

(E) Long Answer Questions 

Sample Question 1: In Fig. 9.20, ABCD is a parallelogram. Points P and Q on BC trisects BC in three equal parts. 

Prove that $ar\left( APQ \right)=ar\left( DPQ \right)=\dfrac{1}{6}~ar\left( ABCD \right)$

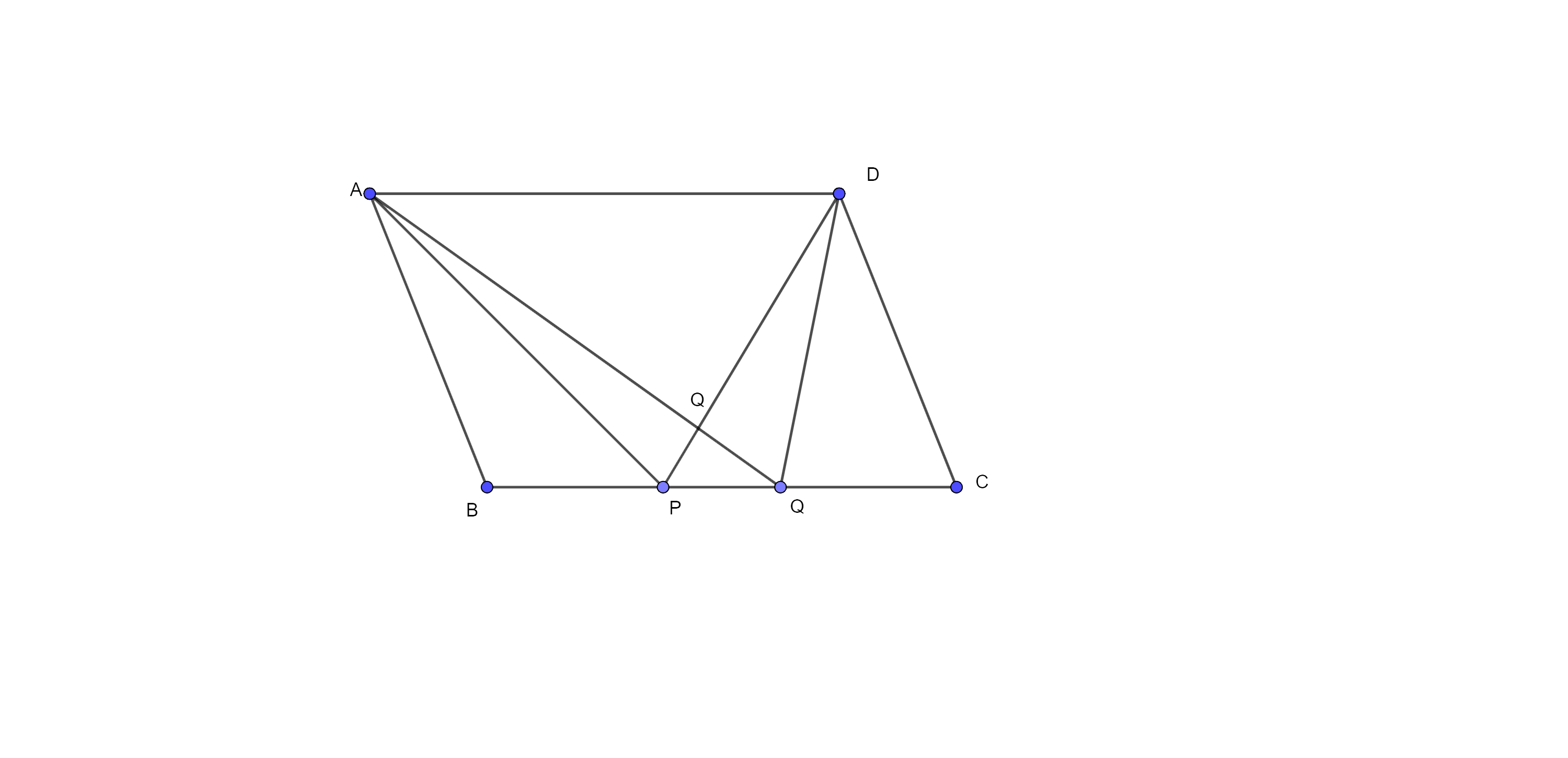
Ans: Given: ABCD is a parallelogram. Points P and Q on BC trisects BC in    three equal parts.

To Prove: $ar\left( APQ \right)=ar\left( DPQ \right)=\dfrac{1}{6}~ar\left( ABCD \right)$

Construction: through P and Q, draw PR and QS parallel to AB.

Proof: here, PQRS is a parallelogram and its base $PQ=\dfrac{1}{3}~BC$.

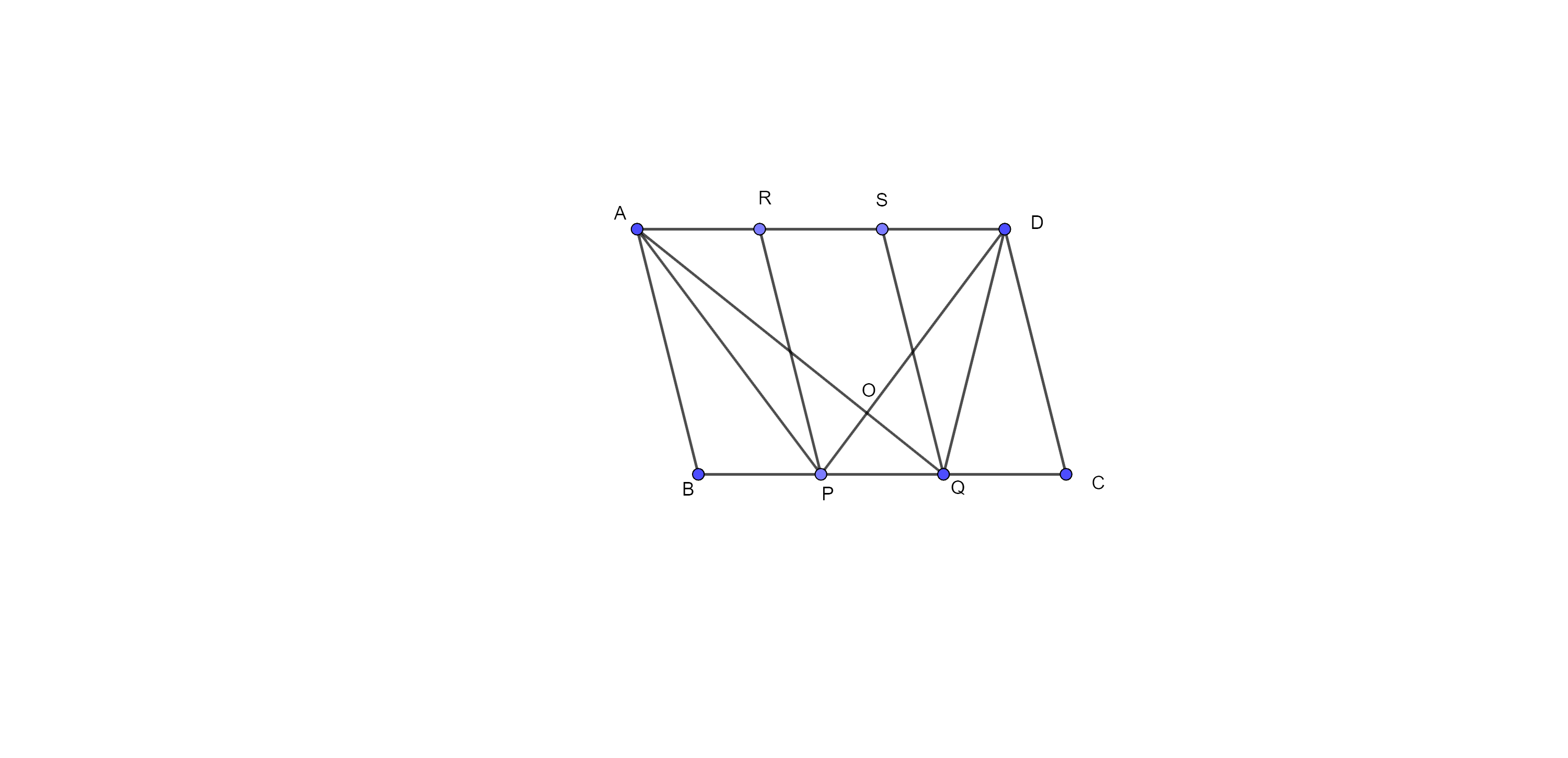
Here, $\Delta APD$ and $\Delta AQD$ are on the same base and between the same   parallel lines.

Therefore,  $ar\left( \Delta APD \right)=ar\left( AQD \right)$…………. (i)

Subtracting  $ar\left( \Delta AOD \right)$ from both sides of eq (i), we get

⇒ $ar\left( \Delta APD \right)-~ar\left( \Delta AOD \right)=ar\left( AQD \right)-~ar\left( \Delta AOD \right)$

⇒ $ar\left( \Delta APO \right)=~ar\left( \Delta OQD \right)$ ……………….. eq (ii)

Now, adding $ar\left( \Delta OPQ \right)$ on both sides in eq (ii), we get

⇒ $ar\left( \Delta APO \right)+ar\left( \Delta OPQ \right)=~ar\left( \Delta OQD \right)+ar\left( \Delta OPQ \right)$

⇒ $ar\left( \Delta APQ \right)=ar\left( \Delta DPQ \right)$ ………………… (iii)

Since $ar\left( \Delta APQ \right)=\dfrac{1}{2}ar\left( PQRS \right)$

Therefore, $ar\left( \Delta DPQ \right)=\dfrac{1}{2}ar\left( PQRS \right)$

Now, $ar\left( PQRS \right)=\dfrac{1}{3}~ar\left( ABCD \right)$

⇒ $\dfrac{1}{2}ar\left( PQRS \right)=\dfrac{1}{2}\times \dfrac{1}{3}~ar\left( ABCD \right)$

⇒ $ar\left( \Delta APQ \right)=ar\left( \Delta DPQ \right)=\dfrac{1}{6}~ar\left( ABCD \right)$

Hence proved.

Sample Question 2: In Fig. 9.22, $l,~m,~n,$ are straight lines such that $l\parallel m$ and$~n$ intersect $l$ at P and $m$ at Q. ABCD is a quadrilateral such that its vertex A is on $l$. The vertices C and D are on m and $AD\parallel n.$ 

Show that $ar\left( ABCQ \right)=ar\left( ABCDP \right).$

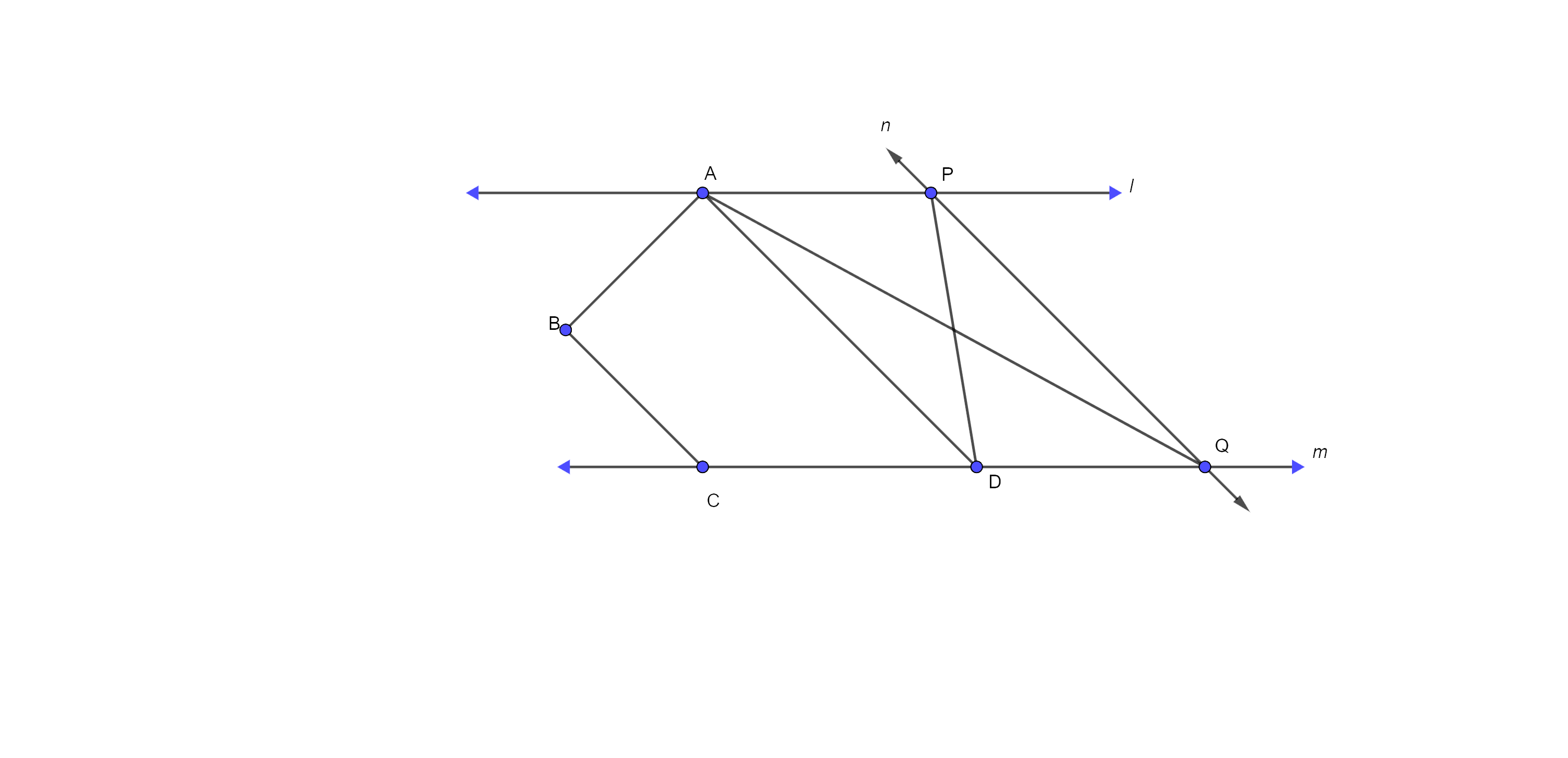
Ans: Here, $\Delta APD$ and $\Delta AQD$ are on the same base AD and also between the same parallel lines.

Therefore, $ar\left( \Delta APD \right)$ = $ar\left( \Delta AQD \right)$ ……….. eq (i)

Now, adding $ar\left( ABCD \right)$ on both sides in eq (i), we get 

⇒ $ar\left( \Delta APD \right)+ar\left( ABCD \right)$  = $ar\left( \Delta AQD \right)+ar\left( ABCD \right)$ 

⇒ $ar\left( ABCDP \right)$  = $ar\left( ABCQ \right)$ 

Hence proved.

Sample Question 3: In Fig. 9.23, $BD\parallel CA$, E is the midpoint of CA and $BD=\dfrac{1}{2}~CA$. Prove that $ar\left( ABC \right)=2~ar\left( DBC \right).$

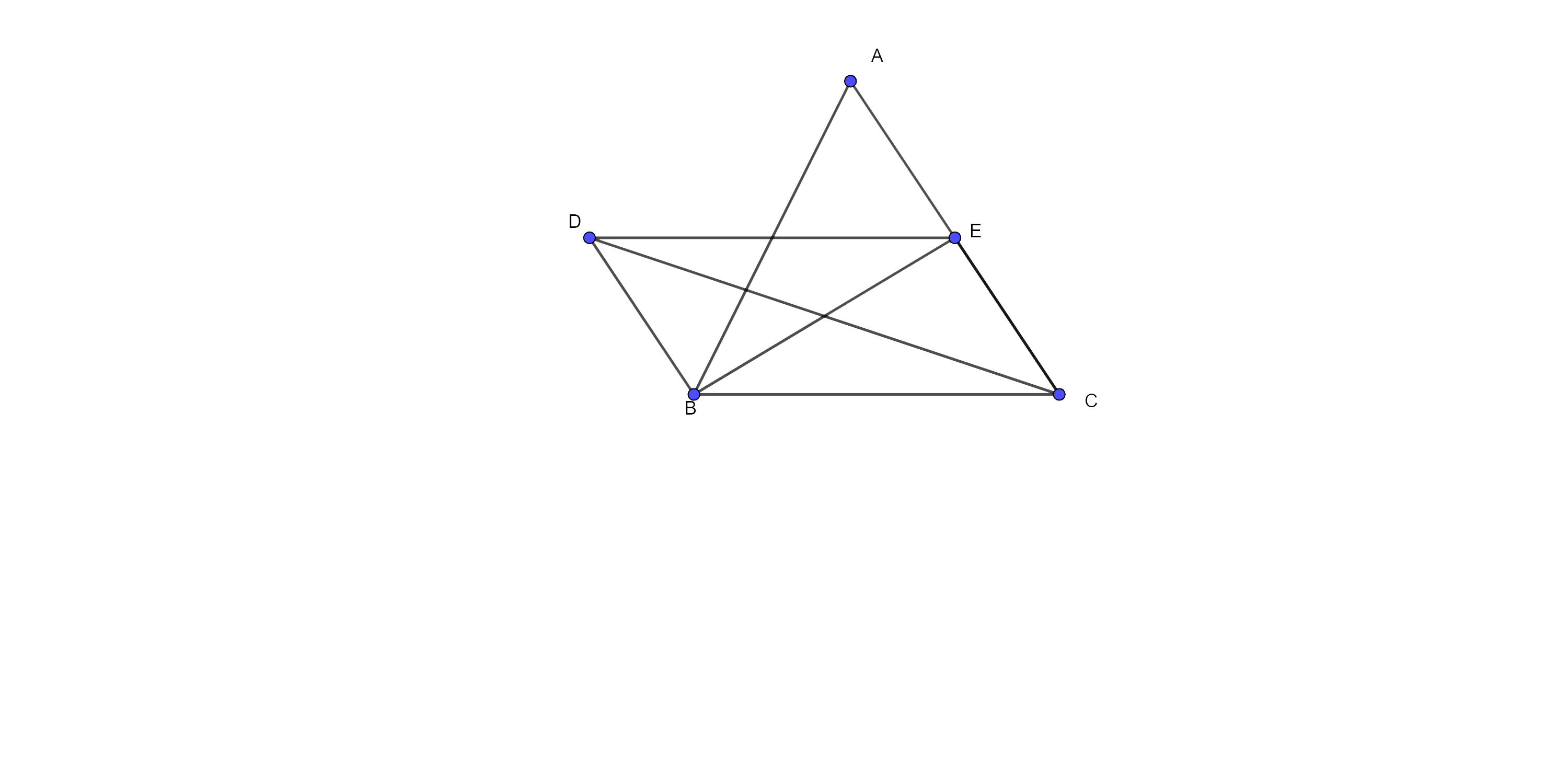
Ans: Given: $BD\parallel CA$, E is the mid point of CA and $BD=\dfrac{1}{2}~CA$

To prove: $ar\left( ABC \right)=2~ar\left( DBC \right)$

Proof: here, $BD\parallel EC$ and $BD=EC$ Thus quadrilateral BCED is a parallelogram. 

⇒ $ar\left( DBC \right)=ar\left( EBC \right)$  ………. (i)

(have the same base BC and between same parallels)

In $\Delta ABC$, BE is the median, 

So, $ar\left( EBC \right)=\dfrac{1}{2}~ar~\left( ABC \right)$  

⇒ $ar\left( ABC \right)=2ar~\left( EBC \right)$  ……… (ii)

From eq (i) and (ii), we get 

⇒ $ar\left( ABC \right)=2ar~\left( DBC \right)$  

Hence proved.

Exercise 9.4

1. A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. 

Prove that $\mathbf{ar}\left( \mathbf{ADF} \right)=\mathbf{ar}\left( \mathbf{ABFC} \right)$

Ans: Given: - A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F.

To prove: - $\text{ar}\left( \text{ADF} \right)=\text{ar}\left( \text{ABFC} \right)$

Proof: - Since ABCD is a parallelogram and diagonal AC divides it into two triangles of equal area, 

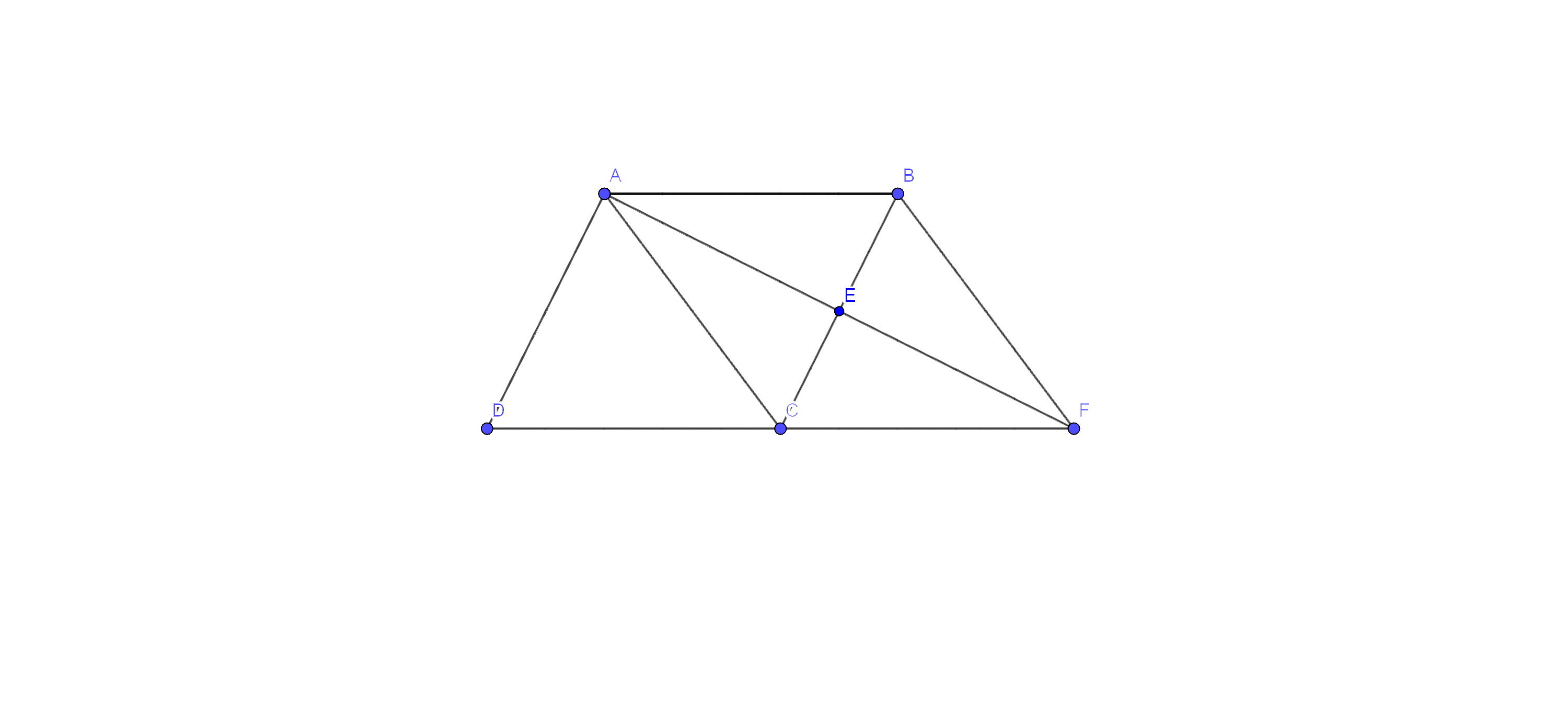
Therefore, 

⇒$\text{ar}\left( \Delta \text{ADC} \right)=\text{ar}\left( \text{ABC} \right)$ ……………. Eq (i)

As, $\text{DC}\parallel \text{AB}$, so $\text{CF}\parallel \text{AB}$

Since triangles on the same base and between the same parallels are equal in area, so we have 

⇒$\text{ar}\left( \Delta \text{ACF} \right)=\text{ar}\left( \text{BCF} \right)$ ……………. Eq (ii)

Adding eq (i) and (2), we get

⇒$\text{ar}\left( \Delta \text{ADC} \right)+\text{ar}\left( \Delta \text{ACF} \right)=\text{ar}\left( \text{ABC} \right)+\text{ar}\left( \text{BCF} \right)$

⇒$\text{ar}\left( \Delta \text{ADF} \right)=\text{ar}\left( \text{ABFC} \right)$

Hence proved.

2. The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.

Ans: AC is a diagonal of the $\parallel \text{gm}$ ABCD

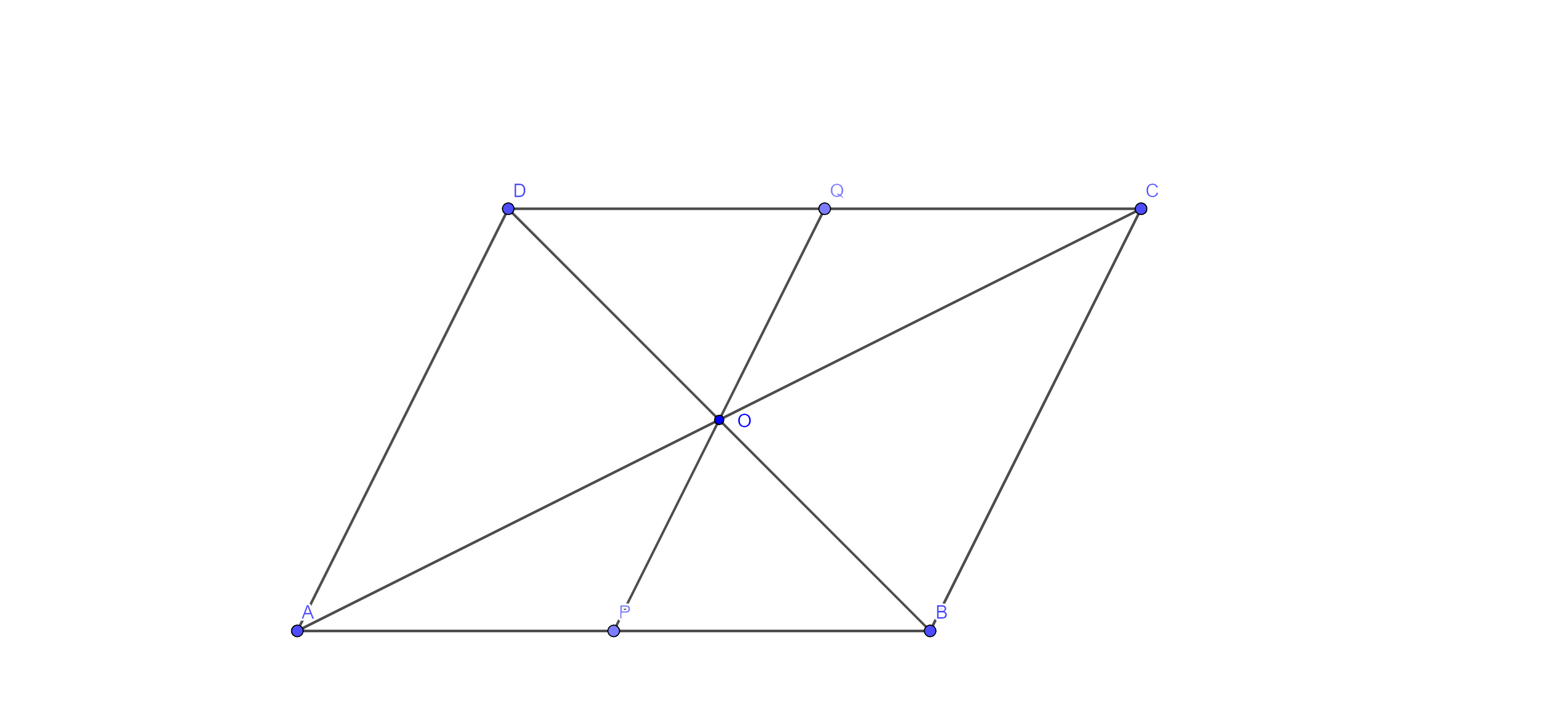
$\therefore \text{ar}\left( \Delta \text{ACD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$ ………. Eq (i)

Now, in $\Delta \text{AOP}$ and $\Delta \text{COQ}$

⇒ AO = CO           (diagonals of a $\parallel \text{gm}$ bisect each other)

⇒ $\angle \text{AOP}=\text{ }\!\!~\!\!\text{ }\angle \text{COQ}$    (vertically opp. angles)

And   $\angle \text{OAP}=\text{ }\!\!~\!\!\text{ }\angle \text{OCQ}$   (alternate interior angle)

Thus, $\Delta \text{AOP}$ $\cong $ $\Delta \text{COQ}$  by ASA congruence rule

Hence, $\text{ar}\left( \Delta \text{AOP} \right)$ $=\text{ar}\left( \Delta \text{COQ} \right)$  (congruency Area axiom)………….. eq (ii)

Adding $\text{ar}\left( \text{quad}.\text{ }\!\!~\!\!\text{ AOQD} \right)$ to both sides of eq (ii), we get

⇒ $\text{ar}\left( \Delta \text{AOP} \right)+\text{ar}\left( \text{quad}.\text{ }\!\!~\!\!\text{ AOQD} \right)$ $=\text{ar}\left( \Delta \text{COQ} \right)+\text{ar}\left( \text{quad}.\text{ }\!\!~\!\!\text{ AOQD} \right)$   

⇒ $\text{ar}\left( \text{quad}.\text{ }\!\!~\!\!\text{ APQD} \right)$ $=\text{ar}\left( \Delta \text{ACD} \right)$ …………… eq (iii)

But, $\text{ar}\left( \Delta \text{ACD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$   (from eq (i))

⇒ $\text{ar}\left( \text{quad}.\text{ }\!\!~\!\!\text{ APQD} \right)=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ ar}\left( \parallel \text{gm }\!\!~\!\!\text{ ABCD} \right)$    

So, PQ divides the parallelogram into two parts of equal area.

Hence proved. 

3. The medians BE and CF of a triangle ABC intersect at G. Prove that the area of $\Delta \mathbf{GBC}$ = area of the quadrilateral AFGE.

Ans: Given: The medians BE and CF of a triangle ABC intersect at G

To prove: - The area of $\Delta \text{GBC}$ = area of the quadrilateral AFGE

Proof :- here, we have

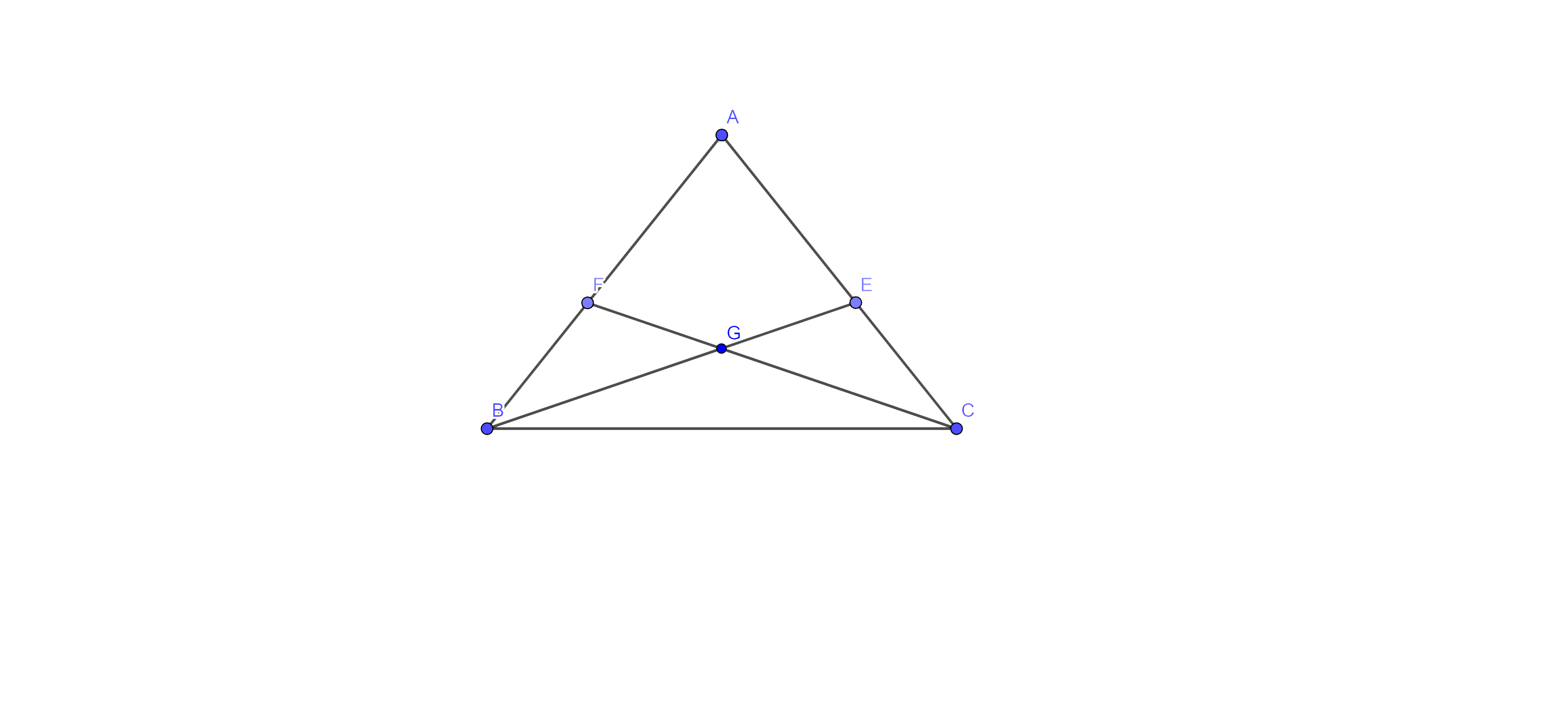
Since median CF divides a triangle into two triangles of equal area, so we have 

⇒ $\text{ar}\left( \Delta \text{BCF} \right)=\text{ar}\left( \Delta \text{ACF} \right)$

⇒ $\text{ar}\left( \Delta \text{GBF} \right)+\text{ar}\left( \text{GBC} \right)=\text{ar}\left( \Delta \text{AFGE} \right)+\text{ar}\left( \Delta \text{GCE} \right)$ ……. (i)

Now, median BE divides a triangle into two triangles of equal area, so we have 

⇒ $\text{ar}\left( \Delta \text{ABE} \right)=\text{ar}\left( \Delta \text{BCE} \right)$

⇒ $\text{ar}\left( \Delta \text{GBF} \right)+\text{ar}\left( \Delta \text{AFGE} \right)=\text{ar}\left( \Delta \text{GCE} \right)+\text{ar}\left( \Delta \text{GBC} \right)$ ……. Eq (ii)

Subtracting eq(ii) from (i), we get

⇒ $\text{ar}\left( \text{GBC} \right)-\text{ar}\left( \Delta \text{AFGE} \right)=\text{ar}\left( \Delta \text{AFGE} \right)-\text{ar}\left( \Delta \text{GBC} \right)$

⇒ $\text{ar}\left( \text{GBC} \right)+\text{ar}\left( \Delta \text{GBC} \right)=\text{ar}\left( \Delta \text{AFGE} \right)+\text{ar}\left( \Delta \text{AFGE} \right)$

⇒ $2\times \text{ar}\left( \text{GBC} \right)=2\times \text{ar}\left( \Delta \text{AFGE} \right)$

⇒ $\text{ar}\left( \text{GBC} \right)=\text{ar}\left( \Delta \text{AFGE} \right)$

Hence proved.

4. In Fig. 9.24, $\text{CD}\parallel \text{AE}$ and $\text{CY}\parallel \text{BA}$. Prove that $\text{ar}\left( \text{CBX} \right)=\text{ar}\left( \text{AXY} \right)$.

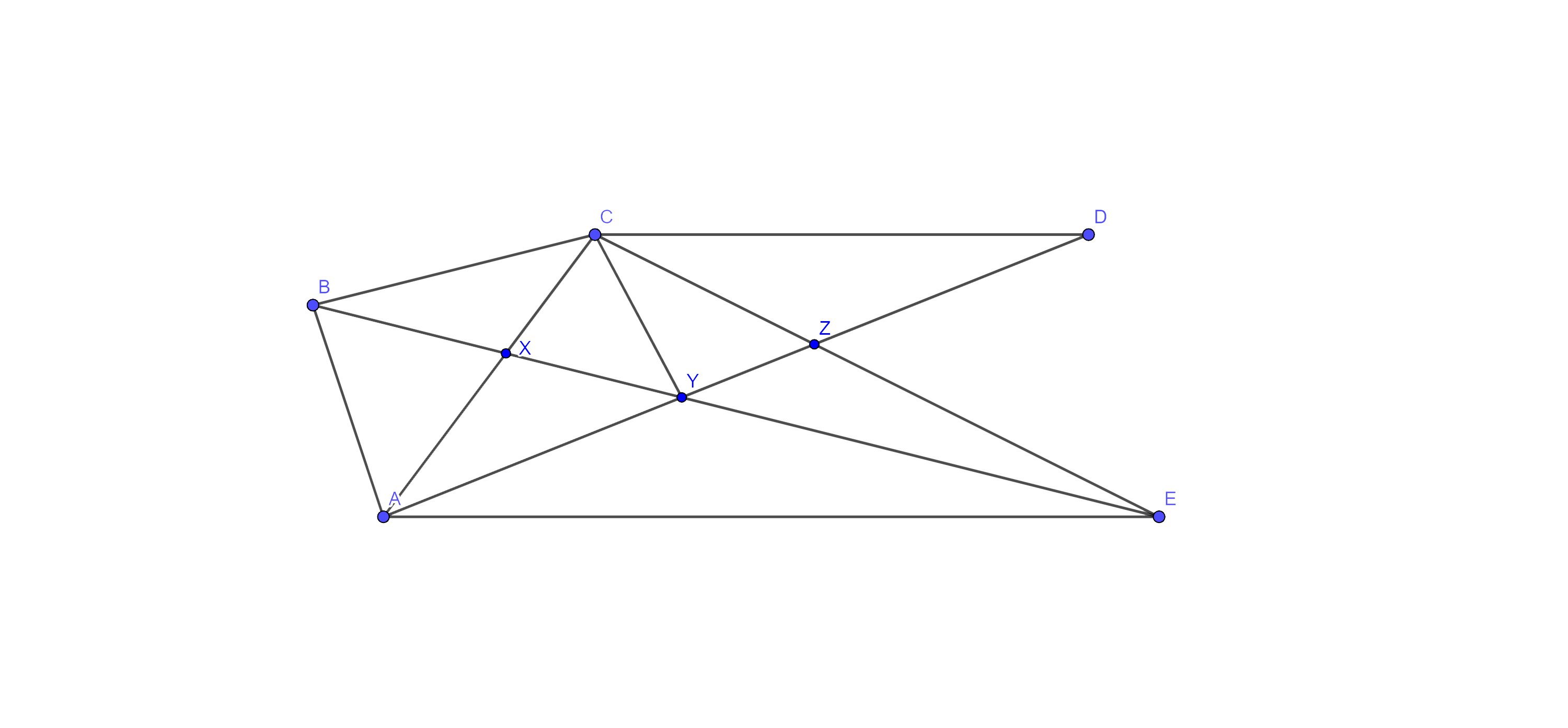
Ans: Given: - $\text{CD}\parallel \text{AE}$ and $\text{CY}\parallel \text{BA}$

To prove: - $\text{ar}\left( \text{CBX} \right)=\text{ar}\left( \text{AXY} \right)$

Proof: - here we have $\text{CD}\parallel \text{AE}$ and $\text{CY}\parallel \text{BA}$

Since triangles on the same base and between the same parallels are equal in area, so we have 

⇒ $\text{ar}\left( \Delta \text{ABC} \right)=\text{ar}\left( \Delta \text{ABY} \right)$ 

⇒ $\text{ar}\left( \Delta \text{CBX} \right)+\text{ar}\left( \Delta \text{ABX} \right)=\text{ar}\left( \Delta \text{ABX} \right)+\text{ar}\left( \Delta \text{AXY} \right)$

⇒ $\text{ar}\left( \Delta \text{CBX} \right)=\text{ar}\left( \Delta \text{AXY} \right)$

Hence proved.

5. ABCD is a trapezium in which $\mathbf{AB}\parallel \mathbf{DC},$ DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that $\mathbf{ar}\left( \mathbf{DCYX} \right)=\dfrac{7}{9}~\mathbf{ar}\left( \mathbf{XYBA} \right)$.

Ans: Given: - ABCD is a trapezium in which $\text{AB}\parallel \text{DC},$ DC = 30 cm and AB = 50 cm. X and Y are the mid-points of AD and BC respectively.

To prove: - $\text{ar}\left( \text{DCYX} \right)=\dfrac{7}{9}\text{ }\!\!~\!\!\text{ ar}\left( \text{XYBA} \right)$

Proof: - Join DY and extended DY intersecting AB produced at M. 

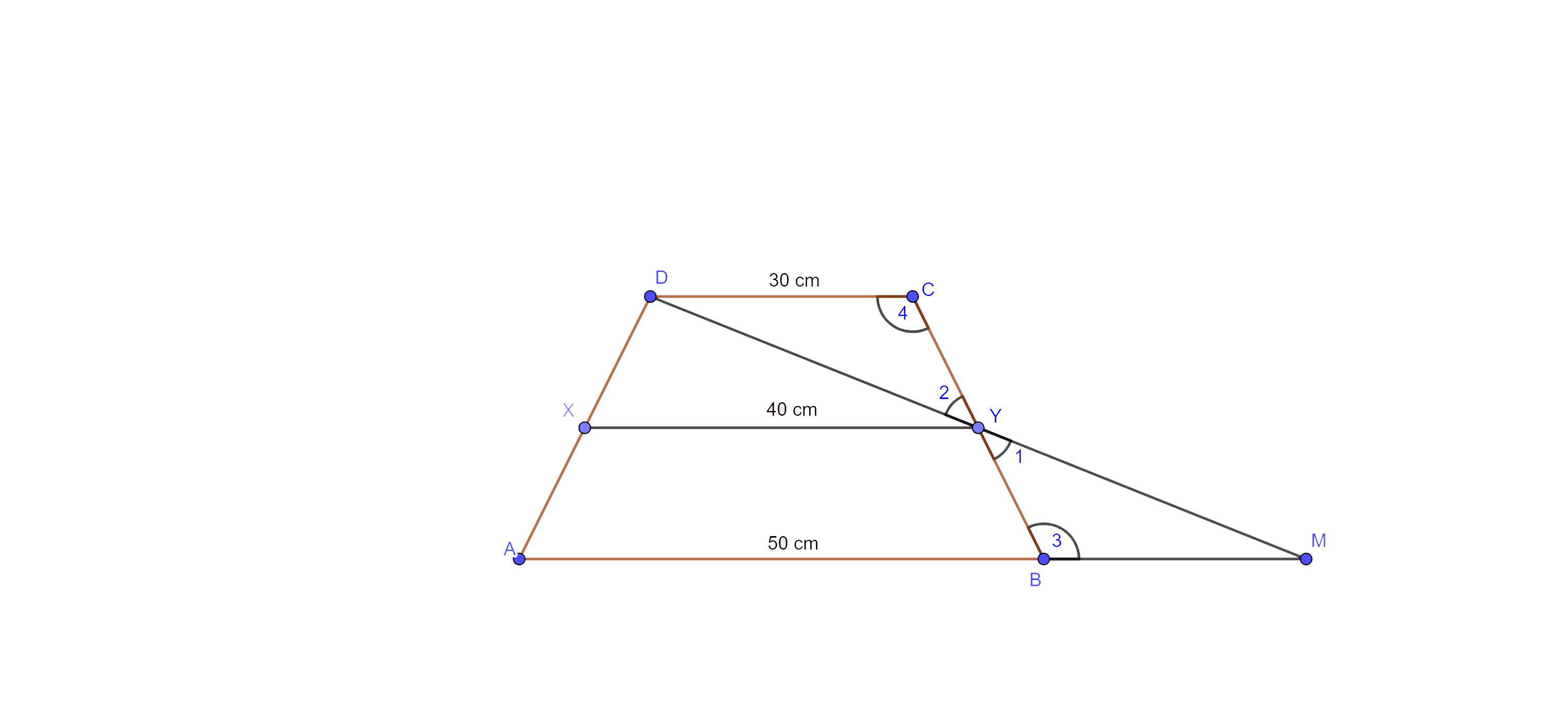
Now, In $\Delta \text{MBY}$ and $\Delta \text{DCY}$, we have 

⇒ $\angle 1=\angle 2$          (vertically opposite angles)

⇒ $\angle 3=\angle 4$            ($\because \text{AB}\parallel \text{DC}$, alternate interior angles)

And $\text{BY}=\text{CY}$          ($\because \text{Y}$ is the midpoint of BC)

$\therefore \text{ }\!\!~\!\!\text{ }\Delta \text{MBY}\cong \Delta \text{DCY}$ (by ASA congruency rule)

So, MB = DC = 30 cm  {CPCT}

In $\Delta \text{ADM},$ we have $\text{XY}=\dfrac{1}{2}\text{ }\!\!~\!\!\text{ AM}=\dfrac{1}{2}\times 80\text{ }\!\!~\!\!\text{ cm}=40\text{ }\!\!~\!\!\text{ cm}$

Now, $\text{AB}\parallel \text{XY}\parallel \text{DC}$ and X and Y are the mid-points of AD and BC, so the height of trapezium DCYX and XYBA are equal. Let the equal height be h cm.

⇒ $\dfrac{\text{ar}\left( \text{DCYX} \right)}{\text{ar}\left( \text{XYBA} \right)}=\dfrac{\dfrac{1}{2}\left( 30+40 \right)\times \text{h}}{\dfrac{1}{2}\left( 40+50 \right)\times \text{h}}$

⇒ $\dfrac{\text{ar}\left( \text{DCYX} \right)}{\text{ar}\left( \text{XYBA} \right)}$ $=\dfrac{70}{90}$

⇒ $\dfrac{\text{ar}\left( \text{DCYX} \right)}{\text{ar}\left( \text{XYBA} \right)}$ $=\dfrac{7}{9}$

⇒ $\text{ar}\left( \text{DCYX} \right)$ $=\dfrac{7}{9}\times \text{ar}\left( \text{XYBA} \right)$

Hence Proved.

6. In $\Delta \mathbf{ABC}$, if L and M are the points on AB and AC, respectively such that $\mathbf{LM}\parallel \mathbf{BC}.$ Prove that $\mathbf{ar}\left( \mathbf{LOB} \right)=\mathbf{ar}\left( \mathbf{MOC} \right).$

Ans: Given: - In $\Delta \text{ABC}$, if L and M are the points on AB and AC, respectively such that $\text{LM}\parallel \text{BC}.$

To prove: -  $\text{ar}\left( \text{LOB} \right)=\text{ar}\left( \text{MOC} \right)$

Proof: - Since triangles on the same base and between the same parallels are equal in area, So we have

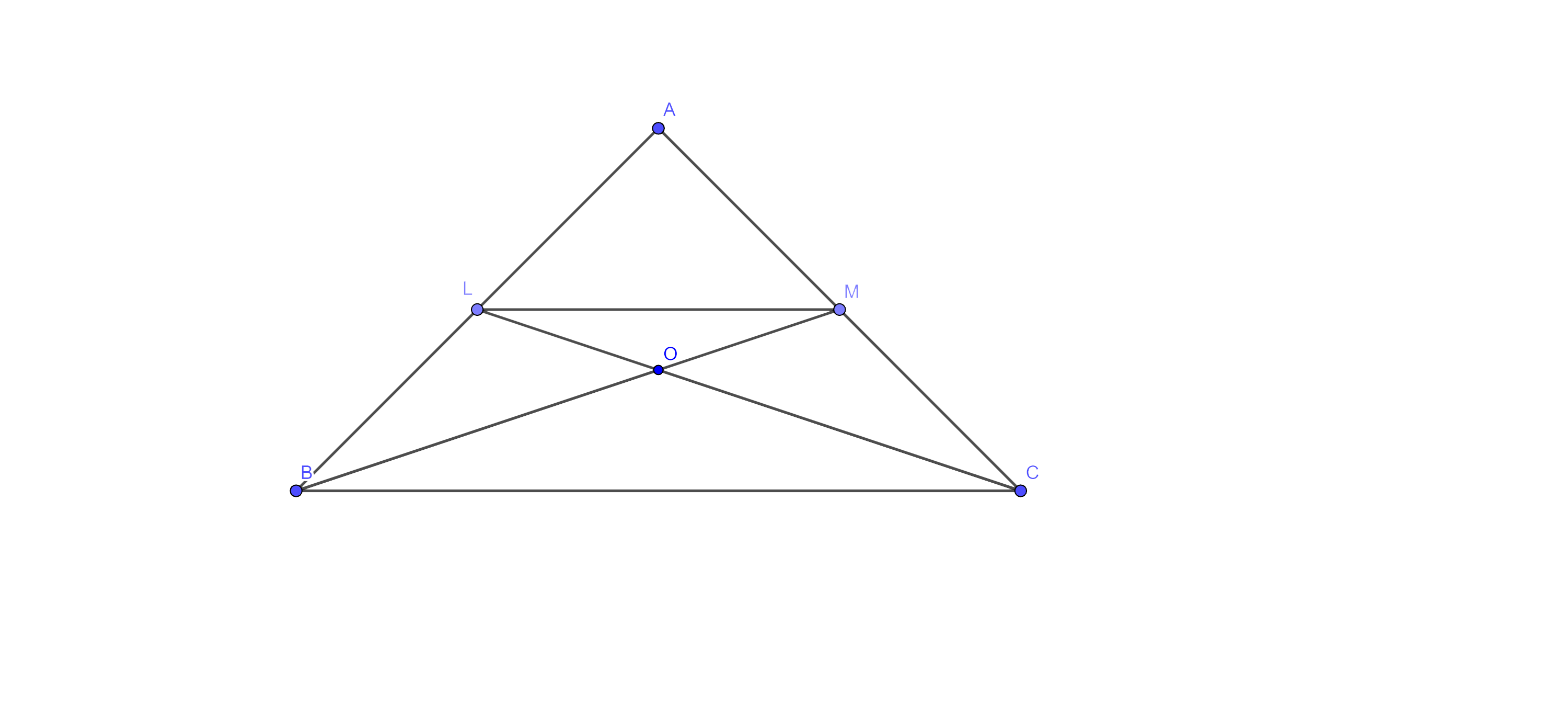
⇒ $\text{ar}\left( \Delta \text{LBM} \right)=\text{ar}\left( \Delta \text{LCM} \right)$

$[\left( \Delta \text{LBM} \right)\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }\left( \Delta \text{LCM} \right)$ are on the same base LM and between the same parallels LM and BC]

⇒ $\text{ar}\left( \Delta \text{LOM} \right)+\text{ar}\left( \Delta \text{LOB} \right)=\text{ar}\left( \Delta \text{LOM} \right)+\text{ar}\left( \text{MOC} \right)$

⇒ $\text{ar}\left( \Delta \text{LOB} \right)=\text{ar}\left( \text{MOC} \right)$

Hence proved.

7. In fig. 9.25, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that $\mathbf{ar}\left( \mathbf{ABCDE} \right)=\mathbf{ar}\left( \mathbf{APQ} \right).$

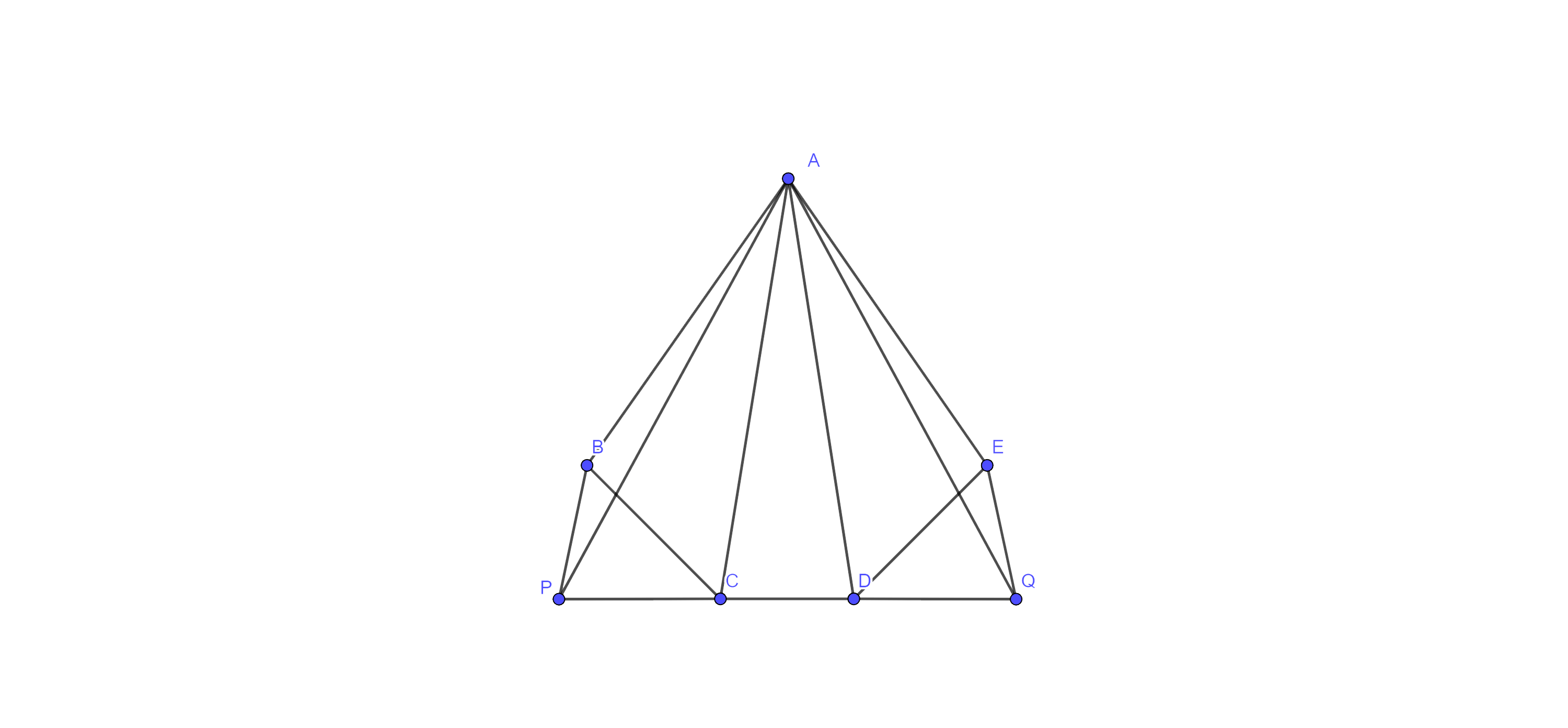
Ans: Given:- ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q.

To prove: - $\text{ar}\left( \text{ABCDE} \right)=\text{ar}\left( \text{APQ} \right).$

Proof: - here, $\text{BP}\parallel \text{AC}$ and $\text{AD}\parallel \text{EQ}$

Since, triangles on the same base and between the same parallels are equal in area.

⇒ $\text{ar}\left( \Delta \text{ABC} \right)=\text{ar}\left( \Delta \text{APC} \right)$ …………. Eq (i)

And $\text{ar}\left( \Delta \text{ADE} \right)=\text{ar}\left( \Delta \text{ADQ} \right)$ …………. Eq (ii)

Adding eq(i) and (ii), we get

⇒ $\text{ar}\left( \Delta \text{ABC} \right)+\text{ar}\left( \Delta \text{ADE} \right)=\text{ar}\left( \Delta \text{APC} \right)+\text{ar}\left( \Delta \text{ADQ} \right)$

Adding $\text{ar}\left( \Delta \text{ACD} \right)$ to both sides, we get

⇒ $\text{ar}\left( \Delta \text{ABC} \right)+\text{ar}\left( \Delta \text{ADE} \right)+\text{ar}\left( \text{ACD} \right)=\text{ar}\left( \Delta \text{APC} \right)+\text{ar}\left( \Delta \text{ADQ} \right)+\text{ar}\left( \text{ACD} \right)$

⇒ $\text{ar}\left( \text{ABCDE} \right)=\text{ar}\left( \text{APQ} \right)$ 

Hence proved.

8. If the medians of a $\Delta \mathbf{ABC}$ intersect at G, 

show that $\text{ar}\left( \text{AGB} \right)=\text{ar}\left( \text{AGC} \right)=\text{ar}\left( \text{BGC} \right)=\dfrac{1}{3}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \Delta \text{ABC} \right)$.

Ans: Given: - Medians AE, BF and CD of 

To show: - $\text{ar}\left( \text{AGB} \right)=\text{ar}\left( \text{AGC} \right)=\text{ar}\left( \text{BGC} \right)=\dfrac{1}{3}\text{ }\!\!~\!\!\text{ }\times \text{ar}\left( \Delta \text{ABC} \right)$.

Construction: Draw $\text{BP}\bot \text{EG}$

Proof: we know that $\text{AG}=\dfrac{2}{3}\text{AE}$ 

(Centroid divides the median in the ratio $2:1$)

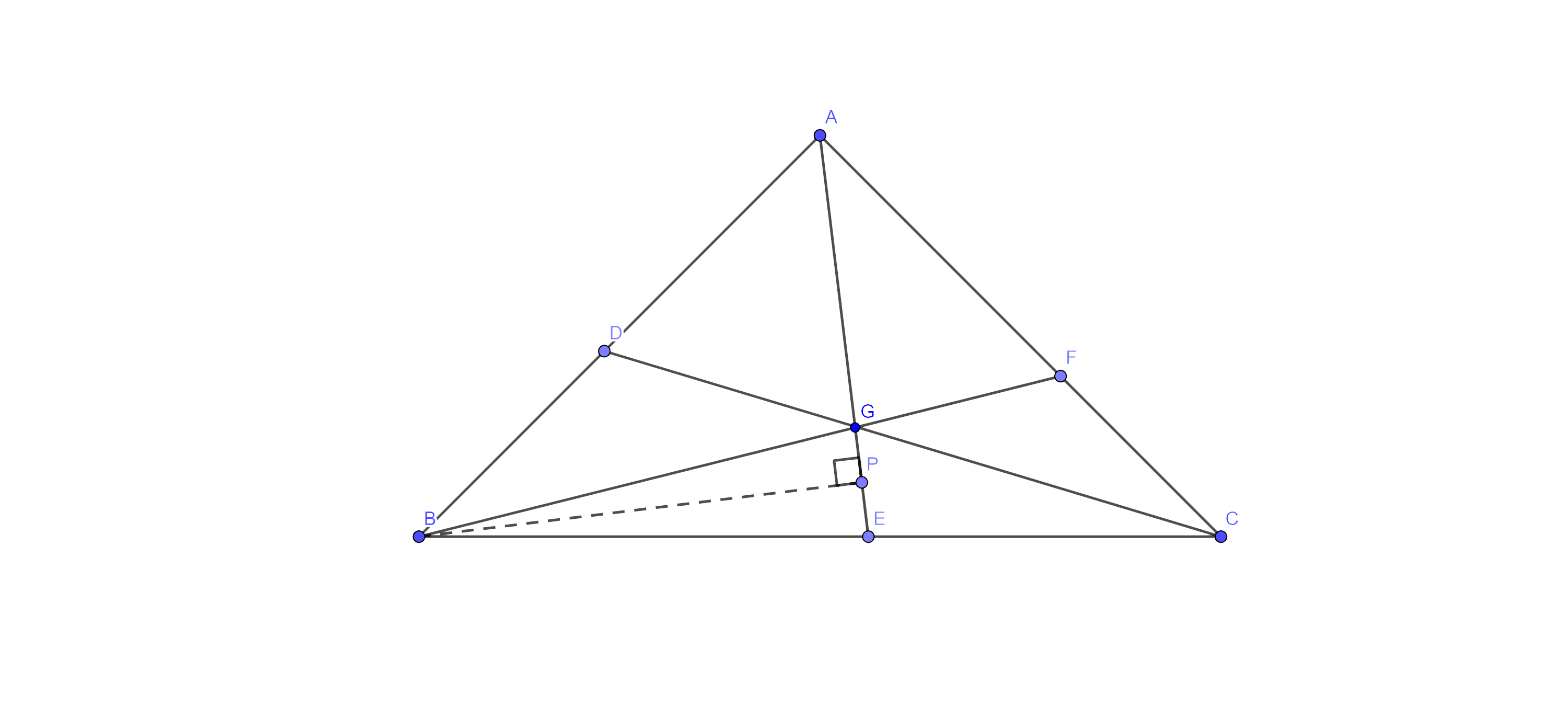
Now, $\text{ar}\left( \Delta \text{AGB} \right)=\dfrac{1}{2}\times \text{AG}\times \text{BP}$

$=\dfrac{1}{2}\times \dfrac{2}{3}\times \text{AE}\times \text{BP}$

$=\dfrac{1}{3}\times \dfrac{1}{2}\times \text{AE}\times \text{BP}$

$=\dfrac{1}{3}\times \text{ar}\left( \Delta \text{ABC} \right)$

Hence proved.

9. In fig. 9.26, X and Y are the mid-points of AC and AB respectively, $\mathbf{QP}\parallel \mathbf{BC}$ and CYQ and BXP are straight lines. 

Prove that $\text{ar}\left( \text{ABP} \right)=\text{ar}\left( \text{ACQ} \right)$.

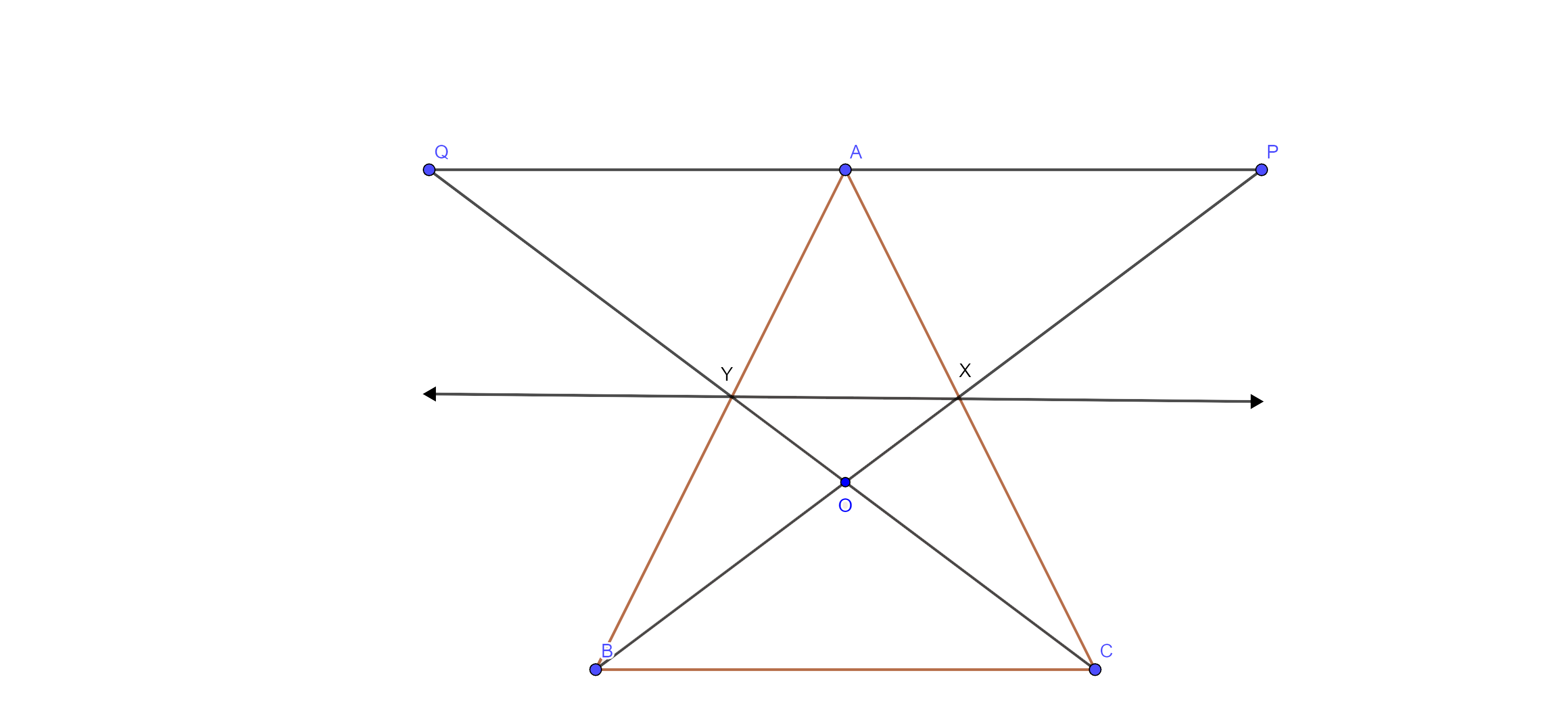
Ans: Given: X and Y are the mid-points of AC and AB respectively, $\text{QP}\parallel \text{BC}$ and CYQ and BXP are straight lines.

To prove: - $\text{ar}\left( \text{ABP} \right)=\text{ar}\left( \text{ACQ} \right)$

Proof: - here, in $\Delta \text{ABC},\text{ }\!\!~\!\!\text{ }$X and Y are the mid-points of AB and AC.

$\therefore \text{XY}\parallel \text{BC}$  (by mid-point theorem)

Since triangles on the same base BC and between the same parallels $\left( \text{XY}\parallel \text{BC} \right)$ are equal in area

⇒ $\text{ar}\left( \Delta \text{BYC} \right)=\text{ar}\left( \Delta \text{BXC} \right)$ ……….. eq(i)

Subtracting $\text{ar}\left( \Delta \text{BOC} \right)$ from both sides, we get

⇒ $\text{ar}\left( \Delta \text{BYC} \right)-\text{ar}\left( \Delta \text{BOC} \right)=\text{ar}\left( \Delta \text{BXC} \right)-\text{ar}\left( \Delta \text{BOC} \right)$

⇒ $\text{ar}\left( \Delta \text{BOY} \right)=\text{ar}\left( \Delta \text{COX} \right)$……… eq (ii)

Adding $\text{ar}\left( \Delta \text{XOY} \right)$ to both sides of eq (ii), we get

⇒ \[\text{ar}\left( \Delta \text{BOY} \right)+\text{ar}\left( \Delta \text{XOY} \right)=\text{ar}\left( \Delta \text{COX} \right)+\text{ar}\left( \Delta \text{XOY} \right)\]

⇒ $\text{ar}\left( \Delta \text{BYX} \right)=\text{ar}\left( \Delta \text{CXY} \right)$ ……… eq (iii)

Now, quad. XYAP and XYQA are on the same base XY and between the same parallels XY and PQ.

⇒ $\text{ar}\left( \text{XYAP} \right)=\text{ar}\left( \Delta \text{XYQA} \right)$ ……… eq (iv)

Adding eq (iii) and (iv)

⇒ $\text{ar}\left( \Delta \text{BYX} \right)+\text{ar}\left( \text{XYAP} \right)=\text{ar}\left( \Delta \text{CXY} \right)+\text{ar}\left( \Delta \text{XYQA} \right)$

⇒ $\text{ar}\left( \Delta \text{ABP} \right)=\text{ar}\left( \Delta \text{ACQ} \right)$

Hence proved.

10. In fig. 9.27, ABCD and AEFD are two parallelograms. Prove that $\mathbf{ar}\left( \mathbf{PEA} \right)=\mathbf{ar}\left( \mathbf{QFD} \right).$

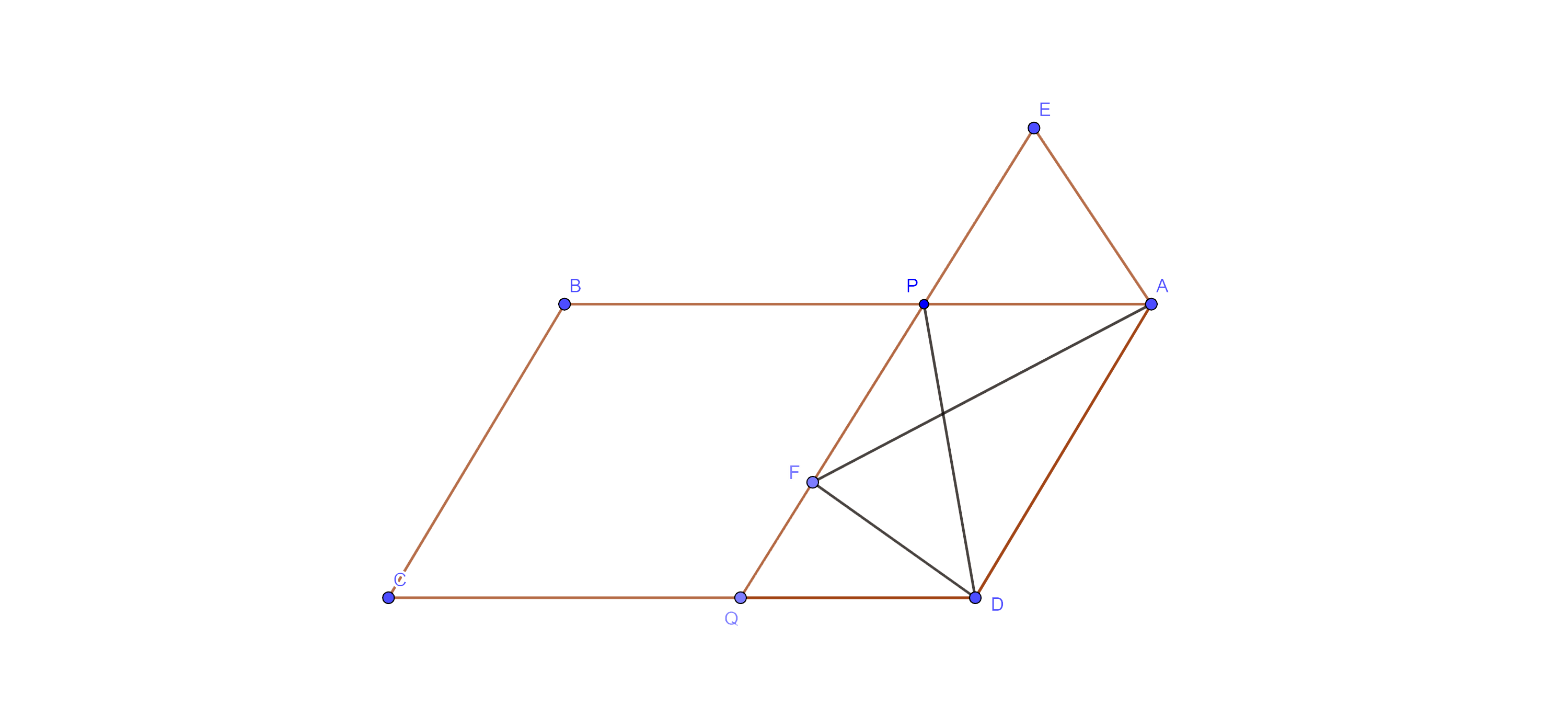
Ans: Given: ABCD and AEFD are two parallelograms

To prove: $\text{ar}\left( \text{PEA} \right)=\text{ar}\left( \text{QFD} \right)$

Proof: - Join PD, here ABCD and AEFD are two parallelograms

Now, in $\Delta \text{PEA}$ and $\Delta \text{QFD}$, we have

⇒ $\angle \text{APE}=\angle \text{DQF}$   (corresponding angles, $\text{AB}\parallel \text{CD}$)

⇒ $\angle \text{AEP}=\angle \text{DFQ}$    (corresponding angles, $\text{AE}\parallel \text{DF}$)

And AE = DF   (opp. sides of a $\parallel \text{gm}$ are equal)

$\therefore \text{ }\!\!~\!\!\text{ }\Delta \text{PEA}\cong \Delta \text{QFD}$  (by AAS cong. Rule)

Therefore, $\text{ar}\left( \Delta \text{PEA} \right)=\text{ar}\left( \Delta \text{QFD} \right)$  

Hence proved.

NCERT Exemplar for Class 9 Maths  Solutions Chapter 9

NCERT Exemplar Class 9 Maths Solutions Chapter 9: Areas of Parallelograms and Triangles will clear all of your questions related to the chapter. NCERT Exemplar Maths is a reference book that is suggested by CBSE. The book gives you in-depth detail about the topic related with triangles as well as parallelograms using verifications and various theorems. Chapter 9 of NCERT Exemplar Class 9 Maths has around 4 sections covering 34 questions. These sample questions cover various topics including finding the area of a rhombus, finding the area of a parallelogram, and finding the perimeter of various figures.

In this chapter, the points covered are as for the CBSE Syllabus (2024-25) by our experts and they are as per the following: 

• Areas of parallelograms, on a similar base and between similar parallels

• Area of triangles on a similar base and between similar parallels

• Median of a triangle separating into two triangles figures

To comprehend the course of measurements, this part is fundamental for you. The interaction with the chapter of NCERT Exemplar will help you in improving your understanding of the subject and leading you to secure good marks.