CBSE Class 9 Maths Chapter 9 Important Questions - FREE PDF Download
CBSE Class 9 Chapter 9 Circles explore the world of tangents, chords, and the properties of circles that make them unique. Understanding theorems like the angle subtended by a chord at a point and solving problems involving cyclic quadrilaterals are crucial skills you'll develop here. The CBSE Class 9 Maths Syllabus is designed to build a strong foundation for higher studies. Learning Circles not only helps you excel in exams but also sets the stage for more advanced concepts in higher classes and beyond. Also practising Class 9 Maths Important Questions ensures you're well-prepared for tricky exam patterns and score full marks in problem-solving. By focusing on these, you'll gain confidence and a clear understanding of complex geometrical concepts.






Access Class 9 Maths Chapter 9: Circles Important Questions
Very Short Answer Type Questions: (1 Marks)
1. An angle in the semicircle is
(a) Right angle
(b)
(c)
(d) None of these
Ans: (a) Right angle
If an angle is inscribed in a semicircle, it will be half the measure of a semicircle (
2. If the angles subtended by two chords of a circle at the centre are equal then the chords are
(a) Not Equal
(b) Equal
(c) Angle Equal
(d) Line Equals
Ans: (b) Equal
3. How many circle passing through three non-collinear points
(a) One
(b) Two
(c) Three
(d) Four
Ans: (a) One
4. The constant distance is called
(a) Diameter
(b) Radius
(c) Centre
(d) Circle
Ans: b) Radius
5. Given
(a)
(b)
(c)
(d) none of these
Ans: (b)
6. A circle is drawn. It divides the plane into
(a)
(b)
(c)
(d) No Parts
Ans: (a)
7. The relation between diameter and radius of a circle is
(a)
(b)
(c)
(d)
Ans: (c)
8. If
(a) diameter
(b) secant
(c) chord
(d) radius
Ans: c) Chord
9. What is a diameter
(a)
(b)
(c)
(d)
Ans: (d)
10. The whole arc of a circle is called
(a) Circumference
(b) Semi-circle
(c) Sector
(d) Segment
Ans: (a) circumference
11. One half of the whole arc of a circle
(a) Semi-circle
(b) Circumference
(c) Segment
(d) Sctor
Ans: (a) semi-circle
12. Circle having same centre are said to be
(a) Concentric
(b) Circle
(c) Chord
(d) Secant
Ans: (a) Concentric
13. The line which meet a circle in two points is called a
(a) Chord of Circle
(b) Diameter
(c) Radius
(d) Secant of Circle
Ans: (d) Secant of Circle
14. The sum of either pair of opposite angle of cyclic quadrilateral is
(a)
(b)
(c)
(d)
Ans: c)
15. Two circle are congruent if they have equal.
(a) Diameter
(b) Radius
(c) Chord
(d) Secant
Ans: (b) Radius
16. The
(a) Semi-Circle
(b) Circumference
(c) Sector
(d) Segments
Ans. (a) Semi-Circle
Short Answer Type Questions : (2 Marks)
1. Fill in the Blanks:
(i) The centre of a circle lies in__________ of the circle.
Ans: Interior
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in_______________ of the circle.
Ans: Exterior
(iii) The longest chord of a circle is a _______________ of the circle.
Ans: Diameter
(iv) An arc is a _______________ when its ends are the ends of a diameter
Ans: Semi-circle
(v) Segment of a circle is the region between an arc and _______________ of the circle.
Ans: Chord
2. Write True or False:
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
Ans: True
(ii) A circle has only finite number of equal chords.
Ans: False
(iii) If a circle is divided into three equal arcs each is a major arc.
Ans: False
(iv) A chord, which is twice as long as its radius is a diameter of the circle.
Ans: True
(v) Sector is the region between the chord and its corresponding arc.
Ans: False
(vi) A circle is a plane figure.
Ans: True
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
Ans: Given:
To prove:
Construction: Draw
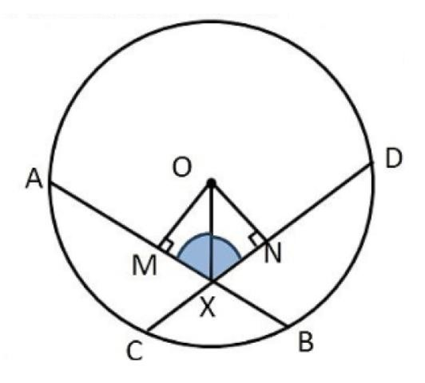
Proof: In right angled triangles
4. In figure,
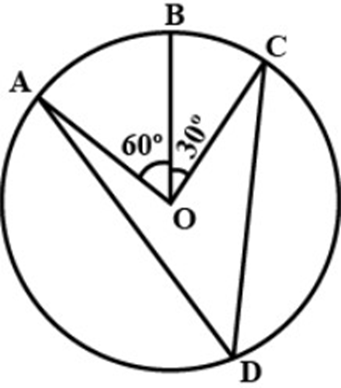
If
Ans:
Now
Angled subtended by an arc, at the centre of the circle is double the angle subtended by the same arc at any point in the remaining part of the circle
5. In figure,
Ans: In the figure,

Now
Now
Now in isosceles triangle OPR,
6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E.

Ans: Here,
And
Now ABCD is a cyclic quadrilateral.
(Sum of opposite angles of a cyclic quadrilateral is supplementary)
7. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Ans. Given: A trapezium
To prove: The points A, B, C, D are concyclic.
Construction: Draw DE .
Proof: Since DE||CB and EB||DC.
Now
But
Hence,
8. Two circles intersect at two points
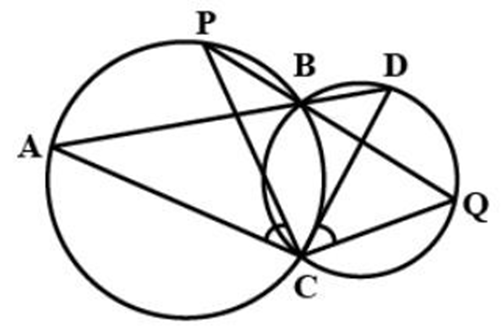
Ans: In triangles
Subtracting
Hence proved.
9. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

Ans: Let two circles with respective centers
We have to prove
Proof: In triangles
10. Prove that the circle drawn with any drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.

Ans: Let
As we know that diagonals of a rhombus bisect and perpendicular to each other.
And if we draw a circle with side
11.
Ans: In
12. Prove that
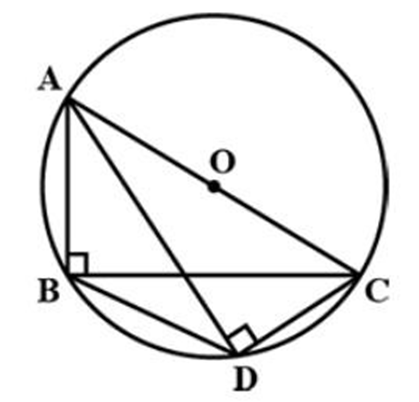
Ans:
Now, chord CD subtends
13. In isosceles triangle
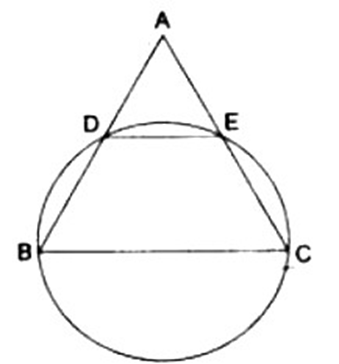
Ans: In triangle ABC, given AB=AC
So
Now ,BCED forms a cyclic quadrilateral
From (i) and (ii) we get
Hence DE || BC
14. Prove that cyclic parallelogram is a rectangle.
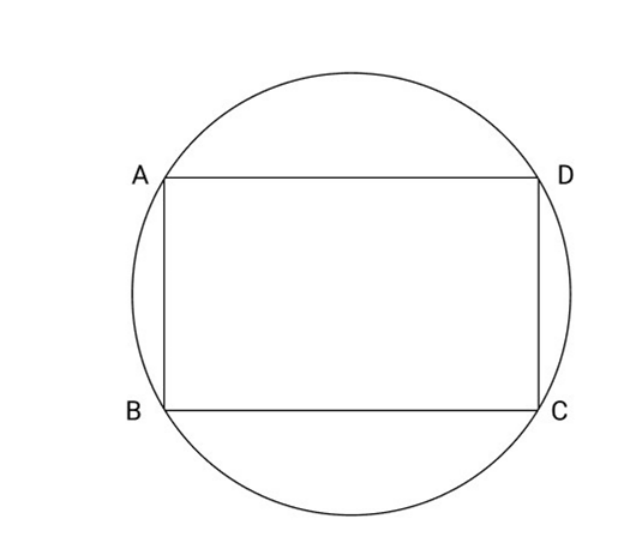
Ans: Let ABCD be the given cyclic parallelogram
(Opposite angle of a parallelogram are equal) ........(ii)
From (i) and (ii)
So, ABCD is a parallelogram having one angle
Hence,
15. A line is Passing through the centre of a circle. If it bisects chord AB and CD of the circle. Prove that

Ans: Line EF passes through the centre
But the line joining the mid-point of a chord to the centre of the circle is perpendicular to the
chord.
Hence,
16.
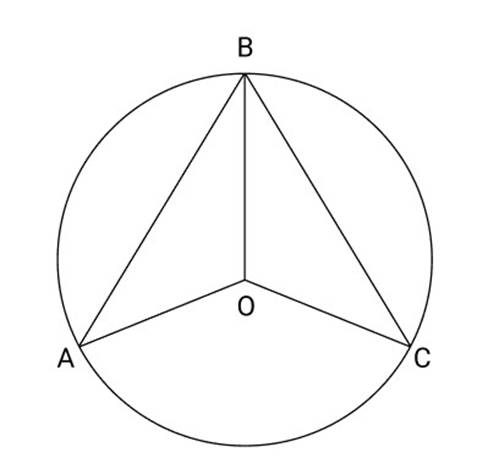
Ans: Join OA and OC
In
Hence, BO bisects
17. If
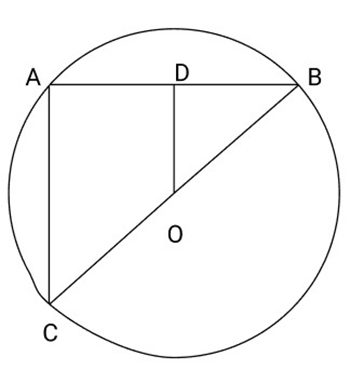
Ans: Join AC Given that
O is the mid-Point of BC
Now in
OD is the line joining the mid points of sides
Hence proved.
18. Given a method to find the centre of a circle
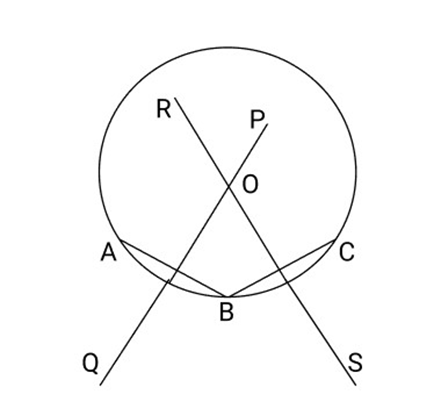
Ans: Take three distinct points (non-collinear)
Now,
19.
Ans:
In
20. Two different circle can't interact each other at more than two points so, prove it.

Ans: Let the two different circles intersect in three points
We know that through three non-collinear Points, one and only one circle can pass so, it contradicts the hypothesis.
21. In the given figure,
Ans: Perpendicular drawn from the centre to the chord bisects the chord.

In right angled triangle BPO,
Hence, the length of chord is equal to 8 cm.
22. If OA is perpendicular to

Ans:
In right angles triangle
23. Prove that ADE is an isosceles triangle if
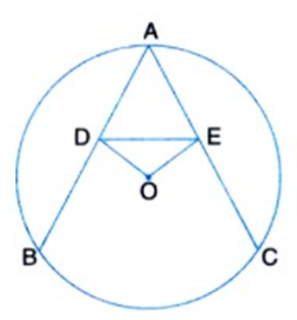
Ans: Given that
Subtracting (i) from (ii)
24. Prove that the exterior angle formed by producing a side of a cyclic quadrilateral is equal to the interior opposite angle.

Ans:
25. Show that

Ans: We know that equal chords of a circle are equidistant from the centre
In
26. From the above question. Show that
Ans:
Adding equal to equals we get
27. Show that
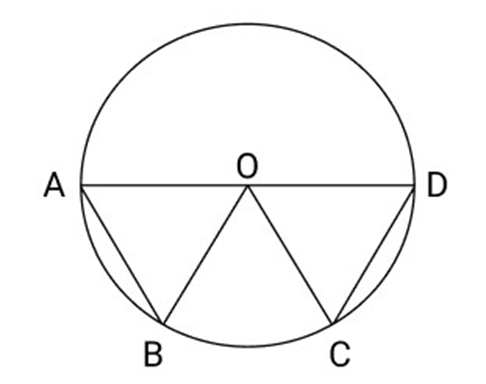
Ans: In
28. Prove that OM Bisect AB. If
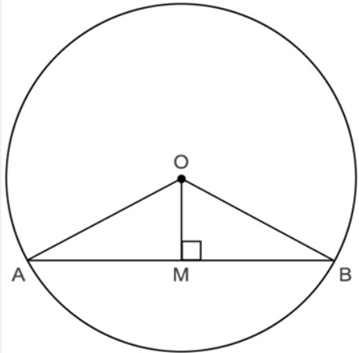
Ans:
Hence OM bisects AB
29. Prove that
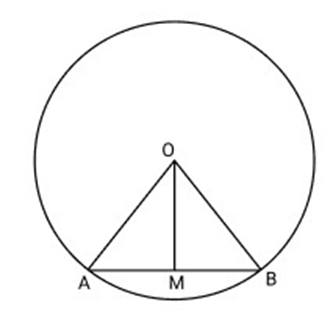
Ans:
But
Thus,
Hence,
30. ABCD is a cyclic quadrilateral in a circle with centre
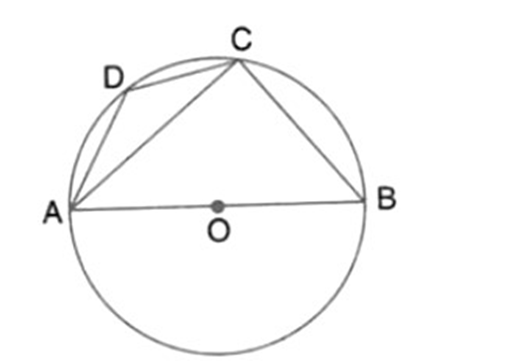
Ans: If we join
Short Answer Type Questions: (3 Marks)
1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.

Ans: I Part: Two circles are said to be congruent if and only if one of them can be superposed on the other so as to cover it exactly
Let
Hence, we can say that two circles are congruent, if and only if they have equal radii.
II Part: Given: In a circle
To Prove:
Proof: In
Hence Proved.
2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal
Ans: Given: In a circle
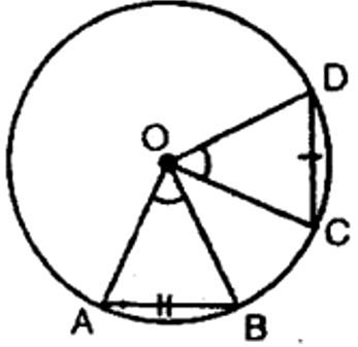
To Prove:
Proof: In
Hence proved.
3. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?

Ans: From the figure, we observe that when different pairs of circles are drawn, each pair have two points (say A and B) in common.
Maximum number of common points are two in number.
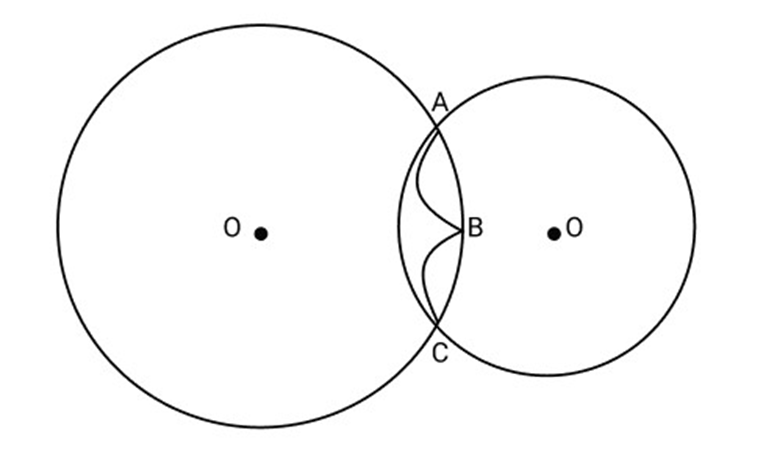
Suppose two circles
Then
We know that:
There is one and only one circle passing through three non-collinear points.
Therefore, a unique circle passes through
A contradiction to the fact that
Hence two different circles cannot intersect each other at more than two points.
4. Suppose you are given a circle. Give a construction to find its centre.
Ans. Steps of construction:
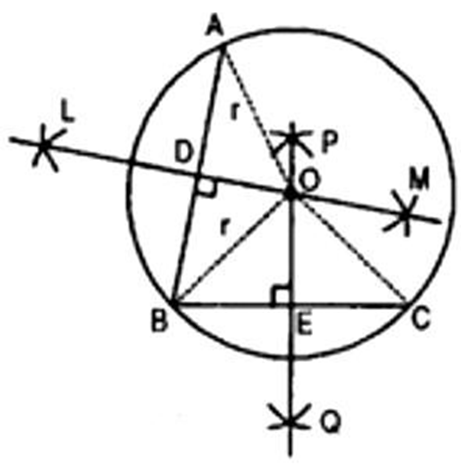
(a) Take any three points
(b) Join
(c) Draw perpendicular bisector say LM of
(d) Draw perpendicular bisector PQ of BC.
(e) Let LM and PQ intersect at the point
Then
Verification:
O lies on the perpendicular bisector of
O lies on the perpendicular bisector of
From eq. (i) and (ii), we observe that
Three non-collinear points A, B and
Hence
5. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

Ans: Given: Let
To prove: OO' is the perpendicular bisector of the chord AB.
Construction: Join OA, OB, O'A, O'B.
Proof: In triangles OAO' and OBO',
Now in
And
Also
Since
Hence
6. Two circles of radii
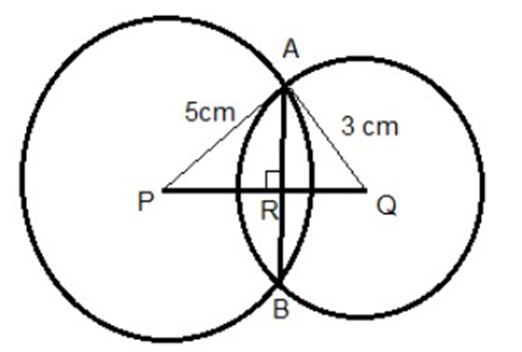
Ans: Let two circles with centres 0 and O' intersect each other at points
Radius
Distance between their centers
In triangle
Hence
Since, perpendicular drawn from the center of the circle bisects the chord.
Hence
Therefore, length of chord
7. If a line intersects two concentric circles (circles with the same centre) with centre 0
at A, B, C and D, prove that
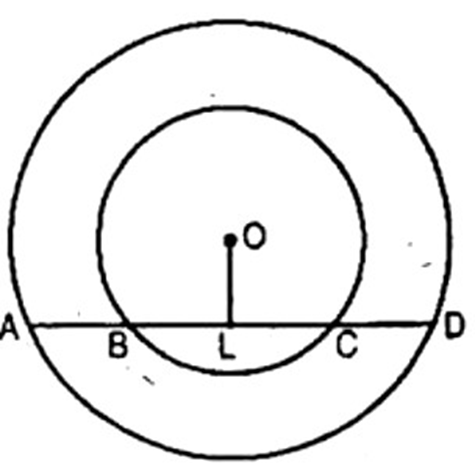
Ans: Given: Line
To prove:
Construction: Draw OL
Proof:
- AL = LD .........(i) [Perpendicular drawn from the centre bisects the chord]
Now,
(ii) (Perpendicular drawn from the centre bisects the chord)
Subtracting (ii) from (i), we get,
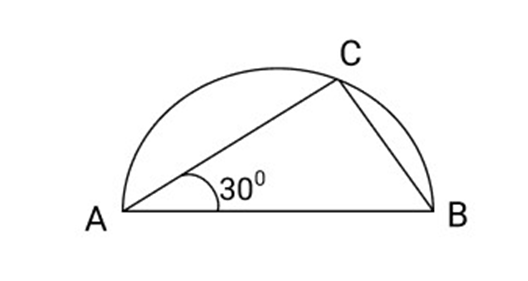
8. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.
Ans: Let

Now
Thus, angle subtended by major arc,
Let
9. In figure,
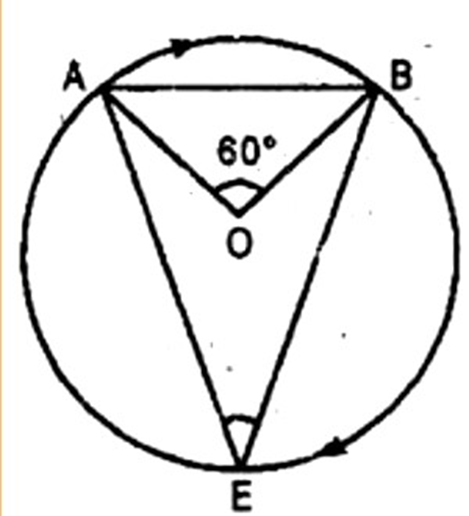
Ans: In triangle
Since,
(Angles subtended by the same arc at any points in the alternate segment of a circle are equal)
10. In figure, A, B, C, D are four points on a circle. AC and BD intersect at a point E such that
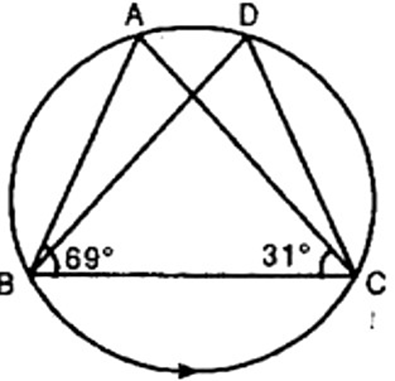
Ans: Given:
Now in
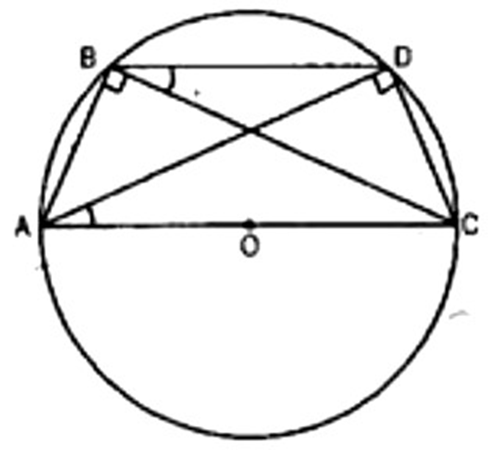
11. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Ans: Since
Similarly,
Now AC = BD (Diameters of same circle)
Similarly,
From eq. (i), (ii), (iii) and (iv), we observe that each angles of the quadrilateral is
Hence
12. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Ans: Given: Two circles intersect each other at points A and B. AP and AQ be their respective diameters.
To prove: Point B lies on the third side PQ.
Construction: Join
Proof: AP is a diameter.
(Angle in semicircle)
Also, AQ is a diameter.
(Angle in semicircle)
Thus point B. i.e. point of intersection of these circles lies on the third side i.e., on PQ.
13.
Ans: We have
If we draw a circle with AC (the common hypotenuse) as diameter, this circle will definitely passes through of an arc AC, Because
Now we have
Hence proved.
14. Two chords
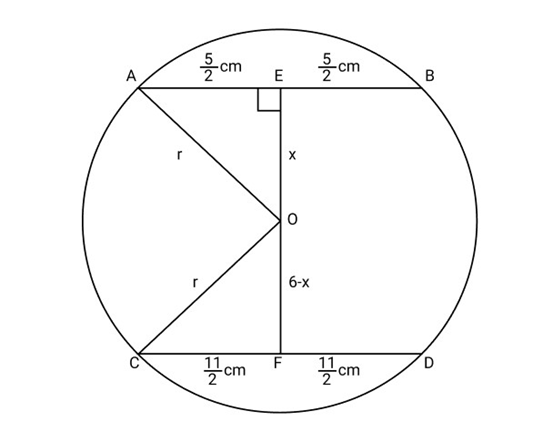
Ans: Let
Join
Since perpendicular from the centre of the circle to the chord bisects the chord.
And
Let
Let radius of the circle be
In right angled triangle AEO,
(Using Pythagoras theorem)
Again, In right angled triangle
(Using Pythagoras theorem)
Equating eq. (i) and (ii),
Now from eq. (i),
Hence radius of the circle is
15. The lengths of two parallel chords of a circle are

Ans: Let
Join
Since perpendicular from the centre of the circle to the chord bisects the chord.
And
Perpendicular distance of chord
Now in right angled triangle AOE,
Perpendicular distance of chord CD from the center
Now in right angled triangle OFC,
Hence distance of other chord from the centre is
16. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced it necessary) at
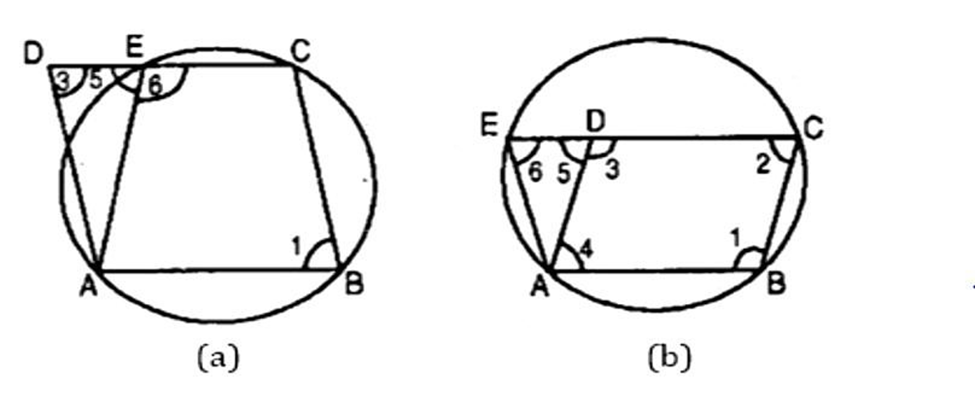
Ans: In figure (a),
ABCD is a parallelogram.
(ii)
And
From eq. (ii) and (iii),
Now, from eq. (i) and (iv),
In figure (b),
Also and
And and EC meets them.
Since
From eq. (i) and (iii),
But from eq. (ii),
Now in triangle AED,
Hence in both the cases,
17. Two congruent circles intersect each other at points
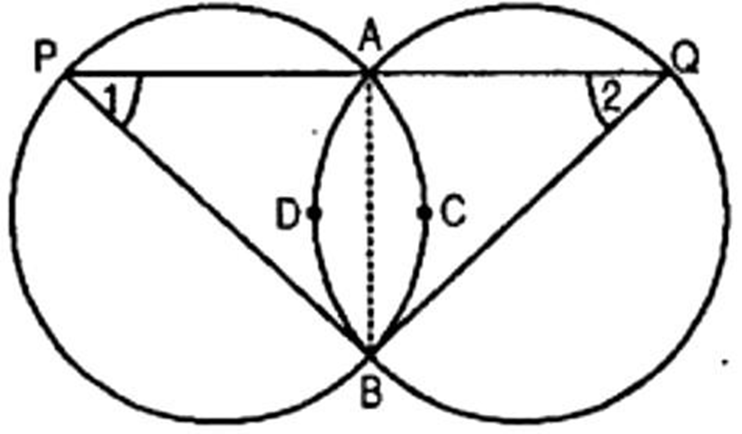
Ans: Given: Two equal circles intersect in
A straight line through A meets the circles in P and Q.
To prove:
Construction: Join
Proof:
Since equal arcs of two equal circles subtend equal angles at any point on the remaining part
of the circle, then we have,
In triangle PBQ,
- Sides opposite to equal angles of a triangle are equal.
Then we have,
18. Pair of opposite sides of a cyclic quadrilateral are equal, Prove that the other two sides are parallel.
Ans: Given: A cyclic quadrilateral
To Prove:
Construction: Join B and D
Proof:
But these are alternate angles
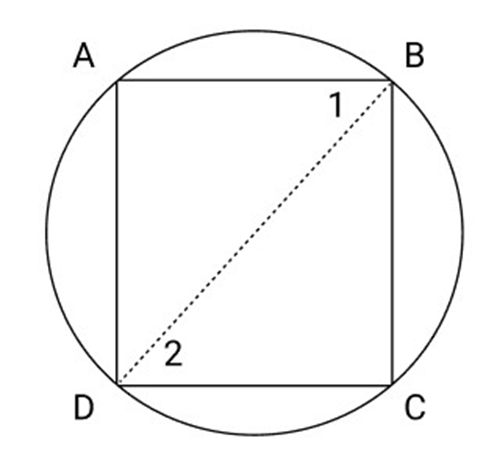
19. Prove that the centre of the circle through A, B, C, D is the Point intersection of its diagonals.

Ans: Given: A cyclic rectangle ABCD in which diagonals AC and BD intersect at Point 0
To Prove:
Proof:
Now as the diagonals
A, B, C, D lie on the same circle.
20. In isosceles triangle ABC, AD = AE and D and
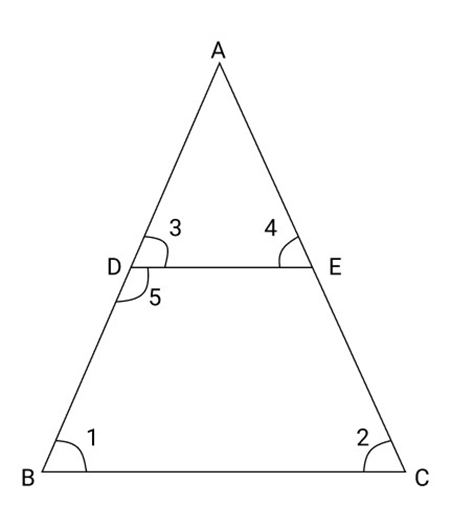
Ans: Given - In
Such that
To prove
Proof
Similarly, In
In
But
Hence
21. If two non - parallel sides of a trapezium are equal, prove that it is cyclic.

Ans: Given:
To prove:
Construction: We draw
Proof: To prove
In
$\begin{array}{ll}
\angle A E D & \left.=\angle B F C \quad \text { (Both } 90^{\circ} \text { as } A E \perp D C \& B F \perp D C\right) \\
A D & =B C \quad \text { (Given) }
\end{array}$
So,
i.e.,
Now, for parallel lines
of transversal are supplementary)
So, in
Hence proved
22. In circle bisector AD of
circle of
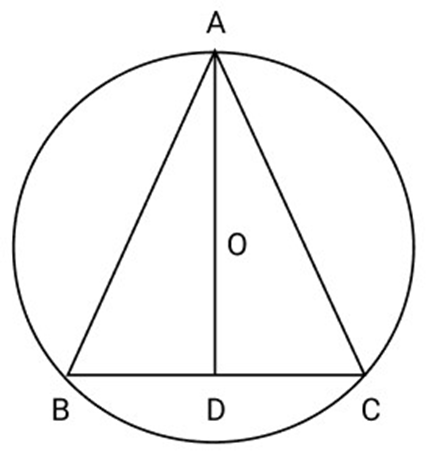
Ans: Draw
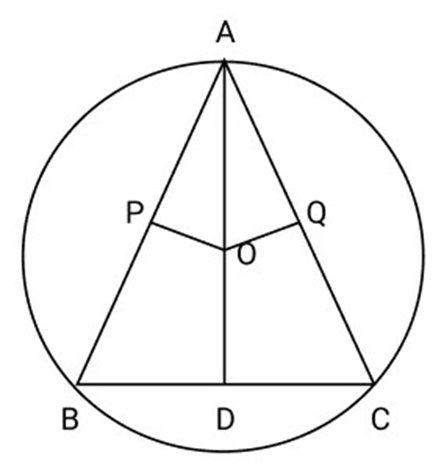
In
Chords
23. Prove that the circle drawn with the equal sides as a diameter passes through the Point D. if

Ans: Given
Which intersects the side
To prove
Construction - Join AD.
Proof
But
Now in right
Side AD = AD [ Common]
The corresponding parts of the congruent triangle are congruent.
Hence
24. If a Pair of opposite sides of a cyclic quadrilateral are equal, then the diagonals are also equal.

Ans: Given: A cyclic quadrilateral
To Prove: diagonal
Proof:
But these are the angles subtended by the diagonals AC and BD in the same circle
25.
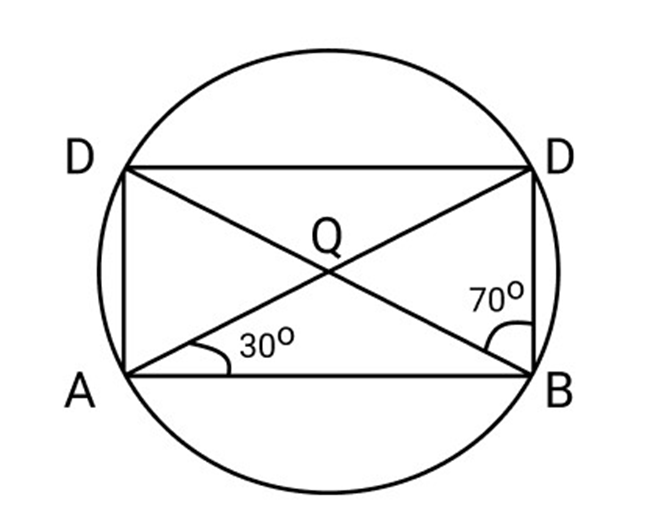
Ans:
26. AB is chord of a circle and AB Produced to
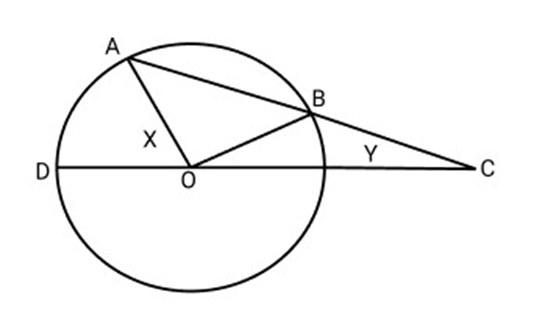
Ans: Proof: In
In
Again in
Hence proved.
27. Prove that
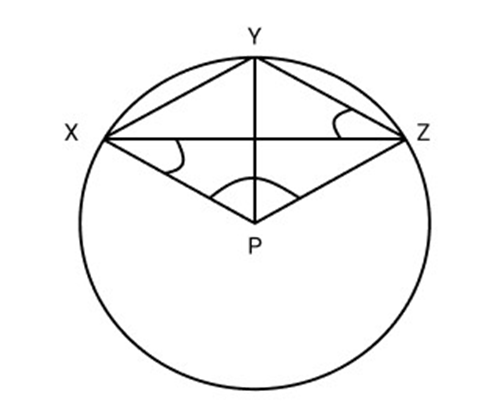
Ans: Given: A circle with centre P, XY and YZ are two chords
To Prove:
Proof:
Similarly arc YZ subtends
Adding (i) and (ii)
28. Prove that OA is the perpendicular bisector of

Ans: Let OA intersect BC in P produce AO to meet the circle at
Now, AOK is the diameter
In
Each
29. Prove that the line joining the midpoint of the two parallel chords of a circle passes through the centre of the circle.

Ans: Let
POQ is a straight line.
30.
Ans: Join
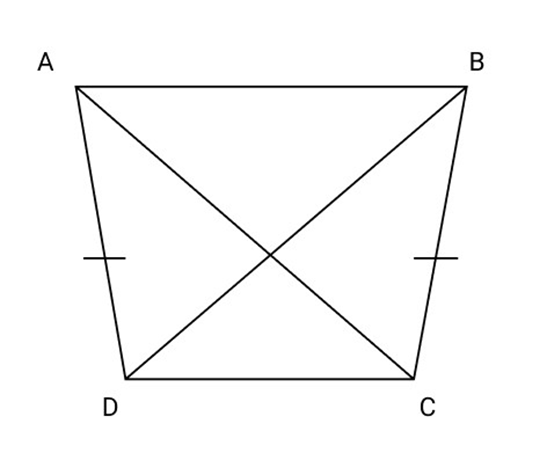
In
As these are two equal angles on the same side of a line segment
The four points
31. Prove that diagonal is also equal when pair of opposite sides of a cyclic quadrilateral are equal.

Ans: Given: A cyclic quadrilateral
To Prove: diagonal AC= Diagonal BD
Proof:
But these are the angle subtended by the diagonal AC and BD in the same circle.
32. In ABCD cyclic quadrilateral diagonal Intersect at
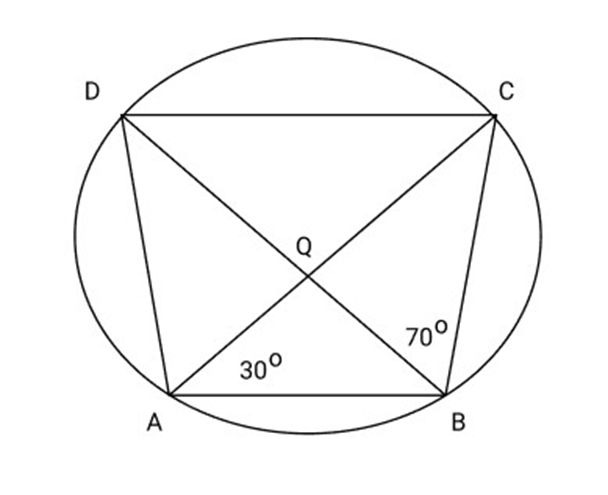
Ans:
33. Find the value of

Ans:
34. Calculate the measure of
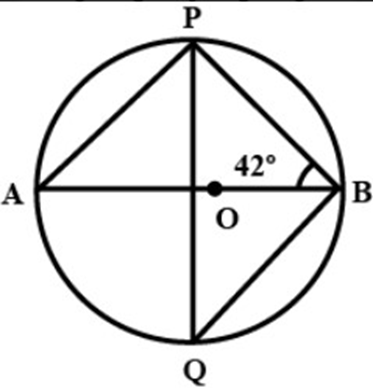
Ans:
35. In the given Fig
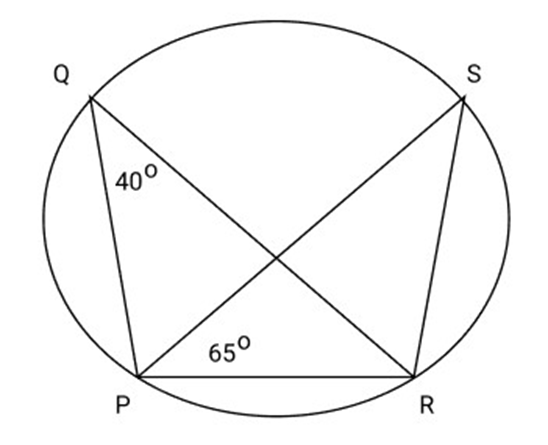
Ans:
36. Find the length of AB, CD,AC and BD if two concentric circles with centre 0 have
A,B,C,D as the Point of intersection with line

Ans:
From (i) and (ii)
Long Answer Type Questions: (4 Marks)
1. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Ans: Given: Let
O intersecting each other at point
To prove: (a)
Construction: Draw
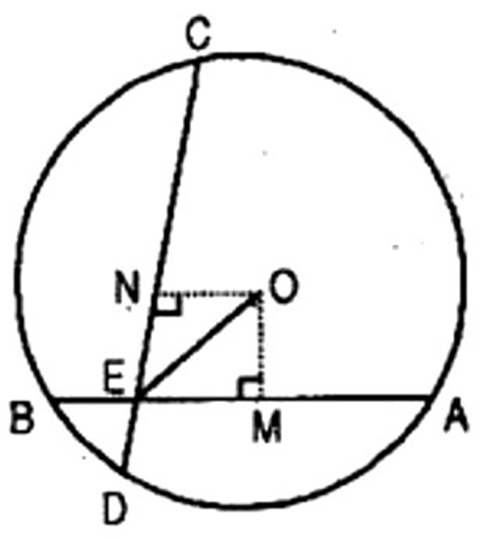
Proof: In right triangles OME and ONE,
(Equal chords are equidistance from the centre)
Now,
Similarly,
But
From eq. (ii) and (iii),
Also
Adding (i) and (iv), we get,
Now
2. Three girls Reshma, Salma and Mandip are standing on a circle of radius

Ans: Let Reshma, Salma and Mandip takes the position C, A and B on the circle.
Since
The centre lies on the bisector of
Let
Again, since
Let
From right angled triangle OMB,
Again, in right angled triangle AMB,
Equating the value of
Hence, from eq. (i),
3. A circular park of radius
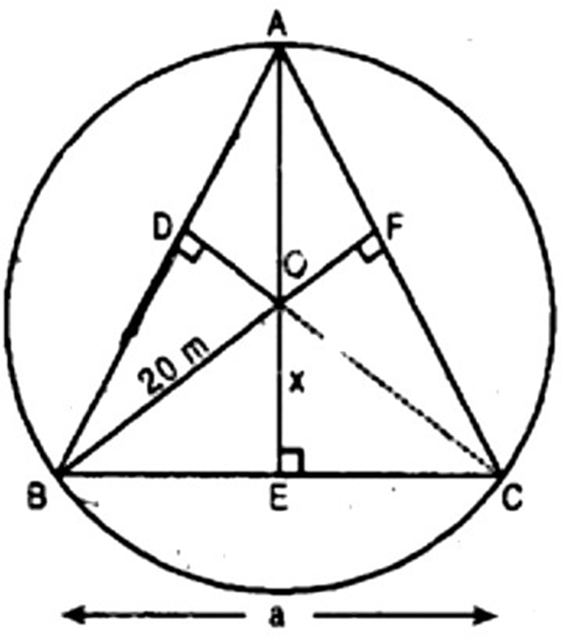
Ans: Let position of three boys Ankur, Syed and David are denoted by the points
respectively.
Since equal sides of equilateral triangle are as equal chords and perpendicular distances of equal chords of a circle are equidistant from the centre.
Join
And
Area of
Now,
Now in right angled triangle BEO,
And
Thus, distance between any two boys is
4. Let vertex of an angle ABC be located outside a circle and let the sides of the angle intersect chords AD and CE with the circle. Prove that

Ans: Vertex B of
Side AB intersects chord CE at point
circle.
We have to prove that
Join
Now
[Angle subtended by an arc at the centre of the circle is twice the angle subtended by the same arc at any point in the alternate segment of the circle]
Similarly
Subtracting eq. (ii) from eq. (i),
Now
Also
Using eq. (iv) and (v) in eq. (iii),
Or
Hence proved.
5. AC and BD are chords of a circle which bisect each other.

Prove that:
(i) AC and BD are diameters.
Ans: Given: AC and BD of a circle bisect each other at
Then
To prove:
(i) AC and BD are the diameters. In other words,
Proof: (i) In triangles AOD and BOC,
Similarly,
circle.
AC is the diameter. [Proved in (i)]
Similarly, BD is the diameter.
(ii) ABCD is a reactangle
Ans: [Angle in semi-circle]
Now diameters
Similarly,
From eq. (i), (ii), (iii) and (iv), we observe that each angle of the quadrilateral is
opposite sides are equal.
Hence
6. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and respectively. Prove that angles of the triangle are

Ans: According to question,
And BE is the bisector of
Also
Since the angles in the same segment of a circle are equal.
And
Adding both equations,
Similarly,
In triangle DEF,
Similarly, we can prove that
7. The bisector of
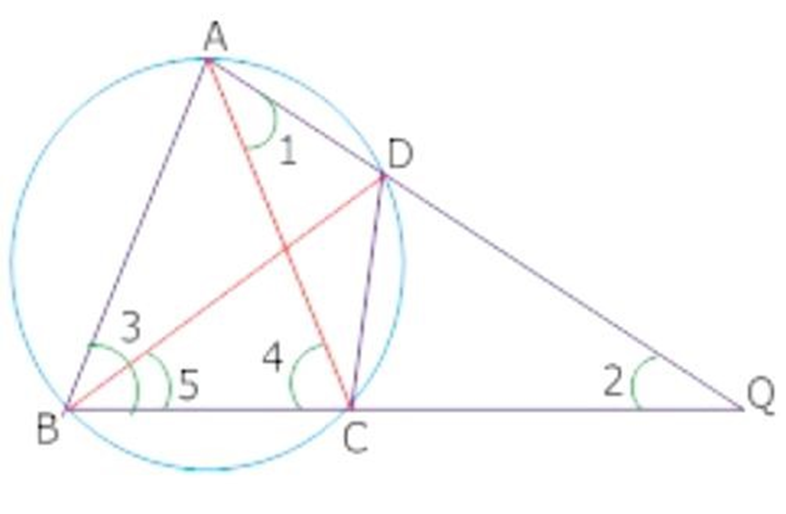
Ans: Join P and C
Considered
(Exterior angle is equal to the sum of two interior opposite angles)
From (i) and (ii)
In
8. OC radius equal to chord
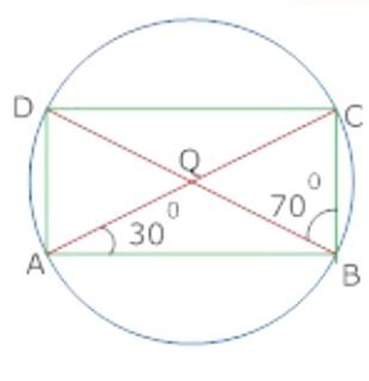
Ans. Join BC
In
Hence,
(Angle subtended by arc
Exterior
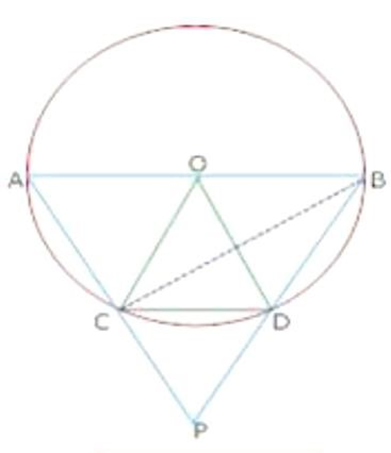
9. The two chords bisect each other AD and BC show that
(i)
Ans: Given that the two chords
Let these cords bisect at
In
Also, in quadrilateral
(ii)
Ans: Since, from the first answer, we can see that we have AC and BD as a diameter and both are equal to each other.
Now we can say that,
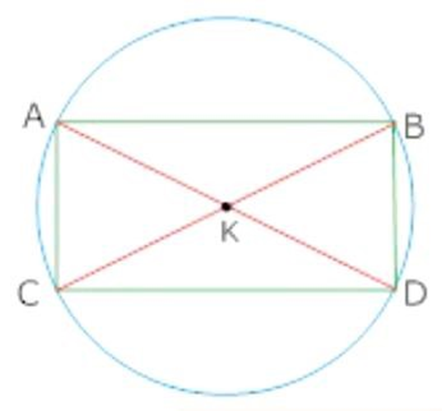
10. Show that
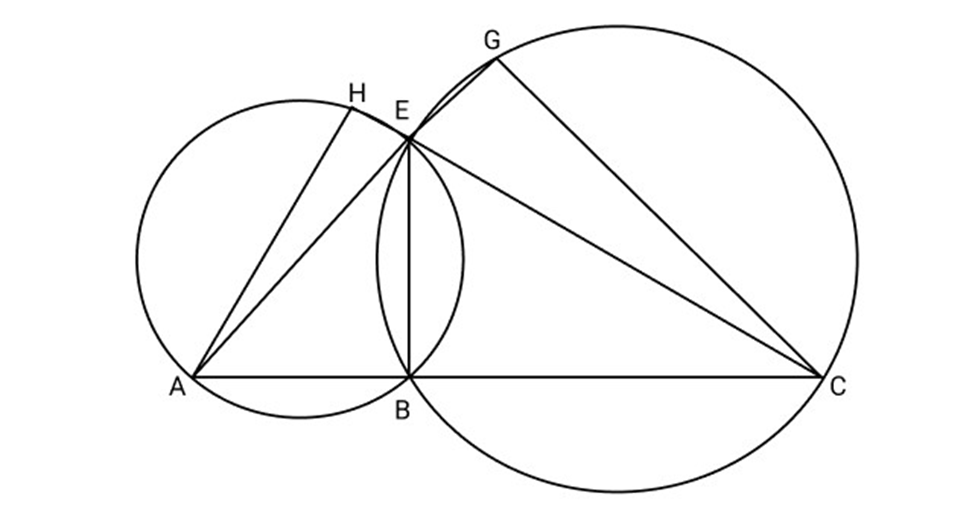
Ans:
Adding (i) and (ii) we get
11. OP
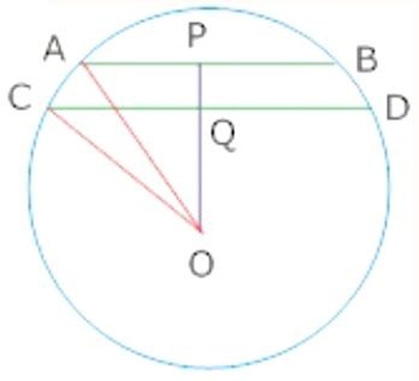
Ans: Join
In right angled triangle
In rt.
Hence, length of PQ= 1 cm
CBSE Class 9 Maths Chapter 9 Important Questions - Free PDF Download
Definition of Circle
A circle is defined as a set of all points in a plane which are equally spaced from a fixed point. The fixed point is called the centre of the circle and the distance between any point on the circle and its centre is called the radius of the circle.
Parts of Circle
Based on the positions and their properties a circle has different parts. The important parts of a circle are explained below in detail.
Arc - It is basically the connected curve of a circle.
Sector - A region bounded by two radii and an arc.
Segment - It is the region bounded by a chord and an arc lying between the chord’s endpoints. Points to remember that segments do not contain the centre.
Centre - Midpoint of a circle is known as the centre.
Chord - It is a line segment that joins two points on the circle. Endpoints of the chord lie on the circle.
Diameter - It is a line segment having both the endpoints on the circle and is the largest chord of the circle.
Radius - It is the line segment connecting the centre of a circle to any point on the circle itself.
Secant - It is a straight line which cuts the circle at two points. It is also known as an extended chord.
Tangent - It is a straight line touching the circle at a single point.
Radius of Circle
A line segment connecting the centre of a circle to any point on the circle itself is known as the radius of the circle. The radius is denoted by R or r.
Diameter of Circle
Diameter is defined as the longest chord of the circle. It is twice the length of radius i.e. d = 2r. The radius of the circle can be derived from the diameter of the circle. Formula for radius of circle is given by r= d/2.
All the important point related to the circle are shown below in the diagram

Properties of Circles
The important basic properties of the circle are as follows:
The outer line of a circle ( which is circumference ) is at equidistant from the centre.
The diameter of the circle divides the circle into two equal parts.
Two circles are said to be congruent to each other if they have equal radii.
Circles which are different in size or have different radii are known as similar circles.
The diameter is the largest chord of the circle and is double the radius.
A tangent to a circle is a line which touches the circle exactly at one point. For every point on the circle, There is a unique tangent for every point on the circle passing through it.

The tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact.

Here, O is the centre and OP⊥XY.
Length of a Tangent
The length of the tangent to the circle is defined as the segment of the tangent from the external point A to the point of tangency (B) with the circle. In the given diagram below, AB is the length of a tangent.

Lengths of Tangents Drawn from an External Point
Two tangents of equal length can be drawn from an external point of a circle.

PT = QT
Area of Circle:
The space occupied by the shape circle is known as an area of the circle. The area of a circle is given by the formula below
Area of Circle, A = πr² Square units
Circumference of Circle
The circumference of a circle is the length of the line around the edges of the circle. Circumference of a circle is calculated by multiplying pi with 2 times radius. Mathematically can be expressed as
C = 2πr
Important Theorem Related to Circle
Equal chord of a circle subtends an equal angle at the centre.
The perpendicular to a chord bisects the chord if the line drawn from the centre of the circle.
Equal chords of a circle are equidistant (i.e equal distance) from the centre of the circle.
The measure of angles subtended to any point on the circumference of the circle from the same arc is equal to half of the angle subtended at the centre by the same arc.
In a cyclic quadrilateral, the opposite angles are supplementary.
5 Important Formulas from Class 9 Maths Chapter 9 Circles
S.No. | Name of the Formula | Formula |
1 | Perpendicular from the centre to a chord bisects the chord | |
2 | Equal chords subtend equal angles at the centre | If AB = CD |
3 | Angle subtended by an arc at the centre and circumference | |
4 | Opposite angles of a cyclic quadrilateral are supplementary | |
5 | Length of tangents drawn from an external point | PA = PB (where P is an external point) |
Tips to learn Class 9 Maths Chapter 9 Circles
Get comfortable with key terms like radius, diameter, chord, arc, tangent, and secant. These are the building blocks for everything else in the chapter.
Draw diagrams for every concept, like tangents, cyclic quadrilaterals, and angles subtended by arcs. Visual learning helps you remember better.
Focus on understanding and applying the main theorems, like “The radius perpendicular to a chord bisects it” and “Equal chords subtend equal angles at the centre.” Practice problems based on these.
Work through important questions related to circles. Start with simpler problems and gradually move to complex ones involving multiple concepts.
Go over your notes and solve examples frequently. Regular revision will help you retain concepts and apply them faster during exams.
Key Takeaways of Important Questions by Vedantu Class 9 Maths Chapter 9 - Circles Free PDF
The circles class 9 questions with solutions allow the students to take several benefits. They are:
Students can score better marks and gain good knowledge.
These PDFs are available for free.
Students can take either a soft copy or hard copy.
Conclusion
CBSE Class 9 Maths Chapter 9 Circles, is a key part that explores geometric concepts. Understanding the properties of tangents, chords, and cyclic quadrilaterals not only builds a strong foundation for higher studies but also sharpens your problem-solving skills. Practising important questions from this chapter helps you focus on critical topics, familiarizes you with common exam patterns, and improves your confidence. By learning these questions, you can ensure better performance in exams and develop a solid understanding of geometry.
Related Study Materials for CBSE Class 9 Maths Chapter 9
S.No | Study Materials for Class 9 Maths Chapter 9 |
1. | |
2. | |
3. | |
4. | |
5. | |
6. |
CBSE Class 9 Maths Chapter-wise Important Questions
S.No | Chapter-wise Important Questions for Class 9 Maths |
1. | |
2. | |
3. | |
4. | |
5. | |
6. | |
7. | |
8. | |
9. | |
10. | |
11. |
Related Important Links for Maths Class 9
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 9–
S.No | Study Materials for Class 9 Maths |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9. |
FAQs on Circles Class 9 Important Questions: CBSE Maths Chapter 9
1. How to score full marks in CBSE Class 9 Maths?
To score full marks in CBSE Class 9 Maths, focus on thoroughly understanding concepts, practising NCERT exercises, and memorizing all formulas and theorems. Regularly solve sample papers, mock tests, and previous years’ questions to improve speed and accuracy. Clear doubts immediately and present solutions step-by-step with proper diagrams in the exam.
2. What is the structure of a circle?
The parts of a circle are the radius, diameter, circumference, arc, chord, secant, tangent, sector and segment.
3. What are the important terms in circles Class 9?
Chord, Secant, Diameter, Arc, Segment, Sector, Tangent.
4. How to understand Circles chapter Class 9?
To understand the Circles chapter in Class 9, start by learning the basic definitions like radius, diameter, chord, and tangent. Focus on key theorems such as the angle subtended by a chord and properties of cyclic quadrilaterals. Practice plenty of NCERT questions and diagrams to visualize concepts clearly. Regular revision and solving sample problems will help build confidence. You can refer to Class 9 Chapter 9 - Circles Solutions Vedantu for in-depth understanding.
5. What is the formula for circle?
The area of a circle is pi times the radius squared (A = π r²).
6. In Class 9 Maths Ch 9 what is the property of a radius perpendicular to a chord in a circle?
The radius perpendicular to a chord always bisects the chord, dividing it into two equal parts. This is a key concept from Class 9 Maths Chapter 9 that often appears in important questions. Understanding this will help in solving problems related to chords.
7. How do you prove that the angle subtended by an arc at the centre is twice the angle subtended on the circumference according to class 9 maths?
The angle subtended at the centre is always twice the angle subtended on the circumference by the same arc. This is a vital theorem in CBSE Class 9 Maths Chapter 9 and is frequently tested in important questions for the exam.
8. What is the relationship between the lengths of tangents drawn from an external point to a circle?
The lengths of the tangents drawn from an external point to a circle are always equal. This property is crucial in solving problems in Class 9 Maths Chapter 9 and often appears in important questions.
9. Why is a cyclic quadrilateral important in the study of circles?
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. The opposite angles of a cyclic quadrilateral add up to 180°, which is an essential theorem for Class 9 Maths Chapter 9 that often features in important questions.
10. How do you solve problems involving the length of a chord in a circle?
To solve problems involving the length of a chord, you often need to apply the Pythagoras theorem and use properties like the radius and perpendicular bisector. This concept is crucial in Class 9 Maths Chapter 9 and commonly appears in important questions.





























