What Are Nodes in Molecular Orbitals Definition Types and Formula Explanation
The wave-like features of electrons are referred to in chemistry as "orbitals," which are quantum mechanical waves. There are nodes and antinodes on a large number of these quantum waves. There have been points along the media that seem to be stationary, which is a common feature of all standing wave patterns. These locations are known as nodes, which are also frequently known to be points of no displacement.
A positive significant displacement and a large negative displacement are experienced at other places along with the media. They represent the node points that experience the greatest displacement throughout every standing wave vibrating cycle. These points are referred to as antinodes since they are in some ways the counterpart of nodes.
An alternate sequence of nodes and antinodes makes up a standing wave pattern in all cases. Whenever a standing wave pattern forms in a media, the nodes and antinodes are continuously found at the similar point throughout the medium and remain stationary. The pattern has been given the term standing wave as a result of this quality. Through this article, let’s discuss more about the meaning of nodes, examples of nodes, and also the anti-nodes.
What is Node in Chemistry?
In Chemistry, the meaning of node is a point where there is a low probability of discovering electron density. The only plane that passes through the nuclei is the nodal plane, and electrons cannot be found on this plane. Atomic orbital or orbital wave functions can indeed be depicted by the combination of 2 wave functions, angular and radial wave functions. A node is a location at which a wave function goes through zero. In Chemistry, there are two types of nodes, they are:
Radial nodes
Angular nodes
Radial nodes are the spherical surfaces surrounding the nucleus where there is no chance of encountering an electron. The term "angular node" refers to the planes or planar regions surrounding the nucleus where there is no chance of discovering an electron.
What is Meant by Node Point?
The node point is the point where the vibration's amplitude is zero.
A standing wave's minimum amplitude is at a node point along the wave's path. The ends of vibrating guitar strings are a good example of a node. The guitarist can alter the effective lengths of the vibrating string as well as consequently the note generated by adjusting the location of the end node using frets.
Standing Wave with Diagram
Relying upon the interference of the 2 waves explains the positions of the nodes and antinodes within a standing wave pattern. Wherever destructive interference happens, the nodes are generated there. Nodes, for example, form when the crest of one wave encounters the trough of a second wave, or when the half-crest of one wave encounters the half-trough of a second wave, etc.
On other side, antinodes are created in regions where constructive interference does take place. For example, a point of significant favourable displacement develops when the crest of 1 wave encounters with the crest of another wave. Since a crest will encounter with a crest after a full cycle of vibration, after which a trough will encounter with a trough after half a cycle, antinodes are constantly bouncing backwards and forwards between these regions of significant positive and huge negative displacement. Since antinodes oscillate between a big positive and huge negative displacement, a standing wave diagram will occasionally show the structure of the medium at two points in time, and one-half vibration cycle separately.
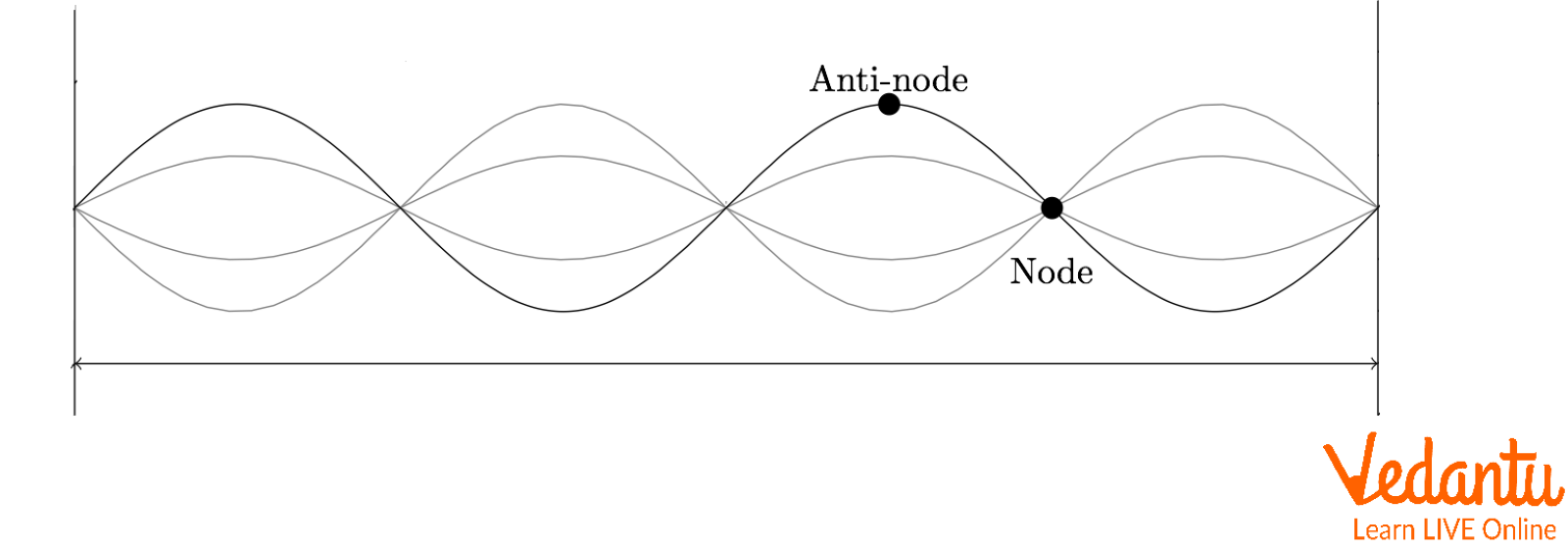
Standing Wave Diagram
Examples of Nodes
Examples of nodes are listed below:
Sand may gather at the nodes of a vibrating Chladni plate to signify points where the plate is stationary.
In the particle in a box model of quantum mechanics, the number of wave function nodes can be used to estimate the quantum energy state; zero nodes correlate to the ground state, 1 node to the first excited state, etc.
Interesting Facts
Several of an atom's or covalent bond's characteristics are determined by the quantity and arrangement of these nodes and antinodes.
2-d standing waves nodes are curves that are frequently circular or straight lines when depicted on basic geometry.
Orbital nodes are locations where the phase of the quantum mechanical wave function Ψ and its square Ψ2 changes. Ψ and Ψ2 are zero at nodes because the phase is likely changing from positive into negative or conversely.
Many places in orbital’s containing positive and negative phases include the 2s, 2p, and 3d orbitals. Nodes divide these regions apart.
Key Features to Remember
Nodes are the areas or gaps surrounding the nucleus where there is no chance of encountering an electron.
A node is the point where a wave function crosses zero. The nodes are divided into two types: angular nodes and radial nodes.
A radial node is a sphere on which there is no chance of locating an electron. Another name for a radial node is indeed a nodal region.
A plane that goes via the nucleus is called an angular node. Another name for an angular node is indeed a nodal plane.
FAQs on Discussion of Nodes in Molecular Orbital Theory
1. What are nodes in atomic orbitals?
Nodes in atomic orbitals are regions of zero probability where the chance of finding an electron is zero. In quantum chemistry, a node occurs where the wave function (ψ) changes sign, making ψ = 0 at that point. Nodes arise from the mathematical solution of the Schrödinger equation and help define the shape and structure of atomic orbitals such as s, p, d, and f orbitals.
2. How many nodes are present in an orbital?
The total number of nodes in an orbital is given by the formula n − 1, where n is the principal quantum number. This means:
- Total nodes = n − 1
- They include both radial and angular nodes
- Example: For n = 3, total nodes = 3 − 1 = 2 nodes
This rule applies to all atomic orbitals in quantum mechanics.
3. What is the difference between radial nodes and angular nodes?
Radial nodes are spherical regions where electron probability is zero, while angular nodes are planar or conical regions determined by orbital shape. The key differences are:
- Radial nodes: Depend on n and l; calculated as n − l − 1
- Angular nodes: Equal to the azimuthal quantum number l
- Radial nodes affect orbital size; angular nodes affect orbital shape
Both types together make up the total number of nodes in an atomic orbital.
4. What is the formula for calculating radial nodes?
The number of radial nodes is calculated using the formula n − l − 1, where n is the principal quantum number and l is the azimuthal quantum number. For example:
- For a 3s orbital: n = 3, l = 0 → radial nodes = 3 − 0 − 1 = 2
- For a 3p orbital: n = 3, l = 1 → radial nodes = 3 − 1 − 1 = 1
Radial nodes increase as the principal quantum number increases.
5. How do you calculate angular nodes in an orbital?
The number of angular nodes in an orbital is equal to the azimuthal quantum number (l). This means:
- s orbital (l = 0) → 0 angular nodes
- p orbital (l = 1) → 1 angular node
- d orbital (l = 2) → 2 angular nodes
- f orbital (l = 3) → 3 angular nodes
Angular nodes determine the orientation and shape of atomic orbitals.
6. Why do s orbitals have no angular nodes?
s orbitals have no angular nodes because their azimuthal quantum number is l = 0. Since angular nodes equal l, an s orbital has 0 angular nodes. As a result:
- s orbitals are spherically symmetrical
- Electron density is distributed evenly around the nucleus
- Any nodes present in higher s orbitals (like 2s or 3s) are radial, not angular
7. What is the total number of nodes in a 3p orbital?
A 3p orbital has a total of 2 nodes. This is calculated using n − 1:
- n = 3 → total nodes = 3 − 1 = 2
- Angular nodes = l = 1
- Radial nodes = 3 − 1 − 1 = 1
Thus, a 3p orbital has 1 angular node and 1 radial node.
8. Do nodes affect the energy of an orbital?
Yes, the number of nodes is directly related to the energy of an orbital. As the principal quantum number (n) increases, the number of nodes increases, and the orbital energy generally increases. More nodes mean:
- Greater electron energy
- More complex wave function
- Larger average distance from the nucleus
Thus, higher-energy orbitals have more nodes.
9. What is the significance of nodes in quantum mechanics?
Nodes are significant because they reflect the wave nature of electrons in quantum mechanics. They indicate:
- Points where the wave function ψ = 0
- Changes in the phase (sign) of the wave function
- The quantized energy levels of electrons
Nodes arise naturally from solving the Schrödinger wave equation for hydrogen-like atoms.
10. How are nodes related to quantum numbers?
Nodes are directly determined by the quantum numbers n and l. The relationships are:
- Total nodes = n − 1
- Angular nodes = l
- Radial nodes = n − l − 1
Thus, the principal quantum number (n) controls the total number of nodes, while the azimuthal quantum number (l) determines the number of angular nodes and the shape of the orbital.
