




How Does a Cyclotron Accelerate Particles?
A cyclotron is a device used to accelerate charged particles such as protons, deuterons, and alpha particles to high energies. It operates on the principle of using both electric and magnetic fields to increase the kinetic energy of these particles, making it essential for nuclear and atomic physics experiments.
Definition and Principle of Cyclotron
A cyclotron is a type of particle accelerator that uses a combination of perpendicular electric and magnetic fields to accelerate charged particles in a spiral path. The fundamental principle is that a charged particle moving perpendicular to a uniform magnetic field experiences a Lorentz force, causing it to move in a circular orbit. Each time the particle crosses the gap between the electrodes, an alternating potential difference accelerates it, resulting in increased kinetic energy.
Construction of a Cyclotron
The main parts of a cyclotron include two hollow, semicircular electrodes called “dees” placed inside an evacuated chamber. The dees are separated by a small gap and connected to a high-frequency oscillator. This entire assembly is positioned between the poles of a strong electromagnet, which generates a uniform magnetic field perpendicular to the plane of the dees. Ions to be accelerated are introduced at the center of the chamber.

Working of the Cyclotron
When a positive ion is emitted at the center, the electric field between the dees accelerates it across the gap. As the particle enters a dee, it is shielded from the electric field but experiences a magnetic field, causing it to move in a semicircular path at constant speed. When the particle emerges from the dee, the electric field reverses direction due to the oscillator, accelerating it once more.
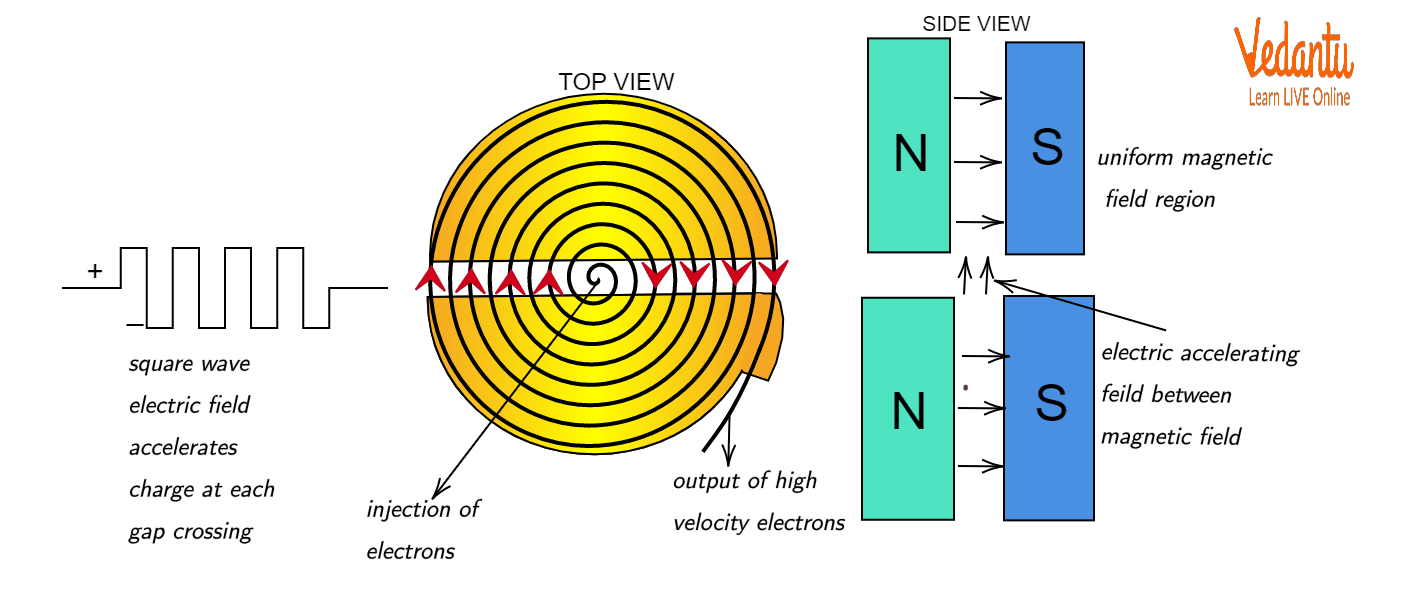
Each time the particle traverses the gap, its speed increases, and it moves in a spiral path of increasing radius. The process repeats until the particle reaches the rim of the cyclotron, where it is extracted through a deflector for use in nuclear experiments.
The required centripetal force for circular motion is provided by the magnetic Lorentz force. Mathematically, $qvB = \dfrac{mv^2}{r}$ leads to $r = \dfrac{mv}{qB}$. The time taken by the particle to complete one revolution is independent of its speed in the non-relativistic case, given by $T = \dfrac{2\pi m}{qB}$.
The resonance condition requires that the frequency of the applied alternating voltage equals the cyclotron frequency, expressed by $f = \dfrac{qB}{2\pi m}$. This ensures continuous acceleration during each crossing of the gap.
For deeper understanding of related concepts, reference can be made to concepts such as Magnetic Effects of Current and Magnetism.
Key Formulas in Cyclotron Operation
The operation of a cyclotron involves several key mathematical relationships:
- Centripetal force: $F_C = \dfrac{mv^2}{r}$
- Lorentz force: $F_B = qvB$
- Radius of path: $r = \dfrac{mv}{qB}$
- Time for one revolution: $T = \dfrac{2\pi m}{qB}$
- Cyclotron frequency: $f = \dfrac{qB}{2\pi m}$
- Kinetic energy after $n$ revolutions: $K.E. = qVn$ (where $V$ is the voltage across the dees)
Applications of Cyclotron
Cyclotrons are widely utilized in several fields of study and industry owing to their efficient acceleration capabilities and compact design.
- Accelerating charged particles for nuclear reactions
- Producing medical isotopes for diagnostics and treatment
- Radiation therapy for cancer treatment
- Studying nuclear structure and transmutation
- Insertion of ions into solid materials
For interaction with current and electromagnetic topics, see Current Electricity.
Limitations of Cyclotron
Despite its usefulness, the cyclotron has some notable limitations, especially regarding the type of particles it can accelerate and the achievable energies.
- Cyclotrons cannot accelerate neutral particles like neutrons
- Relativistic mass variation limits acceleration of light particles such as electrons
- Efficiency reduces for particles nearing the speed of light
As particle velocity approaches the speed of light, relativistic effects cause mass to increase according to $m = \dfrac{m_0}{\sqrt{1 - v^2/c^2}}$. This results in loss of resonance between the oscillator and particle motion, impairing further acceleration.
For more information on how magnetic fields are generated and interact with currents, refer to Magnetic Field on the Axis of a Current Loop.
Comparison: Cyclotron vs. Linear Accelerator
| Cyclotron | Linear Accelerator |
|---|---|
| Compact and space-efficient | Requires significant length |
| Acceleration in spiral path | Straight-line acceleration |
| Suitable for heavier ions | Can accelerate electrons and lighter ions |
Related Concepts in Magnetism and Cyclotron Motion
The functioning of a cyclotron is based on fundamental magnetic interactions and the properties of charged particles in fields. Related concepts such as Electromagnetic Induction and Alternating Current and Magnetic Field Due to Straight Wire are essential for a comprehensive understanding.
The study of cyclotron motion also introduces the concept of cyclotron frequency, which is the angular frequency at which a charged particle orbits in a magnetic field. The formula is $f_c = \dfrac{qB}{2\pi m}$. Cyclotron radiation refers to electromagnetic radiation emitted when particles spiral in magnetic fields, important in advanced physics applications.
For further details on magnetic field configurations in particle accelerators, refer to topics like Magnetic Field Due to Toroid.
FAQs on What Is a Cyclotron? Definition, Working Principle & Applications
1. What is a cyclotron?
Cyclotron is a type of particle accelerator used to increase the energy of charged particles. It works by making particles spiral outward under the effect of a perpendicular magnetic field and an alternating electric field.
Key points:
- Invented by Ernest O. Lawrence in 1930
- Accelerates charged particles like protons, deuterons, and alpha particles
- Used in nuclear physics and medical applications
2. How does a cyclotron work?
Cyclotron works by accelerating charged particles using a strong magnetic field and a rapidly alternating electric field.
Main steps:
- Particles are injected at the center of two hollow semicircular electrodes called dees
- Magnetic field makes particles move in a circular path
- Alternating electric field accelerates the particles each time they cross the gap between the dees
- Particles gain energy and move in an outward spiral until they are extracted
3. What are the main uses of a cyclotron?
Cyclotrons are used in science, medicine, and industry for accelerating particles.
- Producing radioisotopes for medical diagnosis and treatment
- Conducting nuclear physics experiments
- Producing neutron or proton beams for cancer therapy (proton therapy)
- Material research and analysis
4. Who invented the cyclotron and when?
The cyclotron was invented by Ernest O. Lawrence in 1930. He developed the device to accelerate protons for nuclear experiments, earning the Nobel Prize in Physics in 1939.
5. What is the principle of a cyclotron?
Principle of cyclotron: A cyclotron accelerates charged particles using a perpendicular magnetic field and an alternating electric field.
- Particles move in a circular path inside two D-shaped dees due to the magnetic field
- They are accelerated each time they cross the gap between dees by the electric field
- As speed increases, the particles' path spirals outward
6. What are the main parts of a cyclotron?
Cyclotron consists of several essential components:
- Dees: Two hollow semicircular electrodes placed in a magnetic field
- Magnet: Provides a perpendicular magnetic field
- Oscillator: Supplies alternating high-voltage electric field
- Ion Source: Injects charged particles
- Vacuum Chamber: Maintains very low pressure to avoid collisions
7. What are the limitations of the cyclotron?
Cyclotrons have limitations mainly due to the mass and charge of particles and the relativistic effect.
- Cannot accelerate neutral particles or electrons effectively
- As particle velocity increases to a significant fraction of the speed of light, mass increases (relativistic effect), losing synchronisation with oscillating field
- Maximum energy is limited by the size of the device and magnetic field strength
8. Which particles can be accelerated by a cyclotron?
Cyclotrons can accelerate charged particles such as protons, deuterons, alpha particles, and other ions. They cannot effectively accelerate neutral particles or electrons due to their charge and mass properties.
9. What are the advantages of a cyclotron?
The cyclotron offers several advantages for scientific and medical uses:
- Compact and relatively inexpensive compared to linear accelerators
- Continuous beam production
- Useful for producing medical isotopes
- Easy to operate and maintain
- Can achieve high energies for light charged particles
10. Why can't a cyclotron accelerate electrons effectively?
A cyclotron cannot accelerate electrons efficiently because electrons reach relativistic speeds even at low energies.
- Relativistic mass increase causes loss of synchronisation with oscillating field
- This disrupts acceleration, making cyclotrons ineffective for electrons

































