




How Do You Calculate the Outcome of an Oblique Collision?
Oblique collisions refer to interactions where the line of relative motion between two colliding bodies is not parallel to the line of impact. This type of collision requires analysis of motion in two dimensions and the application of the laws of conservation of momentum and kinetic energy. Oblique collisions are an important part of the physics syllabus for competitive exams such as JEE.
Collision: Definition and Conservation Laws
A collision is an event during which two or more bodies exert very strong forces on each other for a short period, leading to changes in momentum and energy of the bodies involved. Momentum is always conserved during a collision, irrespective of the type of collision.
Physical contact between bodies is not a necessary condition for a collision; even interactions such as those between subatomic particles or astronomical bodies at large distances are classified as collisions based on the change in momentum and energy.
For a focused discussion on linear and angular momentum principles, refer to The Concept of Momentum and Angular Momentum of Rotating Bodies.
Types of Collision: Elasticity and Energy Considerations
Collisions are classified based on energy conservation into elastic, inelastic, and perfectly inelastic collisions. In all these cases, the total momentum of the system is conserved during the interaction.
In an elastic collision, kinetic energy and momentum are both conserved. In an inelastic collision, only momentum is conserved; kinetic energy is partially lost. A perfectly inelastic collision involves maximum loss of kinetic energy, and the bodies stick together after the collision.
A detailed comparative study of different types of collisions is available at Elastic vs Inelastic Collision.
Coefficient of Restitution: Mathematical Representation
The coefficient of restitution, denoted as $e$, quantifies the elasticity of a collision. It is the ratio of the relative speed after collision to the relative speed before collision, measured along the line of impact. The value of $e$ is between 0 and 1, and it is a dimensionless quantity.
The coefficient of restitution is defined as:
$e = \dfrac{\text{Relative speed after collision}}{\text{Relative speed before collision}}$
Values of $e$ for different collisions are presented below:
| Type of Collision | Coefficient of Restitution ($e$) |
|---|---|
| Perfectly Elastic | 1 |
| Inelastic | 0 < e < 1 |
| Perfectly Inelastic | 0 |
Line of Impact and Its Role in Collisions
The line of impact is defined as the common normal at the point of contact between two colliding bodies. It determines the direction along which the main impulse acts during the collision process.
If the centers of mass of both bodies lie on the line of impact, the collision is called central. Otherwise, it is referred to as an eccentric collision.
Oblique Collisions: Concept and Features
An oblique collision occurs when at least one of the colliding bodies approaches the other at an angle to the line of impact. The velocity vectors of the bodies are not parallel to the line joining the centers at the instant of collision.
Oblique collisions are generally analyzed in two dimensions. The velocities of the bodies after collision are resolved along and perpendicular to the line of impact.
For a comprehensive understanding of the mechanics of collision, refer to Understanding Collisions in Physics.
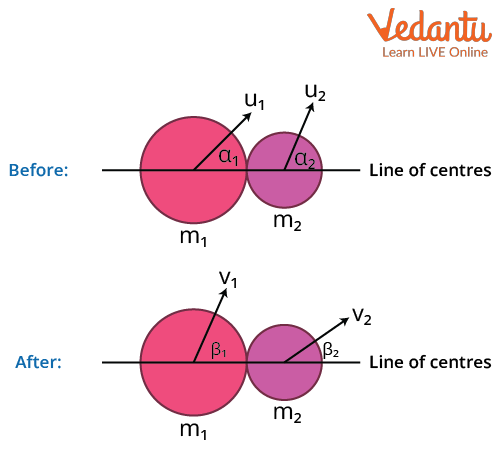
Analysis of Two-Dimensional Oblique Collisions
In two-dimensional oblique collisions, the velocities are split into components parallel and perpendicular to the line of impact. The parallel components are affected during the collision, while the perpendicular components remain unchanged if the surfaces are smooth and there is no external torque.
The conservation of momentum along the line of impact for two bodies ($m_1$, $m_2$) is written as:
$m_1 v_1 \cos\beta_1 + m_2 v_2 \cos\beta_2 = m_1 u_1 \cos\alpha_1 + m_2 u_2 \cos\alpha_2$
Perpendicular to the line of impact, the velocities remain unchanged:
$v_1 \sin\beta_1 = u_1 \sin\alpha_1$
$v_2 \sin\beta_2 = u_2 \sin\alpha_2$
The coefficient of restitution equation for the parallel direction is:
$e = \dfrac{v_2 \cos\beta_2 - v_1 \cos\beta_1}{u_1 \cos\alpha_1 - u_2 \cos\alpha_2}$
These equations allow the determination of final velocities after an oblique collision in two dimensions.
Further details on one-dimensional elastic collisions are available at Elastic Collisions Explained.
Important Points and Formulae for JEE
- Total momentum is always conserved in all types of collisions
- The coefficient of restitution only affects motion along the line of impact
- Perpendicular components remain unchanged in smooth, non-rotational collisions
- The kinetic energy conservation depends on the nature of the collision
- Oblique collisions are analyzed using vector decomposition
Applications and Practice in Oblique Collisions
Oblique collisions are essential in advanced exam problems, including two-dimensional particle collisions and applications in mechanics and modern physics. These principles help solve exam questions that require decomposition of velocities and the use of conservation laws.
Solving practice questions on oblique collisions often requires an understanding of both momentum and energy concepts. For more resources on linear momentum and its applications, see Understanding Linear Momentum.
Summary of Oblique Collisions
Oblique collisions are characterized by non-parallel approach velocities with respect to the line of impact. The primary laws applied are conservation of momentum and, where applicable, conservation of kinetic energy. The coefficient of restitution provides a quantitative measure for the elasticity of the collision.
Accurate vector analysis and conservation equations are necessary to solve oblique collision problems, which are fundamental to understanding collision mechanisms in physics and vital for examinations such as JEE.
FAQs on Understanding Oblique Collisions in Physics
1. What is an oblique collision?
Oblique collision is a type of collision where two bodies collide with their velocities inclined at an angle other than 90° or 0° to the line joining their centers.
- Involves non-head-on contact between objects
- Both tangential and normal velocity components are affected
- Common examples: carom, billiards, ball sports
This concept is crucial in physics for understanding real-world impacts and solving momentum and energy problems per the syllabus.
2. What is the difference between an oblique collision and a head-on collision?
Oblique collisions occur when colliding bodies approach each other at an angle, while head-on collisions happen along the same straight line.
- Oblique collision: Velocities make an angle with the line of impact
- Head-on collision: Velocities aligned with the line joining centers
- Both conserve momentum and energy (depending on elasticity)
Understanding this distinction is essential for solved numerical questions and CBSE exams.
3. What is conserved during an oblique collision?
In an oblique collision, the total momentum of the system is always conserved.
Depending on the type of collision:
- Elastic collision: Both momentum and kinetic energy are conserved
- Inelastic collision: Only momentum is conserved
These conservation laws apply to both the normal and tangential components of motion.
4. How do you resolve velocities in an oblique collision?
To solve oblique collision problems, velocities are resolved into components:
- Split each velocity into normal (perpendicular) and tangential (parallel) to the line of impact
- Apply conservation of momentum and coefficient of restitution to the normal component
- Tangential component remains unchanged in ideal scenarios
This approach simplifies complex collision analysis in CBSE Physics problems.
5. What is the coefficient of restitution in oblique collision?
The coefficient of restitution (e) measures how much velocity is retained after a collision along the line of impact.
- Defined as the ratio of relative velocity after collision to relative velocity before along the normal direction
- e = 1: Perfectly elastic collision
- 0 < e < 1: Partially elastic or inelastic
- e = 0: Perfectly inelastic collision
It is crucial for solving examination questions on oblique collisions.
6. Why does the tangential component of velocity remain unchanged in an oblique collision?
In an ideal oblique collision, the tangential component of velocity remains unchanged due to the absence of impulses along that direction.
- Only the normal (perpendicular) component is affected by the collision force
- Tangential component is unaffected if there is no friction or external force
This property helps simplify calculations in physics numericals and exam questions.
7. Explain the steps to solve an oblique collision problem in Physics.
To solve oblique collision questions efficiently, follow these steps:
1. Draw a diagram and mark the initial velocities and angles.
2. Resolve velocities into normal and tangential components.
3. Apply momentum conservation along both directions.
4. Use coefficient of restitution for normal components.
5. Find post-collision velocities, then recombine the components.
This structured approach ensures high accuracy in board exams and competitive tests.
8. What are some real-life examples of oblique collisions?
Oblique collisions can be seen in many daily activities and sports:
- Billiards/carom balls striking at angles
- Football (soccer) players kicking balls with angled shots
- Car accidents where vehicles collide from side angles
These examples help you visualize the concept for physics and competitive exams.
9. How does an oblique elastic collision differ from an oblique inelastic collision?
The main difference lies in energy conservation:
- Oblique elastic collision: Both momentum and kinetic energy are conserved
- Oblique inelastic collision: Only momentum is conserved; kinetic energy is lost
This distinction is crucial for answering exam numericals and theory questions.
10. What is the significance of studying oblique collisions in the Physics syllabus?
Oblique collisions are important as they:
- Help understand realistic collision scenarios in nature and technology
- Develop problem-solving skills, especially with vector resolution and momentum conservation
- Are routinely tested in CBSE, NEET, JEE, and other exams
Grasping these concepts enhances overall understanding of mechanics.

































