




How to Find Union, Intersection, and Difference of Two Sets with Examples
The topic "Union Intersection And Difference Of Sets" falls under TYPE A — Core Concept Pages, as it is a foundational part of the syllabus in JEE Mathematics. It covers essential operations on sets, crucial for understanding more advanced topics in mathematics and for problem-solving in competitive exams.
Purpose and Scope of Set Operations: Union, Intersection, and Difference
Set operations are foundational in mathematics. They enable the combination, comparison, and separation of sets based on membership. Analyzing these operations assists in describing relations, functions, and solving problems involving sets in advanced mathematics and competitive exams.
Core Idea Before Formalism: Intuitive Understanding
The union of sets combines all elements from the involved sets, ensuring duplication is avoided. The intersection identifies common elements shared by the sets. The difference extracts elements present in one set but not in another, clarifying exclusive membership.
Definitions and Standard Notation
Let $A$ and $B$ denote non-empty sets under a universal set $U$. The key set operations are:
- Union of sets
- Intersection of sets
- Difference of sets
- Complement of a set
The union of $A$ and $B$ is denoted as $A \cup B$. The intersection is $A \cap B$. The difference is $A - B$ or $A \setminus B$. The complement is $A^{c}$ or $\overline{A}$, relative to $U$.
Formal Properties and Results
The following properties hold for all subsets $A,B,C \subseteq U$.
- Commutative laws for union and intersection
- Associative laws for union and intersection
- Distributive laws
- De Morgan’s laws
- Identity elements
- Difference is not commutative
For every $A$ and $B$, $A \cup B = B \cup A$, and $A \cap B = B \cap A$ hold.
Associativity ensures $(A \cup B) \cup C = A \cup (B \cup C)$. Similarly, $(A \cap B) \cap C = A \cap (B \cap C)$.
Distributive property: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, and $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$.
De Morgan’s laws state $(A \cup B)^{c} = A^{c} \cap B^{c}$ and $(A \cap B)^{c} = A^{c} \cup B^{c}$.
For all $A$, $A \cup \varnothing = A$ and $A \cap \varnothing = \varnothing$. $\varnothing$ denotes the empty set.
$A - B$ is not generally equal to $B - A$.
Key Formulas for Union, Intersection, and Difference
For finite sets $A$ and $B$:
The number of elements in $A \cup B$ is $n(A \cup B) = n(A) + n(B) - n(A \cap B)$.
For the difference, $n(A - B) = n(A) - n(A \cap B)$.
For three sets, $n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C)$.
Worked Example 1: Direct Union Evaluation
Given $A = \{1, 2, 3, 4\}$ and $B = \{2, 4, 5, 6\}$. Find $A \cup B$.
First, combine all elements from both sets:
$A \cup B = \{1, 2, 3, 4, 2, 4, 5, 6\}$
Remove duplicates:
$A \cup B = \{1, 2, 3, 4, 5, 6\}$
Worked Example 2: Intersection of Sets
Given $A = \{3, 5, 7, 9\}$ and $B = \{5, 7, 11\}$, determine $A \cap B$.
Identify common elements:
$A \cap B = \{5, 7\}$
Worked Example 3: Difference and Complement
Let $U = \{a, b, c, d, e\}$, $A = \{b, c, d\}$, and $B = \{c, e\}$. Find $A - B$ and $A^{c}$.
First, determine $A - B$:
$A - B = \{b, d\}$
Next, $A^{c} = U - A$:
$A^{c} = \{a, e\}$
Worked Example 4: Using Set Identities
Let $A = \{1, 2, 3, 4\}$ and $B = \{3, 4, 5, 6\}$, $C = \{2, 3, 5\}$. Compute $(A \cap B) \cup (B \cap C)$.
First, find $A \cap B$:
$A \cap B = \{3, 4\}$
Next, $B \cap C = \{3, 5\}$
Now, calculate the union:
$(A \cap B) \cup (B \cap C) = \{3, 4, 5\}$
Common Student Misconceptions in Set Operations
- Confusing union with intersection
- Repeating elements in unions
- Assuming difference is commutative
- Ignoring universal set in complements
- Incorrect De Morgan application
Typical JEE Pattern for Questions on Set Operations
- Direct computation from given sets
- Application of union-intersection identities
- Problems using Venn diagrams
- Cardinality formula application
- Proof-based assertions on sets
Cartesian Product and Advanced Set Structures
The Cartesian product $A \times B = \{(a, b) \mid a \in A,\, b \in B\}$ forms ordered pairs. For example, $\mathbb{R}^2 = \mathbb{R} \times \mathbb{R}$ denotes the plane consisting of all ordered pairs of real numbers.
Representation of Set Operations Using Venn Diagrams
Venn diagrams visually illustrate the outcomes of union, intersection, and difference. Shaded regions indicate the resultant sets for each operation, aiding comprehension.
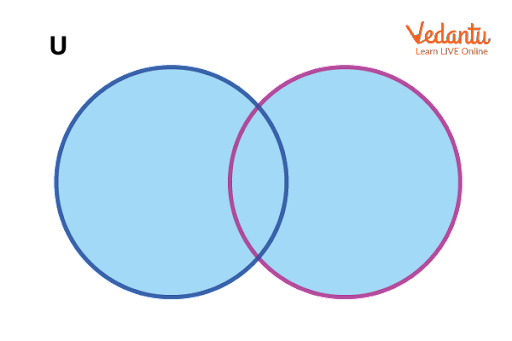
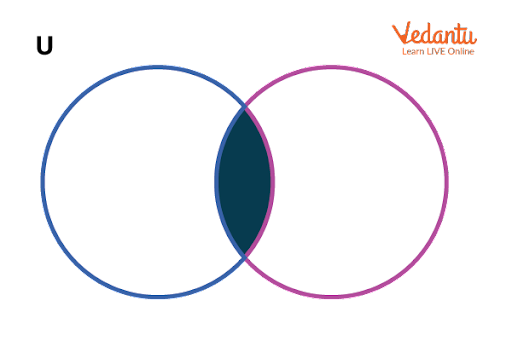
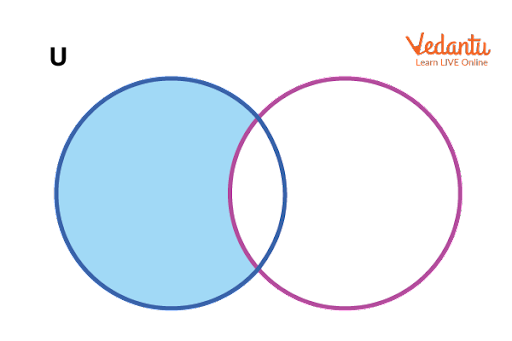
For extended study of sets, refer to Sets, Relations, And Functions, which provides foundational set theory required for JEE-level mathematics.
FAQs on Understanding Union, Intersection, and Difference of Sets
1. What is the union of sets?
Union of sets includes all elements that are present in any of the sets involved.
• The union of two sets A and B is denoted by A ∪ B.
• It contains all unique elements from both A and B.
• Mathematically, A ∪ B = {x | x ∈ A or x ∈ B}.
The concept is crucial in set theory and is commonly used in math exams and syllabus.
2. What is the intersection of two sets?
Intersection of sets refers to elements that are common to all given sets.
• The intersection of sets A and B is written as A ∩ B.
• Only those elements found in both A and B are included.
• In symbols, A ∩ B = {x | x ∈ A and x ∈ B}.
This is a fundamental concept in set operations and exam questions.
3. What is the difference of sets?
Difference of sets means elements found in one set but not in the other.
• The difference of sets A and B is written as A – B.
• It contains elements that belong to A but not to B.
• In notation, A – B = {x | x ∈ A and x ∉ B}.
This operation helps in identifying unique elements for set-based problems.
4. What are the properties of union and intersection of sets?
Union and intersection of sets follow several important properties.
Key properties include:
• Commutative Law: A ∪ B = B ∪ A; A ∩ B = B ∩ A
• Associative Law: (A ∪ B) ∪ C = A ∪ (B ∪ C); (A ∩ B) ∩ C = A ∩ (B ∩ C)
• Distributive Law: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C); A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
These help solve complex set questions in examinations.
5. Give an example of union, intersection and difference of sets.
Union, intersection, and difference show how sets relate.
Example:
• Let A = {1, 2, 3, 4} and B = {3, 4, 5, 6}
• Union (A ∪ B): {1, 2, 3, 4, 5, 6}
• Intersection (A ∩ B): {3, 4}
• Difference (A – B): {1, 2}
This example illustrates each operation using simple sets as per syllabus requirements.
6. What is the difference between subset and difference of sets?
A subset means all elements of one set are contained in another, while difference includes only elements from the first set not found in the second.
• Subset: Every element of set A is in set B (A ⊆ B).
• Difference: Elements in set A but not in set B (A – B).
Understanding this distinction is vital as it appears in many student exams and set operations problems.
7. How do you find the union and intersection of three sets?
You use logical rules to combine or compare elements of all three sets.
• Union: A ∪ B ∪ C includes all unique elements from sets A, B, and C.
• Intersection: A ∩ B ∩ C contains only those elements present in all three sets.
• List or Venn diagrams can be used for visualization and calculation.
This method is often employed for context-based and diagram problems in the syllabus.
8. What is the formula for the cardinality of union of two sets?
The cardinality of union of two sets counts the total number of elements in either set.
• Formula: n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
• n(A): Number of elements in A
• n(B): Number of elements in B
• n(A ∩ B): Number of elements in common
This important formula frequently appears in exams and set problem calculations.
9. What is a Venn diagram and how is it useful in sets?
Venn diagrams are graphical illustrations that show relationships between sets.
• They use overlapping circles to visually represent union, intersection, and difference.
• Useful for solving set problems and understanding logical relationships.
• Helpful in exam questions involving multiple sets.
Venn diagrams make set operations easier to visualize for students.
10. What is the difference between union and intersection of sets?
Union combines all elements from both sets, while intersection contains only common elements.
• Union (A ∪ B): All elements in A, B, or both
• Intersection (A ∩ B): Only elements in both A and B
This distinction is essential for solving questions involving set operations and set theory basics in the syllabus.
























