JEE Advanced 2023 Revision Notes for Electricity and Magnetism

Electric Current:

• The free electrons in an isolated metallic conductor move randomly and so the net rate of flow of charge is zero. If the potential difference is applied across the ends of that conductor, within the conductor, an electric field is set up at every point. 

• These electric fields exert force on free electrons and give them a resultant motion in a direction opposite to that of the electric field. 

• This flow of electrons is responsible for electric current. Thus, electric current can be defined as the rate of flow of charge through a conductor.

Types of Electric Current:

• Direct Current (DC): In DC, all the electrons move in the same direction, all the time that the electricity flows. Example: Current produced by the batteries in torches.

• Alternating Current (AC): In AC, the direction of the motion of the electron changes with time. Example: Power supply in-house.

Current Density: 

Current density is a vector quantity defined as the current per unit area through an infinitesimal area normal to the direction of current flow.

Drift Velocity: 

When an electric field is applied in a conductor, a force acts on each electron in the direction opposite to that of the field. The electrons start random motion. As a result, the electrons drift slowly in that direction. 

Drift velocity, $v = \dfrac{{Ee\tau }}{{2m}}$ 

$\tau$ : average time interval between two successive collisions

E: electric field

$e:$ charge on an electron

$m$ : the mass of an electron.

Therefore,

Current, $i=nAv_e$

Current density, j =$\dfrac{i}{A}$  = $nAv_e$

Ohm’s Law:

If the physical conditions of conductor (temperature, length etc.) remain constant, then the current in the conductor is directly proportional to the potential difference across the conductor.

$V~\propto~I$

$V=I~R$

Where,

R- The resistance and a proportionality constant

Combination of Resistances:

• Series Combination: $R = {R_1} + {R_2}$ 

• Parallel Combination: $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ 

Kirchhoff's Law:

• First Law (KCL): The algebraic sum of currents at any junction is equal to zero. i.e., $\sum_{i=0}^{n}~{i_n}=0$

• Second Law (KVL): The algebraic sum of potential drop across all circuit elements in a closed loop is equal to zero. i.e., $\sum_{i=0}^{n}~{V_n}=0$

Wheatstone Bridge:

It is a special type of network of resistances, commonly used for comparing resistances. It is used to find unknown resistance in terms of three known resistances. It consists of five resistances, of which four resistances are connected in the form of a bridge.

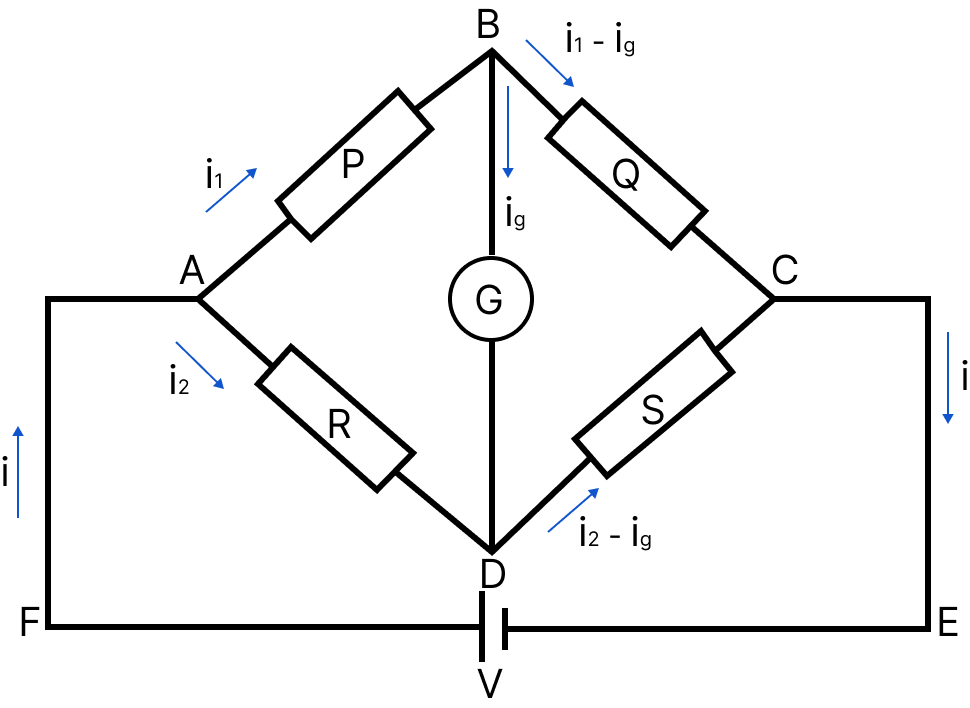
Wheatstone Bridge

For the balanced bridge, no current flows through the galvanometer.

PS = RQ

If the positions of the battery and the galvanometer are interchanged, then there will still be no deflection in the galvanometer.

Electricity:

• Electricity is concerned with the movement of electric charges.

• An electric charge is a scalar quantity with Coulomb as its unit.

• Static electricity or frictional electricity is electricity generated by friction between two bodies, such as the production of an electric charge by rubbing a plastic comb against dry hair.

Coulomb Law:

• The electrostatic force of interaction between two charge locations is proportional to the scalar multiplication of their magnitudes and inversely proportional to the square of their distance.

• The electrostatic force between two stationary charges is calculated as follows:

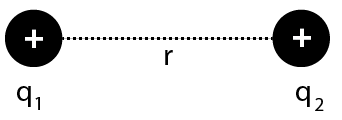
Coulomb Law

$F=\dfrac{k\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}$

Here, $k$ is proportionality constant

• In SI unit, $k$ is given by

$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}\text{N}{{\text{m}}^{2}}{{\text{C}}^{-2}}$

Here, ${{\varepsilon }_{0}}=8.85\times {{10}^{-12}}{{\text{C}}^{2}}~{{\text{N}}^{-1}}~{{\text{m}}^{-2}}$ and is called the permittivity of free space.

• i.e. $\quad F=9\times {{10}^{9}}\dfrac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}$

• The Coulomb force acts in a straight line linking the charges' locations of origin. It is spherically symmetric and Centre.

• If

${{q}_{1}}={{q}_{2}}=1\text{C}\quad \text{ and }\quad r=1~\text{m}$

Then,

$F=9\times {{10}^{9}}\dfrac{1\times 1}{{{1}^{2}}}$

$F=9\times {{10}^{9}}~\text{N}$

• We know that, One coulomb is the charge that when placed at distance of $1~\text{m}$ from another charge of same magnitude in vacuum, experiences an electric force of repulsion of magnitude$9\times {{10}^{9}}~\text{N}$.

• We know that Coulomb is a big unit, in practice we use smaller units like $\text{mC}$ or$\mu \text{C}$.

Superposition Principle

• Forces on any charge due to a number of other charges are the vector total of all the forces on that charge due to other charges, taken one at a time, according to the superposition principle.

• Due to the presence of other charges, the separate forces are unaffected.

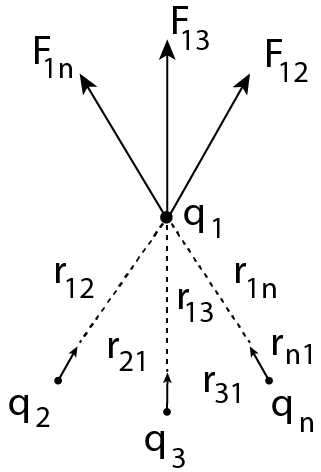
Superposition Principle

• If Consider a system of $n$point charges ${{q}_{1}},{{q}_{2}},{{q}_{3}},\ldots ,{{q}_{n}}$ be distributed in space in a discrete manner. 

• The charges are interacting with each other. 

• If  the charges be ${{q}_{2}},{{q}_{3}},\ldots ,{{q}_{n}}$ exert forces ${{\text{F}}_{12}},~{{\text{F}}_{13}},\ldots ,{{\text{F}}_{1n}}$ respectively on charge${{q}_{1}}$.

• Thus , according to the principle of superposition the total force on charge ${{q}_{1}}$ is given by

${{\text{F}}_{1}}={{\text{F}}_{12}}+{{\text{F}}_{13}}+\ldots +{{\text{F}}_{1n}}\quad \ldots \text{ (i) }$

• When  the distance between the charges ${{q}_{1}}$ and ${{q}_{2}}$ is denoted as ${{r}_{12}}$ and ${{\widehat{\mathbf{r}}}_{21}}$ is unit vector from charge ${{q}_{2}}$ to ${{q}_{1}}$, then

${{\text{F}}_{12}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{{{q}_{1}}{{q}_{2}}}{r_{21}^{2}}{{\widehat{\mathbf{r}}}_{21}}$

Therefore, the force on charge ${{q}_{1}}$ due to other charges is given by

${{\mathbf{F}}_{13}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{{{q}_{1}}{{q}_{3}}}{r_{31}^{2}}{{\widehat{\mathbf{r}}}_{31}}$

${{\text{F}}_{1n}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\cdot \dfrac{{{q}_{1}}{{q}_{n}}}{r_{n1}^{2}}{{\widehat{\mathbf{r}}}_{n1}}$

Substituting these values in Eq.(i), we get${{\text{F}}_{1}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$

$\quad \left( \dfrac{{{q}_{1}}{{q}_{2}}}{r_{21}^{2}}{{\widehat{\mathbf{r}}}_{21}}+\dfrac{{{q}_{1}}{{q}_{3}}}{r_{31}^{2}}{{\widehat{\mathbf{r}}}_{31}}+\cdots +\dfrac{{{q}_{1}}{{q}_{n}}}{r_{n1}^{2}}{{\widehat{\mathbf{r}}}_{n1}} \right)$

${{\text{F}}_{1i}}=\dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}}\sum\limits_{i=2}^{n}{\dfrac{{{q}_{i}}}{r_{i1}^{2}}}{{\widehat{\mathbf{r}}}_{i1}}$

• Due to other charges, the interaction must be on the charge that is being researched.

Heating Effect of Current:

When an electric current is passed through a conductor, the conductor becomes hot after some time and produce heat. This happens due to the conversion of some electric energy passing through the conductor into heat energy. This effect of electric current is called heating effect of current.

The heating effect of current was studied experimentally by Joule (called Joule’s law) According to the law, the heat produced (H) in a conductor is directly proportional to the product of square of current (i), resistance of the conductor (R) and the time (t) for which current is passed. Thus,

H = i2Rt

Electrical Energy and Power:

The work done in pushing a charge round an electrical circuit is given by work done = Vit

So that power, P =Vi

Biot-Savart’s Law:

Biot-Savarts law is the fundamental law of the magnetics. It gives the magnetic field by a small current element and is based on the experimental facts.

The magnetic field at a point P at a distance r, due to a small current carrying element is given by $d\overrightarrow B  = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{id\overrightarrow l  \times \overrightarrow r }}{{{r^3}}}$

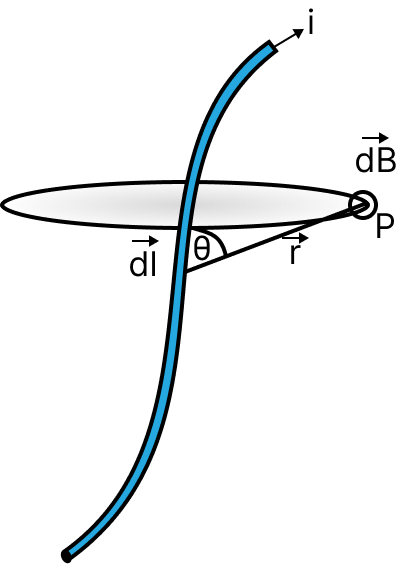
Magnetic Field

Magnetic Field Due to A Straight Current Carrying Conductor:

The magnetic field due to a straight current carrying conductor is given by $B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{i}{r}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$

Applications of Biot-Savart's Law

• Biot-Savart law use to calculate magnetic responses even at the atomic or molecular level.

• Biot-Savart law used in aerodynamic theory to calculate the velocity induced by vortex lines.

Importance of Biot-Savart Law

• Coulomb's law is similar to Biot-Savart law in electrostatics.

• Biot-Savart law is applicable for very small conductors too which carry current.

• Biot-Savart law is applicable for symmetrical current distribution.

Magnetic Field Due To A Circular Current Carrying Coil:

The magnetic field due to a circular current carrying coil is given by $B = \dfrac{{{\mu _0}}}{2}\dfrac{{{a^2}i}}{{{{\left( {{a^2} + {x^2}} \right)}^{3/2}}}}$ 

Ampere’s Law:

The line integral of the magnetic field around any closed path is equal to µ0 times the net current across the area bounded by the path.

Force on a moving charge in a magnetic field is given by, $F=q(v \times B)$.

This expression for force is obtained experimentally.

Ampere’s Circuital Law 

Ampere's circuital law states that the line integral of magnetic field induction $\vec{B}$ around any closed path in vacuum is equal to $\mu_{0}$ times the total current threading the closed path, i.e.,

Ampere’s Circuital Law 

$\oint \vec{B} \cdot \vec{d} \ell=\mu_{0} \sum I \quad$ here $\sum I=I_{1}+I_{2}-I_{3}+I_{4}-I_{5}$

The size and shape of the closed curve enclosing a current have no bearing on this outcome. The Ampere's circuital law states this.

Application of Ampere's Circuital Law:

• The following are the principal applications of Ampere's circuital law:

• The magnetic field produced by an infinitely long straight wire

$B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

• The magnetic field due to conducting rod of radius$R$ at a point at distance $r$ from the rod.$r<R,B=\left( \dfrac{{{\mu }_{o}}I}{2\pi {{R}^{2}}} \right)\cdot r$ or $B\propto r$
  
  

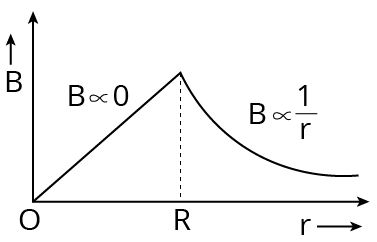
Ampere Circuit Law

1. If  $r=R$ (i.e., on the surface of the conducting rod)

    $B=\dfrac{{{\mu }_{0}}I}{2\pi R}$$(c)$r>R

    $B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

2. If $r<R$, then $B=0$

3. If $r\ge R$, then $B=\dfrac{{{\mu }_{0}}}{2\pi }\cdot \dfrac{I}{r}$

Rules to Find the Direction of Magnetic Field:

• Right Hand Palm Rule The direction of field will be perpendicular to the palm if we spread our right hand in such a way that the thumb is facing the direction of current and the fingers are facing the spot where we need to identify the direction of field.

• Maxwell's Right Handed Screw Rule When the tip of a right-handed cork screw moves in the direction of current flow through the conductor, the rotation of the screw's head gives the direction of magnetic lines of force.

Force Between Two Parallel Current Carrying Conductor:

• Two parallel linear conductors carrying currents in the same direction attract one other, while repelling each other in the opposite way.

• As a result, the force between two parallel current-carrying conductors per unit length is $F=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{2{{I}_{1}}{{I}_{2}}}{d}$

Magnetic Field of a Moving Point Charge:

• The magnetic field due to a charge$q$, moving with speed $v$ at a point $P$ at distance $r$ from the charge is given by the following formula.

$\vec{B}=\dfrac{{{\mu }_{0}}}{4\pi }\cdot \dfrac{q}{{{r}^{2}}}(\vec{v}\times \vec{r})$

Motion of Charged Particle in a Magnetic Field:

• A charged particle goes in a circular route when it enters a magnetic field perpendicularly.

• Radius of circular path, $r=\dfrac{mv}{Bq}=\dfrac{\sqrt{2m{{E}_{K}}}}{qB}$.

• Time period of particle, $T=\dfrac{2\pi m}{Bq}$.

• Frequency of particle, $n=\dfrac{Bq}{2\pi m}$.

• When a charged particle moves in the direction of a magnetic field, it is not subjected to any force.

• The velocity of a proton travelling through a magnetic field is constantly changing.

Force on a Current-Carrying Conductor in Magnetic Field:

• When a current-carrying conductor is put in a magnetic field, it is subjected to a force, which is provided by ${{F}_{m}}=\text{ Bil }\sin \theta =i\mathbf{1}\times \mathbf{B}$
  
  

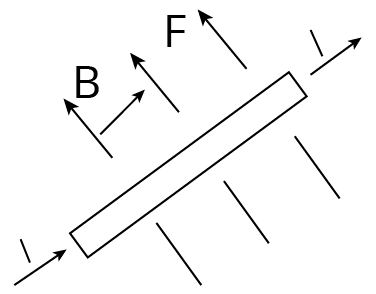
Force on a Current Carrying Conductor  

• Here , $B=$ intensity of magnetic field, $i=$ current in the conductor, $l=$ length of the conductor and $\theta =$ the angle the current makes with the magnetic field

• If, $\theta ={{90}^{{}^\circ }}$ or $\sin \theta =1$, then $F=ilB$ (Maximum)

• If , $\theta =0$ or $\sin \theta =0$

• $F=ilB\times 0=0$ The acting force is 0 when the current carrying conductor is parallel to the field.

Application of Current Carrying Conductor:

• We know that, Magnetic force acting on a current carrying conductor is not central force because$F=BIdl\sin \theta $ expression does not depends upon $r$.

• The force d F is always perpendicular to $B$ and idL.

Magnet

• Lodestone, a naturally occurring black-colored material, can attract iron items maintained nearby.

• In early days, the Greeks observed this property of loadstone an oxide called magnetite$\left( \text{F}{{\text{e}}_{3}}{{\text{O}}_{4}} \right)$. This type of substance is called a magnet.

Magnet is of Two Types:

• Natural Magnet is substances found in nature that have the property of attracting small bits of iron, which is known as magnetism.

• Artificial Magnets are magnets that have been created artificially. It has a set shape and size. for example, Horseshoe magnet

Important Facts Related to Magnet

• The life of an artificial magnet is short, whereas the life of a natural magnet is long.

• The earth's magnetism lasts an endless amount of time.

• An induced magnet is an unstable magnet.

• Magnets can be found in electric bells, fans, and washing machines, among other things.

Pole Strength

• We know that, The ability of magnetic pole to attract magnetic material is known as pole strength. It is denoted by $m$. The pole strength of North and South pole is represented by $+m$ and $-m$.

• Pole strength $(m)=\dfrac{\text{ Magnetic force }}{\text{ Magnetic induction }}=\dfrac{F}{m}$

• Ampere-meter or Newton/Tesla is the unit of pole strength.

Magnetic Axis

• The magnetic axis is the line that connects a magnet's north and south poles.

Effective Length of Magnet

• The effective length of a magnet is defined as the distance between the North Pole and the South Pole.

Magnetic Dipole

• A magnetic dipole is a magnetic north and south poles separated by a short distance.
  
  

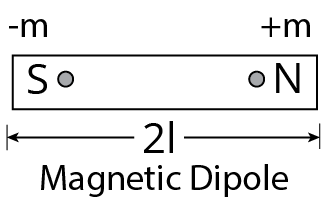
Magnetic Dipole

Magnetic Moment

• A bar magnet's magnetic moment is equal to the product of its length and pole strength. It is symbolised by  $M$. $M=(2l)\times m$

• Unit of magnetic moment is ampere-meter$^{2}$.

Magnetic Field

• A magnetic field is the area surrounding a magnet in which another magnet exerts a force on it.

Magnetic Field Lines

• Magnetic field lines are imaginary lines that depict the direction of a magnetic field.Some properties of magnetic field lines are given below.

• Magnetic line of force always from closed curves.

• They leave the North Pole and enter the South Pole externally.

• They move from the South Pole to the North Pole with in the magnet.

• They tend to contract laterally.

• The magnetic field lines never intersect each other.

Some Properties of Magnet

• Intensity of Magnetization the intensity of magnetization is defined as magnetic moment per unit volume. i.e. $I=\dfrac{M}{V}$,  Where, $M=$ magnetic dipole moment, and $\quad V=$ volume of material.

• Magnetic Permeability the magnetic permeability of a material is the measure of degree to which the magnetic field can penetrate or permeate a medium. It is denoted by $\mu $ is $\mu =\dfrac{B}{H}$. Where, $B=$ magnetic induction and $H=$ magnetizing field.

• Magnetic Susceptibility the intensity of magnetization per unit magnetizing field is known as magnetic susceptibility i.e. $\phi =\dfrac{I}{H}$Where, $I=$ intensity of magnetization and $H=$ magnetizing field.

• Relation between magnetic susceptibility and permeability the relative magnetic permeability,${{\mu }_{r}}=1+\phi $

Where, ${{\mu }_{r}}=\dfrac{\mu }{{{\mu }_{0}}}$. [${{\mu }_{0}}$=absolute permeability]

$\therefore \quad \dfrac{\mu }{{{\mu }_{0}}}=1+\phi \quad \text{ or }\quad \mu ={{\mu }_{0}}(1+\phi )$

Torque on Bar Magnet in Magnetic Field:

Torque On Bar Magnet In Magnetic Field

• In figure, a uniform magnetic field $B$ is represented by equi distant parallel line. N S is a bar magnet of length $2l$and strength of each pole is $m$. 

• The magnet is held at angle $\theta $ with the direction of $B$ Torque$(\tau )=mBl\sin \theta +mBl\sin \theta $

$\tau =2mBl\sin \theta =MB\sin \theta $

            In vector, $\tau =\vec{M}\times \vec{B}$

Work Done in Rotating a Dipole in a Magnetic Field:

• The total work done in deflecting the dipole through an angle $\theta $ from ${{0}^{{}^\circ }}$ is $W=MB(1-\cos \theta )$

• If $\theta ={{0}^{{}^\circ }}$, then $W=MB[1-1]=0$

• If $\theta ={{90}^{{}^\circ }}$, then $W=MB$

• If $\theta ={{180}^{{}^\circ }}$, then $W=2MB$, Where, $M$ is magnetic dipole moment.

Lorentz Force:

When a charged particle moves through a region of space where both electric and magnetic fields are acting, the net force on the charged particle is equal to the vector sum of the forces exert by both the fields. Thus, the net force is given by,

\[\mathbf{F}~=\text{ }q\mathbf{E}+\text{ }q\text{ }\left( \mathbf{v}~\times \mathbf{B} \right)\]

Magnetic Force On A Current Carrying Conductor:

The force on a current carrying conductor is given by \[\mathbf{F}=\text{ }i\text{ }\left( d\mathbf{l}\times \mathbf{B} \right)\]

Here dl denotes the displacement vector between the end points of the conductor.

If a circular conducting current carrying wire is placed in a uniform magnetic field, then force on it will be zero.

Electromagnetic Induction:

In 1831, Michael Faraday suggested that if electricity moving in a wire produces magnetism, then opposite might be true; a magnet moving near a wire could produce electricity. He moved a magnet in and out of a coil of wire, and electricity flowed in the coil. This is called electromagnetic induction. The electric current flows only while the magnetic field moves or varies. If the magnet and coil are still, no current flows in the coil. Electromagnetic induction is used in hundreds of machines and devices, like electric motors, generators etc. The energy needed to turn the magnet is provided by energy sources such as steam, moving water or the wind etc.

Magnetic Flux:

Magnetic flux is given by,

\[\phi \text{ }=\text{ }B.\text{ }A=\text{ }B\text{ }Acos\theta \]

Magnetic flux is a scalar quantity, but it may be negative. Its SI unit is tesla m2, which is called the weber. Thus 1 weber = 1 Wb.

Faraday’s Law of Electromagnetic Induction:

According to Faraday, whenever there is change in magnetic flux linked with the circuit, there induces an emf in the circuit. The rate of change of magnetic flux is equal to the induced emf. Thus, $e =  - \dfrac{{d\phi }}{{dt}}$ 

Here negative sign indicates that induced emf opposes the change in flux.

Lenz’s Law:

1. Lenz's law 1: Let us consider a magnet with its north pole facing a closed conducting loop moves towards it or with the south face moves away from it. When magnet moves towards the closed loop, the near face of loop becomes north, so that it repels the incoming magnet (according to Lenz’s law), and therefore the induced current in the loop will induce in counter clockwise direction. If the magnet moves away from the closed loop with its N-pole facing it, the facing side of the loop behaves like south pole and opposes the receding magnet. The direction of induced current in the loop will be clockwise.

2. Lenz's law 2: When the magnet moves with north pole towards the closed conducting loop, the flux through the loop increases, the induced current, therefore will be in such a direction; its magnetic field produces flux in opposite to the flux of the magnet. When magnet with its north pole moves away from the loop, the flux through the loop decreases. The induced current in the loop, try to compensate this decrease in flux.

Self-Induction:

Whenever there is change in magnetic flux, electromagnetic induction will take place. If there is a time varying current in a coil the magnetic field of this current will also change. And this leads to the variation of the magnetic flux through the coil, and hence to the appearance of an induced emf. Thus, the variation of current in a circuit will cause an induced emf in this circuit. This phenomenon is called self-induction.

In the absence of any ferromagnetic in the space surrounding the coil, the total flux through the coil is proportional to the current i, and we can write Nϕ = Li.

Curie's Law

• The magnetic susceptibility of a paramagnetic substance is inversely proportional to the absolute temperature, according to Curie's Law. i.e.

$\chi \propto \dfrac{1}{T}$

Curie Temperature

• When a substance reaches a specific temperature, it loses its ferromagnetic properties and begins to behave like a paramagnetic substance. 

• This temperature is referred to as the substance's curie temperature.

Magnetic Flux

• It's the total number of magnetic lines of force that pass through any surface regularly.

• When surface of area $A$ is placed perpendicular to uniform magnetic field$B$. Then, magnetic flux$\phi =BA$.

• Its unit is Wb (weber) or $\text{kg}-{{\text{m}}^{2}}/{{\text{s}}^{2}}~\text{A}$.

• No flux link will pass via a plane that is parallel to the magnetic field, and the magnetic flux link with the coil will be zero. 

• If the coil is rotated through ${{90}^{{}^\circ }}$ in the magnetic field, then magnetic flux linked with the coil is zero.

Electromagnetic Induction

• "When the magnetic flux in a closed circuit changes, an induced emf is generated in the circuit, and current is induced in the circuit as a result.

• This emf only lasts as long as the flux change does." Electromagnetic induction is the term for this phenomenon.

Faraday's Laws of Electromagnetic Induction

1. The First Law An induced emf is created in the circuit whenever the magnetic flux associated with a coil changes.

2. Second Law The negative rate of change of magnetic flux equals the induced emf.

$e=-\dfrac{\Delta \phi }{\Delta t}\text{. }$

If circuit has a coil of $N$ turns, then

$e=-\dfrac{\Delta (N\phi )}{\Delta t}$

Induced Current and Induced Charge 

• If a circuit have a resistance$(R)$, then

1. Induced current, $i=\dfrac{N}{R}\dfrac{\Delta \phi }{\Delta t}$.

2. Induced charge, $q=\dfrac{N}{R}\Delta \phi $. Where, $R=$ resistance of the circuit

Properties of Magnet:

1. Attractive Property a magnet may attract small bits of magnetic materials such as iron, steel, cobalt, nickel, and other similar metals. At poles, the attraction is greatest. Poles that are unlike one other attract each other, while poles that are similar repel each other.

2. Directive Property when suspended freely, a magnet aligns itself roughly along the geographical N-S line.

3. Magnetic Poles Exist in Pairs The S-poles of a magnet are not split when it is divided into two equal pieces transverse to its length.

Transformer

• It's a static electrical device that's used on AC circuits to step up a low voltage to a high voltage or step down a high voltage to a low value. 

• The electromagnetic induction principle governs the operation of a transformer.

Step-Up Transformer

• The primary voltage of a step-up transformer is raised to a greater level.

• Step-up transformers are those in which the number of turns on the secondary coil exceeds the number of turns on the primary coil.

Step-Down Transformer

• The primary voltage is stepped down using a step-down transformer. A step down transformer is defined as one in which the secondary coil has fewer turns than the primary coil.

• For transformer $\dfrac{{{I}_{S}}}{{{I}_{P}}}=\dfrac{{{V}_{P}}}{{{V}_{s}}}=\dfrac{{{N}_{P}}}{{{N}_{S}}}=k$

• Here, ${{I}_{p}}$ and ${{I}_{S}}=$ current in primary and secondary coil.

• ${{V}_{P}}$ And ${{V}_{S}}=$ potential in primary and secondary coil.

• ${{N}_{p}}$ And ${{N}_{S}}=$ Number of turns in primary and secondary.

Alternating Current

• Alternating current is a current whose magnitude and direction fluctuate over time and then repeat with the same magnitude and direction after a fixed length of time. 

• Equation of alternating current is $I={{I}_{0}}\sin \omega t$

• Here, ${{I}_{0}}=$ peak value of $\text{AC}$ And $\omega =$ angular frequency of $\text{AC}$

Alternating Voltage

• Alternating voltage is a voltage whose amplitude and direction fluctuate over time and then repeat with the same magnitude and direction after a set amount of time. 

• Equation of alternating voltage is $V={{V}_{0}}\sin \omega t$

Mean Value of AC

• Mean value for half-cycle of $\text{AC}$ is given by ${{I}_{m}}\text{ }=\dfrac{2{{I}_{0}}}{\pi }$ $\text{ or }\quad {{I}_{m}}\text{ }=0.637{{I}_{0}}$

• For complete cycle, mean value of $\text{AC}$ is zero.

Root Mean Square Value of A C

• For a complete cycle of$\text{AC}$, the root mean square value of current is called root mean square value. ${{I}_{\text{rms}}}=\dfrac{{{I}_{0}}}{\sqrt{2}}=0.707{{I}_{0}}$

• In India, electricity is distributed for home use in the form of a $220~\text{V}$ and at $50~\text{Hz}$.

Power in Alternating Circuit

1. If a circuit have only resistor then average power ${{P}_{\text{av}}}={{V}_{\text{rms}}}\times {{I}_{\text{rms}}}$

2. If a circuit have resistor and inductor, then 

$\begin{align}& {{P}_{\text{av}}}={{V}_{\text{rms}}}\times {{I}_{\text{rms}}}\cos \phi \text{ where, }\quad  \\& \cos \phi =\dfrac{R}{\sqrt{{{R}^{2}}+{{\omega }^{2}}{{L}^{2}}}} \\\end{align}$

3. If a circuit have only inductor or capacitor, then P_{a $v=0$.

Choke Coil

• A choke coil is a device that regulates the current in an AC circuit. The power loss in a choke coil is small.
  
  

Magnetic Declination

• The angle between true north and magnetic north is known as magnetic declination. 

• On the horizontal plane, true north is never in the same place and varies based on the location on the earth's surface and the passage of time.

Magnetic Inclination

• The angle of dip is another name for the magnetic inclination. It's the angle formed by the horizontal plane on the surface of the earth. At the magnetic poles, the magnetic inclination is 90 degrees, and at the magnetic equator, it is zero degrees. 

• At the magnetic equator, the angle of dip is ${{0}^{{}^\circ }}$ and at the magnetic poles, the angle of dip is ${{90}^{{}^\circ }}$.

Horizontal Component of the Earth's Magnetic Field

• The intensity of the earth's magnetic field is explained by two factors:

1. Horizontal component (H)

2. Vertical component (v)

$\tan \delta =\dfrac{{{B}_{v}}}{{{B}_{H}}}$

$\sin \delta =\dfrac{{{B}_{v}}}{B}$

$\cos \delta =\dfrac{{{B}_{H}}}{B}$

${{\sin }^{2}}\delta +{{\cos }^{2}}\delta =\dfrac{B_{H}^{2}}{{{B}^{2}}}+\dfrac{B_{v}^{2}}{{{B}^{2}}}$

$1=\dfrac{B_{H}^{2}}{{{B}^{2}}}+\dfrac{B_{v}^{2}}{{{B}^{2}}}$

$B=\sqrt{B_{H}^{2}+B_{v}^{2}}$

Formula Chart:

Example 1: A coil of area $500~\text{c}{{\text{m}}^{2}}$ having 1000 turns is put perpendicular to a magnetic field of intensity$4\times {{10}^{-5}}~\text{Wb}/{{\text{m}}^{2}}$. It is rotated by ${{180}^{{}^\circ }}$ in $0.1~\text{s}$, the induced emf produced is

(a) $60\text{mV}$

(b) $40\text{mV}$ 

(c) $50\text{mV}$

(d) $70\text{mV}$

Answer: b

Explanation:

According to question given that, $A=500~\text{c}{{\text{m}}^{2}},N=1000$ turns

$B=4\times {{10}^{-5}}~\text{Wb}/{{\text{m}}^{2}},\theta ={{180}^{{}^\circ }}$

and $t=0.1~\text{s},e=$ ?

$\therefore \quad e\text{ }=\dfrac{-NBA\left( \cos {{\theta }_{2}}-\cos {{\theta }_{1}} \right)}{\Delta t}$

$=\dfrac{-1000\times 4\times {{10}^{-5}}\times 500}{\left( \cos {{180}^{{}^\circ }}-\cos {{0}^{{}^\circ }} \right)\times {{10}^{-4}}}$

$=4\times {{10}^{-2}}~\text{V}=40\text{mV}$

Example 2:Which one among the following properties of a proton may change, while it moves freely in a magnetic field? 

(a) Speed

(b) Charge

(c) Mass

(d) Velocity

Answer: D

Explanation:

Electric charge is a property of matter that is responsible for electrostatic force. A proton is a charged particle with a positive charge. The magnetic field of a magnet is defined as the region around a magnet in which the magnetic force can be felt by any other magnet or magnetic material. Magnetic force on any moving charged particle $(\text{F})=q\vec{V}\times \vec{B}$

Here q is a charge, $\vec{V}$ its velocity vector, and $\vec{B}$ is magnetic field vector

$\vec{V}\times \vec{B}$ is the cross product of velocity vector and magnetic field vector

Magnetic force on any moving charged particle $(\text{F})=q\vec{V}\times \vec{B}$ Since magnetic force is in the direction of the cross product of velocity and magnetic field which is perpendicular to the velocity of the charged particle. The magnetic force acting on any moving charged particle is perpendicular to the particle's velocity. 

As a result, the magnetic force has no effect on the magnitude of velocity. It only alters the velocity's direction. Because the velocity's magnitude is equal to its speed. In a magnetic field, the speed of a moving charge particle remains constant. 

As a result, option 1 is incorrect. The mass of an object is another constant property. As a result, option 3 is correct. The fee stays the same as well. As a result, option 2 is incorrect. The velocity changes as the direction of travel changes. As a result, option 4 is correct.

Importance of Physics Electricity and Magnetism

This chapter introduces the advanced concepts of electricity. It describes how electrons flow and form an electrical current. This chapter will also explain what electromotive force is and how to determine using scientific formulas.

The basic and advanced principles of electricity will be taught to explain how engines work and how a light bulb runs on this energy. The concept of direct and alternate current will also be explained along with conductors and insulators.

On proceeding further, students will also learn what magnetism is and how it can be calculated. There are various rules and laws that explain the effect of magnetism and magnetic force in conductors. This chapter will also explain how this non-contact force acts on magnetic substances.

Moreover, this chapter will explain how electricity and magnetism are related and differ from each other. JEE Advanced Physics Electricity and Magnetism will explain the relationship between magnetism and moving charges.

The importance of this chapter can be determined by the concepts of two fundamental topics of Physics described here. Conceptual questions from this chapter come on a regular basis in the JEE Advanced exam. Preparing this chapter will ensure a good score in the competitive exam.

Benefits of Vedantu’s Electricity and Magnetism JEE Advanced Notes

• These revision notes are designed to offer a simplified version of all the concepts, scientific principles, definitions, laws, and derivations for your better understanding. These notes will help you prepare this chapter faster. You can save time by using this concise version of the chapter.

• After completely preparing this chapter, you can use these notes to revise it better. The use of these notes will help you cover it in a shorter time span. Make your study and revision sessions more productive.

• Understand the principles better and learn how to solve questions related to electricity and magnetism. Focus on sample questions given in the notes and follow the solutions given. Learn how the experts have explained the solutions to find out how to correctly answer these questions.

• Evaluate your preparation level and find out where you need to focus on more using the Electricity and Magnetism JEE Advanced notes. Make your preparation fortified and gain more confidence.
  
  

Download Electricity and Magnetism Revision Notes for JEE Advanced Free PDF

Get the free PDF version of these revision notes and complete your study material for this chapter. Refer to the notes at your convenience and understand the concepts faster. Get better insights from the lectures of the subject matter experts on these topics on YouTube and use these notes to recall what you have studied. Remember the laws, formulae, equations, and derivations of this chapter using these notes.

Important Related Links for JEE Main and JEE Advanced