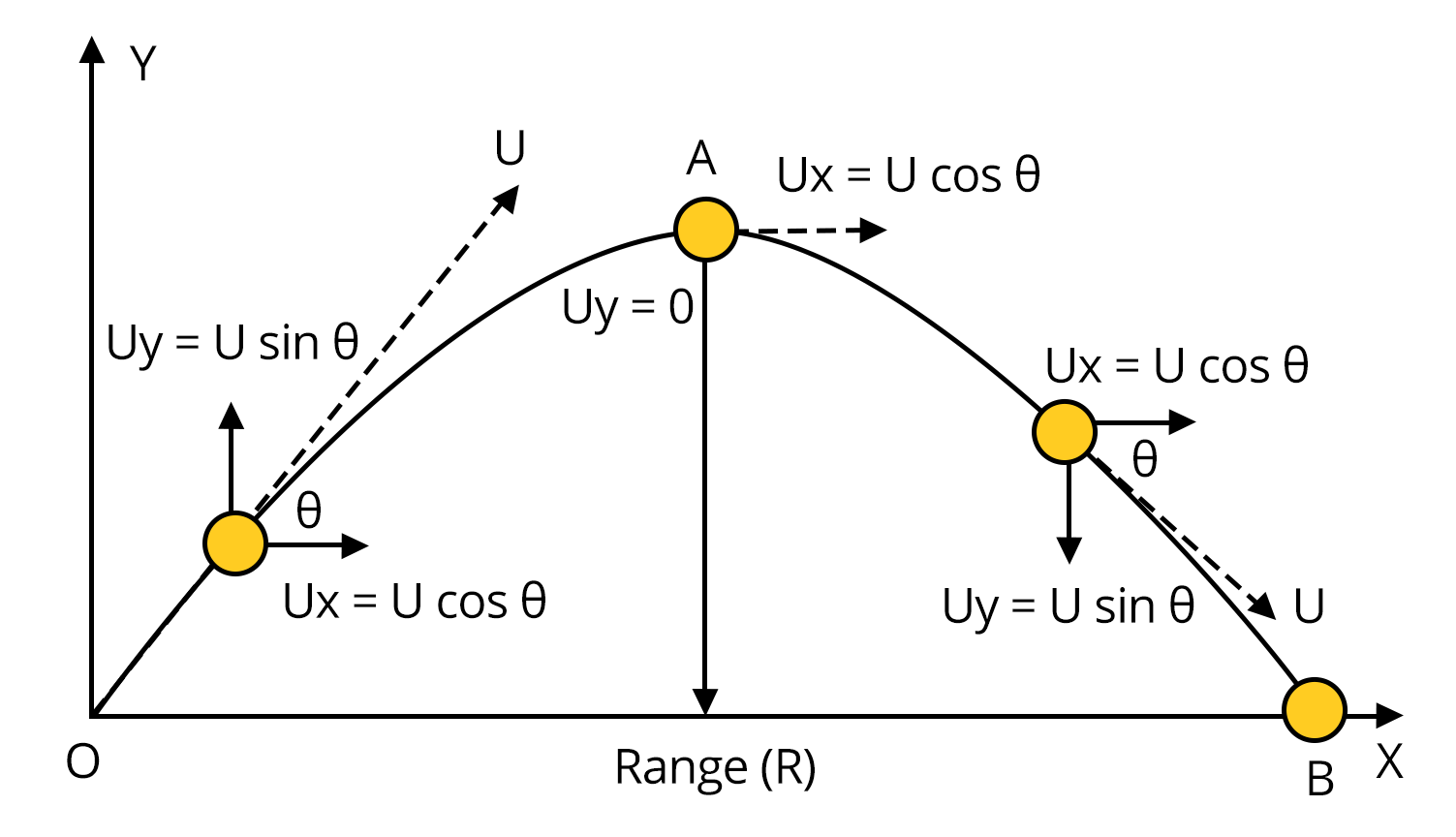
Concepts of Mechanics for JEE Advanced Physics
Mechanics is a branch of physics that deals with energy and forces and their effect on bodies. As far as JEE Advanced exam is concerned, this chapter covers a vast amount of topics and is thus a very important chapter. This chapter requires conceptual understanding as well as numerical skills to score good marks in JEE Advanced.
In Mechanics, we learn about one dimensional and two dimensional and practical applications of newton’s laws of motion and force system in mechanics. Concepts related to kinetic energy and potential energy are also discussed in detail along with the work-energy theorem.
Problems related to rotational dynamics and gravitation are also important in Mechanics. Concepts related to the properties of solids and liquids as well as thermodynamics are included in this chapter mechanics.
Now, let us see what is mechanics, mechanics definitions, laws of mechanics, important concepts and formulae related to JEE advanced exams along with a few solved examples.
JEE Advanced Physics Chapters 2026
Important Topics of Mechanics Chapter
Motion along two dimension
Laws of motion
Mass Pulley system
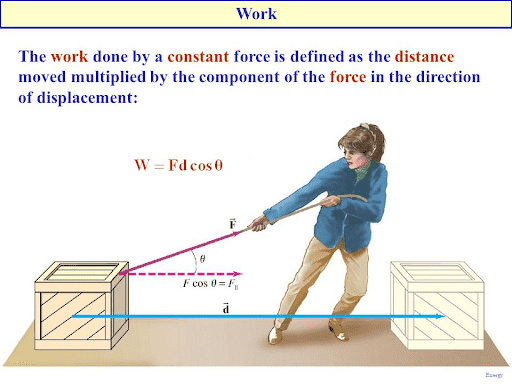
Work done by a constant force and variable force
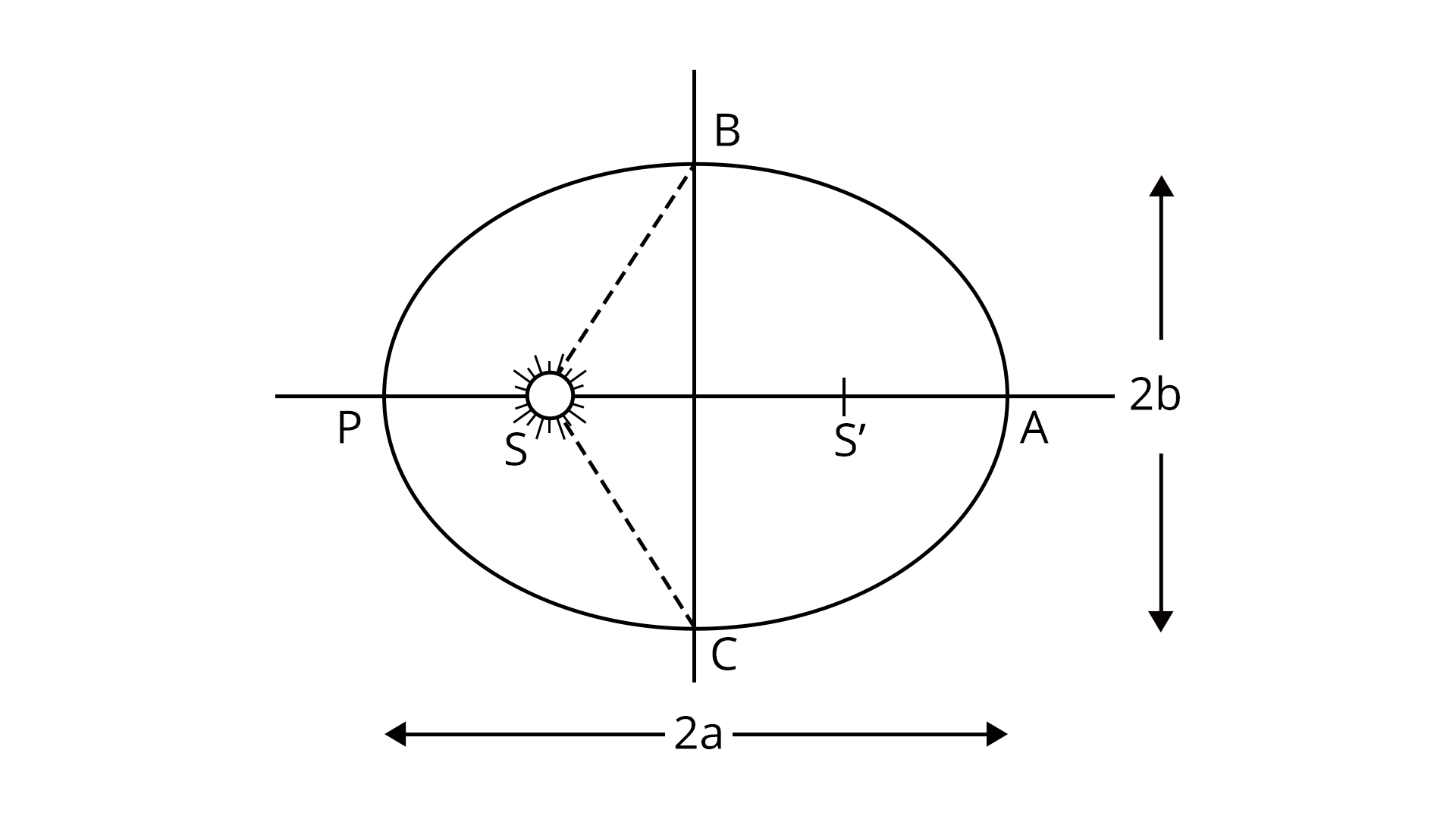
Kepler’s Law of planetary motion
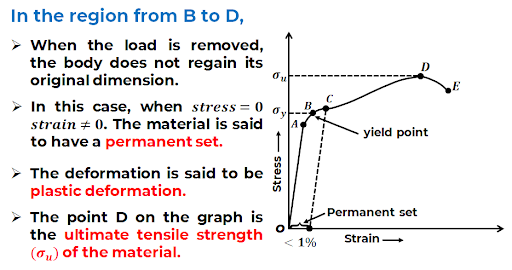
Stress-strain curve
Rotational motion
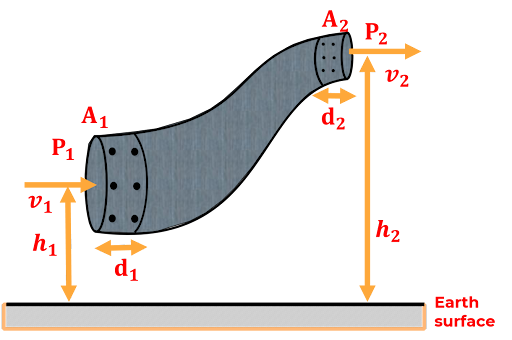
Bernoulli’s theorem
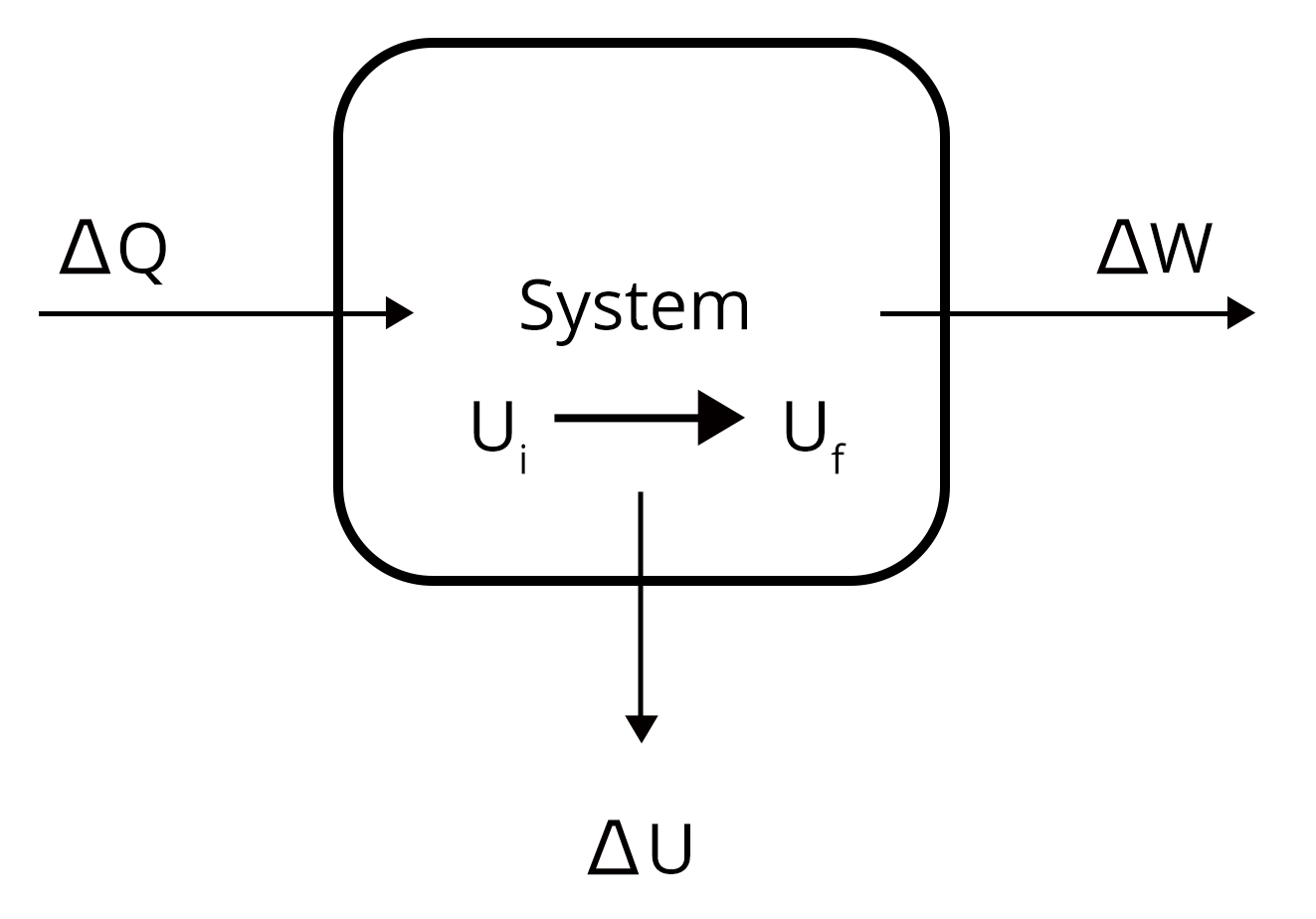
Laws of thermodynamics
Mechanics Important Concept for JEE Advanced
Mechanics is divided into three following categories:
Statistical mechanics
Classical mechanics
Quantum mechanics
Statistical Mechanics
The word static in statistical means stable or at rest. So, statistical mechanics deals with the static objects on which the force is applied. Statistical mechanics combines the principles of statistics with both classical and Quantum Physics.
In today’s era, one of the fundamental concepts (pillars) of Modern Physics is statistical mechanics. Statistical mechanics that treats and explains classical thermodynamics is statistical thermodynamics.
Let’s say, there is ‘N’ number of system of particles in thermal equilibrium at absolute temperature T, the energy E is associated with each particle, then the energy for ‘N’ particles will be:
N (E) = g (E) f (E)
Where,
N (E) = total energy of all the particles in a system.
g (E) = Number of state of energy (E) or the statistical weight regarding the energy
We call f (E) the distribution function.
f (E) has two more meanings:
It is the average number of particles in each state of energy (E).
Probability/chance of occupancy of each state of energy (E).
Statistical mechanics help us determine how macroscopic properties, viz: temperature and pressure are related to macroscopic properties that keep on varying on an average.
As we know classical thermodynamics can only measure and tabulate the quantities (heat capacity) of certain materials; however, statistical mechanics connects these thermodynamic quantities to microscopic behavior.
Classical Mechanics
Classical mechanics deals with the objects in motion under the influence of a force or the equilibrium bodies whose all forces are balanced.
We can think of classical mechanics as the explanation of basic postulates of Isaac Newton mentioned in his book named Philosophiae Naturalis Principia Mathematica (1687), commonly known as the Principia.
We call these postulates Newton’s laws of motion. These laws help us forecast with great accuracy a wide variety of phenomena ranging from the motion of individual particles to the interactions of highly complicated systems.
The core concepts in classical mechanics are force, mass, and motion. Newton couldn’t define both mass and force. Since then these both have been the subject of much philosophical observation for Newton. However, both of these are best known for their effects.
Applying the first law of motion, we can say that mass is a measure of the tendency of a body to resist changes in its state of motion, while the force accelerates bodies, i.e., when it is applied to the body, it changes the state of motion of the body. The interconnection between these two effects is what we call classical mechanics.
Quantum Mechanics
Quantum mechanics is the theory of science that studies the behavior of matter and light on the atomic and subatomic levels.
Quantum mechanics is the fundamental tool that helps to understand the theoretical stage and the electronic structure of chemical compounds and their mechanism, thermodynamics, chemical kinetics, and kinetics of chemical reactions.
Quantum mechanics attempts to describe and look for the properties of molecules and atoms and their constituents, viz: electrons, protons, neutrons, and many other esoteric particles such as quarks & gluons; these attributes involve the interactions of particles (at the microscopic level) with each other and with electromagnetic radiations such as light-rays, X-rays, and gamma-rays.
List of Important formulas for Mechanics Chapter
JEE Advanced Mechanics Solved Examples
1. A bomb of mass30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velcoity of 18 kg mass is 6 m/s. The kinetic energy of the other mass is ________.
Sol:
The total momentum of the bomb before and after exploision is constant.
$0=m_1v_1+m_2v_2$
$0=18\times 6+12\times v_2$
$v_2=-9~ m/s$
The kinetic energy of the mass having 12 kg is given by,
$K=\dfrac{1}{2}mv^2$
$K=\dfrac{1}{2}\times 12\times 9^2$
$K=486~J$
Therefore, kinetic energy of the other mass is 486 J
Key Point: The total momentum is conserved in the case of explosion of a bomb.
2. The instantaneous angular position of a point on a rotating wheel is given by the equation, $\theta(t)=2t^3-6t^2$ . The torque on the wheel becomes zero at ______.
Sol:
We can find the equation of angular velocity from the angular position as given below,
$\omega=\dfrac{d\theta}{dt}$
$\omega=\dfrac{d}{dt}(2t^3-6t^2)$
$\omega=6t^2-12t$
The equation for angular acceleration of the point is obtained by,
$\alpha=\dfrac{d\omega}{dt}$
$\alpha=\dfrac{d}{dt}(6t^2-12t)$
$\alpha=12t-12$
The torque becomes zero when angular acceleration becomes zero
$\alpha=12t-12$
$0=12t-12$
$t=1~s$
Therefore, torque becomes zero at t =1 s.
Key Point: Differentiating angular velocity with respect to time gives angular acceleration.
Previous Year Questions from JEE Advanced Paper
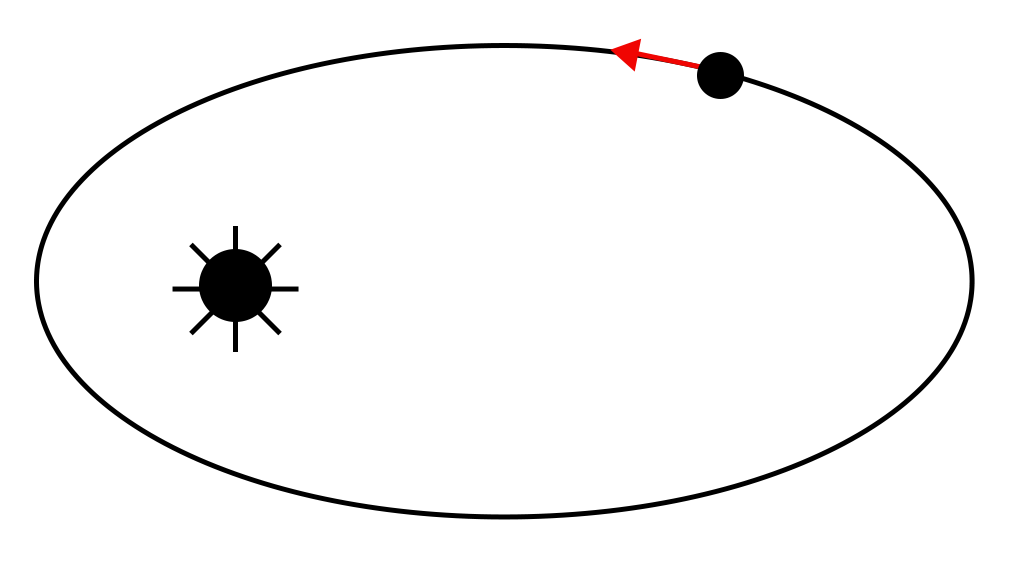
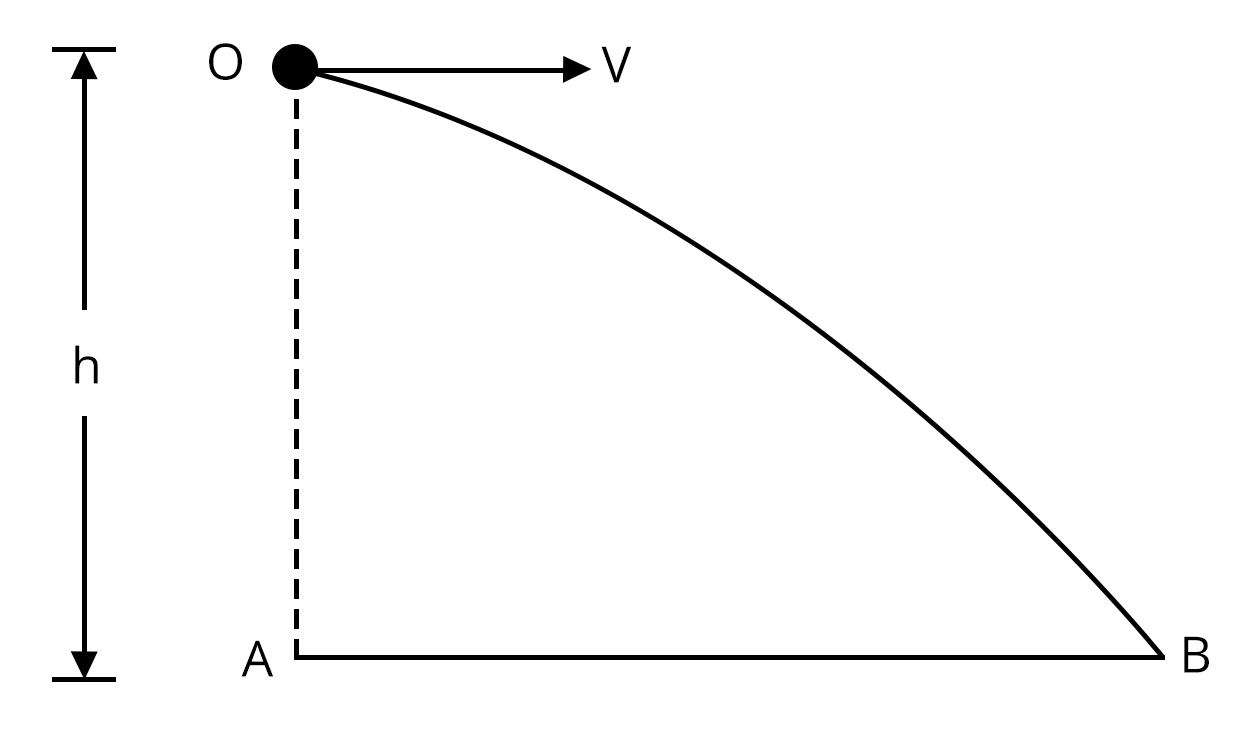
1. A wire which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on the ground as shown in the figure. The ball is released from near the top of the wire and it slides along the wire without any friction. As the bead moves from A to B, the force it applies on the wire is (JEE Advanced 2010)
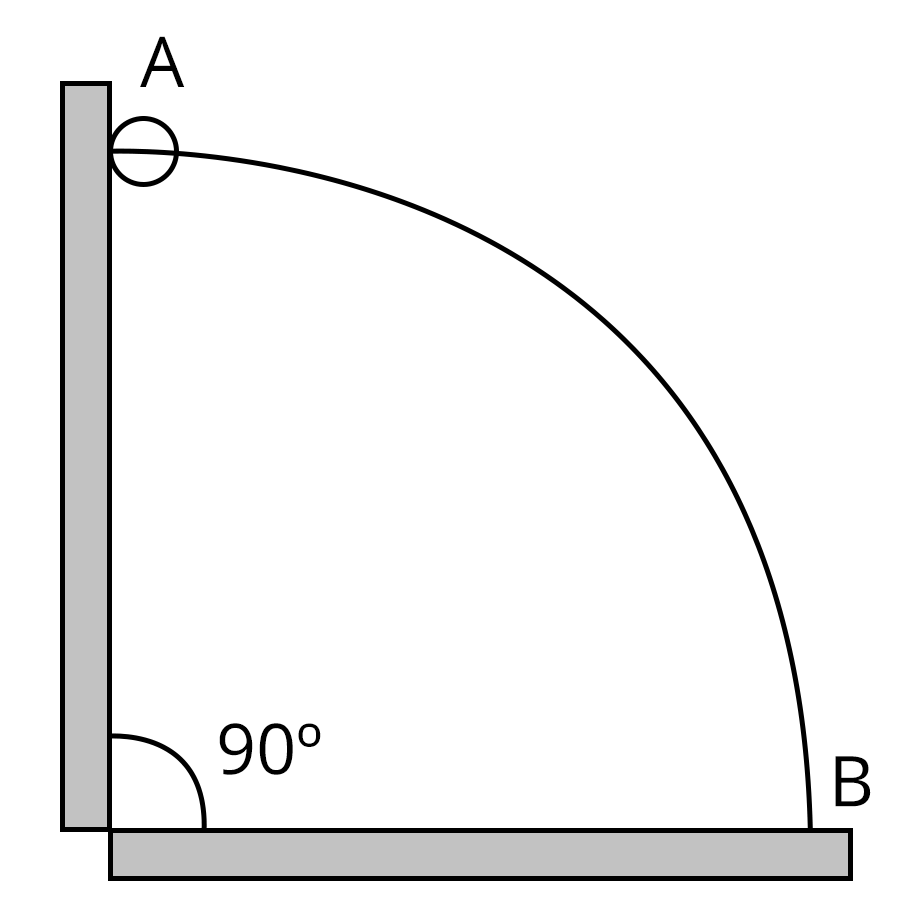
Radially outwards
Always radially inwards
Radially outwards initially and radially inwards later.
Radially inwards initially and radially outwards later.
Sol:
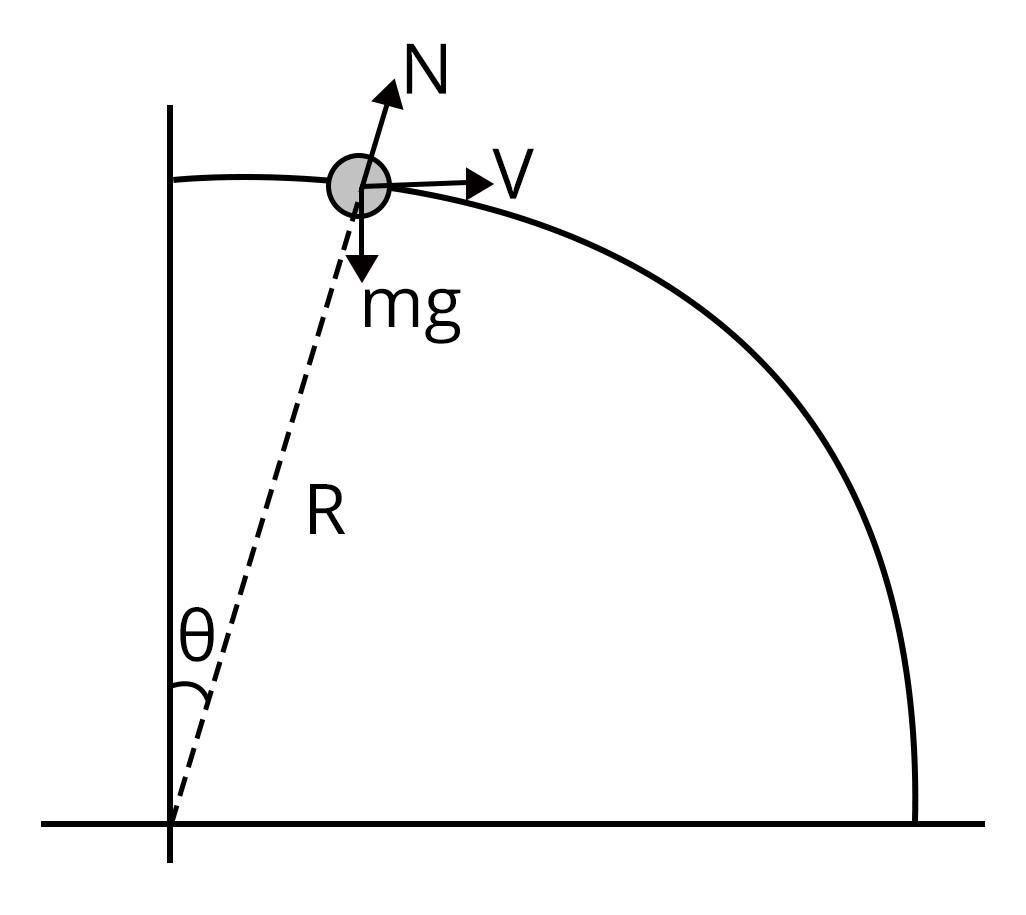
Applying newton’s second law of motion equation,
$mg\cos\theta-\dfrac{mv^2}{R}=N$...(1)
Applying conservation of energy,
$\dfrac{1}{2}mv^2=mgR(1-\cos\theta)$...(2)
Using equation (1) and (2),
$N=mg(3\cos\theta-2)$
So, N is positive when
$0\lt \theta\lt \cos^{-1}\left(\dfrac{2}3{}\right)$
N is negative when
$\theta\gt \cos^{-1}\left(\dfrac{2}3{}\right)$
Therefore, force exerted on the wire by the bead is radially inwards initially and radially outwards later. So, correct answer is option (D)
Key Point: For a body to move in a circular path, there must be a centripetal force acting on it.
2. Two identical uniform discs roll without slipping on two different surfaces, AB and CD starting at A and C with linear speeds v1 and v2 respectively, and always remain in contact with surfaces. If they reach B and D with same linear speed v1= 3 m/s and v2= ______.(JEE Advanced 2015)
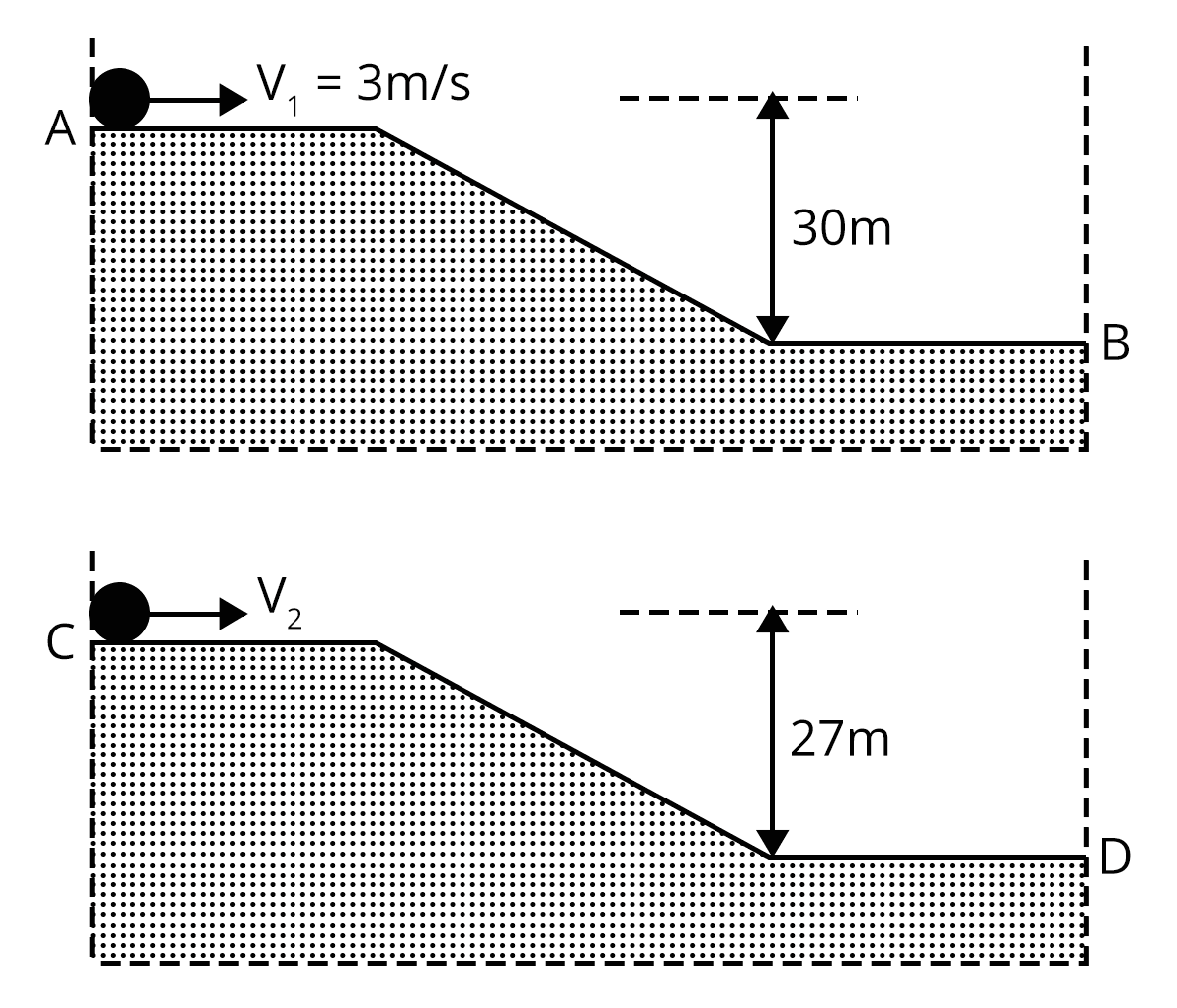
Sol:
Both discs reach B and D with same speed. Hence, final kinetic energy is same for both disc.
Applying conservation of energy,
For first disc,
$\dfrac{1}{2}I\omega_1^2+mg\times30=K$...(1)
For second disc,
$\dfrac{1}{2}I\omega_2^2+mg\times27=K$.....(2)
Solving equation (1) and equation (2), we get,
$\dfrac{1}{2}\times\left(\dfrac{3}{2}mR^2\right)\times\left(\dfrac{3}{R}\right)^2+mg\times30=\dfrac{1}{2}\times\left(\dfrac{3}{2}mR^2\right)\times\left(\dfrac{v_2}{R}\right)^2+mg\times27$
$v_2=7~m/s$
Key Point: The total mechanical energy is constant if the work is done only by the conservative force.
Practice Questions
A constant torque of 1000 Nm turns a wheel of moment of inertia 200 kgm2 about an axis through its centre. Its angular velocity after 3 seconds is (Ans: 15 rad/s)
For a satellite moving in an orbit around the earth, the ratio of kinetic energy to the potential energy is (Ans: 1:2)
JEE Advanced Physics Mechanics Study Materials
Here, you'll find a comprehensive collection of study resources for Mechanics designed to help you excel in your JEE Advanced preparation. These materials cover various topics, providing you with a range of valuable content to support your studies. Simply click on the links below to access the study materials of Mechanics and enhance your preparation for this challenging exam.
JEE Advanced Physics Study and Practice Materials
Explore an array of resources in the JEE Advanced Physics Study and Practice Materials section. Our practice materials offer a wide variety of questions, comprehensive solutions, and a realistic test experience to elevate your preparation for the JEE Advanced exam. These tools are indispensable for self-assessment, boosting confidence, and refining problem-solving abilities, guaranteeing your readiness for the test. Explore the links below to enrich your Physics preparation.
Conclusion
In the realm of JEE Advanced, the chapter on Mechanics stands as a pillar of scientific principles and problem-solving prowess. It unravels the laws that govern motion and forces in the physical world. Mechanics forms the backbone of physics, engineering, and countless scientific disciplines. A deep understanding of this chapter not only paves the way for success in the examination but also fosters a profound appreciation of the fundamental principles that shape our understanding of the universe. Aspiring students venture into a realm where abstract concepts transform into practical solutions, creating a solid foundation for advanced studies and real-world applications.
FAQs on Mechanics Chapter - Physics JEE Advanced
1. What is the weightage of mechanics in JEE Advanced?
Nearly 25% questions are asked in the JEE Advanced exam from this chapter. Mechanics is one of the most important topics and fundamental topic in JEE Advanced.
2. What is the difficulty level of Mechanics in JEE Advanced exam?
Theory of Mechanics is a vast topic and one of the fundamentals of physics required for JEE advanced. The mixed concepts from different types of mechanics topics can also asked by relating to other topics of JEE Asvanced. Students who are good in mechanics can score good marks in JEE advanced. Overall, mechanics is a moderate difficult which becomes easier with proper practise and effort. It is better if yo keep mechanics of structure pdf readily available for reference.
3. Are previous year's questions Important for JEE Advanced?
Yes, previous year's JEE Advanced questions are important. Once the student is finished learning concepts and solving problems, they must go through the previous year's question papers the last 20 years to understand the test pattern and frequent questions asked in the exam.