
A block of mass rests on a rough inclined plane making an angle of $30^\circ $ with the horizontal. The coefficient of static friction between the block and the plane is $0.8$. If the frictional force on the block is $10{\text{N}}$, then find the mass of the block in ${\text{kg}}$. Take $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
A) $2.0$
B) $4.0$
C) $1.6$
D) $2.5$
Answer
122.7k+ views
Hint: As the block of mass rests on an inclined plane which makes some angle with the horizontal, the weight of the block will have components in the horizontal and vertical directions. The normal force acting on the block will be balanced by the cosine component of the weight of the block and the frictional force will be balanced by the sine component of the force.
Complete step by step answer:
Step 1: Sketch a free body diagram of the given arrangement and list the parameters given in the question.
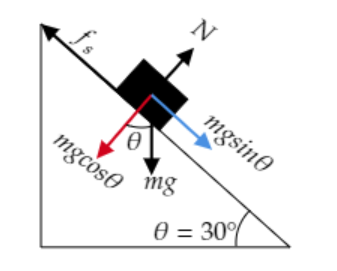
The above figure represents the block of mass $m$ resting on the rough inclined plane which makes an angle $\theta = 30^\circ $ with the horizontal.
The static friction is given to be ${f_s} = 10{\text{N}}$ .
The acceleration due to gravity is given to be $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
The coefficient of static friction is given to be ${\mu _s} = 0.8$ .
The weight of the block $W = mg$ is resolved into its cosine component $mg\cos \theta $ and its sine component $mg\sin \theta $ .
As seen from the figure, the forces acting on the block are
1. The cosine component of the weight of the block $mg\cos \theta $
2. The sine component of the weight of the block $mg\sin \theta $
3. Normal force $N$
4. Static friction ${f_s}$
Step 2: Express the force balance equation in the direction of the motion of the block to determine the mass of the block.
The force balance equation along the inclined plane is given as $mg\sin \theta = {f_s}$ .
$ \Rightarrow m = \dfrac{{{f_s}}}{{g\sin \theta }}$ -------- (1)
Substituting for ${f_s} = 10{\text{N}}$, $\theta = 30^\circ $, $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get, $ \Rightarrow m = \dfrac{{10}}{{10 \times \sin 30^\circ }} = 2{\text{kg}}$
Thus the mass of the block is $m = 2{\text{kg}}$ .
So the correct option is (A).
Note: Here the block will slide along the plane once it overcomes the static frictional force. The frictional force will be such that it opposes the motion of the block along the plane and hence will be opposite in direction to the sine component of the weight of the block. We can also obtain the force balance equation in the vertical direction as $N = mg\cos \theta $. The normal force refers to the contact force that is exerted by the plane on the block so that the block does not pass through the plane’s surface. It is a reaction to the weight of the body.
Complete step by step answer:
Step 1: Sketch a free body diagram of the given arrangement and list the parameters given in the question.

The above figure represents the block of mass $m$ resting on the rough inclined plane which makes an angle $\theta = 30^\circ $ with the horizontal.
The static friction is given to be ${f_s} = 10{\text{N}}$ .
The acceleration due to gravity is given to be $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
The coefficient of static friction is given to be ${\mu _s} = 0.8$ .
The weight of the block $W = mg$ is resolved into its cosine component $mg\cos \theta $ and its sine component $mg\sin \theta $ .
As seen from the figure, the forces acting on the block are
1. The cosine component of the weight of the block $mg\cos \theta $
2. The sine component of the weight of the block $mg\sin \theta $
3. Normal force $N$
4. Static friction ${f_s}$
Step 2: Express the force balance equation in the direction of the motion of the block to determine the mass of the block.
The force balance equation along the inclined plane is given as $mg\sin \theta = {f_s}$ .
$ \Rightarrow m = \dfrac{{{f_s}}}{{g\sin \theta }}$ -------- (1)
Substituting for ${f_s} = 10{\text{N}}$, $\theta = 30^\circ $, $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get, $ \Rightarrow m = \dfrac{{10}}{{10 \times \sin 30^\circ }} = 2{\text{kg}}$
Thus the mass of the block is $m = 2{\text{kg}}$ .
So the correct option is (A).
Note: Here the block will slide along the plane once it overcomes the static frictional force. The frictional force will be such that it opposes the motion of the block along the plane and hence will be opposite in direction to the sine component of the weight of the block. We can also obtain the force balance equation in the vertical direction as $N = mg\cos \theta $. The normal force refers to the contact force that is exerted by the plane on the block so that the block does not pass through the plane’s surface. It is a reaction to the weight of the body.
Recently Updated Pages
The ratio of the diameters of two metallic rods of class 11 physics JEE_Main

What is the difference between Conduction and conv class 11 physics JEE_Main

Mark the correct statements about the friction between class 11 physics JEE_Main

Find the acceleration of the wedge towards the right class 11 physics JEE_Main

A standing wave is formed by the superposition of two class 11 physics JEE_Main

Derive an expression for work done by the gas in an class 11 physics JEE_Main

Trending doubts
JEE Mains 2025: Check Important Dates, Syllabus, Exam Pattern, Fee and Updates

JEE Main Login 2045: Step-by-Step Instructions and Details

Class 11 JEE Main Physics Mock Test 2025

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Fluids

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




