Question

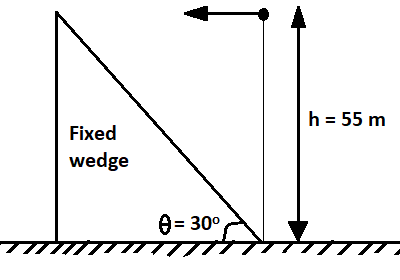
A particle is projected with a velocity $u$ in horizontal direction as shown in the figure. find $u$(approx.) so that the particle collides orthogonally with the inclined plane of the fixed wedge.

A) $10m/s$
B) $20m/s$
C) $10\sqrt 2 m/s$
D) None of these

Answer 1

Hint: In order to solve this question you have to break the velocity components of the moving particle and write the force equation and then apply the equilibrium condition. You should remember all the concepts related to wedges. Also, keep in mind that in this question the particle’s velocity component parallel to the inclined plane should be zero.

Complete step by step solution:
Considering plane along the wedge axis,
As we know that when a particle collides with the plane, its velocity component which is parallel to the inclined plane should be zero.
$ \Rightarrow u\cos \theta - g\sin \theta \times t = 0$
On further solving, we have
$ \Rightarrow t = \dfrac{u}{{g\tan \theta }}$
And also from the same equation, we get the value of u as
$ \Rightarrow u = gt \times \tan \theta $
On putting $\theta = 30^\circ $ in the above equation, we have
$ \Rightarrow u = \dfrac{{gt}}{{\sqrt 3 }}$ …….(1)
Now, consider the plane along with the x-y axis, we have
Horizontal displacement before the particle hits the plane $ = ut$
And, the vertical displacement during the t time $ = \dfrac{1}{2}g{t^2}$
Now, $\tan 30^\circ = \dfrac{{h - \dfrac{1}{2}g{t^2}}}{{ut}}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{h - \dfrac{1}{2}g{t^2}}}{{ut}}$
On solving the above equation for t, we have
$ \Rightarrow t = \sqrt {\dfrac{{6h}}{{5g}}} $
On putting the given values $h = 55m$ and $g = 9.8m/{s^2}$ we get
$ \Rightarrow t = 2.5938\sec $
Now, putting that above value of time in the equation (1), we have
$ \Rightarrow u = \dfrac{{9.8 \times 2.5938}}{{\sqrt 3 }}$
On further solving this, we get the value of the initial velocity $u$ ,
$ \Rightarrow u = 14.69 \simeq 10\sqrt 2 m/s$

Therefore, the correct option is (C).

Note: Always keep in mind that if the wedge is at rest then the problem should be solved by the normal way in which we write the force equations and applying the equilibrium conditions and if the wedge is in accelerating motion then everything will be converted into a wedge frame of reference and then solve the question by applying pseudo force.