Question

A uniform disc is acted by two equal forces of magnitude \[F\] . One of them acts tangentially to the disc, while the other one is acting at the central point of the disc. The friction between the disc surface and ground surface is \[nF\] . If \[r\] be the radius of the disc, then the value of would be (in \[N\] ):
(A) \[0\]
(B) \[1.2\]
(C) \[2.0\]
(D) \[3.2\]

Answer 1

Hint: In the given question, we have been asked to find the coefficient of the value of friction provided to us. So we have to find out the friction acting on the disc. Two forces are acting on the disc. We will use the concept of rolling of the disc, which involves the moment of inertia and the angular acceleration of the disc. We will also use the concept of force and torque equilibrium to find the required answer. How we will apply these concepts can be seen below in the detailed solution.
Formula Used: \[{{F}_{net}}=ma\] , \[\tau =I\alpha \]

Complete step by step solution:
The given question can be diagrammatically represented as given below. Refer to the figure if you have any confusions during calculations.

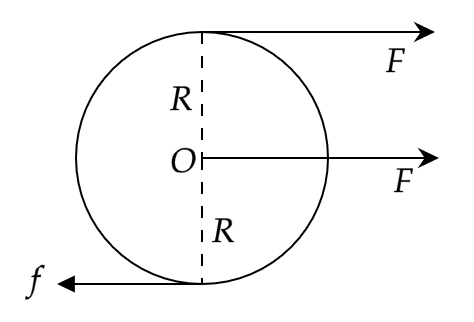
The tangential force and the force acting at the centre of the disc has been shown in the figure. The centre of the disc being denoted by O. The friction is shown acting at the point of contact of the disc with the surface. The radius of the disc is marked as R.
We can apply the force equilibrium on the disc. The equation obtained would be as follows
\[2F-f=ma--------------(1)\]
where \[a\] is the linear acceleration of the disc and \[m\] is the mass of the disc
Now some of the forces are acting at a distance from the centre of the disc, which means they will produce a net torque on the disc; the torque can be given as the product of the force and the distance of the point of the application of force from the centre or the axis of rotation.
Torque is the product of the moment of inertia of a body and the angular acceleration, that is \[\tau =I\alpha \]
The equation for the torque acting on the disc can be given as
\[(F+f)R=I\alpha \] where \[I\] is the moment of inertia of the disc and \[\alpha \] is the angular acceleration of the disc
Since we know that the moment of inertia of the disc is \[I=\dfrac{m{{R}^{2}}}{2}\] , we can substitute this value in the above equation and say that
\[\begin{align}
  & (F+f)R=\dfrac{m{{R}^{2}}}{2}\alpha \\
 & \Rightarrow F+f=\dfrac{mR\alpha }{2} \\
\end{align}\]
Since the net linear force on the body is zero, we can say that the body is undergoing pure rolling
For pure rolling, we know that \[a=R\alpha \] where the meaning of the symbols have been given above
Substituting the values stated above, we get an equation as follows
\[\begin{align}
  & F+f=\dfrac{ma}{2} \\
 & \Rightarrow 2F+2f=ma-----------(2) \\
\end{align}\]
Subtracting the equation marked one from the equation marked two, we get
\[\begin{align}
  & 3f=0 \\
 & \Rightarrow f=0 \\
\end{align}\]
Comparing this value of friction with the given value of friction in the question, we get
\[\begin{align}
  & f=nF \\
 & \Rightarrow n=0 \\
\end{align}\]

Hence we can say that option (A) is the correct answer.

Note:
Students often develop a notion that friction always means that it involves the application of weight of the body and the normal force. But in this question, we used the pure rolling concept. We knew to apply this concept by seeing the values and the data given to us. Your first approach should be to diagrammatically represent the given problem. It will simplify your solution very much.