Question

Aluminium has FCC structure. The edge length of the unit cell is 404pm If the density of the metal is $2.7gc{m^{ - 3}}$ , the molar mass (in $gmo{l^{ - 1}}$ ) of Al atom is:
A.28.20
B.30.40
C.26.80
D.25.20

Answer 1

Hint: An FCC unit cell contains atoms at all the corners of the crystal lattice and at the center of all the faces of the cube. Basically, the atom present at the face-centered is shared between two adjacent unit cells and only $\dfrac{1}{2}$ of each atom belongs to an individual cell.

Formula used:
 $d = \dfrac{{zM}}{{{N_A}{a^3}}}$
Where d is the density
M is molar mass
a is edge length
${N_A}$ is Avogadro’s number
Z is the number of formula units in the unit cell.
Complete step by step answer:
In FCC unit cells, the atoms are present in all the corners of the crystal lattice. Moreover, there is an atom present at the center of every face of the cube. The structure is as shown:

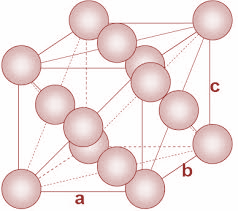
Now, in the given question, we have to calculate the molar mass Al atom. We have been given the density and the edge length of the unit cell.
Now, density is $2.7gc{m^{ - 3}}$
Edge length i.e. a is 404pm
 ${N_A}$ i.e. Avogadro number is $6.023 \times {10^{23}}$
And z for FCC is $4$
So, according to the given formula,
 $d = \dfrac{{zM}}{{{N_A}{a^3}}}$
By substituting the values, we get
 $d = \dfrac{{4 \times M}}{{6.023 \times {{10}^{23}} \times {{(404 \times {{10}^{ - 10}})}^3}}}$
 $2.7 = \dfrac{{4 \times M}}{{6.023 \times {{10}^{23}} \times {{(404 \times {{10}^{ - 10}})}^3}}}$
Therefore, $M = 26.80gmo{l^{ - 1}}$
Hence, option C is correct.

Note:The smallest replicating portion of a crystal lattice is known as a unit cell. They further exist in many types. The cubic crystal structure for example, consists of three distinct unit cell types i.e. plain cubic, face centered cubic and body centered cubic.