Question

Among the following, which should have the highest r.m.s speed at the same temperature?
A.${\text{S}}{{\text{O}}_{\text{2}}}$
B.${\text{C}}{{\text{O}}_{\text{2}}}$
C.${{\text{O}}_{\text{2}}}$
D.${{\text{H}}_{\text{2}}}$

Answer 1

Hint: To answer this question, you should recall the concept of root-mean-square speed of gas. Study the dependence of factors which affect this root mean square speed. Now use the factors to find the answer to this question.

The formula used:
${{\text{v}}_{{\text{rms}}}} = \sqrt {\dfrac{{{\text{3RT}}}}{{\text{M}}}} $ where ${{\text{v}}_{{\text{rms}}}}$=Root mean square speed, ${\text{R}}$= Universal gas constant, ${\text{T}}$= Temperature and ${\text{M}}$ is the Molar Mass of gas ---(i)

Complete Step by step solution:
We know that root mean square speed t is the square root of the average velocity-squared of the molecules in a gas. You can see that it takes into account both molecular weight and temperature, these factors directly affect the kinetic energy of a gas.
From equation (i) we can conclude that
 ${{\text{v}}_{{\text{rms}}}} \propto \dfrac{1}{{\text{M}}}$.
The molar mass will directly affect the root mean square speed.
The molar mass of each gas will be ${\text{S}}{{\text{O}}_{\text{2}}}$ = 64 g , ${\text{C}}{{\text{O}}_{\text{2}}}$ = 44 g, ${{\text{O}}_{\text{2}}}$ = 32 g, ${{\text{H}}_{\text{2}}}$ = 2 g
Out of the given options ${{\text{H}}_{\text{2}}}$ has the smallest molar mass thus, the highest r.m.s speed.
Therefore, we can conclude that the correct answer to this question is D.

Additional information: At 'higher temperature' and 'lower pressure', a gas behaves like an ideal gas, as the potential energy due to intermolecular forces becomes less significant compared with the particles' kinetic energy, and the size of the molecules becomes less significant compared to the space between them.

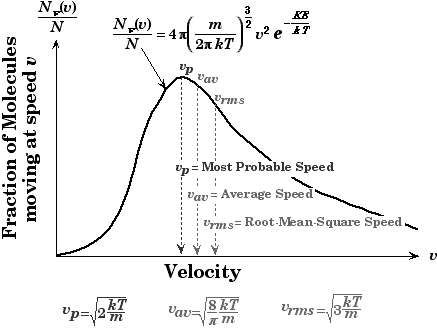
Note: Along with different speeds you should know the concept of Maxwell-Boltzmann equation. The Maxwell-Boltzmann equation helps define the distribution of speeds for gas at various temperatures. From this distribution graph function, the most probable speed, the average speed, and the root-mean-square speed can be derived. The most probable speed is the speed most likely to be possessed by any molecule in the system.