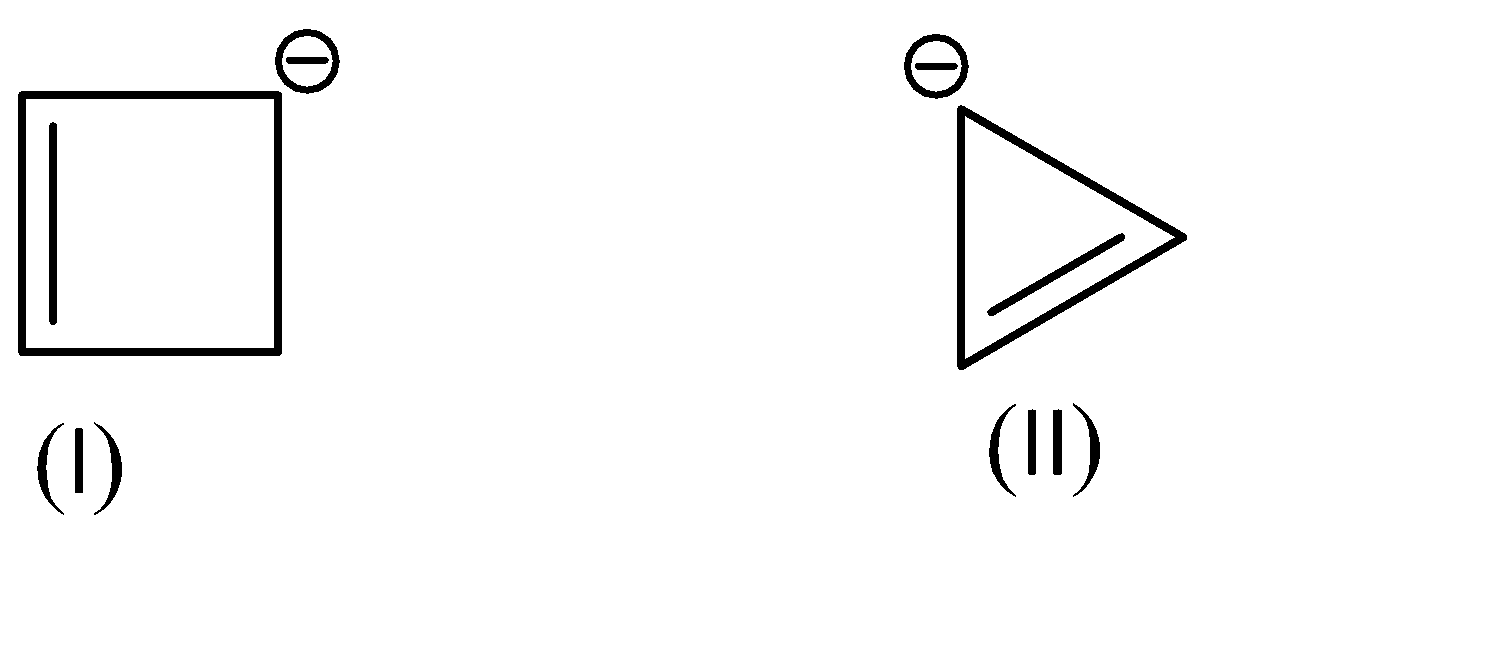Answer
110.4k+ views
Hint: Aromatic and Anti-aromatic compounds can be differentiated on the basis of Huckel's Rule.
Complete step by step answer:
We can identify the and classify compounds as either aromatic or anti-aromatic based on the following rules:
1.For a compound to be Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n+2) \[\pi \]electrons, where ‘n’ denotes the number of subsequent energy levels and can be equal to any whole number, i.e. 0,1,2,3,…
2.And for the compound to be Anti-Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n) \[\pi \]electrons
3.If a compound does not have a continuous ring of conjugated p orbitals in a planar conformation, then it is nonaromatic
One important question you must be having is how we identify \[\pi \]electrons. For that, remember the following points. \[\pi \]electrons lie in p orbitals and \[s{p^2}\]hybridized orbitals, each have 1 p orbital. In a completely conjugated molecule, each carbon atom is \[s{p^2}\]hybridized, and hence the electrons present in these p orbitals are \[\pi \]electrons.
As for the compounds given to us,
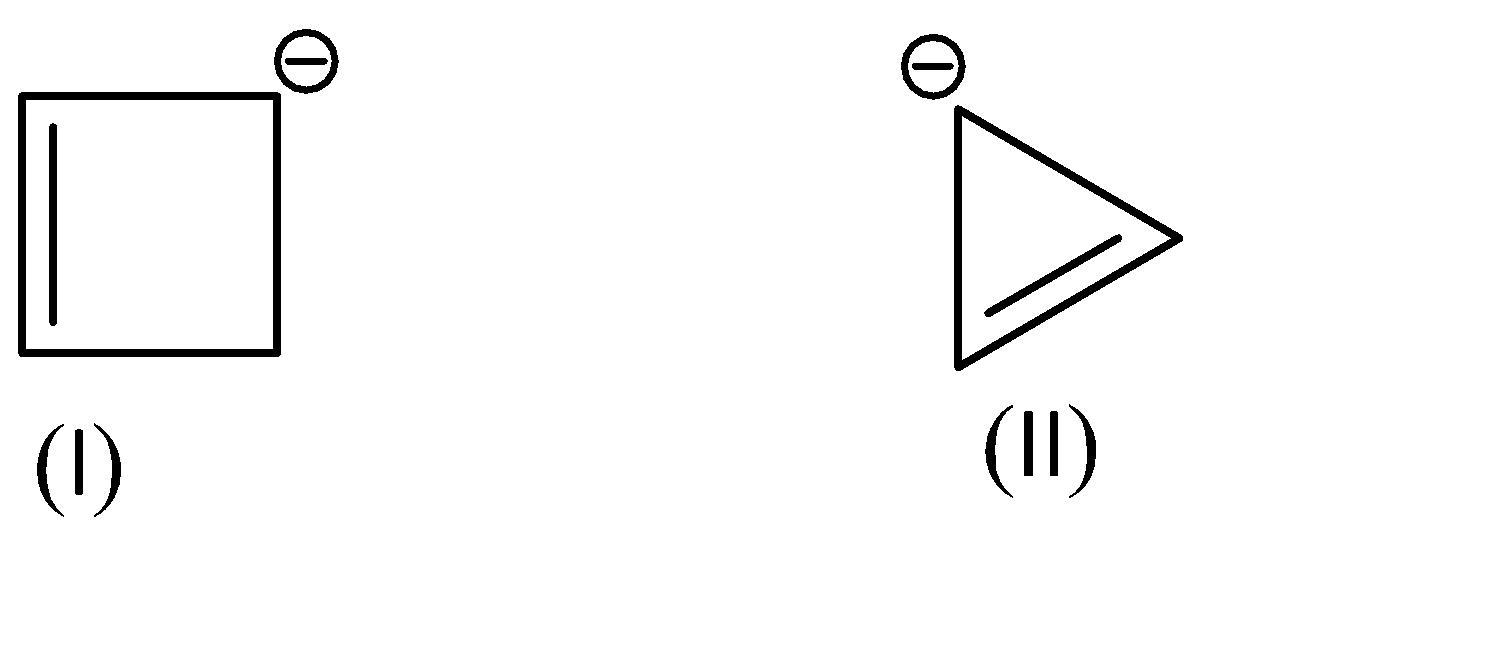
Compound (I) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.But it does not exhibit resonance

Shifting of electrons would bring us back to the same structure.
On the other hand, Compound (II) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.It does exhibit resonance
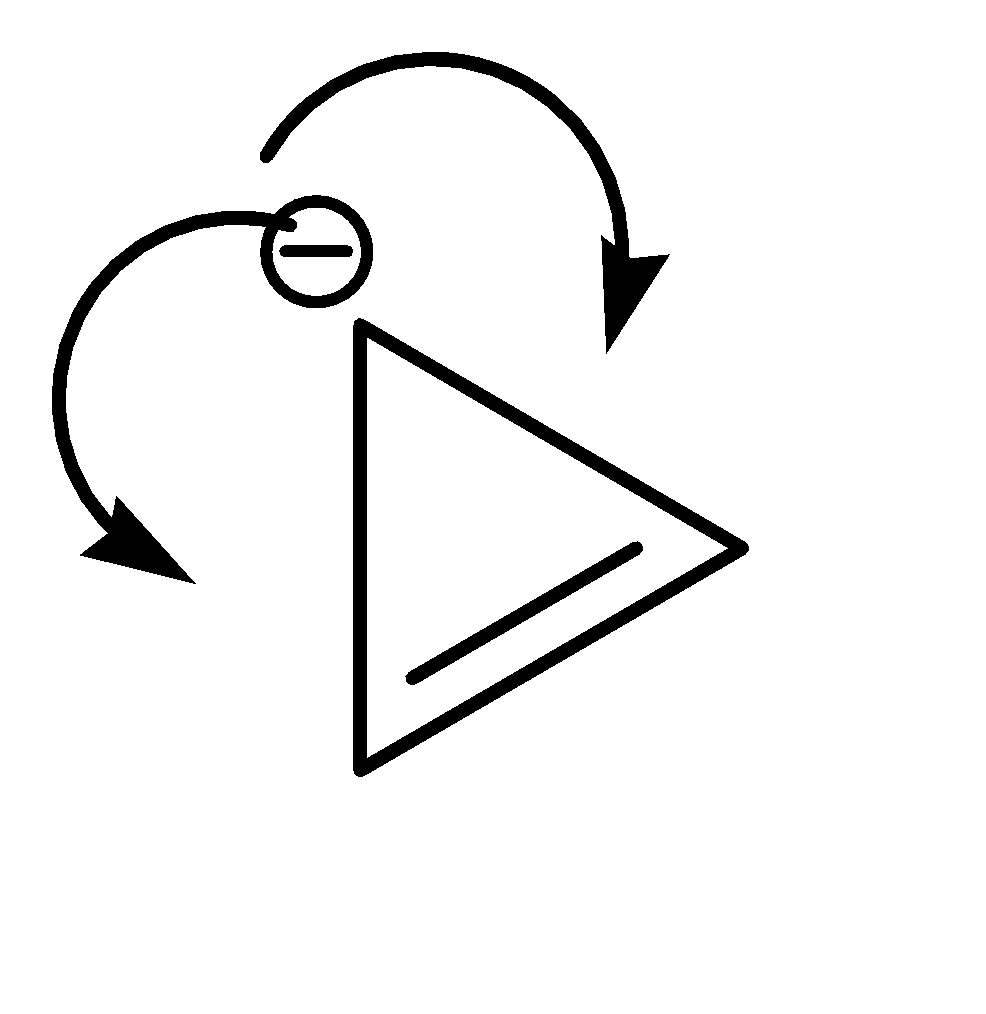
This compound exhibits resonance in both directions.
And it has 4\[\pi \]electrons, which satisfies Huckle’s rule with the value of n=1.
Hence, we can conclude that Compound (I) is Non-Aromatic and Compound (II) is Anti-Aromatic.
-We know that, the trend in the stability of Aromatic, Non-Aromatic and Anti Aromatic compounds is:
Aromatic > Non-Aromatic > Anti-Aromatic
Hence, Anti aromatic compounds are less stable than Non-aromatic Compounds. This means that the conjugate bases of Anti aromatic compounds are more stable than Non-aromatic Compounds. And we know that the increasing stability of the conjugate base increases the acidity of the compound.
Hence Anti aromatic compounds are less acidic than Non-aromatic Compounds.
\[p{K_a}\] is a method used to indicate the strength of an acid. The lower the value of \[p{K_a}\], higher is the strength of the acid.
Now, relating the above conclusions to the given compounds, we get,
\[p{K_a}\] of Compound(I) < \[p{K_a}\]of Compound (II)
Hence, both the reason and assertion are true and are interdependent.
Option A is the correct
Note:
You should not fret over finding the value of ‘n’ in Huckle’s rule because ‘n’ is not a characteristic property of any molecule. It is merely a constant which can be substituted with any natural number to satisfy the Huckel's Rule.
Complete step by step answer:
We can identify the and classify compounds as either aromatic or anti-aromatic based on the following rules:
1.For a compound to be Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n+2) \[\pi \]electrons, where ‘n’ denotes the number of subsequent energy levels and can be equal to any whole number, i.e. 0,1,2,3,…
2.And for the compound to be Anti-Aromatic, the following conditions must be satisfied
-The compound should be cyclic
-The molecular geometry of the compound should be planar
-The compound should exhibit Resonance
-The compound should obey Huckle’s rule, and hence should have (4n) \[\pi \]electrons
3.If a compound does not have a continuous ring of conjugated p orbitals in a planar conformation, then it is nonaromatic
One important question you must be having is how we identify \[\pi \]electrons. For that, remember the following points. \[\pi \]electrons lie in p orbitals and \[s{p^2}\]hybridized orbitals, each have 1 p orbital. In a completely conjugated molecule, each carbon atom is \[s{p^2}\]hybridized, and hence the electrons present in these p orbitals are \[\pi \]electrons.
As for the compounds given to us,
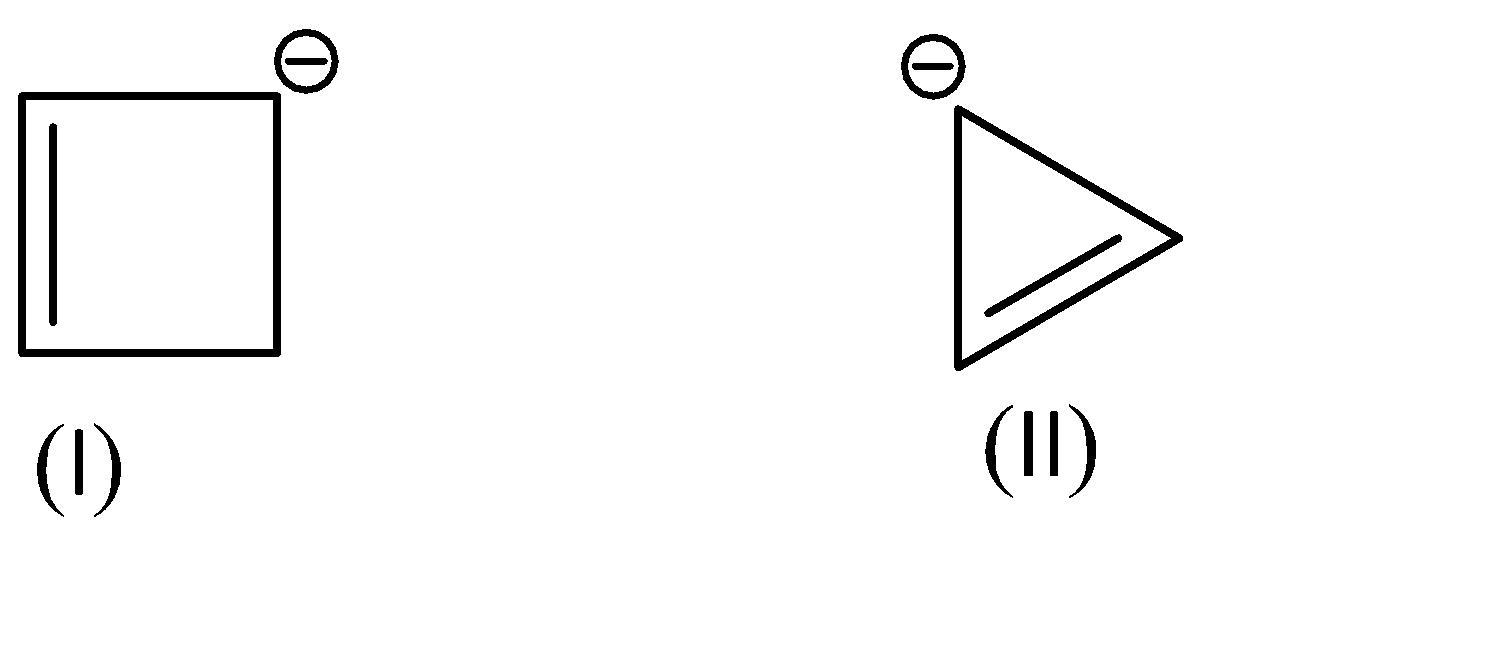
Compound (I) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.But it does not exhibit resonance

Shifting of electrons would bring us back to the same structure.
On the other hand, Compound (II) satisfies the following conditions:
1.It is a cyclic compound
2.Its molecular geometry is planar
3.It does exhibit resonance

This compound exhibits resonance in both directions.
And it has 4\[\pi \]electrons, which satisfies Huckle’s rule with the value of n=1.
Hence, we can conclude that Compound (I) is Non-Aromatic and Compound (II) is Anti-Aromatic.
-We know that, the trend in the stability of Aromatic, Non-Aromatic and Anti Aromatic compounds is:
Aromatic > Non-Aromatic > Anti-Aromatic
Hence, Anti aromatic compounds are less stable than Non-aromatic Compounds. This means that the conjugate bases of Anti aromatic compounds are more stable than Non-aromatic Compounds. And we know that the increasing stability of the conjugate base increases the acidity of the compound.
Hence Anti aromatic compounds are less acidic than Non-aromatic Compounds.
\[p{K_a}\] is a method used to indicate the strength of an acid. The lower the value of \[p{K_a}\], higher is the strength of the acid.
Now, relating the above conclusions to the given compounds, we get,
\[p{K_a}\] of Compound(I) < \[p{K_a}\]of Compound (II)
Hence, both the reason and assertion are true and are interdependent.
Option A is the correct
Note:
You should not fret over finding the value of ‘n’ in Huckle’s rule because ‘n’ is not a characteristic property of any molecule. It is merely a constant which can be substituted with any natural number to satisfy the Huckel's Rule.
Recently Updated Pages
Write an article on the need and importance of sports class 10 english JEE_Main

Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

If x2 hx 21 0x2 3hx + 35 0h 0 has a common root then class 10 maths JEE_Main

The radius of a sector is 12 cm and the angle is 120circ class 10 maths JEE_Main

For what value of x function fleft x right x4 4x3 + class 10 maths JEE_Main

Other Pages
Excluding stoppages the speed of a bus is 54 kmph and class 11 maths JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

The energy stored is a condenser is in the form of class 12 physics JEE_Main

In Searles apparatus when the experimental wire is class 11 physics JEE_Main