Question

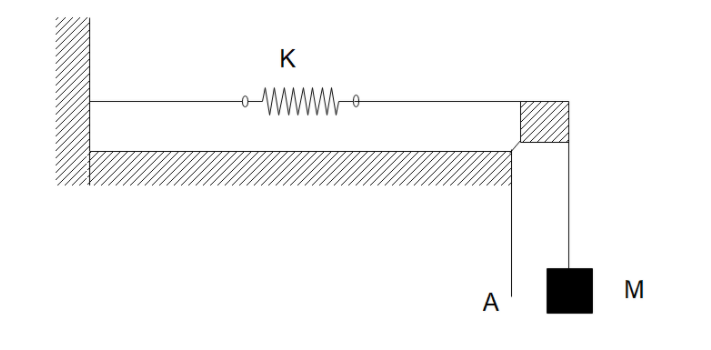
Block A in the figure is released from the rest when the extension in the spring is ${x_0}\,({x_0} < Mg/k)$. The maximum downward displacement of the block will be:

A) $\dfrac{{2Mg}}{K} - 2{x_0}$
B) $\dfrac{{Mg}}{{2K}} + {x_0}$
C) $\dfrac{{2Mg}}{K} - {x_0}$
D) $\dfrac{{2Mg}}{K} + {x_0}$

Answer 1

Hint: In this solution, we will use the law of conservation of energy. The work done by the block in moving downwards will be compensated by an increase in the potential energy of the spring.

Formula used:
In this solution, we will use the following formula:
-Potential energy of a spring: $U = \dfrac{1}{2}k{x^2}$ where \[k\] is the spring constant and $x$ is the displacement of the spring
- Potential energy due to height : \[P = mgh\] where $m$ is the mass of the object, $g$ is the gravitational acceleration, and $h$ is the change in height

Complete step by step answer:
In the figure given to us, when the block is released from rest, the block will move downwards and, in the process, it will exert extra force on the spring causing it to extend. The extension will be such that the loss in potential energy of the object due to its downwards movement will be balanced by the potential energy that will be stored in the spring due to its extension.
When the block is not released, the potential energy of the spring will be due to a displacement ${x_0}$ as $U = \dfrac{1}{2}k{x_0}^2$
Let us assume that the maximum extension of the block will be $x$. When the spring is extended, it will have potential energy of $U' = \dfrac{1}{2}k{\left( {{x_0} + x} \right)^2}$. The decrease in potential energy of the block due to moving a height $x$downwards will be \[P = - mgx\].
Then using the law of conservation of energy, we can write that
$U = U' + P$
So, we have
$\dfrac{1}{2}k{x_0}^2 = \dfrac{1}{2}k{\left( {{x_0} + x} \right)^2} - mgx$
Opening the square term on the right side, we get
$\dfrac{1}{2}k{x_0}^2 = \dfrac{1}{2}k{x_0}^2 + k{x_0}x + \dfrac{1}{2}k{x^2} - mgx$
Further simplifying, we get
$mgx = k{x_0}x + \dfrac{1}{2}k{x^2}$
Which can be written as
\[x\left( {\dfrac{k}{2}x + k{x_0} - mg} \right) = 0\]
Solving for $x$, we get
$x = 0$ or $x = \dfrac{{2mg}}{k} - 2{x_0}$

Since a zero displacement is trivial, the displacement will be $x = \dfrac{{2mg}}{k} - 2{x_0}$ which corresponds to option (A).

Note: We must be careful not to forget the potential energy associated with the initial extension of the spring when the block is not released. Also, the potential energy of the block when it moves downwards should be negative since the block will be losing potential energy when it moves downwards. Since everything will be stationary in the final state of the system as well, there will be no kinetic energy in our calculations.