For the given graph between decay rate and time find half-life (where R = decay rate)
A. \[\dfrac{{10}}{3}\ln 2\]
B. \[\dfrac{{20}}{3}\ln 2\]
C. \[\dfrac{3}{{20}}\ln 2\]
D. \[\dfrac{3}{{10}}\ln 2\]
Answer
Verified123k+ views
Hint: Radioactive reactions like the decaying of nuclei follow first-order kinetics. Here the rate constant is then depicted by the symbol λ. The rate of decay, or activity, of a species of radioactive material, is the reduction in the no.of radioactive nuclei per unit of time.
Formula Used:
\[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\];
where, R= decay rate of a reactant at a time 't'.
\[{{\rm{R}}_{\rm{o}}}\]= initial decay rate of reactant
\[{\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln2}}\]
\[{\rm{\lambda }}\]= rate constant
Complete Step by Step Solution:
The graph that is given in the question is a graph for a first-order reaction.
A reaction is called first-order if the rate of the reaction relies on one decay rate term only.
For the reaction:\[{\rm{A}} \to {\rm{B}}\]
,
the rate of reaction is directly proportional to the decay rate of A i.e., [A].
We know that for a first-order reaction,
\[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\]-----(1)
The half-life of a reaction is the time in which the decay rate of a reactant is reduced to half of its initial decay rate.
It is depicted as .
So, \[{\rm{R = }}\dfrac{{{{\rm{R}}_{\rm{o}}}}}{{\rm{2}}}\]
Putting this value in the above-mentioned equation (1), we get
Hence,
\[{\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - lnR}}\]
\[ \Rightarrow {\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = }}\dfrac{{{\rm{ln}}{{\rm{R}}_{\rm{o}}}}}{{{\rm{ln}}\dfrac{{{{\rm{R}}_{\rm{o}}}}}{{\rm{2}}}}}\]
\[ \Rightarrow {\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln2}}\]
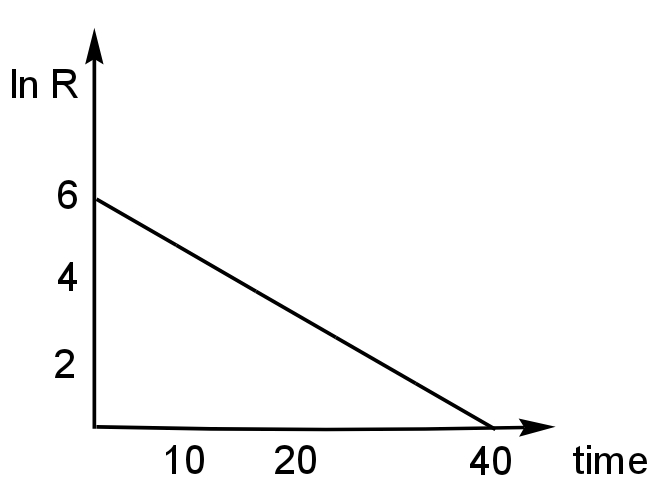
Image: Graph plotted between lnR and time
Here, in the line and is plotted against time.
The equation for the first-order reaction, which is \[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\] resembles the equation \[{\rm{y = mx + c}}\].
In this case,\[{\rm{y = lnR,x = t,m=- \lambda }}\].
So, slope, \[{\rm{m = - \lambda }}\]
Slope\[ = - \left( {\dfrac{6}{{40}}} \right) = - \left( {\dfrac{3}{{20}}} \right)\]
The slope is negative as this slope is decreasing.
\[{\rm{ - \lambda = }}\dfrac{{{\rm{ - 3}}}}{{20}}\]
So, \[{\rm{\lambda = }}\dfrac{{\rm{3}}}{{20}}\]
So, \[{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = }}\dfrac{{{\rm{ln2}}}}{{\rm{\lambda }}}\]
=\[{\rm{ln}}\dfrac{{\rm{2}}}{{\left( {\dfrac{{\rm{3}}}{{{\rm{20}}}}} \right)}}\]
= \[\dfrac{3}{{20}}\ln 2\]
So, the half-life is \[\dfrac{3}{{20}}\ln 2\].
Note: While attempting the question, one must apply the appropriate form of rate law equation for a first-order reaction. He/she has to observe the values against which the given graph is plotted. Radioactive reactions work according to first-order kinetics. Radioactivity, or radioactive decay, is the emission of a particle or a photon that is due to the breakdown of the unstable nucleus of an atom.
Formula Used:
\[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\];
where, R= decay rate of a reactant at a time 't'.
\[{{\rm{R}}_{\rm{o}}}\]= initial decay rate of reactant
\[{\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln2}}\]
\[{\rm{\lambda }}\]= rate constant
Complete Step by Step Solution:
The graph that is given in the question is a graph for a first-order reaction.
A reaction is called first-order if the rate of the reaction relies on one decay rate term only.
For the reaction:\[{\rm{A}} \to {\rm{B}}\]
,
the rate of reaction is directly proportional to the decay rate of A i.e., [A].
We know that for a first-order reaction,
\[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\]-----(1)
The half-life of a reaction is the time in which the decay rate of a reactant is reduced to half of its initial decay rate.
It is depicted as .
So, \[{\rm{R = }}\dfrac{{{{\rm{R}}_{\rm{o}}}}}{{\rm{2}}}\]
Putting this value in the above-mentioned equation (1), we get
Hence,
\[{\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - lnR}}\]
\[ \Rightarrow {\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = }}\dfrac{{{\rm{ln}}{{\rm{R}}_{\rm{o}}}}}{{{\rm{ln}}\dfrac{{{{\rm{R}}_{\rm{o}}}}}{{\rm{2}}}}}\]
\[ \Rightarrow {\rm{\lambda }}{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = ln2}}\]
Image: Graph plotted between lnR and time
Here, in the line and is plotted against time.
The equation for the first-order reaction, which is \[{\rm{lnR = ln}}{{\rm{R}}_{\rm{o}}}{\rm{ - \lambda t}}\] resembles the equation \[{\rm{y = mx + c}}\].
In this case,\[{\rm{y = lnR,x = t,m=- \lambda }}\].
So, slope, \[{\rm{m = - \lambda }}\]
Slope\[ = - \left( {\dfrac{6}{{40}}} \right) = - \left( {\dfrac{3}{{20}}} \right)\]
The slope is negative as this slope is decreasing.
\[{\rm{ - \lambda = }}\dfrac{{{\rm{ - 3}}}}{{20}}\]
So, \[{\rm{\lambda = }}\dfrac{{\rm{3}}}{{20}}\]
So, \[{{\rm{t}}_{{\rm{1/2}}}}{\rm{ = }}\dfrac{{{\rm{ln2}}}}{{\rm{\lambda }}}\]
=\[{\rm{ln}}\dfrac{{\rm{2}}}{{\left( {\dfrac{{\rm{3}}}{{{\rm{20}}}}} \right)}}\]
= \[\dfrac{3}{{20}}\ln 2\]
So, the half-life is \[\dfrac{3}{{20}}\ln 2\].
Note: While attempting the question, one must apply the appropriate form of rate law equation for a first-order reaction. He/she has to observe the values against which the given graph is plotted. Radioactive reactions work according to first-order kinetics. Radioactivity, or radioactive decay, is the emission of a particle or a photon that is due to the breakdown of the unstable nucleus of an atom.