NCERT Solutions for Class 11 Chemistry Chapter -7 Redox Reactions

1. Assign oxidation numbers to the underlined elements in each of the following species:

(a) $\mathrm{NaH}_{2} \mathrm{PO}_{4}$

Ans: P's oxidation number will be $x$.

We are aware of this.

Oxidation number of $\mathrm{Na}=+1$

Oxidation number of $\mathrm{H}=+1$

Oxidation number of $\mathrm{O}=-2$

$\begin{aligned} &(+1)(+1)(\mathrm{x})(-2) = \mathrm{NaH}_{2} \mathrm{PO}_{4} \end{aligned}$

Then there's

$1(+1)+2(+1)+1(x)+4(-2)=0$

$1+2+x-8=0$

$x=+5$

As a result, P's oxidation number is $+5$

(b) $\mathrm{NaHSO}_{4}$

$(+1)(+1)(x)(-2)$

Ans: $\mathrm{NaHSO}_{4}$

Then there's

$1(+1)+1(+1)+1(x)+4(-2)=0$

$1+1+x-8=0$

$x=+6$

As a result, S's oxidation number is $+6$

(c) $\mathrm{H}_{4} \mathrm{P}_{2} \mathrm{O}_{7}$

Ans: $\mathrm{H}_{4} \mathrm{P}_{2} \mathrm{O}_{7}$

Then, there's

$4(+1)+2(x)+7(-2)=0$

$4+2 x-14=0$

$2 x=+10$

$x=+5$

As a result, P's oxidation number is $+5$

(d) $\mathrm{K}_{2} \mathrm{MnO}_{4}$

Ans: Then, there's

$2(+1)+x+4(-2)=0$

$2+x-8=0$

$x=+6$

As a result, Mn 's oxidation number is $+6$

(e) $\mathrm{CaO}_{2}$

Ans:

Then, there's

$(+2)+2(x)=0$

$2+2 x=0$

x=-1

As a result, O's oxidation number is $-1$

(f) $\mathrm{NaBH}_{4}$

Ans: Then, there's

$1(+1)+1(x)+4(-1)=0$

$1+x-4=0$

$x=+3$

As a result, B's oxidation number is $+3$

(g) $\mathrm{H}_{2} \mathrm{~S}_{2} \mathrm{O}_{7}$

Ans: $\mathrm{H}_{2} \mathrm{~S}_{2} \mathrm{O}_{7}$

Then, there's

$2(+1)+2(x)+7(-2)=0$

$2+2 x-14=0$

$2 x=12$

$x=+6$

As a result, S's oxidation number is $+6$

(h) $\mathrm{KAl}\left(\mathrm{SO}_{4}\right)_{2} .12 \mathrm{H} 2 \mathrm{O}$

Ans: $\mathrm{KAl}\left(\mathrm{SO}_{4}\right)_{2} .12 \mathrm{H}_{2} \mathrm{O}$

Then, there's

$1(+1)+1(+3)+2(x)+8(-2)+24(+1)+12(-2)=0$

$1+3+2 x-16+24-24=0$

$2 x=12$

$x=+6$

As a result, S's oxidation number is $+6$

Because water is a neutral molecule, we can disregard it. The sum of all atoms in the water molecule's oxidation numbers can then be considered as zero. As a result of disregarding the water molecule, we now have

2. What are the oxidation numbers of the underlined elements in each of the following and how do you rationalize your results?

(a) $\mathrm{KI}_{3}$

Ans: In $K I_{3}$ K has an oxidation number (O.N.) of one. As a result, I's average oxidation number is $\dfrac{1}{3} .0 . N$, on the other hand, cannot be fractional. To determine the oxidation states, we must first study the structure of $\mathrm{KI}_{3}$.

An iodine atom makes a coordinate covalent link with an iodine molecule in a $\mathrm{KI}_{3}$ molecule.

$\overset{+1}{\mathop{{{\text{K}}^{+}}}}\,\left[ \overset{0}{\mathop{\text{I}}}\,-\overset{0}{\mathop{\text{I}}}\,\leftarrow \overset{-1}{\mathop{\text{I}}}\, \right]$

As a result, the O.N. of the two atoms that make up the $I_{2}$ molecule in a $\mathrm{KI}_{3}$ molecule is 0, whereas the $0 . N$. of the I atom that makes up the coordinate bond is $-1 .$

(b) $\mathrm{H}_{2} \mathrm{~S}_{4} \mathrm{O}_{6}$

Ans: $\text { Now, } 2(+1)+4(x)+6(+2)=0$

$\Rightarrow 2+4 x-12=0$

$\Rightarrow 4 x=10$

$\Rightarrow x=+2 \frac{1}{2}$

However, O.N. cannot be fractional. Hence, S must be present in different oxidation states in the molecule.

The O.N. of two of the four $\mathrm{S}$ atoms is $+5$ and the O.N. of the other two $S$ atoms is $0 .$

(c) $\mathrm{Fe}_{3} \mathrm{O}_{4}$

Ans: When the $O . N$. of $O$ is set to $-2$, the O.N. of $\mathrm{Fe}$ is found to be $+2 \dfrac{2}{3}$. O.N., on the other hand, cannot be fractional.

One of the three Fe atoms in this example has an O.N. of $+2$, whereas the other two $\mathrm{Fe}$ atoms have an O.N. of $+3$.

$\mathrm{FeO}^{+2} \mathrm{Fe}_{2} \mathrm{O}_{3}$

(d) $\mathrm{CH}_{3} \mathrm{CH}_{2} \mathrm{OH}$

Ans: ${x+1}-2$

$C_{2} H_{6} O$

$2(x)+6(+1)+1(-2)=0$

$2 x+6-2=0$

$x=-2$

This molecule's two carbon atoms are found in two separate settings. As a result, their oxidation numbers cannot be the same.

As a result, C has the oxidation states of -3 and -1.

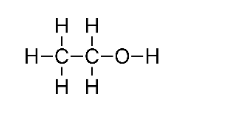
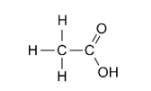
(e) $\mathrm{CH}_{3} \mathrm{COOH}$

Ans:

$x+1-2$

$C_{2} H_{4} O_{2}$

$2(x)+4(+1)+2(-2)=0$

$2 x+4-4=0$

$x=0$

The average O.N. of $C$, on the other hand, is 0 . This molecule's two carbon atoms are found in two separate settings. As a result, their oxidation numbers cannot be the same.

In $\mathrm{CH}_{3} \mathrm{COOH}, \mathrm{C}$ has the oxidation states of $+3$ and $-3$.

3. Justify that the following reactions are redox reactions:

(a) $\mathrm{CuO}(\mathrm{s})+\mathrm{H}_{2}(\mathrm{~g}) \rightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g})$

Ans: Let's write the oxidation number of each element in the reaction as follows:

$\mathrm{CuO}(\mathrm{s})+\mathrm{H}_{2}(\mathrm{~g}) \rightarrow \mathrm{Cu}(\mathrm{s})+1-2$

Cu 's oxidation number falls from $+2$ in $\mathrm{CuO}$ to 0 in $\mathrm{Cu}$, implying that $\mathrm{CuO}$ is reduced to $\mathrm{Cu} .$ In addition, the oxidation number of $\mathrm{H}$ in $\mathrm{H}_{2}$ increases from 0 to $+1$ in $\mathrm{H}_{2} \mathrm{O}$, indicating that $\mathrm{H}_{2}$ is oxidized to $\mathrm{H}_{2} \mathrm{O}$. As a result, this is a redox reaction.

(b) $\mathrm{Fe}_{2} \mathrm{O}_{3}(\mathrm{~s})+3 \mathrm{CO}(\mathrm{g}) \rightarrow 2 \mathrm{Fe}(\mathrm{s})+3 \mathrm{CO}_{2}(\mathrm{~g})$

Ans: Let's write the oxidation number of each element in the reaction as follows:

$\mathrm{Fe}_{2} \mathrm{O}_{3}(\mathrm{~s})+3 \mathrm{CO}(\mathrm{g}) \rightarrow 2 \mathrm{Fe}(\mathrm{s})+3 \mathrm{CO}_{2}(\mathrm{~g})$

Fe 's oxidation number falls from $+3$ in $\mathrm{Fe}_{2} \mathrm{O}_{3}$ to 0 in Fe, implying that $\mathrm{Fe}_{2} \mathrm{O}_{3}$ is reduced to Fe. The oxidation number of $\mathrm{C}$, on the other hand, increases from $+2$ in $\mathrm{CO}$ to $+4$ in $\mathrm{CO}_{2}$, indicating that $\mathrm{CO}$ is oxidized to $\mathrm{CO}_{2}$. As a result, the reaction in question is a redox reaction.

(c) $4 \mathrm{BCl}_{3}(\mathrm{~g})+3 \mathrm{LiAlH}_{4}(\mathrm{~s}) \rightarrow 2 \mathrm{~B}_{2} \mathrm{H}_{6}(\mathrm{~g})+3 \mathrm{LiCl}(\mathrm{s})+3 \mathrm{AlCl}_{3}(\mathrm{~s})$

Ans: Let's write the oxidation number of each element in the reaction as follows:

$4 \mathrm{BCl}_{3}(\mathrm{~g})+3 \mathrm{LiAlH}_{4}(\mathrm{~s}) \rightarrow 2 \mathrm{~B}_{2} \mathrm{H}_{6}(\mathrm{~g})+3 \mathrm{LiCl}(\mathrm{s})+3 \mathrm{AlCl}_{3}(\mathrm{~s})$

The oxidation number of $\mathrm{B}$ drops from $+3$ in $\mathrm{BCl}_{3}$ to $-3$ in $\mathrm{B}_{2} \mathrm{H}_{6}$ in this reaction. $\mathrm{BCl}_{3}$ is reduced to $\mathrm{B}_{2} \mathrm{H}_{6}$ in this way. In addition, the oxidation number of $\mathrm{H}$ in $\mathrm{LiAlH}_{4}$ increases to $-1$ in $\mathrm{B}_{2} \mathrm{H}_{6}$, indicating that LiAlH 4 is oxidized to $\mathrm{B}_{2} \mathrm{H}_{6} .$ As a result, the reaction in question is a redox reaction.

(d) $2 \mathrm{~K}(\mathrm{~s})+\mathrm{F}_{2}(\mathrm{~g}) \rightarrow 2 \mathrm{~K}+\mathrm{F}-(\mathrm{s})$

Ans: Let's write the oxidation number of each element in the reaction as follows:

$2 \mathrm{~K}(\mathrm{~s})+\mathrm{F}_{2}(\mathrm{~g}) \rightarrow 2 \mathrm{~K}+\mathrm{F}-(\mathrm{s})$

The oxidation number of $K$ increases from 0 in to $+1$ in $K F$ in this reaction, indicating that $\mathrm{K}$ is oxidized to $\mathrm{KF}$. The oxidation number of $\mathrm{F}$, on the other hand, decreases from 0 in $\mathrm{F}_{2}$ to $-1$ in $\mathrm{KF}$, indicating that $\mathrm{F}_{2}$ is reduced to $\mathrm{KF}$.

As a result, the preceding reaction is a redox reaction.

(e) $4 \mathrm{NH}_{3}(\mathrm{~g})+5 \mathrm{O}_{2}(\mathrm{~g}) \rightarrow 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$

Ans:

Let's write the oxidation number of each element in the reaction as follows:

$-3 \quad+1 \quad 0$

$4 \mathrm{NH}_{3}(\mathrm{~g})+5 \mathrm{O}_{2}(\mathrm{~g}) \rightarrow 4$ $\mathrm{NO}(\mathrm{g})+6 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$

The oxidation number of $\mathrm{N}$ rises from $-3$ in $\mathrm{NH}_{3}$ to $+2$ in $\mathrm{NO}$ in this case. The oxidation number of $\mathrm{O}_{2}$ drops from 0 in $\mathrm{O}_{2}$ to $-2$ in $\mathrm{NO}$ and $\mathrm{H}_{2} \mathrm{O}$, indicating that $\mathrm{O}_{2}$ is reduced.

As a result, the reaction in question is a redox reaction.

4. Fluorine reacts with ice and results in the change:

$\mathrm{H}_{2} \mathrm{O}(\mathrm{s})+\mathrm{F}_{2}(\mathrm{~g}) \rightarrow \mathrm{HF}(\mathrm{g})+\mathrm{HOF}(\mathrm{g})$

Justify that this reaction is a redox reaction.

Ans:

Let's write the oxidation number of each atom in the reaction above its symbol as follows:

$+1 \quad-2 \quad 0 \quad+1 \cdot 1 \quad+1 \cdot 2+1$

$\mathrm{H}_{2} \mathrm{O}(\mathrm{s})+\mathrm{F}_{2}(\mathrm{~g}) \rightarrow$$\mathrm{HF}(\mathrm{g})+\mathrm{HOF}(\mathrm{g})$

Here, we have observed that the oxidation number of $\mathrm{F}$ increases from 0 in $\mathrm{F}_{2}$ to $+1$ in HQF . Also, the oxidation number decreases from 0 in $\mathrm{F}_{2}$ to $-1$ in $\mathrm{HF}$. Thus, in the above reaction, $F$ is both oxidized and reduced. Hence, the given reaction is a redox reaction.

5. Calculate the oxidation number of Sulphur, chromium, and nitrogen in $\mathrm{H}_{2} \mathrm{SO}_{5}$, $\mathrm{Cr}_{2} \mathrm{O}_{7}{ }^{2-}$ and $\mathrm{NO}_{3}^{-}$. Suggest structure of these compounds. Count for the fallacy.

Ans: 

$\begin{array}{cc}+1 & \times-2\end{array}$

(i) $\mathrm{H}_{2} \mathrm{SO}_{5}$

$2(+1)+1(x)+5(-2)=0$

$2+x-10=0$

$x=+8$

S's O.N., on the other hand, cannot be $+8 .$ S has six electrons in its valence shell. As a result, S's O.N. cannot be greater than $+6$.

The structure of $\mathrm{H}_{2} \mathrm{SO}_{5}$ is depicted in the diagram below.

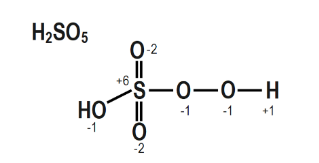
$2(\mathrm{H})+1(\mathrm{~S})+\beta(0)+2(0$ in peroxy linkage $2(+1)+1(x)+3(-2)+2(-1)=0$

$2+x-6-2=0$

$x=+6$

As a result, S's O.N. is $+6$.

(ii)

$x \quad-2$

$\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}$

$2(x)+7(-2)=-2$

$2 x-14=-2$

$x=+6$

The O.N. of $\mathrm{Cr}$ in $\mathrm{Cr}_{2} \mathrm{O}_{7}{ }^{2-}$ is not a fallacy in this case.

The structure of $\mathrm{Cr}_{2} \mathrm{O}_{7}{ }^{2-}$ is depicted in the diagram below

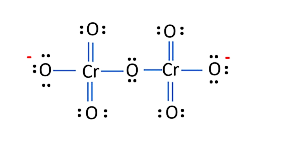
Each of the two $\mathrm{Cr}$ atoms here have an O.N. of $+6$.

(iii) $\mathrm{NO}_{3}$

$1(x)+3(-2)=-1$

$x-6=-1$

$x=+5$

The O.N. of $\mathrm{N}$ in $\mathrm{NO}_{3}^{\circ}$ is not a fallacy in this case.

The structure of $\mathrm{NO}_{3}^{\circ}$ is depicted in the diagram below

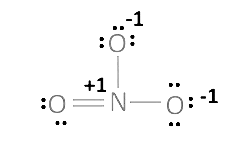
The O.N. value of the N atom is +5.

6. Write the formula for the following compounds:

(a) Mercury (II) chloride

Ans: $\mathrm{H}_{\mathrm{g}} \mathrm{Cl}_{2}$

(b) Nickel (II) sulphate

Ans: $\mathrm{NiSO}_{4}$

(c) Tin (IV) oxide

Ans: $\mathrm{SnO}_{2}$

(d) Thallium(I) sulphate

Ans: $\mathrm{Tl}_{2} \mathrm{SO}_{4}$

(e) Iron (III) sulphate

Ans: $\mathrm{Fe}_{2}\left(\mathrm{SO}_{4}\right)_{3}$

(f) Chromium (III) oxide

Ans: $\mathrm{Cr}_{2} \mathrm{O}_{3}$

7. Suggest a list of the substances where carbon can exhibit oxidation states from –4 to +4 and nitrogen from –3 to +5.

Ans:

The substances where nitrogen can exhibit oxidation states from –3 to +5 are listed in the following table.

The oxidation number (O.N.) of $\mathrm{S}$ in sulphur dioxide $\left(\mathrm{SO}_{2}\right)$ is $+4$, while the O.N. of $\mathrm{S}$ can range from $+6$ to $-2$.

As a result, $\mathrm{SO}_{2}$ can function as both an oxidising and a reducing agent.

The O.N. of $\mathrm{O}$ in hydrogen peroxide $\left(\mathrm{H}_{2} \mathrm{O}_{2}\right)$ is $-1$, and the range of $\mathrm{O} . \mathrm{N}$. that $\mathrm{O}$ can have is 0 to $-2$. The oxidation values $+1$ and $+2$ are also possible for $\mathrm{O}$.

As a result, $\mathrm{H}_{2} \mathrm{O}_{2}$ can function as both an oxidizing and a reducing agent.

As a result, in this scenario, the O.N. of $\mathrm{O}$ can only drop. As a result, $\mathrm{O}_{3}$ serves solely as an oxidant.

The O.N. of $\mathrm{N}$ in nitric acid $\left(\mathrm{HNO}_{3}\right)$ is $+5$, and the range of $\mathrm{O} . \mathrm{N}$ that $\mathrm{N}$ can have from $+5$ to $-3$. As a result, in this scenario, the O.N. of $\mathrm{N}$ can only drop. As a result, HNO, serves solely as an oxidant.

9. Consider the reactions:

(a) $6 \mathrm{CO}_{2}(\mathrm{~g})+6 \mathrm{H} 2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}(\mathrm{aq})+6 \mathrm{O}_{2}(\mathrm{~g})$

(b) $\mathrm{O}_{3}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}_{2}(1) \rightarrow \mathrm{H}_{2} \mathrm{O}(1)+2 \mathrm{O}_{2}(\mathrm{~g})$

Why it is more appropriate to write these reactions as:

(a) $6 \mathrm{CO}_{2}(\mathrm{~g})+12 \mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}(\mathrm{aq})+6 \mathrm{H}_{2} \mathrm{O}(1)+6 \mathrm{O} 2(\mathrm{~g})$

Ans: The $\mathrm{H}_{2}$ produced in step 1 reduces $\mathrm{CO}_{2}$, thereby producing glucose $\left(\mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\right)$ and $\mathrm{H}_{2} \mathrm{O}$.

$6 \mathrm{CO}_{2(\mathrm{~g})}+12 \mathrm{H}_{2(\mathrm{~g})} \rightarrow \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6(s)}+6 \mathrm{H}_{2} \mathrm{O}_{(i)}$

Now, the net reaction of the process is given as: $\left.2 \mathrm{H}_{2} \mathrm{O}_{(t)} \rightarrow 2 \mathrm{H}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})}\right] \times 6$

$\dfrac{6 C O_{2(g)}+12 H_{2(g)} \rightarrow C_{6} H_{12} O_{6(s)}+6 H_{2} O_{(l)}}{6 C O_{2(g)}+12 H_{2} O_{(l)} \rightarrow C_{6} H_{12} O_{6(g)}+6 H_{2} O_{(l)}+6 O_{2(g)}}$

It is more appropriate to write the reaction as given above because water molecules are also produced in the process of photosynthesis. The path of this reaction can be investigated by using radioactive $\mathrm{H}_{2} \mathrm{O}_{18}$ in place of $\mathrm{H}_{2} \mathrm{O}$

(b) $\mathrm{O}_{3}(\mathrm{~g})+\mathrm{H}_{2} \mathrm{O}_{2}(\mathrm{l}) \rightarrow \mathrm{H}_{2} \mathrm{O}(1)+\mathrm{O}_{2}(\mathrm{~g})$

Ans: $\mathrm{O}_{2}$ is produced from each of the two reactants $\mathrm{O}_{3}$ and $\mathrm{H}_{2} \mathrm{O}_{2} .$ For this reason, $\mathrm{O}_{2}$ is written twice.

The given reaction involves two steps. First, $\mathrm{O}_{3}$ decomposes to form $\mathrm{O} 2$ and $\mathrm{O}$. In the second step, $\mathrm{H}_{2} \mathrm{O}_{2}$ reacts with the O produced in the first step, thereby producing $\mathrm{H}_{2} \mathrm{O}$ and $\mathrm{O}_{2}$

$O_{3(g)} \rightarrow O_{2(g)}+O_{(g)}$

$\frac{\mathrm{H}_{2} \mathrm{O}_{2(t)}+\mathrm{O}_{(g)} \rightarrow \mathrm{H}_{2} \mathrm{O}_{(t)}+\mathrm{O}_{2(g)}}{2 \mathrm{H}_{2} \mathrm{O}_{2(i)}+\mathrm{O}_{3(g)} \rightarrow \mathrm{H}_{2} \mathrm{O}_{(t)}+\mathrm{O}_{2(g)}+\mathrm{O}_{2(\mathrm{~g})}}$

The path of this reaction can be investigated by using, $\mathrm{H}_{2} \mathrm{O}_{2}^{18}$ or $\mathrm{O}_{3}^{18}$

10. The compound $\mathrm{AgF}_{2}$ is an unstable compound. However, if formed, the compound acts as a very strong oxidizing agent. Why?

Ans:

$\mathrm{Ag}$ in $\mathrm{AgF}_{2}$ has an oxidation state of $+2$. However, $\mathrm{Ag}$ 's oxidation state of $+2$ is unstable.

As a result, silver quickly takes an electron to create $\mathrm{Ag}+$ whenever $\mathrm{AgF}_{2}$ is formed. This helps to reduce $\mathrm{Ag}$ 's oxidation state from $+2$ to $+1$, which is a more stable condition. As a result, $\mathrm{AgF}_{2}$ is an extremely powerful oxidizing agent.

11. Whenever a reaction between an oxidizing agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidizing agent is in excess. Justify this statement giving three illustrations.

Ans:

When an oxidizing agent and a reducing agent react, a lower oxidation state compound is formed if the reducing agent is in excess, and a higher oxidation state compound is formed if the oxidizing agent is in excess. As an example, consider the following:

(i) Reducing and oxidising agents, respectively, are $P_{4}$ and $F_{2}$.

When an excess of $\mathrm{P}_{4}$ is treated with $\mathrm{F}_{2}, \mathrm{PF}_{3}$ is formed, with a positive oxidation number (O.N.) for $\mathrm{P}$.

However, if $P_{4}$ is treated with an excessive amount of $F_{2}, P F_{5}$ is formed, with a P.N. of $+5 .$

(ii) $\mathrm{O}_{2}$ is an oxidising agent, whereas $\mathrm{K}$ is a reducing agent.

$\mathrm{K}_{2} \mathrm{O}$ is generated when an excess of $\mathrm{K}$ reacts with $\mathrm{O}_{2}$, with the O.N. of $\mathrm{O}$ being $-2 .$

$4 \mathrm{~K}(\text { excess })+\mathrm{O}_{2} \rightarrow 2 \mathrm{~K}_{2} \mathrm{O}$

When $K$ reacts with an excess of $\mathrm{O}_{2}$, however, $2 \mathrm{~K}_{2} \mathrm{O}_{2}$ is produced, with the O.N. of $\mathrm{O}$ being -

$4 \mathrm{~K}+\mathrm{O}_{2}(\text { excess }) \rightarrow 2 \mathrm{~K}_{2} \mathrm{O}_{2}$

While $C$ is a reducing agent, $\mathrm{O}_{2}$ is an oxidizing agent.

$\mathrm{CO}$ is created when an excess of $\mathrm{C}$ is burned in the presence of inadequate $\mathrm{O}_{2}$, with the O.N. of $\mathrm{C}$ being $+2$

$\mathrm{C}(\text { excess })+\mathrm{O}_{2} \rightarrow \mathrm{CO}$

If there is an excess of $\mathrm{O}_{2}$ in the combustion of $\mathrm{C}, \mathrm{CO}_{2}$ is generated, with the O.N. of C being $+4$

$\mathrm{C}+\mathrm{O}_{2}(\text { excess }) \rightarrow \mathrm{CO}_{2}$

12. How do you count for the following observations? 

(a) Though alkaline potassium permanganate and acidic potassium permanganate both are used as oxidants, yet in the manufacture of benzoic acid from toluene we use alcoholic potassium permanganate as an oxidant. Why? Write a balanced redox equation for the reaction.

(b) When concentrated sulphuric acid is added to an inorganic mixture containing chloride, we get colorless pungent smelling gas $\mathrm{HCl}$, but if the mixture contains bromide then we get red vapour of bromine. Why?

Ans:  (a) Alcoholic potassium permanganate is utilized as an oxidant in the production of benzoic acid from toluene for the following reasons.

(i) In a neutral medium, OH- ions are produced in the reaction itself. As a result, the cost of adding an acid or a base can be reduced.

(ii) Because both $\mathrm{KMnO}_{4}$ and alcohol are polar, they are homogenous. Because they a both organic molecules, toluene and alcohol are also homogenous.

In a homogeneous medium, reactions can proceed more quickly than in a heterogeneous one. As a result, $\mathrm{KMnO}_{4}$ and toluene might react more quickly in alcohol.

For the reaction in a neutral medium, the balanced redox equation is as follows:

$\mathrm{C}_{6} \mathrm{H}_{5}-\mathrm{CH}_{3}(l)+2 \mathrm{MnO}_{4}^{-}(\text {alcoholic }) \rightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-} \text {(alcoholic) }$

$+2 \mathrm{MnO}_{2}(s)+\mathrm{H}_{2} \mathrm{O}(l)+\mathrm{OH}^{-}(a q)$

When concentrated $\mathrm{H}_{2} \mathrm{SO}_{4}$ is introduced to an inorganic bromide mixture, $\mathrm{HBr}$ is generated at first. With the formation of red bromine vapour, $\mathrm{HBr}$, as a powerful reducing agent, lowers $\mathrm{H}_{2} \mathrm{SO}_{4}$ to $\mathrm{SO}_{2}$.

$\begin{aligned} 2 \mathrm{NaBr}+2 \mathrm{H}_{2} \mathrm{SO}_{4} & \rightarrow 2 \mathrm{NaHSO}_{4}+2 \mathrm{HBr} \\ 2 \mathrm{HBr}+\mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow & \mathrm{Br}_{2}+\mathrm{SO}_{2}+2 \mathrm{H}_{2} \mathrm{O} \\ & \text { (red vapour) } \end{aligned}$

When concentrated $\mathrm{H}_{2} \mathrm{SO}_{4}$ is added to an inorganic combination with chloride, a pungent-smelling gas ( $\mathrm{HCl}^{\prime}$ ) is produced. Because $\mathrm{HCl}$ is a poor reducing agent, it cannot convert $\mathrm{H}_{2} \mathrm{SO}_{4}$ to $\mathrm{SO}_{2}$

$2 \mathrm{NaCl}+2 \mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow 2 \mathrm{NaHSO}_{4}+2 \mathrm{HCl}$

13. Identify the substance oxidized, reduced, oxidizing agent, and reducing agent for each of the following reactions:

(a) $2 \mathrm{AgBr}(\mathrm{s})+\mathrm{C}_{6} \mathrm{H}_{6} \mathrm{O}_{2} \text { (aq) } \rightarrow 2 \mathrm{Ag}(\mathrm{s})+2 \mathrm{HBr}(\mathrm{aq})+\mathrm{C}_{6} \mathrm{H}_{4} \mathrm{O}_{2}(\mathrm{aq})$

Ans: 

$\text { Oxidized substance } \rightarrow \mathrm{C}_{6} \mathrm{H}_{6} \mathrm{O}_{2}$

Reduced substance $\rightarrow \mathrm{AgBr}$

Oxidizing agent $\rightarrow \mathrm{AgBr}$

Reducing agent $\rightarrow \mathrm{C}_{6} \mathrm{H}_{6} \mathrm{O}_{2}$

(b) $\mathrm{HCHO}(1)+2\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}\right]^{+}(\mathrm{aq})+3 \mathrm{OH}^{\circ}(\mathrm{aq}) \rightarrow 2 \mathrm{Ag}(\mathrm{s})+\mathrm{HCOO}^{-}(\mathrm{aq})+4 \mathrm{NH}_{3}(\mathrm{aq})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{I})$

Ans: Oxidized substance $\rightarrow$ HCHO 

Reduced substance $\rightarrow\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}\right]^{+}$ Oxidising agent $\rightarrow\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}\right]^{+}$ Reducing agent $\rightarrow \mathrm{HCH}$ 

(c) $\mathrm{HCHO}(\mathrm{I})+2 \mathrm{Cu}^{2+}(\mathrm{aq})+5 \mathrm{OH}^{\circ}(\mathrm{aq}) \rightarrow \mathrm{Cu}_{2} \mathrm{O}(\mathrm{s})+\mathrm{HCOO}^{\circ}$ (aq) $+3 \mathrm{H}_{2} \mathrm{O}(\mathrm{I})$

Ans: Oxidised substance $\rightarrow$ HCHO

Reduced substance $\rightarrow \mathrm{Cu}^{2+}$

Oxidising agent $\rightarrow \mathrm{Cu}^{2+}$

Reducing agent $\rightarrow$ HGHO

(d) $\mathrm{N}_{2} \mathrm{H}_{4}(\mathrm{I})+2 \mathrm{H}_{2} \mathrm{O}_{2}$ (I) $\rightarrow \mathrm{N}_{2}(\mathrm{~g})+4 \mathrm{H}_{2} \mathrm{O}(\mathrm{I})$

Ans: Oxidised substance $\rightarrow \mathrm{N}_{2} \mathrm{H}_{4}$

Reduced substance $\rightarrow \mathrm{H}_{2} \mathrm{O}_{2}$

Oxidising agent $\rightarrow \mathrm{H}_{2} \mathrm{O}_{2}$

Reducing agent $\rightarrow \mathrm{N}_{2} \mathrm{H}_{4}$

(e) $\mathrm{Pb}(\mathrm{s})+\mathrm{Pb} \mathrm{O}_{2}(\mathrm{~s})+2 \mathrm{H}_{2} \mathrm{SO}_{4}(\mathrm{aq}) \rightarrow 2 \mathrm{PbSO}_{4}(\mathrm{~s})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{I})$

Ans: Oxidised substance $\rightarrow$ Reduced substance $\rightarrow \mathrm{PbO}_{2}$

Oxidising agent $\rightarrow \mathrm{PbO}$

14. Consider the reactions:

$2 \mathrm{~S}_{2} \mathrm{O}_{3}^{2 \cdot}(\mathrm{aq})+\mathrm{I}_{2}(\mathrm{~s}) \rightarrow \mathrm{S}_{4} \mathrm{O}_{6}{ }^{2-}(\mathrm{aq})-2 \mathrm{I}^{-}(\mathrm{aq})$

$\mathrm{S}_{2} \mathrm{O}_{3}{ }^{2-}(\mathrm{aq})+2 \mathrm{Br}_{2}(1)+5$ $\mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \rightarrow 2$ $\mathrm{SO}_{4}^{2-}(\mathrm{aq})+4 \mathrm{Br}^{-}(\mathrm{aq})+10$ $\mathrm{H}^{+}(\mathrm{aq})$

Why does the same reductant, thiosulphate react differently with iodine and bromine?

Ans: $2 \mathrm{~S}_{2} \mathrm{O}_{3}^{2-}(a q)+\mathrm{I}_{2}(s) \longrightarrow \mathrm{S}_{4} \mathrm{O}_{6}^{2-}(a q)+2 \mathrm{I}^{-}(a q)$

$\stackrel{+2-2}{\mathrm{~S}_{2} \mathrm{O}_{3}^{2-}(a q)+2 \mathrm{Br}_{2}(l)+.5 \mathrm{H}_{2} \mathrm{O}(l) \longrightarrow}$

${2 \mathrm{SO}_{4}^{+6-2}(a q)+4 \mathrm{Br}^{-}(a q)+10 \mathrm{H}^{+}(a q)}$

When compared to $\mathrm{I}_{2}$, bromine is a more powerful oxidizer. In $\mathrm{SO}_{4}{ }^{2-}$, it oxidises the $\mathrm{S}$ of $\mathrm{S}_{2} \mathrm{O}_{3}^{2}$ to a higher oxidation state $+6$.

In $\mathrm{S}_{4} \mathrm{O}_{6}{ }^{2-}, \mathrm{I}_{2}$ oxidises S from $\mathrm{S}_{2} \mathrm{O}_{3}{ }^{2}$ to a lower oxidatión state of $2.5 .$ As a result, the same reductant, thiosulphate, reacts with bromine and iodine in distinct ways.

15. Justify giving reactions that among halogens, fluorine is the best oxidant and among hydrohalic compounds, hydroiodic acid is the best reductant.

Ans:  $\mathrm{F}_{2}$ can also oxidize $\mathrm{Cl}$ to $\mathrm{Cl}_{2}, \mathrm{Br}^{-}$to $\mathrm{Br}_{2}$ and $\mathrm{I}^{-}$to $\mathrm{I}_{2}$

$\mathrm{F}_{2(\mathrm{aq})}+2 \mathrm{Cl}_{(s)} \rightarrow 2 \mathrm{~F}_{(\mathrm{aq})}+\mathrm{Cl}_{(\mathrm{g})}$

$\mathrm{P}_{2(\mathrm{aq})}+2 \mathrm{I}_{(\mathrm{aq})} \rightarrow 2 \mathrm{~F}_{(\mathrm{aq})}+\mathrm{I}_{2(\mathrm{~s})}$

$\mathrm{Cl}_{2}, \mathrm{~B} \mathrm{r}_{2}$, and $\mathrm{I}_{2}$, on the other hand, are unable to convert $\mathrm{F}^{-}$to $\mathrm{F}_{2}$. Halogens have an oxidizing power of $\mathrm{I}_{2}<\mathrm{Br}_{2}<\mathrm{Cl}_{2}<\mathrm{F}_{2}$. Fluorine, as a result, is the best halogen oxidant.

$\mathrm{H}_{2} \mathrm{SO}_{4}$ can be converted to $\mathrm{SO}_{2}$ using $\mathrm{HI}$ and $\mathrm{HBr}$, but not with $\mathrm{HCl}$ or $\mathrm{HF}$. HI and $\mathrm{HBr}$ are thus more effective reductants than $\mathrm{HCl}$ and $\mathrm{HF}$

$2 \mathrm{HI}+\mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow \mathrm{I}_{2}+\mathrm{SO}_{2}+2 \mathrm{H}_{2} \mathrm{O}$

$2 \mathrm{HBr}+\mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow \mathrm{Br}_{2}+\mathrm{SO}_{2}+2 \mathrm{H}_{2} \mathrm{O}$

I can reduce $\mathrm{Cu}^{2+}$ to $\mathrm{Cu}^{+}$once more, whereas $\mathrm{Br}^{-}$cannot.

$4 \mathrm{I}_{(\mathrm{aq})}+2 \mathrm{Cu}^{2+}{(a q)} \rightarrow \mathrm{Cu}_{2} \mathrm{I}_{2(\mathrm{f})}+\mathrm{I}_{2(\mathrm{aq})}$

As a result, among hydrohalic compounds, hydroiodic acid is the best reductant.

Hydrohalic acids' reducing power thus grows in the order of $\mathrm{HF}<\mathrm{HCl}<\mathrm{HBr}<\mathrm{HI}$

16. Why does the following reaction occur?

$\mathrm{XeO}_{6}^{4-}(\mathrm{aq})+2 \mathrm{~F}^{-}(\mathrm{aq}) \rightarrow \mathrm{XeO}_{3}(\mathrm{~g})+\mathrm{F}_{2}(\mathrm{~g})+3 \mathrm{H}_{2} \mathrm{O}(\mathrm{l})$

What conclusion about the compound $\mathrm{NaXeO}_{6}$ (of which $\mathrm{XeO}_{6}^{4}$ is a part) can be drawn from the reaction?

Ans: Because $\mathrm{XeO}_{6}^{4-}$ oxidizes $\mathrm{F}^{-}$and $\mathrm{F}^{-}$decreases $\mathrm{XeO}_{6}{ }^{4-}$, the stated reaction occurs.

$\mathrm{XeO}_{6}^{4-}(\mathrm{aq})+2 \mathrm{~F}^{-}(\mathrm{aq}) \rightarrow \mathrm{XeO}_{3}(\mathrm{~g})+\mathrm{F}_{2}(\mathrm{~g})+3 \mathrm{H}_{2} \mathrm{O}(\mathrm{l})$

Xe 's oxidation number (O.N.) falls from $+8$ in $\mathrm{XeO}_{6}^{4}$ to $+6$ in $\mathrm{XeO}_{3}$, while $\mathrm{F}$ 's $\mathrm{O} . \mathrm{N}$. rises from $-1$ in $\mathrm{F}^{-}$to $\mathrm{O}$ in $\mathrm{F}_{2}$

As a result, we can deduce that $\mathrm{NaXeO}_{6}{ }^{4}$ is a more powerful oxidizer than $\mathrm{F}$

17. Consider the reactions:

(a) $\mathrm{H}_{3} \mathrm{PO}_{2}(\mathrm{aq})+4 \mathrm{AgNO}_{3}(\mathrm{aq})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{H}_{3} \mathrm{PO}_{4}(\mathrm{aq})+4 \mathrm{Ag}(\mathrm{s})+4 \mathrm{H} \mathrm{NO}_{3}(\mathrm{aq})$

(b) $\mathrm{H}_{3} \mathrm{PO}_{2}(\mathrm{aq})+2 \mathrm{CuSO}_{4}(\mathrm{aq})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{H}_{3} \mathrm{PO}_{4}(\mathrm{aq})+2 \mathrm{Cu}(\mathrm{s})+\mathrm{H}_{2} \mathrm{SO}_{4}(\mathrm{aq})$

(c) $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{CHO}(\mathrm{l})+2\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}\right]^{+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})+4 \mathrm{NH}_{3}(\mathrm{aq})$

(d) $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{CHO}(\mathrm{l})+2 \mathrm{Cu}^{2+}(\mathrm{aq})+5 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow$ No change observed.

What inference do you draw about the behaviour of $\mathrm{Ag}^{+}$ and $\mathrm{Cu}^{2+}$ from these reactions?

Ans: In reactions (a) and (b), $\mathrm{Ag}^{+}$and $\mathrm{Cu}^{2+}$, respectively, act as oxidizing agents.

Ag+ oxidizes $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{CHO}$ to $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COO}^{-}$in reaction $(\mathrm{c})$, but $\mathrm{Cu}^{2+}$ cannot oxidize $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{CHO}$ in reaction $(\mathrm{d})$

As a result, $\mathrm{Ag}+$ is a more powerful oxidizing agent than $\mathrm{Cu}^{2+}$

18. Balance the following redox reactions by ion-electron method:

(a) $\mathrm{MnO}^{-}(\mathrm{aq})+\mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_{2}(\mathrm{~s})+\mathrm{I}_{2}(\mathrm{~s})$

Ans: Step 1 : The following are the two half reactions involved in the given reaction:

Half-reaction of oxidation $\left.\mathrm{I}_{(\mathrm{a} \phi}\right) \rightarrow \mathrm{I}_{2(\mathrm{~s})}$

Half-reaction of reduction $\mathrm{MnO}_{4}$ (aq) $\rightarrow \mathrm{MnO}_{2(\mathrm{aq})}$

Step 2: We have the following equation for balancing $\mid$ in the oxidation half reaction:

$2 \mathrm{~F}_{(\mathrm{aq})} \rightarrow \mathrm{I}_{2(\mathrm{~s})}$

To balance the charge, we add $2 \mathrm{e}^{-}$to the reaction's RHS.

$2 \mathrm{I}_{(\mathrm{aq})}^{-} \rightarrow \mathrm{I}_{2(\mathrm{~s})}+2 \mathrm{e}^{-}$

Step 3: Mn 's oxidation state has decreased from+7 to+4 throughout the reduction half reaction.

$\mathrm{MnO}_{4}^{-}+3 \mathrm{e}^{-} \rightarrow \mathrm{MnO}_{2(\mathrm{aq})}$

Step 4: Six O atoms are on the RHS and four $\mathrm{O}$ atoms are on the LHS in this equation. As a result, the LHS is given two water molecules.

$\mathrm{MnO}_{4(\mathrm{aq})}^{-}+2 \mathrm{H}_{2} \mathrm{O}+3 \mathrm{e}^{-} \rightarrow \mathrm{MnO}_{2(\mathrm{aq})}+4 \mathrm{OH}^{-}$

Step 5: By multiplying the oxidation half reaction by 3 and the reduction half reaction by 2 , we may equalize the quantity of electrons.

$6 \mathrm{I}_{(\mathrm{aq})}^{-} \rightarrow 3 \mathrm{I}_{2(\mathrm{~s})}+6 \mathrm{e}^{-}$

${2 \mathrm{MnO}_{4}{ }^{-}(\mathrm{aq})}+4 \mathrm{H}_{2} \mathrm{O}+6 \mathrm{e}^{-} \rightarrow 2 \mathrm{MnO}_{2(\mathrm{aq})}+8 \mathrm{OH}_{(a q)}^{-}$

Step 6: When the two half reactions are added together, we get the net balanced redox reaction:

$6 \mathrm{I}_{(\mathrm{aq})}^{-}+2 \mathrm{MnO}_{4}{ }_{(\mathrm{aq})}+4 \mathrm{H}_{2} \mathrm{O} \rightarrow 2 \mathrm{MnO}_{2(\mathrm{aq})}+8 \mathrm{OH}_{(a q)}^{-}$

(b) $\mathrm{MnO}^{-}(\mathrm{aq})+\mathrm{SO}_{2}(\mathrm{aq}) \rightarrow \mathrm{Mn}^{2+}(\mathrm{aq})+\mathrm{HSO}_{4}^{-}(\mathrm{aq})$

Ans: If we repeat the processes from part (a), we get the following oxidation half reaction:

$\mathrm{SO}_{2(\mathrm{~g})}+2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \rightarrow \mathrm{HSO}_{4}{ }^{-}(\mathrm{aq})+3 \mathrm{H}^{+}{ }_{(\mathrm{aq})}$

And the half-reduction reaction is as follows:

We get the net balanced redox reaction by multiplying the oxidation half reaction by 5 and the reduction half reaction by 2 , then adding them.

(c) $\mathrm{H}_{2} \mathrm{O}_{2}(\mathrm{aq})+\mathrm{Fe}^{2+}(\mathrm{a} q) \rightarrow \mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{H}_{2} \mathrm{O}(\mathrm{l})$

Ans: Using the same techniques as in part $(a)$, we get the following oxidation half reaction:

$\mathrm{Fe}^{2+}{ }_{(\mathrm{aq})} \rightarrow \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})}+\mathrm{e}^{-}$

And the half-reduction reaction is as follows:

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+2 \mathrm{H}_{(\mathrm{aq})}^{+}+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}$

We get the net balanced redox reaction by multiplying the oxidation half reaction by 2 and then adding it to the reduction half reaction:

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+2 \mathrm{Fe}_{(\mathrm{aq})}^{2+}+2 \mathrm{H}^{+}{ }_{(\mathrm{ac})} \rightarrow 2 \mathrm{Fe}_{(2 q)}{ }^{3+}+2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}$

(d) $\mathrm{Cr}_{2} \mathrm{O}_{7}{ }^{2-}+\mathrm{SO}_{2}(\mathrm{~g}) \rightarrow \mathrm{Cr}^{3+}(\mathrm{aq})+\mathrm{SO}_{4}{ }^{2-}(\mathrm{aq})$

Ans: Using the same techniques as in part (a), we get the following oxidation half reaction:

$\mathrm{SO}_{2(\mathrm{~g})}+2 \mathrm{H}_{2} \mathrm{O}_{(1)} \rightarrow \mathrm{SO}^{2}_{4(2 q)}+4 \mathrm{H}_{(\mathrm{aq})}^{+}+2 \mathrm{e}^{-}$

And the half-reduction reaction is as follows:

$\mathrm{Cr}_{2} \mathrm{O}_{7(\mathrm{aq})}^{2-}+14 \mathrm{H}_{(a q)}^{+}+6 \mathrm{e}^{-} \rightarrow \mathrm{Cr}^{3+}{ }_{(\mathrm{aq})}+7 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}$

We get the net balanced redox reaction by multiplying the oxidation half reaction by 3 and then adding it to the reduction half reaction:

$\mathrm{Cr}_{2} \mathrm{O}^{2 \cdot}{ }_{7(\mathrm{aq})}+3 \mathrm{SO}_{2(\mathrm{~g})}+2 \mathrm{H}_{(\mathrm{aq})}^{+} \rightarrow 2 \mathrm{Cr}^{3+}{ }_{\left(\mathrm{a}_{9}\right)}+3 \mathrm{SO}^{2-}{ }_{4(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}$

19. Balance the following equations in basic medium by ion-electron method and oxidation number methods and identify the oxidizing agent and the reducing agent.

$\mathrm{P}_{4(s)}+\mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow \mathrm{PH}_{3 \mathrm{g}}+\mathrm{HPO}_{2(\mathrm{aq})}^{-}$

Ans: (a) The oxidation number of $P$ drops from 0 to $-3$ in $P_{4}$ and increases from 0 to $+2$ in $\mathrm{HPO}_{2} .$ As a result, $\mathrm{P}_{4}$ serves as both an oxidizing and reducing agent in this process. Ion-electron method:

The half-equation for oxidation is:

$\mathrm{P}_{4(\mathrm{~s})} \rightarrow \mathrm{HPO}_{2(a q)}^{-}$

The $P$ atom is balanced in the following way:

$\mathrm{P}_{4(\mathrm{~s})}^{0} \rightarrow 4 \mathrm{HPO}_{2(a q)}^{-}$

The O.N. is balanced by adding eight electrons in the following way:

$\mathrm{P}_{4(\mathrm{~s})} \rightarrow 4 \mathrm{HPO}_{2(a)}+8 \mathrm{e}^{-}$

The charge is balanced by the addition of $12 \mathrm{OH}^{-}$ as follows:

$\mathrm{P}_{4(\mathrm{~s})}+12 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow 4 \mathrm{HPO}_{2(a q)}^{-}+8 \mathrm{e}^{-}$

By adding $4 \mathrm{H}_{2} \mathrm{O}$, the $\mathrm{H}$ and $\mathrm{O}$ atoms are balanced.

$\mathrm{P}_{4(s)}+12 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow 4 \mathrm{HPO}_{2(a q)}^{-}+4 \mathrm{H}_{2} \mathrm{O}_{(1)}+8 \mathrm{e}^{-} \ldots . .(\mathrm{i})$

The half-reduction equation is as follows:

$\mathrm{P}_{4(\mathrm{~s})}+\mathrm{PH}_{3(\mathrm{~g})}$

The $\mathrm{P}$ atom is in a state of equilibrium.

By adding 12 electrons to the $Q . N$., it is balanced:

$\mathrm{P}_{4(\mathrm{~s})}+12 \mathrm{e}^{-} \rightarrow 4 \mathrm{PH}_{3(\mathrm{~g})}$

The charge is balanced by the addition of $12 \mathrm{OH}^{-}$as follows:

$\mathrm{P}_{4(\mathrm{~s})}+12 \mathrm{e}^{-} \rightarrow 4 \mathrm{PH}_{3(\mathrm{~g})}+12 \mathrm{OH}_{(\mathrm{aq})}^{-}$

$12 \mathrm{H}_{2} \mathrm{O}$ is used to balance the 0 and $\mathrm{H}$ atoms as follows:

$\mathrm{P}_{4(s)}+12 \mathrm{H}_{3} \mathrm{O}_{(1)}+12 \mathrm{e}^{-} \rightarrow 4 \mathrm{PH}_{3(\mathrm{~g})}+12 \mathrm{OH}_{(2 q)}^{-} \quad \text { (ii) }$

The balanced chemical equation can be found by multiplying equations $\mid$ and (ii) by 3 and then adding them.

$5 \mathrm{P}_{4(\mathrm{~s})}+12 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}+12 \mathrm{HO}_{(\mathrm{aq})}^{-} \rightarrow 8 \mathrm{PH}_{3(\mathrm{~g})}+12 \mathrm{HPO}_{(\mathrm{aq})}^{-}$

(b) $\mathrm{N}_{2} \mathrm{H}_{4}(\mathrm{l})+\mathrm{ClO}_{3}^{-}(\mathrm{aq}) \rightarrow \mathrm{NO}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g})$

Ans:

$\mathrm{N}^{\prime}$ s oxidation number rises from $-2$ in $\mathrm{N}_{2} \mathrm{H}_{4}$ to $+2$ in $\mathrm{NO}$, while $\mathrm{Cl}$ 's oxidation number falls from $+5$ in $\mathrm{ClO}_{3}$ to $-1$ in $\mathrm{Cl}^{-} .$As a result, $\mathrm{N}_{2} \mathrm{H}_{4}$ is the reducing agent and $\mathrm{ClO}_{3}$ is the oxidizing agent in this reaction.

Ion-electron method:

The half-equation for oxidation is:

$-2$

$\mathrm{~N}_{2} \mathrm{H}_{4(1)} \rightarrow \mathrm{NO}_{(\mathrm{g})}$

The $N$ atoms are balanced in the following way:

$\mathrm{N}_{2} \mathrm{H}_{4(1)} \rightarrow 2 \mathrm{NO}_{(\mathrm{g})}$

By adding 8 electrons to the oxidation number, the oxidation number is balanced:

$\mathrm{N}_{2} \mathrm{H}_{4(\mathrm{l})} \rightarrow 2 \mathrm{NO}_{\mathrm{fg})}+8 \mathrm{e}^{-}$

$8 \mathrm{OH}^{-}$ions are added to balance the charge as follows:

$\mathrm{N}_{2} \mathrm{H}_{4(\mathrm{I})}+8 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow 2 \mathrm{NO}_{(\mathrm{g})}+8 \mathrm{e}^{-}$

$6 \mathrm{H}_{2} \mathrm{O}$ is added to balance the $\mathrm{O}$ atoms as follows:

$\mathrm{N}_{2} \mathrm{H}_{4(1)}+8 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow 2 \mathrm{NO}_{(\mathrm{g})}+6 \mathrm{H}_{2} \mathrm{O}+8 \mathrm{e}^{-} \ldots .$

The half-reduction equation is as follows:

$\stackrel{+5}{\mathrm{Cl} \mathrm{O}^{-}}_{3(\mathrm{aq})}^{-1} \rightarrow \mathrm{Cl}_{(\mathrm{aq})}^{-}$

By adding 6 electrons to the oxidation number, the oxidation number is balanced:

$\mathrm{ClO}_{3(\mathrm{aq})}+6 \mathrm{e}^{-} \rightarrow \mathrm{Cl}_{(\mathrm{aq})}^{-}$

$6 \mathrm{OH}^{-}$ions are added to balance the charge as follows:

$\mathrm{ClO}_{3(a q)}^{-}+6 \mathrm{e}^{-} \rightarrow \mathrm{Cl}_{(a q)}^{-}+6 \mathrm{OH}_{(\mathrm{aq})}^{-}$

By adding $3 \mathrm{H}_{2} \mathrm{O}$ as follows, the O atoms are balanced.

Equation I is multiplied by 3 and equation (ii) is multiplied by 4, resulting in the balanced equation:

$3 \mathrm{~N}_{2} \mathrm{H}_{4(1)} \rightarrow 6 \mathrm{NO}_{(\mathrm{g})}+4 \mathrm{Cl}_{(\mathrm{aq})}^{-}+6 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}$

Oxidation number method:

Total reduction in $N$ oxidation number

$\mathrm{N}=2 \times 4=8$

Total reduction in $\mathrm{Cl}$ oxidation number

$\mathrm{Cl}=1 \times 6=6$

To balance the rise and decrease in O.N., multiply $\mathrm{N}_{2} \mathrm{H}_{4}$ by three and $\mathrm{ClO}_{3}$ by four.

$3 \mathrm{~N}_{2} \mathrm{H}_{4(\mathrm{l})} \rightarrow 4 \mathrm{ClO}_{3(\mathrm{aq})}^{-} \rightarrow \mathrm{NO}_{(\mathrm{g})}+\mathrm{Cl}_{(\mathrm{aq})}^{-}$

The atoms of $\mathrm{N}$ and $\mathrm{Cl}$ are balanced as follows:

$3 \mathrm{~N}_{2} \mathrm{H}_{4(1)} \rightarrow 4 \mathrm{ClO}_{3(\mathrm{aq})}^{-} \rightarrow 6 \mathrm{NO}_{(\mathrm{g})}+4 \mathrm{Cl}_{(\mathrm{aq})}^{\circ}$

$6 \mathrm{H}_{2} \mathrm{O}$ is added to balance the $\mathrm{O}$ atoms as follows:

$3 \mathrm{~N}_{2} \mathrm{H}_{4(1)} \rightarrow 4 \mathrm{ClO}_{3(\mathrm{aq})} \rightarrow 6 \mathrm{NO}_{(\mathrm{g})}+4 \mathrm{Cl}_{(\mathrm{aq})}^{-}+6 \mathrm{H}_{2} \mathrm{O}$

This is the equation that must be balanced.

(c) $\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{2(\alpha q)} \longrightarrow \mathrm{ClO}_{2(\alpha q)}^{-}+\mathrm{O}_{2(g)}+\mathrm{H}_{(c)}^{+}$

Ans: The oxidation number of $\mathrm{Cl}$ decreases from $+7$ in $\mathrm{Cl}_{2} \mathrm{O}_{7}$ to $+3$ in $\mathrm{ClO}_{2}$ and the oxidation number of $\mathrm{O}$ increases from $-1$ in $\mathrm{H}_{2} \mathrm{O}_{2}$ to zero in $\mathrm{O}_{2}$. Hence, in this reaction, $\mathrm{Cl}_{2} \mathrm{O}_{7}$ is the oxidizing agent and $\mathrm{H}_{2} \mathrm{O}_{2}$ is the reducing agent. Ion-electron method:

The half-equation for oxidation is:

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})} \rightarrow \mathrm{O}_{2(\mathrm{~g})}^{0}$

By adding two electrons to the oxidation number, the oxidation number is balanced as follows:

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})} \rightarrow \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{e}^{-}$

$2 \mathrm{OH}$ - ions are added to balance the charge as follows:

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+2 \mathrm{OH}_{2(\mathrm{~g})}^{-} \rightarrow \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{e}^{-}$

By adding $2 \mathrm{H}_{2} \mathrm{O}_{2}$ as follows, the oxygen atoms are balanced.

$\mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+2 \mathrm{OH}_{2(\mathrm{~g})}^{-} \rightarrow \mathrm{O}_{2(\mathrm{~g})}+2 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{t})}+2 \mathrm{e}^{-} \ldots .(\mathrm{i})$

The half-reduction equation is as follows:

The $\mathrm{Cl}$ atoms are balanced in the following way:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})} \rightarrow \mathrm{ClO}_{2(\mathrm{aq})}^{-}$

By adding 8 electrons to the oxidation number, the oxidation number is balanced:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+8 \mathrm{e}^{-} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}$

6OH' is added to balance the charge as follows:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+8 \mathrm{e}^{-} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}+6 \mathrm{OH}^{-}{ }_{(\mathrm{aq})}$

By adding $3 \mathrm{H}_{2} \mathrm{O}$ as follows, the oxygen atoms are balanced.

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+3 \mathrm{H}_{2} \mathrm{O}+8 \mathrm{e}^{-} \rightarrow 2 \mathrm{ClO}_{2(a q)}^{-}+6 \mathrm{OH}_{(\mathrm{aq})}^{-} \ldots . \text { (ii) }$

By multiplying equation (i) by 4 and adding equation (ii) toit, you can get the balanced equation.

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+4 \mathrm{H}_{2} \mathrm{O}_{2(a q)}+2 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}+4 \mathrm{O}_{2(\mathrm{~g})}+5 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{c})}$

Method for calculating the oxidation number:

The total number of oxidations has decreased $\mathrm{Cl}_{2} \mathrm{O}_{7}=4 \times 2=8$

The total number of oxidations has decreased $\mathrm{H}_{2} \mathrm{O}_{2}=2 \times 1=2$

To balance the rise and decrease in the oxidation number, multiply $\mathrm{H}_{2} \mathrm{O}_{2}$ and $\mathrm{O}_{2}$ by $4 .$

$\mathrm{Cl}_{2} \mathrm{O}_{7 \mathrm{Vg}}+4 \mathrm{H}_{2} \mathrm{O}_{2(a q)} \rightarrow \mathrm{ClO}_{2(\mathrm{aq})}^{-}+4 \mathrm{O}_{2(\mathrm{~g})}$

The $\mathrm{Cl}$ atoms are balanced in the following way:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+4 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}+4 \mathrm{O}_{2(\mathrm{~g})}$

The O atoms are balanced by adding $3 \mathrm{H}_{2} \mathrm{O}$ in the following way:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+4 \mathrm{H}_{2} \mathrm{O}_{2(\text { aq })} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}+4 \mathrm{O}_{2 \mathrm{~g} \mathrm{e}}+3 \mathrm{H}_{2} \mathrm{O}_{41}$

$2 \mathrm{OH}^{-}$and $2 \mathrm{H}_{2} \mathrm{O}$ are used to balance the $\mathrm{H}$ atoms as follows:

$\mathrm{Cl}_{2} \mathrm{O}_{7(\mathrm{~g})}+4 \mathrm{H}_{2} \mathrm{O}_{2(\mathrm{aq})}+2 \mathrm{OH}^{-} \rightarrow 2 \mathrm{ClO}_{2(\mathrm{aq})}^{-}+4 \mathrm{O}_{2(\mathrm{~g})}+5 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}$

This is the equation that must be balanced.

20. What sorts of information can you draw from the following reaction?

$(\mathrm{CN})_{2(\mathrm{~g})}+2 \mathrm{OH}_{(a \mathrm{a})}^{-} \rightarrow \mathrm{CN}_{(2 \mathrm{aq})}^{-}+\mathrm{CNO}_{(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}$

Ans: The carbon oxidation numbers in $(\mathrm{CN})_{2}, \mathrm{CN}^{-}, \mathrm{CNO}^{-}$are $+3,+2$ and +4respectively.

These can be found as follows:

Let $x$ be $C$ 's oxidation number.

$(\mathrm{CN})_{2}$

$2(x-3)=0$

$\therefore x=3$

$\mathrm{CN}^{\circ}$

$x-3=-1$

$\therefore x=2$

$\mathrm{CNO}^{-}$

$x-3-2=-1$

$\therefore x=4$

The carbon oxidation number in various species is:

$[\mathrm{CN}]_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq})}^{-} \rightarrow \mathrm{CN}_{(\text {aq })}^{*}+\mathrm{CNO}_{(\mathrm{aq})}^{-}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{b})}$

In the preceding equation, the same chemical is being reduced and oxidized at the same time. Disproportionation reactions are those in which the same chemical is reduced and oxidized at the same time. As a result, the alkaline breakdown of cyanogen can be considered a disproportionation process.

21. The $\mathrm{Mn}^{3+}$ ion is unstable in solution and undergoes disproportionation to give $\mathrm{Mn}^{2+}, \mathrm{MnO}_{2}$, and $\mathrm{H}+$ ion. Write a balanced ionic equation for the reaction.

Ans: The following is a representation of the provided reaction:

$\mathrm{Mn}^{3+}{ }_{(\mathrm{aq})} \rightarrow \mathrm{Mn}^{2+}{ }_{(\mathrm{aq})}+\mathrm{MnO}_{2(\mathrm{~s})}+\mathrm{H}_{(\mathrm{aq})}^{+}$

The half-equation for oxidation is:

$\stackrel{+3}{\mathrm{Mn}^{3+}}_{(\mathrm{aq})} \rightarrow+\mathrm{MnO}_{2(\mathrm{~s})}^{+4}$

By adding one electron to the oxidation number, the oxidation number is balanced as follows:

$\mathrm{Mn}^{3+}{ }_{(\text {aq })} \rightarrow+\mathrm{MnO}_{2(\mathrm{~s})}+\mathrm{e}^{-}$

The charge is balanced by introducing $4 \mathrm{H}^{+}$ions in the following way:

$\mathrm{Mn}^{3+}{ }_{(\mathrm{aq})} \rightarrow+\mathrm{MnO}_{2(\mathrm{~s})}+4 \mathrm{H}^{+}+\mathrm{e}$

$2 \mathrm{H}_{2} \mathrm{O}$ molecules are added to balance the $\mathrm{O}$ atoms and $\mathrm{H}^{+}$ions as follows:

$\mathrm{Mn}^{3+}_{(a q)}+2 \mathrm{H}_{2} \mathrm{O} \rightarrow+\mathrm{MnO}_{2(s)}+4 \mathrm{H}^{+}+\mathrm{e}^{-} \ldots . .(\mathrm{i})$

The hąlf-reduction equation is as follows:

$\mathrm{Mn}^{3+}{ }_{(\mathrm{aq})} \rightarrow \mathrm{Mn}^{2+}{ }_{(\mathrm{aq})}$

By adding one electron to the oxidation number, the oxidation number is balanced:

$\mathrm{Mn}^{3+}{ }_{(\mathrm{aq})}+\mathrm{e}^{-} \rightarrow \mathrm{Mn}^{2+}{ }_{(\mathrm{aq})}$

Combining equations I and (ii) yields the balanced chemical equation:

$\mathrm{Mn}^{3+}{ }_{(\mathrm{aq})}+2 \mathrm{H}_{2} \mathrm{O} \rightarrow+\mathrm{MnO}_{2(\mathrm{~s})}+2 \mathrm{Mn}^{2+}{(\mathrm{aq})}+4 \mathrm{H}^{+}$

22.Consider the elements:

$\mathrm{Cs}, \mathrm{Ne}, \mathrm{I}$ and $\mathrm{F}$

(a) Identify the element that exhibits only negative oxidation state.

Ans: $F$ has just a $-1$ negative oxidation state.

(b) Identify the element that exhibits only positive oxidation state.

Ans: $\mathrm{Cs}$ has a positive oxidation state of $+1$

(c) Identify the element that exhibits both positive and negative oxidation states.

Ans: Both positive and negative oxidation states are present in my body. It has the following oxidation states: $-1,+1,+3,+5$, and $+7$

(d) Identify the element which exhibits neither the negative nor does the positive oxidation state.

Ans: Ne has a zero-oxidation state. It doesn't have any oxidation states, either negative or positive.

23. Chlorine is used to purify drinking water. Excess of chlorine is harmful. The excess of chlorine is removed by treating with Sulphur dioxide. Present a balanced equation for this redox change taking place in water.

Ans:

The following is a representation of the provided redox reaction:

$\mathrm{Cl}_{2(\mathrm{~s})}+\mathrm{SO}_{2(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{Cl}_{(\mathrm{aq})}^{-}+\mathrm{SO}^{2-}{ }_{4(\mathrm{aq})}$

The half-reaction of oxidation is:

$+4$

$\mathrm{SO}_{2(\mathrm{aq})} \rightarrow \mathrm{SO}^{2-}$

$4(\mathrm{aq})$

By adding two electrons to the oxidation number, the oxidation number is balanced:

$\mathrm{SO}_{2(\mathrm{aq})} \rightarrow \mathrm{SO}^{2-}{ }_{4(\mathrm{aq})}+2 \mathrm{e}^{-}$

The charge is balanced by introducing $4 \mathrm{H}^{+}$ions in the following way:

$\mathrm{SO}_{2(a q)} \rightarrow \mathrm{SO}^{2-}{ }_{4(a q)}+4 \mathrm{H}^{+}+2 \mathrm{e}^{-}$

$2 \mathrm{H}_{2} \mathrm{O}$ molecules are added to balance the $\mathrm{O}$ atoms and $\mathrm{H}+$ ions as follows: The charge is balanced by introducing $4 \mathrm{H}^{+}$ions in the following way:

$\mathrm{SO}_{2(\mathrm{aq})}+2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \rightarrow \mathrm{SO}^{2-}{ }_{4(a q)}+4 \mathrm{H}^{+}+2 \mathrm{e}^{-}$

The half-reduction reaction is as follows:

$\mathrm{Cl}_{2(\mathrm{~s})} \rightarrow \mathrm{Cl}_{(\mathrm{aq})}^{-}$

The chlorine atoms are balanced in the following way:

${ }_{0}^{-1}\mathrm{Cl}_{2(\mathrm{~s})} \rightarrow \mathrm{Cl}^{-}(\mathrm{aq})$

By adding electrons, the oxidation number is restored.

$\mathrm{Cl}_{2(s)}+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{Cl}_{(\mathrm{aq})}^{-\ldots} \ldots \text { (ii) }$

Combining equations I and (ii) yields the balanced chemical equation:

$\mathrm{Cl}_{2(\mathrm{~s})}+2 \mathrm{SO}_{2(\mathrm{aq})}+2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})} \rightarrow 2 \mathrm{Cl}_{(\mathrm{aq})}^{-}+\mathrm{SO}^{2-}{ }_{4(\mathrm{aq})}+4 \mathrm{H}^{+}{ }_{(\mathrm{aq})}$

24. Refer to the periodic table given in your book and now Ans: the following questions: 

(a) Select the possible non-metals that can show disproportionation reaction. 

Ans: One of the reacting compounds must always contain an element that can exist in at least three oxidation states in disproportionation reactions.

(a) Because these elements can exist in three or more oxidation states, disproportionation reactions can occur.

(b) Select three metals that can show a disproportionation reaction.

Ans: Because these elements can exist in three or more oxidation states, disproportionation reactions can occur.

25.In Ostwald’s process for the manufacture of nitric acid, the first step involves the oxidation of ammonia gas by oxygen gas to give nitric oxide gas and steam. What is the maximum weight of nitric oxide that can be obtained starting only with 10.00 g. of ammonia and 20.00 g of oxygen?

Ans: For the above reaction, the balanced chemical equation is:

$4 \mathrm{NH}_{3(\mathrm{~g})}+5 \mathrm{O}_{2(\mathrm{~g})} \rightarrow 4 \mathrm{NO}_{(\mathrm{g})}+6 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}$

$4 \times 17 \mathrm{~g} \quad 5 \times 32 \mathrm{~g} \quad 4 \times 30 \mathrm{~g} \quad 6 \times 18 \mathrm{~g}$

$=68 \mathrm{~g}\quad =160 \mathrm{~g} \quad=120 \mathrm{~g} \quad=108 \mathrm{~g}$

Therefore, $68 \mathrm{~g}$ of $\mathrm{NH}_{3}$ reacts with $160 \mathrm{~g}$ of $\mathrm{O}_{2}$

Thus, $10 \mathrm{~g}$ of $\mathrm{NH}_{3}$ reacts with

$\dfrac{160 \times 10}{68} \mathrm{~g} \text { of } \mathrm{O}_{2}$

$23.53 \mathrm{~g} \text { of } \mathrm{O}_{2}$

However, there is only $20 \mathrm{~g}$ of oxygen accessible.

As a result, $\mathrm{O}_{2}$ is the reaction limiting reagent (we used the amount of $\mathrm{O} 2$ to compute the weight of nitric oxide produced).

Hence, $160 \mathrm{~g}$ of $\mathrm{O}_{2}$ gives $120 \mathrm{~g}$ of NO

$20 \mathrm{~g}$ of $\mathrm{O}_{2}$ gives $\dfrac{120 \times 20}{160} \mathrm{~g}$ of $\mathrm{N}$

Thus, $15 \mathrm{~g}$ of NO

As a result, you can get up to $15 \mathrm{~g}$ of nitric oxide.

26.Using the standard electrode potentials given in the Table 8.1, predict if the reaction between the following is feasible:

(a) $\mathrm{Fe}^{3}(\mathrm{aq})$ and $\mathrm{I}^{-}(\mathrm{aq})$

Ans: The reaction between $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{I}^{-}(\mathrm{aq})$ can be expressed as,

$2 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+2 \mathrm{I}^{-} \rightarrow 2 \mathrm{Fe}^{2+}{ }_{(\mathrm{aq})}+\mathrm{I}_{2(\mathrm{~s})}$

Half-equation for oxidation: $2 \mathrm{I}^{-} \rightarrow+\mathrm{I}_{2(\mathrm{~s})}+2 \mathrm{e}^{-} ; \mathrm{E}^{0}=-0.54 \mathrm{~V}$ Half-equation of reduction

$\dfrac{\left[\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{e}^{-} \rightarrow \mathrm{Fe}^{2+}_{(\mathrm{aq})}\right] \times 2 ; \mathrm{E}^{0}=+0.77 \mathrm{~V}}{2 \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})}+2 \mathrm{I}^{\circ} \rightarrow 2 \mathrm{Fe}^{2+}{ }_{(\mathrm{aq})}+\mathrm{I}_{2(\mathrm{~s})} ; \mathrm{E}^{0}=+0.23 \mathrm{~V}}$

The overall reaction has an $\mathrm{E}^{0}$ of favourable. As a result, the reaction of $\mathrm{Fe}^{3+}$ and $\mathrm{I}_{(\mathrm{aq})}^{-}$ is possible.

(b) $\mathrm{Ag}^{+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$

Ans: The reaction between $\mathrm{Ag}^{+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$ can be described as follows:

$2 \mathrm{Ag}_{(\mathrm{aq})}^{+}+\mathrm{Cu}_{(\mathrm{s})} \rightarrow 2 \mathrm{Ag}_{(\mathrm{s})}+\mathrm{Cu}^{2+}$

Half-equation for oxidation: $\mathrm{Cu}_{(\mathrm{s})} \rightarrow \mathrm{Cu}^{2+}_{\text {(a) }}+2 \mathrm{e}^{-} ; \mathrm{E}^{0}=-0.34 \mathrm{~V}$

Half-equation of reduction

$\dfrac{\left[\mathrm{Ag}^{+}(\mathrm{aq}) \rightarrow \mathrm{e}^{-} \mathbb{} \mathbb{A g}_{(s)}\right] \times 2 ; \mathrm{E}^{0}=+0.80 \mathrm{~V}}{2 \mathrm{Ag}^{+}{ }_{(\mathrm{aq})}+\mathrm{Cu}_{(s)} \rightarrow 2 \mathrm{Ag}_{(s)}+\mathrm{Cu}^{2+} ; \mathrm{E}^{0}=+0.46 \mathrm{~V}}$

The overall reaction has an $\mathrm{E}^{0}$ of favourable. As a result, the reaction of $\mathrm{Ag}^{+}$(aq) and $\mathrm{Cu}(\mathrm{s})$ is possible.

(c) $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$

Ans: The reaction between $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$ can be described as follows:

$2 \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})}+\mathrm{C} \mathrm{a}_{\mathrm{V}} \rightarrow \mathrm{Fe}^{2+}{ }_{(s)}+\mathrm{Cu}^{2+}{ }_{(2 q)}$

Half-equation for oxidation: $\mathrm{Cu}_{(s)} \rightarrow \mathrm{Cu}^{2+}{ }_{\text {(aq) }}+2 \mathrm{e}^{-} ; \mathrm{E}^{0}=-0.34 \mathrm{~V}$

Half-equation of reduction

$\dfrac{\left[\mathrm{Fe}^{3+}{ }_{(\mathrm{aq})}+\mathrm{e}^{-} \rightarrow \mathrm{Fe}^{2+}{ }_{(s)}\right] \times 2 ; \mathrm{E}^{0}=+0.77 \mathrm{~V}}{2 \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})}+\mathrm{Cu}_{(\mathrm{s})} \rightarrow \mathrm{Fe}^{2+}{ }_{(\mathrm{s})}+\mathrm{Cu}^{2+}{ }_{(\mathrm{aq})} ; \mathrm{E}^{0}=+0.43 \mathrm{~V}}$

The overall reaction has an $\mathrm{E}^{0}$ is favourable. As a result, the reaction of $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$ is possible.

(d) $\mathrm{Ag}(\mathrm{s})$ and $\mathrm{Fe}^{3+}(\mathrm{aq})$

Ans: The reaction between $\mathrm{Ag}(\mathrm{s})$ and $\mathrm{Fe}^{3+}(\mathrm{aq})$ can be described as follows:

$\mathrm{Ag}_{(\mathrm{s})}+2 \mathrm{Fe}_{(\mathrm{aq})} \rightarrow \mathrm{Ag}^{+}{ }_{(\mathrm{aq})}+\mathrm{Fe}^{2+}{ }_{(\mathrm{aq})}$

Half-equation for oxidation: $\mathrm{Ag}_{(\mathrm{s})}+\rightarrow \mathrm{Ag}_{(\text {aq })}^{+}+\mathrm{e}^{-} ; \mathrm{E}^{0}=-0.80 \mathrm{~V}$

Half-equation of reduction

$\dfrac{\left[\mathrm{Fe}^{3+}_{(\mathrm{aq})}+\mathrm{e}^{-} \rightarrow \mathrm{Fe}^{2+}{ }_{(\mathrm{s})}\right] \times 2 ; \mathrm{E}^{0}=+0.77 \mathrm{~V}}{\mathrm{Ag}_{(s)}+2 \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})} \rightarrow \mathrm{Ag}^{+}{ }_{(\mathrm{aq})}+\mathrm{Fe}^{2+}{ }_{(\mathrm{aq})} ; \mathrm{E}^{0}=-0.03 \mathrm{~V}}$

The overall reaction has an $\mathrm{E}^{0}$ is not favourable. As a result, the reaction of $\mathrm{Ag}(\mathrm{s})$ and $\mathrm{Fe}^{3+}(\mathrm{aq})$ is not possible.

(e) $\mathrm{Br}_{2(\mathrm{aq})}$ and $\mathrm{Fe}^{2+}(\mathrm{aq})$

Ans: The reaction between $\mathrm{Br}_{2(\mathrm{aq})}$ and $\mathrm{Fe}^{2+}($ aq $)$ can be described as follows

Half-equation for oxidation: $\mathrm{Br}_{2(\mathrm{~s})}+2 \mathrm{Fe}^{2+}{ }_{(\mathrm{aq})} \rightarrow 2 \mathrm{Br}_{(\mathrm{aq})}^{-}+2 \mathrm{Fe}^{+3}{ }_{(\mathrm{aq})}$

Half-equation of reduction: $\left[\mathrm{Fe}^{2+}{ }_{(\mathrm{aq})} \rightarrow \mathrm{Fe}^{+3}{(\mathrm{aq})}+\mathrm{e}^{-}\right] \times 2 ; \mathrm{E}^{0}=-0.77 \mathrm{~V}$

Half-equation of reduction

$\dfrac{\mathrm{Br}_{2(\mathrm{aq})}+2 \mathrm{e}^{-} \rightarrow \mathrm{Br}_{(\mathrm{aq})}^{-} ; \mathrm{E}^{0}=+1.09 \mathrm{~V}}{\mathrm{Br}_{2(\mathrm{aq})}+2 \mathrm{Fe}^{2+}{ }_{(\mathrm{aq})} \rightarrow 2 \mathrm{Br}_{(\mathrm{aq})}^{-}+2 \mathrm{Fe}^{3+}{ }_{(\mathrm{aq})} ; \mathrm{E}^{0}=+0.32 \mathrm{~V}}$

27: Predict the products of electrolysis in each of the following: 

(i) An aqueous solution of $\mathrm{AgNO}_{3}$ with silver electrodes

Ans: The reaction between $\mathrm{Ag}$ and $\mathrm{Cu}$ can be described as follows:

At the cathode, electrolysis can decrease either $\mathrm{Ag}^{+}$ions or $\mathrm{H}_{2} \mathrm{O}$ molecules. However, $\mathrm{Ag}^{+}$ions have a larger reduction potential than $\mathrm{H}_{2} \mathrm{O}$

$\mathrm{Ag}_{(\text {aqi }}+\mathrm{e}^{-} \rightarrow \mathrm{Ag}_{(\mathrm{s})} ; \mathrm{E}^{0}=+0.80 \mathrm{~V}$

$2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(2 q)}^{-} ; \mathrm{E}^{0}=-0.83 \mathrm{~V}$

As a result, at the cathode, $\mathrm{Ag}^{+}$ions are decreased. At the anode, $\mathrm{Ag}$ metal or $\mathrm{H}_{2} \mathrm{O}$ molecules can also be oxidised. However, Ag molecules have a larger oxidation potential than $\mathrm{H}_{2} \mathrm{O}$ molecules.

$\mathrm{Ag}_{(\mathrm{s})} \rightarrow \mathrm{Ag}^{+}_{(\mathrm{aq})}+\mathrm{e}^{-} ; \mathrm{E}^{0}=-0.80 \mathrm{~V}$

$2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq})}^{-} ; \mathrm{E}^{0}=-0.83 \mathrm{~V}$

As a result, Ag metal oxidises at the anode.

(ii) An aqueous solution $\mathrm{AgNO}_{3}$ with platinum electrodes

Ans: $\mathrm{Pt}$ is difficult to oxidise. As a result, at the anode, water is oxidised, releasing $\mathrm{O}_{2}$. $\mathrm{Ag}^{+}$ions are reduced and deposited at the cathode.

In aqueous solutions, $\mathrm{H}_{2} \mathrm{SO}_{4}$ ionises to give $\mathrm

(iii) A dilute solution of $\mathrm{H}_{2} \mathrm{SO}_{4}$ with platinum electrodes

Ans: {H}^{+}$and $\mathrm{SO}^{2}{ }_{4}$ ions.

$\mathrm{H}_{2} \mathrm{SO}_{4(\mathrm{aq})} \rightarrow 2 \mathrm{H}_{(\mathrm{aq}}^{+}+\mathrm{SO}^{2-}_{4(\mathrm{aq})}$

At the cathode, electrolysis can decrease either $\mathrm{H}^{+}$ions or $\mathrm{H}_{2} \mathrm{O}$ molecules. $\mathrm{H}^{+}$ions, on the other hand, have a greater reduction potential than $\mathrm{H}_{2} \mathrm{O}$ molecules.

$2 \mathrm{H}_{(\mathrm{aq})}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2(\mathrm{~g})} ; \mathrm{E}^{0}=0.0 \mathrm{~V}$

$2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{aq})}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq})}^{-} ; \mathrm{E}^{0}=0.83 \mathrm{~V}$

As a result, $\mathrm{H}^{+}$ions are reduced at the cathode, releasing $\mathrm{H}_{2}$ gas.

The anode, on the other hand, can oxidise either two $\mathrm{SO}_{4}$ ions or two $\mathrm{H}_{2} \mathrm{O}$ molecules.

However, when $\mathrm{SO}^{2-}{ }_{4}$ is oxidised, more bonds are broken than when $\mathrm{H}_{2} \mathrm{O}$ molecules are oxidised.

As a result, the oxidation potential of $\mathrm{SO}^{2-}{ }_{4}$ ions is lower than that of $\mathrm{H}_{2} \mathrm{O}$. As a result, $\mathrm{H}_{2} \mathrm{O}$ is oxidised at the anode, releasing $\mathrm{O}_{2}$ molecules.

(iv)An aqueous solution of $\mathrm{CuCl}_{2}$ with platinum electrodes.

Ans: $\mathrm{CuCl}_{2}$ ionises in aqueous solutions to produce $\mathrm{Cu}^{2+}$ and $\mathrm{Cl}^{-}$ions as $\mathrm{Cu}^{2+}$ and $\mathrm{Cl}^{-}$ions.

$\mathrm{CuCl}_{2(a q)} \rightarrow \mathrm{Cu}^{2+}{ }_{(\mathrm{aq})}+2 \mathrm{Cl}^{-}$

$\mathrm{Cu}^{2+}$ ions or $\mathrm{H}_{2} \mathrm{O}$ molecules can be reduced at the cathode during electrolysis. $\mathrm{Cu}^{2+}$ on the other hand, has a greater reduction potential than $\mathrm{H}_{2} \mathrm{O}$ molecules.

Similarly, either $\mathrm{Cl}^{-}$or $\mathrm{H}_{2} \mathrm{O}$ is oxidised at the anode. The oxidation potential of $\mathrm{H}_{2} \mathrm{O}$ is greater than the oxidation potential of $\mathrm{Cl}^{-}$.

$2 \mathrm{Cl}_{(\text {aq) }}^{*} \rightarrow \mathrm{Cl}_{2(\mathrm{~g})}+2 \mathrm{e}^{-} ; \mathrm{E}^{0}=-1.36 \mathrm{~V}$

$2 \mathrm{H}_{2} \mathrm{O}_{(1)} \rightarrow \mathrm{O}_{2(\mathrm{~g})}+4 \mathrm{H}_{(2 q)}^{+}+4 \mathrm{e}^{-} ; \mathrm{E}^{0}=-1.23 \mathrm{~V}$

However, due to over-voltage, oxidation of $\mathrm{H}_{2} \mathrm{O}$ molecules occurs at a lower electrode potential than that of $\mathrm{Cl}^{-}$ions (extra voltage required to liberate gas). As a result, at the anode, $\mathrm{Cl}^{-}$ions are oxidised, releasing $\mathrm{Cl}_{2}$ gas.

28: Arrange the following metals in the order in which they displace each other from the solution of their salts.

$\mathrm{Al}, \mathrm{Cu}, \mathrm{Fe}, \mathrm{Mg}$ and $\mathrm{Zh}$

Ans: A metal with a higher reducing power displaces a metal with a lower reducing power from its salt solution.

$\mathrm{Al}, \mathrm{Cu}, \mathrm{Fe}, \mathrm{Mg}$ and $\mathrm{Zn}$ are the metals in order of increasing reducing power. As a result, we can conclude that $\mathrm{Mg}$ can evict $\mathrm{Al}$ from its salt solution, while Al cannot evict $\mathrm{Mg}$. As a result, the following is the sequence in which the supplied metals displace each other from the solution of respective salts:

$\mathrm{Mg}>\mathrm{Al}>\mathrm{Zn}>\mathrm{Fe}>\mathrm{Cu}$

29: Given the standard electrode potentials,

$\mathrm{K}^{+} / \mathrm{K}=-2.93 \mathrm{~V}, \mathrm{Ag}^{+} / \mathrm{Ag}=0.80 \mathrm{~V}$

$\mathrm{Hg}^{+} / \mathrm{Hg}-0.79$

$\mathrm{Mg}^{2+} / \mathrm{Mg}=-2.37 \mathrm{~V} \cdot \mathrm{Cr}^{3+} / \mathrm{Cr}=-0.74 \mathrm{~V}$

Arrange these metals in their increasing order of reducing power.

Ans: The stronger the reducing agent is, the lower the electrode potential. As a result, the reducing power of the above metals is in ascending order: $\mathrm{Ag}>\mathrm{Hg}>\mathrm{Cr}>\mathrm{Mg}>\mathrm{K}$

$\mathrm{Zn}(\mathrm{s})+2 \mathrm{Ag}^{+}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})$

takes place, further show

(i) which of the electrode is negatively charged,

(ii) the carriers of the current in the cell, and

(iii) individual reaction at each electrode.

Ans: The galvanic cell that corresponds to the given redox reaction looks like this:

$\mathrm{Zn}\left[\mathrm{Zn}^{2+}_{(a q)} \| \mathrm{Ag}^{+}_{(a q)}\right] \mathrm{Ag}$

(i) Because $\mathrm{Zn}$ oxidises to $\mathrm{Zn}^{2+}$ at this electrode, the remaining electrons concentrate on it, the Zn electrode is negatively charged.

(ii) Ions are the current carriers in cells.

(iii) The reaction at the Zn electrode can be represented as follows:

$\mathrm{Zn}_{(\mathrm{s})} \rightarrow \mathrm{Zn}^{2+}{ }_{(\mathrm{aq})}+2 \mathrm{e}^{-}$

The reaction at the $\mathrm{Ag}$ electrode can be represented as follows:

$\mathrm{Ag}^{+}{ }_{(\mathrm{aq})}+\mathrm{e}^{\circ} \rightarrow \mathrm{Ag}_{(\mathrm{s})}$

(iv) $\mathrm{CuCl}_{2}$ ionises in aqueous solutions to produce $\mathrm{Cu}^{2+}$ and $\mathrm{Cl}^{-}$ ions as:

$\mathrm{CuCl}_{2(\mathrm{aq})} \rightarrow \mathrm{Cu}^{2+}{ }_{(a q)}+2 \mathrm{Cl}^{-}{ }_{(\mathrm{aq})}$

$\mathrm{Cu}^{2+}$ ions or $\mathrm{H}_{2} \mathrm{O}$ molecules can be reduced at the cathode during electrolysis.

$\mathrm{Cu}^{2+}{ }_{\text {(aq })}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}_{(\mathrm{aq})} ; \mathrm{E}^{0}=+0.34 \mathrm{~V} $

$\mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}^{-} ; \mathrm{E}^{0}=-0.83 \mathrm{~V}$

$\mathrm{Cu}^{2+}$ ions are so reduced and deposited at the cathode.

The oxidation potential of $\mathrm{H}_{2} \mathrm{O}$ is greater than the oxidation potential of $\mathrm{Cl}^{-}$.

$2 \mathrm{Cl}^{-}_{(\mathrm{aq})}+\mathrm{Cl}_{2(\mathrm{H})} \rightarrow 2 \mathrm{e}^{-} ; \mathrm{E}^{0}=-1.36 \mathrm{~V}$

$2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}+\mathrm{O}_{2(\mathrm{~g})} \rightarrow 4 \mathrm{H}^{+}{ }_{2(\mathrm{~g})}+4 \mathrm{e}^{-\cdots} ; \mathrm{E}^{0}=-1.23 \mathrm{~V}$

However, due to over-voltage, oxidation of $\mathrm{H}_{2} \mathrm{O}$ molecules occurs at a lower electrode potential than that of $\mathrm{Cl}^{-}$ions (extra voltage required to liberate gas).

Class 11 Chemistry Chapter 7 Quick Overview of Topics

Chemistry class 11 chapter 7 NCERT Solutions -Quick Overview of Detailed Structure of Topics and Subtopics Covered.

Some Important Concepts Of Chemistry Class 11 Chapter 7 - Redox Reactions

Class 11 NCERT solutions help the students to go through the concepts easily. Here find the Important concepts of Chapter 7 -Redox Reactions to crack your exams.

1. Oxidation Number:

• The oxidation number is the hypothetical charge that an atom would have if all bonds to atoms of different elements were 100% ionic.

• Rules for assigning oxidation numbers help determine whether a species undergoes oxidation or reduction in a reaction.

2. Balancing Redox Reactions:

• Half-Reaction Method: Involves balancing the reduction and oxidation half-reactions separately.

• Ion-Electron Method (or Oxidation-Reduction Method): Balances the redox reaction by dividing it into oxidation and reduction half-reactions and balancing the number of electrons transferred.

3. Oxidizing Agent and Reducing Agent:

• Oxidizing Agent: Substance that gains electrons and undergoes reduction, causing another substance to be oxidized.

• Reducing Agent: Substance that loses electrons and undergoes oxidation, causing another substance to be reduced.

Benefits of Referring to Vedantu’s NCERT Solutions for Class 11 Chemistry Chapter 7

The Vedantu’s Class 11 NCERT Solutions of Chemistry provided here in PDFs offer various benefits, including:

• Detailed explanations and step-by-step solutions for all topics in chapter 7.

• Solutions curated by experienced educators to ensure accuracy and clarity.

• Clear and concise explanations using precise chemical terminology like on the topics half-reaction Method: Involves balancing the reduction and oxidation half-reactions separately.

• In-depth analysis of key concepts and their applications in real-life scenarios.

• Solutions to a variety of problems to strengthen analytical and problem-solving abilities.

• Step-by-step solutions for numerical problems and reaction mechanisms.

• NCERT solutions of Redox reaction class 11 will give you insights about the General Introduction: Concept of oxidation and reduction, redox reactions.

• The section will give you learnings on oxidation number, balancing redox reactions, in terms of loss and gain of electrons and change in oxidation number.

Related Study Materials for Class 11 Chemistry Chapter 7 NCERT Solutions 

Students can access extra study materials on Redox Reactions , These resources are available for download, offering additional support for your studies.

Conclusion

Vedantu has updated NCERT Answers for Redox Reactions in PDF format. These NCERT Answers are created by professional teachers, students may rely on them. In addition, we have included more exam-related questions on this website. These NCERT Answers and critical questions can be used by students to prepare for and revise these topics as this is a scoring chapter once you are expertised in the topic . Vedantu have provided complete resources including chapter notes, important questions and exemplar solutions that will definitely help you aout to score more. 

NCERT Solutions Class 11 Chemistry | Chapter-wise Links 

Access Vedantu’s chapter-wise NCERT Chemistry Class 11 Solutions PDFs below for all other chapters.

Related Important Links for Chemistry Class 11