Question

If $\alpha $,$\beta $,$\gamma $ are the distance of the vertices of a triangle of $ABC$ from the corresponding point of contact with the incircle, then
$(A)$. $s = \alpha + \beta + \gamma $
$(B)$. ${\gamma ^2} = \dfrac{{\alpha \beta \gamma }}{{\alpha + \beta + \gamma }}$
$(C)$. ${\Delta ^2} = \left( {\alpha + \beta + \gamma } \right)\alpha \beta \gamma $
$(D)$. $2s = \alpha + \beta + \gamma $

Answer 1

Hint: Use theorem tangent to the circle to find sides of the triangle and Heron’s formula to compute the area of the triangle.












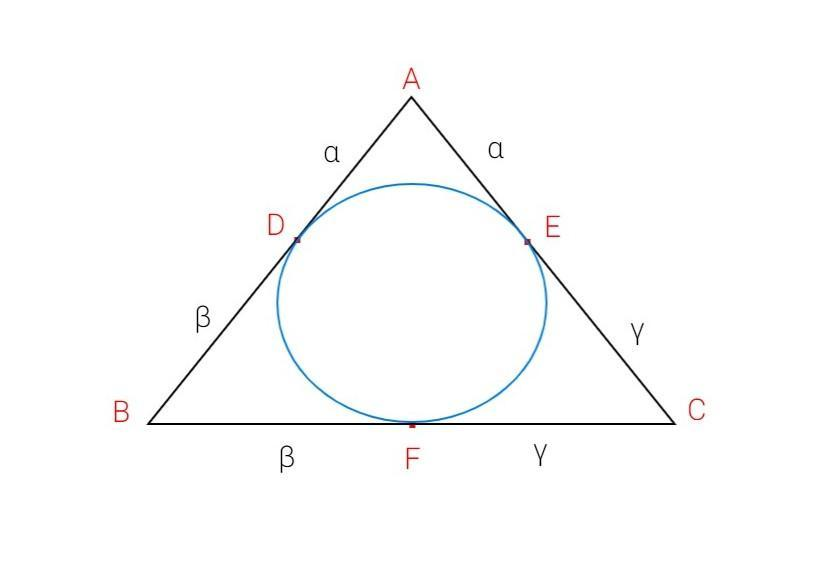
Let ABC be the triangle with incircle inside as given in the problem.
Let the incircle touch the sides of the triangle ABC at points D,E and F respectively .
It is given that $\alpha $,$\beta $,$\gamma $ are the distance of the vertices of a triangle of $ABC$ from the corresponding point of contact with the incircle.
Therefore, we assume,
$
  AD = \alpha \\
  BD = \beta \\
  CE = \gamma \\
 $
Theorem tangent to the circle states that a point external to the circle subtends equal tangents to the circle.
Using this theorem in triangle $ABC$,we get
$
  AE = \alpha \\
  BF = \beta \\
  CF = \gamma \\
$
We need to find the area of the triangle $ABC$ using Heron’s formula.
Heron’s formula states that area of the triangle is given by,
\[\Delta = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} {\text{ (1)}}\]
In the above equation, $s$ is the semi-perimeter of the triangle and $a,b,c$ are the sides of the triangle.
Sides of the triangle $ABC$ are given by
$\left(
  a = AB = \alpha + \beta \\
  b = BC = \beta + \gamma \\
  c = AC = \alpha + \gamma \\
 \right){\text{ (2)}}$
Semi-perimeter of triangle $ABC$ is given by,
$
  s = \dfrac{{a + b + c}}{2} \\
   \Rightarrow s = \dfrac{{\alpha + \beta + \beta + \gamma + \alpha + \gamma }}{2} = \alpha + \beta + \gamma {\text{ (3)}} \\
$
Using equation $(2)$and $(3)$ in $(1)$,we get
\[
  \Delta = \sqrt {\left( {\alpha + \beta + \gamma } \right)\left( {\alpha + \beta + \gamma - \alpha - \beta } \right)\left( {\alpha + \beta + \gamma - \beta - \gamma } \right)\left( {\alpha + \beta + \gamma - \alpha - \gamma } \right)} \\
   \Rightarrow \Delta = \sqrt {\left( {\alpha + \beta + \gamma } \right)\alpha \beta \gamma } {\text{ }} \\
 \]
Squaring both sides of the above equation, we get
\[{\Delta ^2} = \left( {\alpha + \beta + \gamma } \right)\alpha \beta \gamma {\text{ }}\]
Hence option $(C)$. ${\Delta ^2} = \left( {\alpha + \beta + \gamma } \right)\alpha \beta \gamma $ is the correct answer.

Note: Always try to draw the diagram in problems related to incircle. Try to remember the properties of incircle. Geometrical theorems should also be kept in mind while solving similar problems.