




Step-by-Step Calculation of Electric Field for Line Charges and Cylinders
The electric field due to infinite linear charges and cylinders is a fundamental concept in electrostatics, essential for analyzing the behavior of charged systems. Understanding the derivation and computation of electric fields in these symmetric cases is important for solving advanced problems encountered in physics and engineering, especially at the JEE level.
Definition and Concept of Electric Field
An electric field is defined as the region of space around a charged object where another charge experiences a force due to its presence. The direction of the field depends on the nature of the source charge: outward for positive, inward for negative. The field conveys the influence of the charge to its surroundings.
The strength of this field at any point is denoted by electric field intensity, given by $E = \dfrac{F}{q}$, where $F$ is the electrostatic force experienced by a test charge $q$. The SI unit of electric field is newton per coulomb (N/C). Additional context can be found at Understanding Electric Field Intensity.
Gauss’s Law and Its Application
Gauss’s Law is an important relation for evaluating electric fields created by symmetric charge distributions. It states that the total electric flux through a closed surface is equal to the enclosed charge divided by the permittivity of free space, $\varepsilon_0$.
In integral form, Gauss’s Law is written as $\displaystyle \oint \vec{E} \cdot d\vec{A} = \dfrac{Q_{\mathrm{enc}}}{\varepsilon_0}$. The choice of Gaussian surface is determined by the symmetry of the charge arrangement, simplifying calculations for structures such as lines and cylinders.
A detailed overview of Gauss’s Law, electric flux, and electrostatics is provided in the Electrostatics Overview.
Linear Charge Density
Linear charge density is the amount of electric charge per unit length along a line. It is denoted by $\lambda$, and is expressed as $\lambda = \dfrac{Q}{L}$, where $Q$ is the total charge distributed uniformly along length $L$. The SI unit is coulomb per metre (C/m).
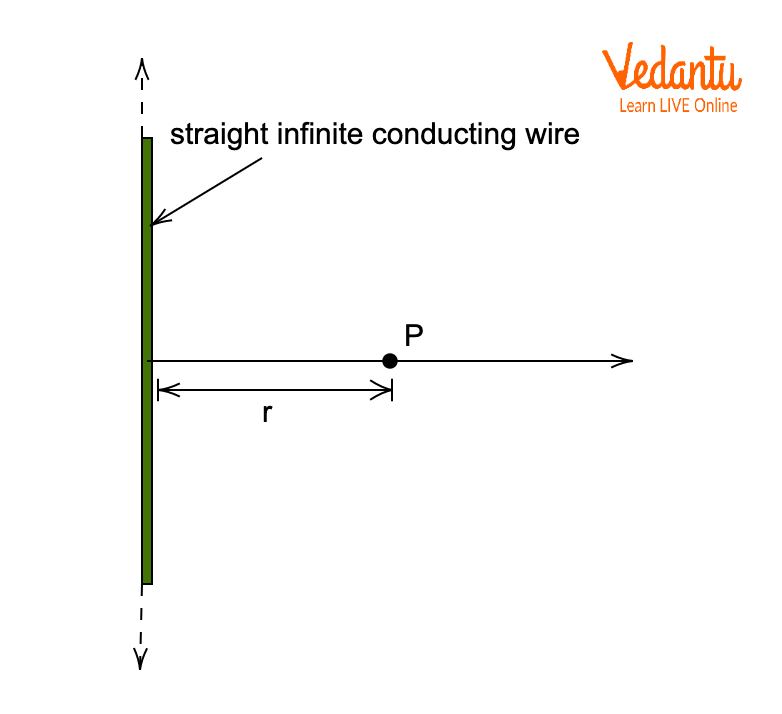
Electric Field Due to an Infinite Line of Charge
For an infinitely long straight line carrying uniform linear charge density $\lambda$, the electric field at a point located at a perpendicular distance $r$ from the wire can be determined using a cylindrical Gaussian surface. This approach leverages the cylindrical symmetry to simplify calculations.
The electric field at distance $r$ from the wire is directed radially outward (or inward) depending on the sign of $\lambda$. The magnitude of the electric field is derived as follows:
The cylindrical Gaussian surface has length $L$ and radius $r$, so the curved surface area is $A = 2\pi rL$. Only the curved surface contributes to the flux, as the electric field is parallel to the normal of the curved surface and perpendicular to the ends.
From Gauss’s Law:
$\displaystyle \oint \vec{E} \cdot d\vec{A} = E \times 2\pi rL = \dfrac{\lambda L}{\varepsilon_0}$
Solving for $E$:
$\displaystyle E = \dfrac{\lambda}{2\pi \varepsilon_0 r}$
This result holds at all points outside an infinite, straight, uniformly charged wire. Field intensity decreases inversely with distance from the wire. Refer to Electric Field Lines and Properties for field visualizations and behavior.
Electric Field Due to an Infinite Cylindrical Shell
An infinite cylinder may be composed of either a thin shell or a solid charged body. If the shell has a uniform surface charge density $\sigma$, the linear charge density becomes $\lambda = 2\pi R \sigma$, where $R$ is the radius of the shell.
For a point outside the cylindrical shell ($r > R$), the electric field is identical to that of an infinite line charge: $E = \dfrac{\lambda}{2\pi \varepsilon_0 r}$. Inside the shell ($r < R$), using Gauss’s Law, the enclosed charge is zero, so the electric field is zero.
| Region | Electric Field |
|---|---|
| Outside cylinder ($r > R$) | $\dfrac{\lambda}{2\pi \varepsilon_0 r}$ |
| Inside cylinder ($r < R$) | $0$ |
Electric Field Due to a Solid Charged Cylinder
If the cylinder is solid and possesses a uniform volume charge density $\rho$, the total charge enclosed within radius $r$ ($r<R$) can be written as $q = \rho \pi r^2 L$. Using this in Gauss’s Law for a Gaussian surface of radius $r$ and length $L$ gives:
$\displaystyle E \cdot 2\pi r L = \dfrac{\rho \pi r^2 L}{\varepsilon_0}$
$\displaystyle E = \dfrac{\rho r}{2\varepsilon_0}$ for $r<R$
Outside the cylinder ($r>R$), total enclosed charge is $q_{\text{total}} = \rho \pi R^2 L$, giving:
$\displaystyle E = \dfrac{\rho R^2}{2\varepsilon_0 r}$ for $r>R$
Key Points and Formulae Summary
- Electric field outside infinite line charge: $E = \dfrac{\lambda}{2\pi \varepsilon_0 r}$
- Outside infinite shell: same as line charge
- Inside conducting shell: field is zero
- Solid cylinder inside: $E = \dfrac{\rho r}{2\varepsilon_0}$
- Solid cylinder outside: $E = \dfrac{\rho R^2}{2\varepsilon_0 r}$
Sample Calculation
Consider a linear charge density $\lambda = 3 \times 10^{-6}$ C/m. The electric field at a point $0.05$ m from the wire in vacuum is given by:
$E = \dfrac{\lambda}{2\pi \varepsilon_0 r} = \dfrac{3 \times 10^{-6}}{2\pi \times 8.85 \times 10^{-12} \times 0.05} \approx 1.08 \times 10^{6}$ N/C$
Physical Interpretation and Applications
The electric field’s magnitude decreases inversely with distance from the wire or cylindrical shell. The inside region of a conducting shell remains field-free, whereas a solid cylinder has a linearly increasing field. The concept is crucial in modeling coaxial cables, capacitors, and charged beams. For capacitive systems using cylindrical symmetry, see Capacitance and Capacitors.
Relation to Electric Field Lines
The direction and density of electric field lines visually represent the electric field’s magnitude and direction. For linear and cylindrical distributions, field lines radiate perpendicular to the surface, demonstrating uniformity in all outward radial directions. More on this topic can be found at Electric Field Lines and Properties.
Related Magnetic Properties
The approach used in determining electric fields using Gauss’s Law in symmetric cases is analogous to methods in magnetism, where Ampère’s Law is used. For related magnetic properties of materials, refer to Magnetic Properties of Materials.
Functional Use in Capacitors and Devices
Cylindrical and coaxial capacitors rely on the principle of electric field due to linear and cylindrical charge distributions for their working. Understanding these distributions aids in calculating capacitance values and analyzing device performance.
FAQs on Understanding the Electric Field Due to Infinite Linear Charge and Cylinders
1. What is the electric field due to an infinite line of charge?
The electric field due to an infinite line of charge is perpendicular to the line and has a constant magnitude at any fixed distance from the line.
• The magnitude of the electric field at distance r from a line with linear charge density λ is:
E = (λ) / (2πε₀r)
• The direction of the electric field is radially outward for positive charge and inward for negative charge.
• This formula uses permittivity of free space (ε₀) and is crucial in CBSE Physics and competitive exams.
• Applicable for solving problems on Gauss's Law and symmetry in electrostatics.
2. How do you find the electric field inside and outside a uniformly charged cylinder?
The electric field in and around a uniformly charged cylinder varies depending on whether the point is inside or outside the cylinder.
• Inside the cylinder (r < R):
E = (λ r) / (2πε₀ R²) (for solid cylinders, where λ is linear charge, r is distance from axis, R is cylinder radius)
• Outside the cylinder (r ≥ R):
E = (λ) / (2πε₀ r)
• For hollow (thin) cylinders, field inside is zero by Gauss's Law.
• The direction is radially outward for positive charge.
• This concept is vital in syllabus topics like Electrostatics, Gauss's Law, and field mapping.
3. How does Gauss’s law help in calculating electric field of a long charged wire?
Gauss’s Law simplifies calculation of the electric field around a long charged wire by utilizing cylindrical symmetry.
• A cylindrical Gaussian surface is chosen around the wire.
• By symmetry, electric field strength E is same at all points at distance r.
• Net flux = E × (surface area of cylinder) = E × (2πrl)
• Total charge enclosed = λ × l
• Using Gauss’s Law: E (2πrl) = (λl)/ε₀ → E = λ/(2πε₀r)
• This matches the standard result for infinite linear charge field.
4. What is the direction of the electric field produced by an infinite line of charge?
The electric field from an infinite line of charge points radially away or towards the wire.
• Direction is radially outward for positive linear charge density (λ > 0).
• Radially inward for negative linear charge.
• At every point, the field is perpendicular to the line and lies in the plane passing through the wire and the point.
• Field lines form concentric circles with the wire at the center.
5. Derive the expression for the electric field near an infinite straight charged rod using Gauss's law.
To derive the electric field near an infinite straight charged rod, use a cylindrical Gaussian surface centered on the rod.
1. Let the rod have charge density λ (C/m).
2. Choose a cylindrical Gaussian surface of radius r and length l.
3. Total charge enclosed = λl.
4. Net electric flux = E × (2πrl).
5. By Gauss's Law, E (2πrl) = λl/ε₀ ⇒ E = λ/(2πε₀r).
• This is the standard textbook derivation required for CBSE board exams.
6. What is the electric field at a point inside a hollow charged cylinder?
The electric field inside a hollow charged cylinder (r < R) is zero everywhere.
• By applying Gauss's Law, no charge is enclosed by a Gaussian surface inside the hollow.
• Therefore, E = 0 at any point within the empty space.
• This is similar to behavior inside a conducting shell.
• Commonly tested in multiple-choice and descriptive exam questions.
7. Why is the electric field inside a conductor zero?
The electric field inside a conductor in electrostatic equilibrium is always zero.
• Free electrons rearrange to cancel any applied field.
• Excess charge resides only on the surface.
• This is a fundamental consequence of electrostatic properties and is crucial for understanding cylindrical shells in CBSE Physics.
8. Compare the electric field due to infinite line charge and infinite plane sheet of charge.
The electric field due to an infinite line charge decreases with distance, while that due to an infinite plane sheet is constant.
• Infinite Line: E = λ/(2πε₀r), field depends on distance (r).
• Infinite Plane: E = σ/(2ε₀), field is independent of distance.
• Both use Gauss’s Law but have different symmetries.
• Frequently compared in CBSE exam syllabi on Electrostatics.
9. What factors affect the magnitude of electric field due to a linear charge?
The magnitude of electric field due to a linear charge mainly depends on:
• Linear charge density (λ): Higher λ → higher field.
• Distance (r) from the wire: Field decreases as 1/r.
• Permittivity of the medium (ε): Field is inversely proportional to ε.
• No field dependence on length for infinite cases.
10. Is the electric field outside a very long charged cylinder the same as that of a line charge?
The electric field outside a very long (thin) charged cylinder is similar to that of an infinite line charge.
• For points outside the cylinder (r > cylinder radius):
E = λ / (2πε₀r)
• The field acts as if all charge is concentrated along the axis.
• This equivalence simplifies many CBSE Physics problems related to cylindrical symmetry and linear charge distributions.

































