JEE Main Physics 2025: Electric Field Intensity Due to Thin Uniformly Charged Infinite Plane Sheet

The electric field due to an infinite plane sheet of charge is a fundamental concept in electrostatics, crucial for understanding many advanced topics in physics, especially for JEE Main 2025. This concept helps in calculating the electric field generated by a uniformly charged infinite sheet, which is vital for solving problems related to electric fields, charge distribution, and Gauss's law. By mastering this topic, you’ll gain a deeper insight into the behaviour of electric fields and be better equipped for your JEE Main physics questions. This guide provides a detailed breakdown of the topic, making it easier to understand and apply in your exam preparation.

What is an Electric Field?

An electric field can be explained to be an invisible field around the charged particles where the electrical force of attraction or repulsion can be experienced by the charged particles. It is also defined as electrical force per unit charge. The SI unit of measurement of electric field is Volt/metre. The formula to determine the electric field is given as 

$E=\dfrac{F}{q}$

Where E is the electric field, F is the electric force and q is the charge.

Since the electric field is an invisible field, we use electric field lines to visualise the electric fields. This concept was introduced by Michael Faraday. The electric field lines are drawn in a tangential direction to the net electric field at a point. 

Some basic properties of Electric field lines are listed below.

1. Electric field lines are always drawn perpendicular to the charge surface.

2. Electric field lines do not intersect each other.

3. Electric field lines start from a positive charge and end at a negative charge.

4. When there is a single charge, if the charge is negative, then the electric field lines start from infinity and end at the charge; and if the charge is positive, then the electric field lines start from the charge and end at infinity.

5. Electric field lines and the magnitude of a charge, these are directly proportional to each other.

Electric Field Due to Infinite Plane Sheet 

The electric field due to an infinite plane sheet of charge is a fundamental concept in electrostatics. It describes the behaviour of the electric field produced by a uniformly charged plane that extends infinitely in all directions. Understanding this electric field is essential for solving many problems in electrostatics, particularly when using Gauss's law.

Key Points on The Electric Field Due to An Infinite Plane Sheet

• Uniform Electric Field: The electric field generated by an infinite plane sheet of charge is uniform and has the same magnitude at all points, regardless of the distance from the sheet. This is different from other charge distributions, where the electric field strength decreases with distance.

• Direction of the Electric Field: The electric field lines are always perpendicular to the surface of the sheet, pointing away from the sheet if the charge is positive and toward the sheet if the charge is negative.

• Magnitude of the Electric Field: The electric field due to an infinite sheet of charge is constant and does not depend on the distance from the sheet. It can be calculated using Gauss’s law as:
  $E = \dfrac{\sigma}{2 \epsilon_0}$
  where E is the electric field, $\sigma$ is the surface charge density (charge per unit area), and $\epsilon_0$​ is the permittivity of free space.

• Independence from Distance: Unlike point charges or spherical charge distributions, the electric field of an infinite sheet does not decrease with distance. It remains constant at any point in space.

Derivation Using Gauss’ Law

In electrostatics, we study about the electric charges at rest. The electric charges form an electric field around them, thus affecting the properties in the environment surrounding the charges. The electric field is stated to be a property of a charged system. A mathematician named Karl Friedrich Gauss (1777-1855), formulated a law known as Gauss’ law. This law explains the connection between electric fields and the electric charges. Gauss’ law helps to determine the intensity of electric fields due to various charged surfaces.

The statement of Gauss’ Law is that “The total flux contained within a closed surface equals 1/ε0 times the total electric charge enclosed by the closed surface.” According to Gauss' theorem, we know that ‘Within a closed surface, the net electric charge is  proportional to total electric flux enclosed by the surface. Thus, if φ represents the total electric flux and if the electric permittivity constant is ε0, the net electric charge is represented by Q (enclosed within the surface), then, we have

$Q=\phi {{\varepsilon }_{0}}$

Therefore, the formula for Gauss’ law is expressed in the terms of net electric charge as

$\phi =\dfrac{Q}{{{\varepsilon }_{0}}}$

where,

• Q represents the net charge enclosed by a given specific surface, and

• ${{\varepsilon }_{0}}$ is the electric permittivity constant.

This law explains that the net electric flux through a closed surface depends on the total electric charge contained in the volume within the surface.

Electric Field Due to Uniformly Charged Infinite Plane Sheet Derivation

Let us consider a charged infinite plane sheet and the charges are uniformly distributed on the sheet. Let P be any  arbitrary point at ‘r’ distance from the sheet. Since, the plane is considered to be infinitely large. Therefore, the electric field at all the points equidistant from the plane sheet would be the same and it would be radially directed at all the points. 

Now, we consider a hypothetical cylindrical surface of length ‘2r’ and area of the plane surface be ‘A’. We assume that the sheet passes through the middle of this surface and is perpendicular to it. This hypothetical closed surface is known as the Gaussian Surface. The above situation is explained in the diagram given below.

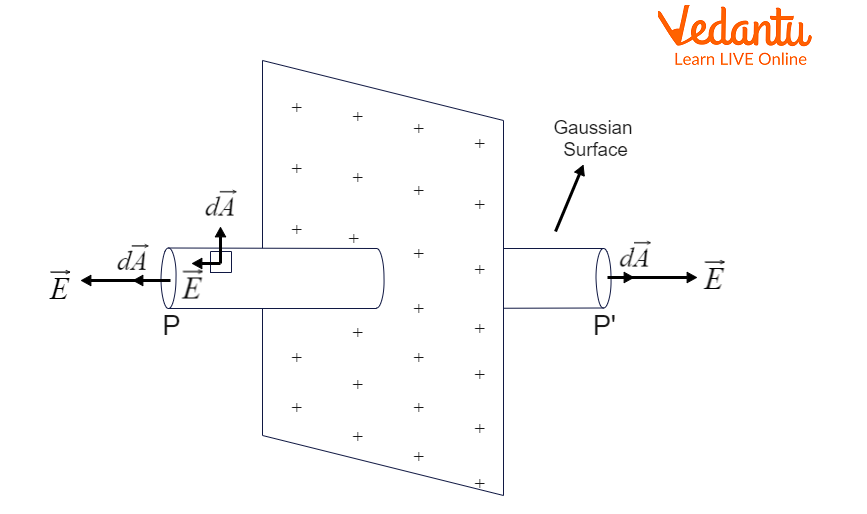
Gaussian Surface for Uniformly Charged Infinite Plane Sheet

Now, we apply the Gauss’ Law to the hypothetical Gaussian Surface in the above diagram. The net electric flux through the surface will be determined by integrating the product of electric field E and and the area element dA, i.e. 

$\begin{align}& {{\phi }_{E}}=\oint{E\cdot dA} \\ & \Rightarrow {{\phi }_{E}}=\int{E\cdot dA}+\int\limits_{P}{E\cdot dA}+\int\limits_{P'}{E\cdot dA} \\ \end{align}$

Since the electric field is directed normally to the area element for all the points on the curved surface and is directed in the same direction to the area element on the plane surfaces P and P’, we have 

${{\phi }_{E}}=0+\int\limits_{P}{E\cdot dA}+\int\limits_{P'}{E\cdot dA}$

It will be equal to the charged enclosed within the surface divided by the electric constant ${{\varepsilon }_{0}}$ i.e. 

${{\phi }_{E}}=0+\int\limits_{P}{E\cdot dA}+\int\limits_{P'}{E\cdot dA}=\dfrac{Q}{{{\varepsilon }_{0}}}$

The electric field is uniform through the surface, therefore, we take E out of integration. The charge enclosed can be replaced with the product of charge density and total area of the surface. If $\sigma $ denotes the surface charge density and ‘A’ is the total surface area, then we have 

$\begin{align}& 2E\int\limits_{P}{dA=\dfrac{\sigma A}{{{\varepsilon }_{0}}}} \\ & \Rightarrow 2EA=\dfrac{\sigma A}{{{\varepsilon }_{0}}} \\ & \Rightarrow E=\dfrac{\sigma }{2{{\varepsilon }_{0}}} \\ \end{align}$

In vector form, the above equation can be written as 

$E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}\hat{n}$

Here, $\hat{n}$ is the unit vector in the direction perpendicular to the plane. We can observe from the equation that the electric field due a uniformly charged infinite plane sheet is proportional to the surface charge density of the plane sheet and does not depend on the distance ‘r’ from the plane. 

The electric field at any point away from the plane will be the same, since the charge density will remain constant for a uniformly charged plane. From the above equation, we can conclude that if the surface charge density, $\sigma >0$ then the electric field will be directed outwards perpendicular to the plane, and if it is negative, i.e. $\sigma <0$, then the electric field is directed inwards perpendicular to the plane. If the above plane sheet were considered finite, then the equation would be valid only for the area in the middle of the sheet.

Electric Field Inside a Spherical Shell (Gauss's Law)

One of the most interesting and important results in electrostatics is that the electric field inside a spherical shell of charge is zero. This is a direct consequence of Gauss's Law.

Key Points:

1. Symmetry:

• Inside the shell, every point is symmetrically surrounded by the shell, and because of this symmetry, there is no net electric field produced by the charge distribution on the shell. Essentially, the electric fields produced by different parts of the shell cancel each other out.

2. Electric Field Inside the Shell:

• For any point inside the spherical shell, the electric field is zero, regardless of the distance from the center, as long as the point is within the shell (i.e., r<R).

3. This result can be derived using Gauss's Law by considering a Gaussian surface inside the shell (a sphere of radius r where r<R). Since there is no enclosed charge within this Gaussian surface, the net electric flux through the surface is zero. Thus, the electric field must also be zero inside the shell.
   $E_{\text{inside}} = 0$

Summary

The electric field is defined as the electrical force per unit charge. The SI unit of measurement of an electric field is Volt/metre. The statement of Gauss’ Law mentions that “The total flux contained within a closed surface equals 1/ε0 times the total electric charge enclosed by the closed surface.” It is formulated as $\phi =\dfrac{Q}{{{\varepsilon }_{0}}}$.

The electric field due to conducting sheet is given by $E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}\hat{n}$ where E is the Electric field, $\sigma $ is the surface charge density and ${{\varepsilon }_{0}}$ is the electric constant. The electric field at any point away from the plane will be the same.

JEE Main 2025 Subject-wise Important Chapters

The JEE Main 2025 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.

Important Links for JEE Main and Advanced 2025

Access a curated collection of study materials and tips to excel in JEE Main and Advanced 2025, helping you prepare effectively for these prestigious engineering entrance exams.