Question

Prove that the locus of the poles of chords which subtend a right angle at a fixed point \[\left( h,k \right)\] is \[a{{x}^{2}}-h{{y}^{2}}+\left( 4{{a}^{2}}+2ah \right)x-2aky+a\left( {{h}^{2}}+{{k}^{2}} \right)=0\]

Answer 1

Hint: Equation of chord joint two points \[\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[\left( at_{2}^{2},2a{{t}_{2}} \right)\] on a parabola is given as
\[\left( {{t}_{1}}+{{t}_{2}} \right)y=2x+2a{{t}_{1}}{{t}_{2}}\] , where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.

And , the equation of chord of parabola \[{{y}^{2}}=4ax\] with respect to pole \[(p,q)\] is given as \[yq=2a\left( x+p \right)\].
We will consider the equation of the parabola to be \[{{y}^{2}}=4ax\]
Now, we are asked to find the locus of the poles.
So , we will consider the pole to be \[A\left( {{x}_{1}},{{y}_{1}} \right)\].
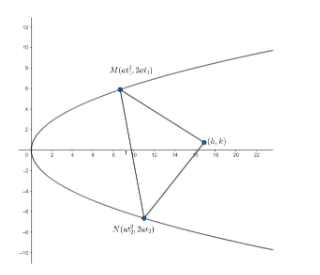
Let us take the point of contact of chord as \[M\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[N\left( at_{2}^{2},2a{{t}_{2}} \right)\] , where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.
Now , we need to find the equation of chord.
We know , the equation of chord of parabola \[{{y}^{2}}=4ax\] with respect to pole \[(p,q)\] is given as \[yq=2a\left( x+p \right)\].

So , the equation of chord with respect to \[A\]is \[y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)....\left( i \right)\]
Now , we also know that the equation of chord joining the points \[(at_{1}^{2},2a{{t}_{1}})\] and \[(at_{2}^{2},2a{{t}_{2}})\] is given as \[\left( {{t}_{1}}+{{t}_{2}} \right)y=2x+2a{{t}_{1}}{{t}_{2}}\]
So , the equation of chord joining \[M.N\] is \[\left( {{t}_{1}}+{{t}_{2}} \right)y=2x+2a{{t}_{1}}{{t}_{2}}....\left( ii \right)\]
Now, we know both these chords are the same.
We also know that if two equations \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]are same then , \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\]
So , \[\dfrac{\text{coefficient of }x\text{ in eqn }(i)}{\text{coefficient of }x\text{ in eqn }(ii)}=\dfrac{\text{coefficient of }y\text{ in eqn }(i)}{\text{coefficient of }y\text{ in eqn }(ii)}=\dfrac{\text{constant in }(i)}{\text{constant in }(ii)}\]
Or , \[\dfrac{2a}{2}=\dfrac{-{{y}_{1}}}{-\left( {{t}_{1}}+{{t}_{2}} \right)}=\dfrac{2a{{x}_{1}}}{2a{{t}_{1}}{{t}_{2}}}\]
\[\Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)=\dfrac{{{y}_{1}}}{a}....\left( iii \right)\]
and \[{{t}_{1}}{{t}_{2}}=\dfrac{{{x}_{1}}}{a}....\left( iv \right)\]
Now , the chords subtend a right angle at \[\left( h,k \right)\].
We know , if two lines are perpendicular , then the product of their slopes \[=-1\].
So, the product of slopes of the lines joining the extremities of the chord and \[\left( h,k \right)\]\[=-1\].
Now , we know , the slope of the line joining two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is given as \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
So, \[\dfrac{k-2a{{t}_{1}}}{h-at_{1}^{2}}\times \dfrac{k-2a{{t}_{2}}}{h-at_{2}^{2}}=-1\]
\[\Rightarrow {{k}^{2}}-2ak\left( {{t}_{1}}+{{t}_{2}} \right)+4{{a}^{2}}{{t}_{1}}{{t}_{2}}=-\left[ {{h}^{2}}-ah\left( t_{1}^{2}+t_{2}^{2} \right)+{{a}^{2}}t_{1}^{2}t_{2}^{2} \right]\]
\[\Rightarrow {{k}^{2}}-2ak\left( {{t}_{1}}+{{t}_{2}} \right)+4{{a}^{2}}{{t}_{1}}{{t}_{2}}=-\left[ {{h}^{2}}-ah\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}} \right)+{{a}^{2}}t_{1}^{2}t_{2}^{2} \right]....\left( v \right)\]
Now substituting \[\left( iii \right)\]and \[\left( iv \right)\] in equation \[\left( v \right)\] we get,
\[{{k}^{2}}-2ak.\dfrac{{{y}_{1}}}{a}+4{{a}^{2}}\dfrac{{{x}_{1}}}{a}=-\left[ {{h}^{2}}-ah\left( {{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-2\dfrac{{{x}_{1}}}{a} \right)+{{a}^{2}}{{\left( \dfrac{{{x}_{1}}}{a} \right)}^{2}} \right]\]
\[\Rightarrow {{k}^{2}}-2k{{y}_{1}}+4{{x}_{1}}a=-\left[ {{h}^{2}}-\dfrac{h}{a}\left( y_{1}^{2}-2a{{x}_{1}} \right)+x_{1}^{2} \right]\]
\[\Rightarrow a{{k}^{2}}-2ak{{y}_{1}}+4{{a}^{2}}{{x}_{1}}=-a{{h}^{2}}+hy_{1}^{2}-2ah{{x}_{1}}-ax_{1}^{2}\]
\[\Rightarrow ax_{1}^{2}-hy_{1}^{2}+\left( 4{{a}^{2}}+2ah \right){{x}_{1}}-2ak{{y}_{1}}+a\left( {{k}^{2}}+{{h}^{2}} \right)=0.......\] equation\[(vi)\]
Now, to find the locus of \[A\left( {{x}_{1}},{{y}_{1}} \right)\], we will substitute \[(x,y)\]in place of \[\left( {{x}_{1}},{{y}_{1}} \right)\] in equation \[(vi)\]
So, the equation of locus of \[A\left( {{x}_{1}},{{y}_{1}} \right)\] is given as
\[a{{x}^{2}}-h{{y}^{2}}+\left( 4{{a}^{2}}+2ah \right)x-2aky+a\left( {{k}^{2}}+{{h}^{2}} \right)=0\]

Note: : While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .