Question

Rays of light from Sun falls on a biconvex lens of focal length f and the circular image of Sun of radius r is formed on the focal plane of the lens. Then
A. Area of image is $πr^2$ and area is directly proportional of f
B. Area of image is $πr^2$ and area is directly proportional of $f^2$
C. Intensity of image increases if f is increased
D. If lower half of the lens is covered with black paper area will become half

Answer 1

Hint: In this question we will use the concept of refraction through biconvex lens and focal plane. The biconvex lens is a straightforward lens made up of two convex surfaces that are spherical in shape and typically have the same radius of curvature.

Formula used:
In a triangle, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$

Complete step by step solution:
Let the focus of the biconvex lens be A, the centre of the biconvex lens be C and the point diametrically opposite to A on the reflection be B. The angle at which sun rays hit the biconvex lens is α and the angle after reflection is β.

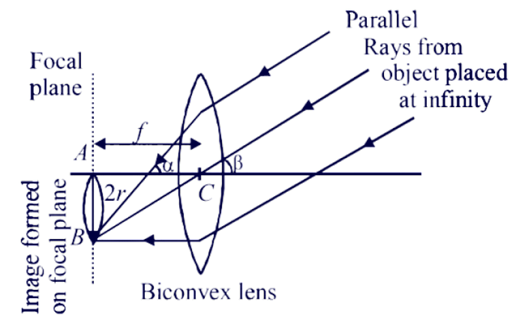
In triangle ABC,
$Tan\beta =\dfrac{AB}{AC}=\dfrac{2r}{f}$
$\Rightarrow r=\dfrac{f}{2}\tan \beta $
$\Rightarrow r\propto f$
$\Rightarrow {{r}^{2}}\propto {{f}^{2}}$ - (1)
Area of the image = $πr^2$ and from equation (1), it is directly proportional to $f^2$.

Hence, the correct answer is B.

Additional Information: A biconvex lens is a type of simple lens that consists of two convex surfaces that are spherical in shape and often have the same radius of curvature. They can also be referred to as convex-convex lenses. A collimated or perfectly parallel light beam travels through a biconvex lens and converges to a point or focus that is behind the lens. There will be about two focal points and two centres because the lens is curved on both sides. The principal axis is the line that passes through the centre of a biconvex lens.

Note: After refraction the angle should change and all the rays should converge at the focal point. Sun is taken to be at an infinite distance.