Question

When the switch \[S\] , in the circuit shows, is closed, then the value of current \[i\] will be:
     
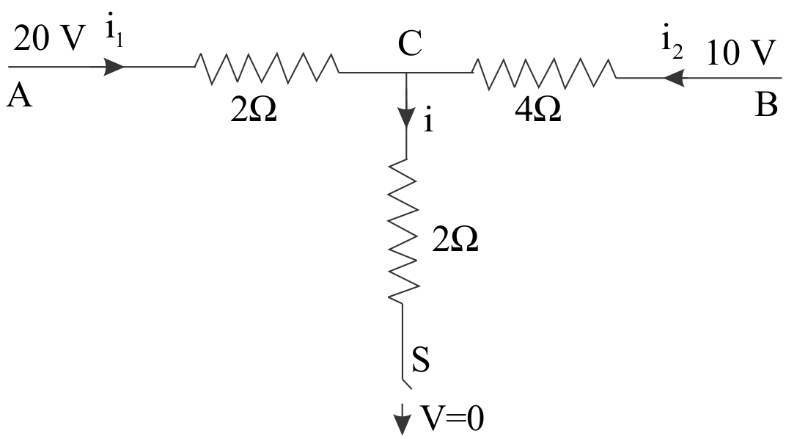
(A) \[3A\]
(B) \[5A\]
(C) \[4A\]
(D) \[2A\]

Answer 1

Hint: Let the potential across terminal C be \[xV\] and apply the Kirchoff’s Current Law at point C i.e. the current incoming is equal to the current outgoing . And first find the value of \[x\] and this will ultimately help us in finding the value of \[i\] .

Complete step by step solution:
          

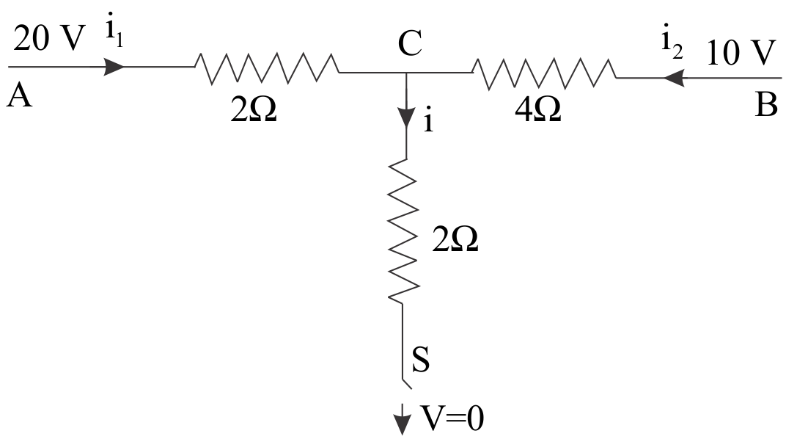
One end of the terminal C is grounded as we can clearly see and it has a potential of zero volts. As soon as the switch is closed the current will start running in that arm and we are required to find that value .
Let the potential at point C be \[xV\] .
At point C , we will apply Kirchoff’s First Law or we can say Kirchoff’s Current law which states that: the sum of currents entering the junction is equal to the sum of currents leaving the junction . It is based on the principle of conservation of charge.
This means that: \[i = {i_1} + {i_2}\] ……..(i)
We know from Ohm’s Law that -
\[
  current = \dfrac{{voltage}}{
  resistor \\
    \\
 } \\
  i = \dfrac{V}{R} \\
 \]

Writing the respective values of \[i,{i_1},{i_2}\] in eq(i) in terms of voltage and resistance across them .
\[
  i = {i_1} + {i_2} \\
  \dfrac{{x - 0}}{2} = \dfrac{{20 - x}}{2} + \dfrac{{10 - x}}{4} \\
  2x = (40 - 2x) + (10 - x) \\
  2x + 2x + x = 50 \\
  5x = 50 \\
  x = 10V \\
 \]
Now we know that-
\[
  i = \dfrac{{x - 0}}{2} \\
  i = \dfrac{{10}}{2} \\
  i = 5A \\
 \]
Hence, the correct option is B.

Note: We have to keep in mind that we have taken $x$ as the potential across C and not potential drop ( which is the difference in potential between two points) while in the ohm’s law we always take potential difference across any two terminals . So that is why while writing the values of current we have written potential differences.