Question

The body of mass $M$ tied to a string is lowered down at a constant acceleration of $\dfrac{g}{4}$ along a vertical distance $h$ then the work done by the string is
(A) $\dfrac{3}{4}Mgh$
(B) $\dfrac{1}{4}Mgh$
(C) $\dfrac{{ - 3}}{4}Mgh$
(D) $\dfrac{{ - 1}}{4}Mgh$

Answer 1

Hint: Work done is defined as the measure of energy transfer, occurring when a certain object moves over a distance when an external force is applied in the direction of displacement. In other words, work done is also defined as the product of tension and displacement.

Complete step by step solution
Let the acceleration of the gravity be $g$ and tension be $T$.
Consider all the forces acting on a string in the following figure:

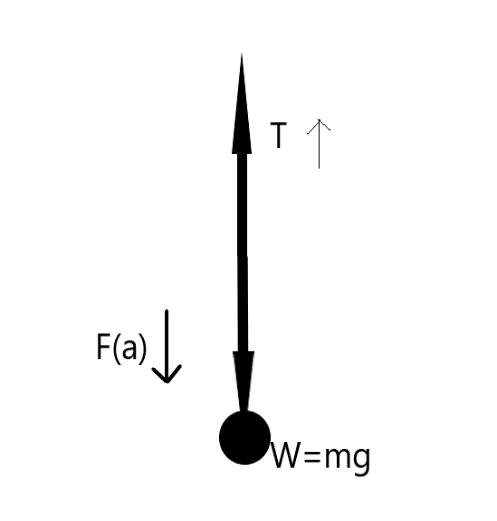
Weight of the body, that is, $mg$ in the downward direction, tension is in the upward direction and accelerating force applies in the downward direction.
1. Tension force is the pulling force which is transmitted axially through the string, cable, etc.
2. Weight is measured with reference to the gravity of the earth, thus it always applies in the downward direction of the object.
3. Accelerating force is a force that causes accelerated motion. It is defined as the product of mass and acceleration.

Now balance all the force acting on it,
$ \Rightarrow W - T = F\left( a \right)$
Substitute the value of $W$and $F\left( a \right)$.
$ \Rightarrow mg - T = ma$
Substitute the value of constant acceleration.
$ \Rightarrow mg - T = \dfrac{{mg}}{4}$
1. Take the same coefficient to one side of the equation.
2. Write the tension in terms of mass and acceleration due to gravity, take LCM of the denominator to determine the value.
$ \Rightarrow T = mg - \dfrac{{mg}}{4} = \dfrac{3}{4}mg$
Work done by tension in the string when the object is lowered down at a distance $h$ is,
$ \Rightarrow W = T \cdot h$
$ = Th\cos {180^ \circ }$
$ = - T \cdot h$
Substitute the value of tension in the above equation.
$ \Rightarrow W = - \dfrac{3}{4}Mg \cdot h$
$ = - \dfrac{3}{4}Mgh$

So, option (3) is the correct answer.

Note:
The work done is defined as a product of tension and displacement. While calculating the displacement, must remember that whether it is opposite to the tension force or in the direction. For balancing of force acting on a body direction is necessary.