Question

The centroid of a triangle is the point of concurrence of its:
A. Angle bisectors
B. Perpendicular bisectors
C. Altitudes
D. Medians

Answer 1

Hint: First of all find the meaning of angle bisectors, perpendicular bisectors, altitudes and medians. Apply the definitions of centroid, orthocenter, circumcenter and incenter of a triangle. From the definition of centroid, it is the point where all the medians of a triangle intersects.

Complete step by step answer
As we know, angle bisectors are lines that divide the angle of a triangle in two equal parts such as in the figure below, line $AD$ is dividing $\angle A$ in two parts.



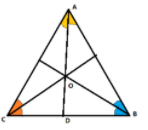
The point where all the angle bisectors of the triangle meet is known as the incenter of the triangle.

Perpendicular bisector from a vertex divide the opposite side in two equal parts and makes an angle of ${90^ \circ }$



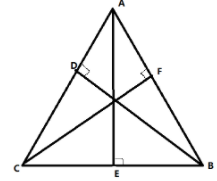
In the above figure, $AE \bot BC$ and $CE = EB$, therefore, $AE$ is a perpendicular bisector.
The point where perpendicular bisectors meet is known as the circumcenter of the triangle.
Altitude from a vertex makes an angle of ${90^ \circ }$ on the opposite side.



For example, the line $AE$ which makes a right angle from vertex $A$ on line $BC$, hence $AE$ is an altitude.
The point where the altitudes meet in a triangle is known as the orthocenter.
Medians are the lines that bisect the sides of the triangle.



The line $AE$ divides line $BC$ into equal parts, hence is the median.
When medians meet at a point, it is known as the centroid.
Therefore, the centroid of a triangle is the point of concurrence of its medians.
Hence, option D is correct.

Note: Median bisects the opposite side and not the angle from which it is drawn. The lines that divide the angle of a triangle in two equal parts are angle bisectors. In a triangle, the centroid divides the median in 2:1 from the vertex the median is drawn. The centroid of a triangle always lies inside the triangle.