Answer
Verified109.5k+ views
Hint: Maximum angle of the incline so that the block does not slip will be obtained when the friction force opposing it’s slipping will be almost equal to the component of its weight along the incline.
Frictional force on the block when angle will be $\dfrac{\theta }{2}$ , will be equal to its weight component at that moment along the incline.
Complete step by step solution:
The maximum angle $\theta $ of the incline with the horizontal so that the block does not slip on the plane will be the condition when the block will just about to slip. So at that point, static friction will be working at its peak.
At the time, when the block is about to slip, friction force on the block in upwards direction will be equal to the component of weight of block.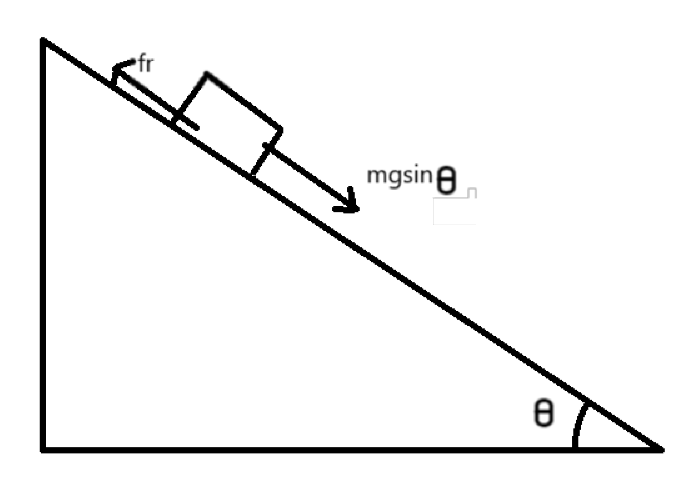
This friction force is equal to the multiplication of coefficient of static friction and the normal force acting on the block.
Normal force acting on the block is $\cos $ component of weight.
So normal force is $mg\cos \theta $
Friction force acting on the block at this condition will be $\mu mg\cos \theta $
Since, this is equivalent to $mg\sin \theta $ ,
Therefore, $mg\sin \theta = \mu mg\cos \theta $ ,
On simplifying this we get,
$\sin \theta = \mu \cos \theta $
So we get,
$\dfrac{{\sin \theta }}{{\cos \theta }} = \mu $ ,
Hence, $\tan \theta = \mu $
So we get our answer as, $\theta = {\tan ^{ - 1}}\mu $ ,
Putting, value of coefficient of friction in above equation we get,
$\theta = {\tan ^{ - 1}}\left( {0.3} \right)$
Hence, when the $\theta = {\tan ^{ - 1}}\left( {0.3} \right)$ , the block will be about to slip.
When the angle of inclination will be $\theta ' = \dfrac{\theta }{2}$ ,
The frictional force acting on the block will be equal to the component of weight of block along the incline which is $mg\sin \theta '$ .
So, ${\text{Frictional Force = mg sin}}\theta '$
On putting value of $\theta ' = \dfrac{\theta }{2}$ in above equation we get,
${\text{Frictional Force = mg sin}}\left( {\dfrac{\theta }{2}} \right)$ ,
Note: Since, we got $\theta = {\tan ^{ - 1}}\mu $ , for the block which is just about to slip from the incline place, therefore, we can observe that this angle does not depend on the mass of the block, it only depends on the incline angle of wedge. In the second example, frictional force will not be equal to the multiplication of coefficient of static friction and the normal force acting on the block because it is not at its peak, rather it’s only balancing the weight component of the block along the incline.
Frictional force on the block when angle will be $\dfrac{\theta }{2}$ , will be equal to its weight component at that moment along the incline.
Complete step by step solution:
The maximum angle $\theta $ of the incline with the horizontal so that the block does not slip on the plane will be the condition when the block will just about to slip. So at that point, static friction will be working at its peak.
At the time, when the block is about to slip, friction force on the block in upwards direction will be equal to the component of weight of block.
This friction force is equal to the multiplication of coefficient of static friction and the normal force acting on the block.
Normal force acting on the block is $\cos $ component of weight.
So normal force is $mg\cos \theta $
Friction force acting on the block at this condition will be $\mu mg\cos \theta $
Since, this is equivalent to $mg\sin \theta $ ,
Therefore, $mg\sin \theta = \mu mg\cos \theta $ ,
On simplifying this we get,
$\sin \theta = \mu \cos \theta $
So we get,
$\dfrac{{\sin \theta }}{{\cos \theta }} = \mu $ ,
Hence, $\tan \theta = \mu $
So we get our answer as, $\theta = {\tan ^{ - 1}}\mu $ ,
Putting, value of coefficient of friction in above equation we get,
$\theta = {\tan ^{ - 1}}\left( {0.3} \right)$
Hence, when the $\theta = {\tan ^{ - 1}}\left( {0.3} \right)$ , the block will be about to slip.
When the angle of inclination will be $\theta ' = \dfrac{\theta }{2}$ ,
The frictional force acting on the block will be equal to the component of weight of block along the incline which is $mg\sin \theta '$ .
So, ${\text{Frictional Force = mg sin}}\theta '$
On putting value of $\theta ' = \dfrac{\theta }{2}$ in above equation we get,
${\text{Frictional Force = mg sin}}\left( {\dfrac{\theta }{2}} \right)$ ,
Note: Since, we got $\theta = {\tan ^{ - 1}}\mu $ , for the block which is just about to slip from the incline place, therefore, we can observe that this angle does not depend on the mass of the block, it only depends on the incline angle of wedge. In the second example, frictional force will not be equal to the multiplication of coefficient of static friction and the normal force acting on the block because it is not at its peak, rather it’s only balancing the weight component of the block along the incline.
Recently Updated Pages
If x2 hx 21 0x2 3hx + 35 0h 0 has a common root then class 10 maths JEE_Main
The radius of a sector is 12 cm and the angle is 120circ class 10 maths JEE_Main
For what value of x function fleft x right x4 4x3 + class 10 maths JEE_Main
What is the area under the curve yx+x1 betweenx0 and class 10 maths JEE_Main
The volume of a sphere is dfrac43pi r3 cubic units class 10 maths JEE_Main
Which of the following is a good conductor of electricity class 10 chemistry JEE_Main