
Answer
110.7k+ views
Hint: The above problem is based on the vector subtraction and relative velocity concept. Airplane is heading towards north and wind is blowing towards east which means that velocity of airplane with respect to ground can be calculated by subtracting magnitude of velocity shown by speedometer and velocity of wind. Let’s get started with the vector subtraction to find out the speed of the plane with respect to round.
Complete step by step solution:
First let’s discuss vectors and relative velocity concepts in detail.
Vectors quantities are those which are characterised by both magnitude and direction. Vectors are represented by a line with an arrow head (which represents the direction of the vector).
Vector subtraction: The process of subtraction of one algebraic quantity from another is equivalent to adding the negative of the quantity to be subtracted.
The relative velocity is the velocity of an object or observer B in the rest frame of another object or observer A. Now, we calculate the velocity of the plane with respect to ground.
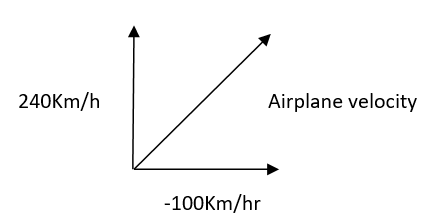
We will do vector subtraction by using the concept of Pythagoras theorem.
Velocity of an airplane will be denoted by $V_{ag}$ velocity of wind is $V_W$ and velocity of airplane $V_a$.
$
\Rightarrow {V^2}_{ag} = {V_a}^2 + {V_w}^2 \\
\Rightarrow {V_{ag}} = \sqrt {{V_a}^2 + {V_w}^2} \\
\Rightarrow {V_{ag}} = \sqrt {{{(240)}^2} + {{(100)}^2}} \\
$ (We have used the formula and substituted the value of velocities)
$
\Rightarrow {V_{ag}} = \sqrt {67600} \\
\Rightarrow {V_{ag}} = 260Km/hr \\
$ (We have done the square and added the value)
To find the angle of movement of airplane we will use
$
\Rightarrow \tan \theta = \dfrac{{{V_w}}}{{{V_a}}} \\
\Rightarrow \tan \theta = \dfrac{{100}}{{240}} \\
$ (We have use the tangent formula)
$
\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{{100}}{{240}} \\
\Rightarrow \theta = 22.67 \\
\Rightarrow \theta = {23^0} \\
$
Option (A) is correct.
Note: Vector addition and subtraction can be done using two laws which are: parallelogram law of vector addition and triangle law of vector addition. In the triangle law of vector addition, the head of one vector is attached to the tail of another vector.
Complete step by step solution:
First let’s discuss vectors and relative velocity concepts in detail.
Vectors quantities are those which are characterised by both magnitude and direction. Vectors are represented by a line with an arrow head (which represents the direction of the vector).
Vector subtraction: The process of subtraction of one algebraic quantity from another is equivalent to adding the negative of the quantity to be subtracted.
The relative velocity is the velocity of an object or observer B in the rest frame of another object or observer A. Now, we calculate the velocity of the plane with respect to ground.

We will do vector subtraction by using the concept of Pythagoras theorem.
Velocity of an airplane will be denoted by $V_{ag}$ velocity of wind is $V_W$ and velocity of airplane $V_a$.
$
\Rightarrow {V^2}_{ag} = {V_a}^2 + {V_w}^2 \\
\Rightarrow {V_{ag}} = \sqrt {{V_a}^2 + {V_w}^2} \\
\Rightarrow {V_{ag}} = \sqrt {{{(240)}^2} + {{(100)}^2}} \\
$ (We have used the formula and substituted the value of velocities)
$
\Rightarrow {V_{ag}} = \sqrt {67600} \\
\Rightarrow {V_{ag}} = 260Km/hr \\
$ (We have done the square and added the value)
To find the angle of movement of airplane we will use
$
\Rightarrow \tan \theta = \dfrac{{{V_w}}}{{{V_a}}} \\
\Rightarrow \tan \theta = \dfrac{{100}}{{240}} \\
$ (We have use the tangent formula)
$
\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{{100}}{{240}} \\
\Rightarrow \theta = 22.67 \\
\Rightarrow \theta = {23^0} \\
$
Option (A) is correct.
Note: Vector addition and subtraction can be done using two laws which are: parallelogram law of vector addition and triangle law of vector addition. In the triangle law of vector addition, the head of one vector is attached to the tail of another vector.
Recently Updated Pages
Write an article on the need and importance of sports class 10 english JEE_Main

Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

If x2 hx 21 0x2 3hx + 35 0h 0 has a common root then class 10 maths JEE_Main

The radius of a sector is 12 cm and the angle is 120circ class 10 maths JEE_Main

For what value of x function fleft x right x4 4x3 + class 10 maths JEE_Main

Other Pages
If a wire of resistance R is stretched to double of class 12 physics JEE_Main

The energy stored is a condenser is in the form of class 12 physics JEE_Main

Excluding stoppages the speed of a bus is 54 kmph and class 11 maths JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

In Searles apparatus when the experimental wire is class 11 physics JEE_Main




