Question

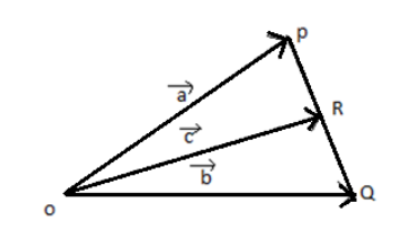
The figure shows the vectors$\overrightarrow a $, $\overrightarrow b $ and$\overrightarrow c $. Where (R) is the midpoint of (PQ). Which of the following relations is correct?


(A) $\overrightarrow a + \overrightarrow b = 2\overrightarrow c $
(B) $\overrightarrow a + \overrightarrow b = \overrightarrow c $
(C) $\overrightarrow a - \overrightarrow b = 2\overrightarrow c $
(D) $\overrightarrow a - \overrightarrow b = \overrightarrow c $

Answer 1

Hint: We first find an equation for vector $\overrightarrow a $ then for vector $\overrightarrow b $ in terms of $\overrightarrow c $ and$\overrightarrow {PQ}$. Using these two equations and finding the sum of them we find the relation between vectors $\overrightarrow a $, $\overrightarrow b $ and$\overrightarrow c $. Since only the relation is asked the formula of the resultant is not necessary

Complete step by step answer:
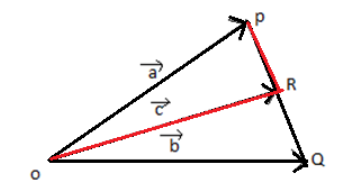
From the diagram we know that vector $\overrightarrow a $ can be written as sum of vector $\overrightarrow c $ and vector $\overrightarrow {PR} $
$\overrightarrow a = \overrightarrow c + \overrightarrow {PR} $

Vector $\overrightarrow b $ can be written as the sum of vector $\overrightarrow c $ and vector $\overrightarrow {RQ} $
$\overrightarrow b = \overrightarrow c + \overrightarrow {RQ} $

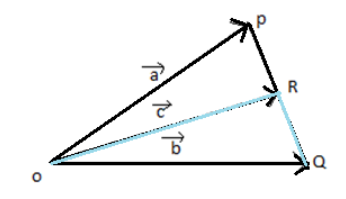
 Since the vectors $\overrightarrow {PR} $ and $\overrightarrow {RQ} $ are of equal magnitude and opposite in direction they can be equated as
$\overrightarrow {PR} $=$ - \overrightarrow {RQ} $
Adding vectors$\overrightarrow a $ and $\overrightarrow b $ using the equations formed
$ \overrightarrow a + \overrightarrow b = \overrightarrow c + \overrightarrow {PR} + \overrightarrow c + \overrightarrow {RQ} $
$ \because \overrightarrow {PR} = - \overrightarrow {RQ} $
  $\Rightarrow \overrightarrow a + \overrightarrow b = 2\overrightarrow c $

Hence option (A) $\overrightarrow a + \overrightarrow b = 2\overrightarrow c $ is the correct answer.

Additional information: This method is also called the parallelogram method of vector addition. A similar method called the triangle method can also be used to solve the problem. The parallelogram method states that the resultant vector of two different vectors represented in magnitude, direction, by the two adjacent sides of a parallelogram both of which are directed toward or away from their point of intersection is the diagonal of the parallelogram through that point. This diagonal is the resultant vector.

Note: We can also solve this problem by making two equations of vector $\overrightarrow c $ with respect to vector $\overrightarrow a $ and with vector$\overrightarrow b $. Adding these two equations we get $\overrightarrow {2c} $ on the left-hand side and $\overrightarrow a + \overrightarrow b = \overrightarrow {2c} $ on the right-hand side, giving us the same answer.