Question

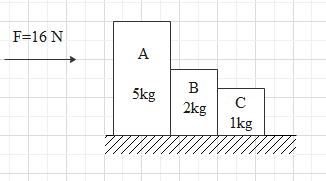
The given figure shows three blocks in contact and kept on a smooth horizontal surface. What is the ratio of force exerted by block A on B to that of B on C?

A.$3:1$
B. $1:3$
C. $2:3$
D. $3:2$

Answer 1

Hint: Look at this problem considering different systems, first consider all three blocks as a system, check the external forces and then apply Newton’s Second law, then follow the same for all three individual blocks or the two blocks from which you will obtain the required forces.

Complete step by step answer:
From the figure we can see
the mass of the block A, ${m_A} = 5\,kg$
mass of the block B, ${m_B} = 2\,kg$
mass of the block C, ${m_C} = 1\,kg$
Therefore, total mass of three blocks,
$M = {m_A} + {m_B} + {m_C}$
$ \Rightarrow M = 5\,kg + 2\,kg + 1\,kg$
$\therefore M = 8\,kg$
According to Newton 2nd law force is the rate of change of momentum. That is,
$F = \dfrac{{dP}}{{dt}}$
Where $P$ is a momentum given by
$P = mv$
Substituting this in equation 1 we get
$F = m\dfrac{{dv}}{{dt}}$
So, Newton's second law can also be expressed as
$F = ma$
Where, $m$ is the mass and $a$ is the acceleration.
From this acceleration is equal to
$a = \dfrac{F}{M}$
On substituting the given values, we get
Acceleration of the block
 $a = \,\dfrac{{16}}{8}\, = 2\,m/{s^2}$
Let ${F_{AB}}$ be the force of contact exerted by block A on B and let ${F_{BC}}$ be the force exerted by block B on C
So, we can write the net force on A as the force given on A minus contact force exerted by block A on B.
${m_A}a = F - {F_{AB}}$
That is,
$5 \times 2 = 16 - {F_{AB}}$
$ \Rightarrow {F_{AB}} = 6\,N$
Now, we can write the force on B as force on B due to A minus the force on C due to B.
${m_B}a = {F_{AB}} - {F_{CB}}$
That is,
$2 \times 2 = 6 - {F_{BC}}$
$ \Rightarrow {F_{BC}} = 2\,N$
Therefore,
The ratio of force exerted by block A on B to that of B on C is
$\dfrac{{{F_{AB}}}}{{{F_{BC}}}} = \dfrac{6}{2}$
$\therefore \dfrac{{{F_{AB}}}}{{{F_{BC}}}} = \dfrac{3}{1}$
So, the ratio of the two forces is 3:1 .
Thus, the answer is option A.

Note: The acceleration of the three blocks will be the same but net force on each block will be different due to the difference in mass of the blocks.
The contact force exerted by A on B is same as that of B on A. That is
${F_{AB}} = {F_{BA}}$
Also,
${F_{BC}} = {F_{CA}}$