Question

The potentiometer wire of length 100cm and resistance \[9\Omega \] is joined to a cell of e.m.f 10V and internal resistance \[1\Omega \] . Another cell of e.m.f 5Vand internal resistance \[2\Omega \] is connected and shown in Fig. The galvanometer G shows no deflection when the length AC is
                
(A) 52.52cm
(B) 53.56cm
(C) 54.2cm
(D) 55.55cm

Answer 1

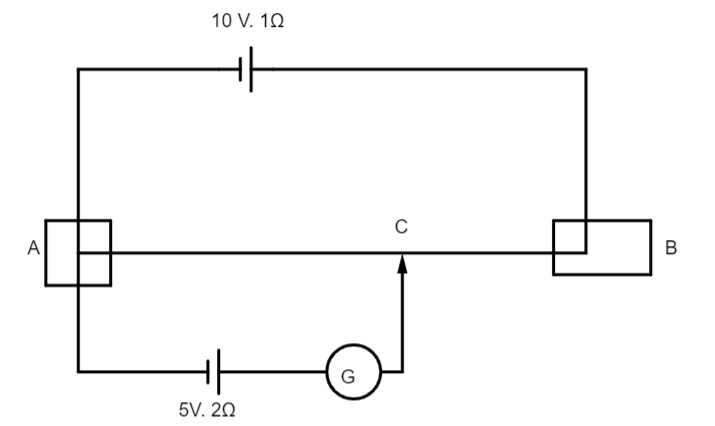
Hint: We will first see that galvanometer G shows no deflection so current is zero. We will find the potentiometer.
After that we will calculate the potential difference across the potentiometer wire. After that we will calculate the potential gradient i.e. potential per unit length.
Then we will find the length of AC using EMF i.e. \[m = Kl\] , where I=balancing length. After simplifying this equation, we will find the length of the AC wire.

Complete step by step solution
As the galvanometer G shows no deflection, we take current i.e. \[i = 0\] . Now after this we should find potential gradients.
To find potential gradients first we find current in the potentiometer. We know that \[i = \dfrac{v}{r}\] , where I is the current, v is the voltage and r is the resistance.
After putting the value of current and voltage we get:
 \[i = \dfrac{{10}}{{9 + 1}}\] , as given \[9\Omega \] is joined to a cell of E.M.F. 10V so, we have to add \[9\Omega \] resistance.
 \[i = 1\Omega \]
Now we calculate potential difference across potentiometer i.e. \[P.D = iR\]
 \[
  P.D = 1 \times 9 \\
  P.D = 9V \\
 \]
Now we calculate potential gradients. Potential gradient is the potential per unit length of the wire s. i.e. \[K = \dfrac{v}{l}\] , where \[{\text{l}}\] is the length of the wire.
 \[K = \dfrac{9}{{100}} \times 100\dfrac{v}{m} = 9\dfrac{v}{m}\] , here 100cm is converted into m.
EMF i.e. \[{\text{m = Kl}}\] , where \[{\text{l}}\]=balancing length.
 \[5 = Kl\] , where\[{\text{k}}\] \[ = 9\dfrac{v}{m}\]
 \[l = \dfrac{5}{9}m = \dfrac{5}{9} \times 100cm\]
 \[l = \dfrac{{500}}{9}cm = 55.55cm\]
AC=55.55cm.

So, the correct option is D

Note: Always remember to convert the S.I unit as required in the question as in this question we have to convert the length of the AC wire from’ m’ to ‘cm’.
Also note that when the potential across the potentiometer wire and the EMF applied are equal, at equal potentials then there is no flow of the current as there is no potential difference between two ends.
Also remember that the potentiometer works on the principle that when a constant current flows through a wire of uniform cross-sectional area, potential difference between its two points is directly proportional to the length of the wire between the two points.