
Three rays of light, namely red (R), green (G) and blue (B) are incident on the face PQ of a right angled prism PQR as shown in the figure.
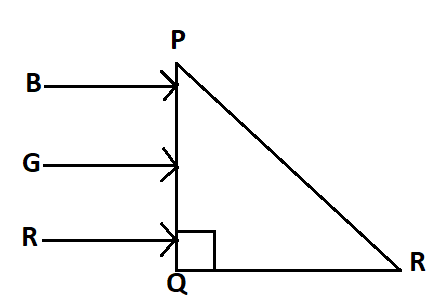
The refractive indices of the material of the prism for red, green and blue wavelengths are 1.27, 1.42 and 1.49 respectively. The colour of the ray(s) emerging out of the face PR is:
A. Blue
B. Green
C. Red
D. Blue and green
Answer
216.3k+ views
Hint:In optics critical angle is that angle of incidence at which the angle of refraction is \[{90^0}\]. The direction of light bends towards the normal if light enters a denser medium from a rarer medium. From Snell’s law, we can find a refractive index in the given medium.
Formula used:
The critical angle is given as:
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)\]
Where C is the critical angle
\[\mu {\rm{ is refractive index}}\]
Complete step by step solution:
Given the refractive index of the material of the prism for red colour,\[{\mu _R}\] =1.27
The refractive index of the material of the prism for green colour, \[{\mu _G}\] =1.42
The refractive index of the material of the prism for the blue colour, \[{\mu _B}\] =1.49
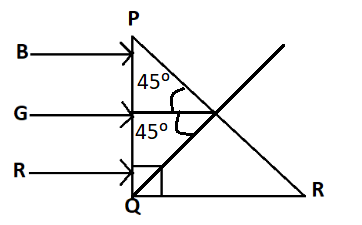
Image: In right angled triangle PQR, shows \[\angle PRQ = {45^0}\]
For Total Internal Reflection, at the face PR,
Incident angle, \[i = {45^0} = {\sin ^{ - 1}}\left( {\dfrac{1}{{\sqrt 2 }}} \right)\]
As critical angle is given as:
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)\]
If the rays which are not passing through the face PR, must follow the condition,
i > C or \[{45^0} > C\]
And if the rays which are pass through the face PR, must follow the condition,
i < C or \[{45^0} < C\]
For blue colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.49}}} \right)\]
\[\Rightarrow {\mu _B} = 1.49 > \mu = \sqrt 2 = 1.414\]
Thus it shows i > C, blue not passing through the face PR.
For green colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.42}}} \right)\]
\[\Rightarrow {\mu _G} = 1.42 > \mu = \sqrt 2 = 1.414\]
Thus it shows i > C, green not passing through the face PR.
For red colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.27}}} \right)\]
\[\Rightarrow {\mu _R} = 1.27 < \mu = \sqrt 2 = 1.414\]
Thus it shows i < C, red pass through the face PR.
Here μG and μB are more than μ.
∴ only red will come out.
Hence option C is the correct answer.
Note: The light is a form of energy that exhibits various phenomena like reflection, refraction, dispersion, total internal reflection(TIR). If the light rays pass from a denser medium to a less dense medium then this phenomenon is known as total internal reflection.
Formula used:
The critical angle is given as:
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)\]
Where C is the critical angle
\[\mu {\rm{ is refractive index}}\]
Complete step by step solution:
Given the refractive index of the material of the prism for red colour,\[{\mu _R}\] =1.27
The refractive index of the material of the prism for green colour, \[{\mu _G}\] =1.42
The refractive index of the material of the prism for the blue colour, \[{\mu _B}\] =1.49

Image: In right angled triangle PQR, shows \[\angle PRQ = {45^0}\]
For Total Internal Reflection, at the face PR,
Incident angle, \[i = {45^0} = {\sin ^{ - 1}}\left( {\dfrac{1}{{\sqrt 2 }}} \right)\]
As critical angle is given as:
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)\]
If the rays which are not passing through the face PR, must follow the condition,
i > C or \[{45^0} > C\]
And if the rays which are pass through the face PR, must follow the condition,
i < C or \[{45^0} < C\]
For blue colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.49}}} \right)\]
\[\Rightarrow {\mu _B} = 1.49 > \mu = \sqrt 2 = 1.414\]
Thus it shows i > C, blue not passing through the face PR.
For green colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.42}}} \right)\]
\[\Rightarrow {\mu _G} = 1.42 > \mu = \sqrt 2 = 1.414\]
Thus it shows i > C, green not passing through the face PR.
For red colour,
\[C = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.27}}} \right)\]
\[\Rightarrow {\mu _R} = 1.27 < \mu = \sqrt 2 = 1.414\]
Thus it shows i < C, red pass through the face PR.
Here μG and μB are more than μ.
∴ only red will come out.
Hence option C is the correct answer.
Note: The light is a form of energy that exhibits various phenomena like reflection, refraction, dispersion, total internal reflection(TIR). If the light rays pass from a denser medium to a less dense medium then this phenomenon is known as total internal reflection.
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Atomic Structure: Definition, Models, and Examples

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




