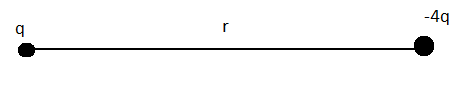Answer
110.7k+ views
Hint: Now, from the above problem, we know that two charges are placed at a distance $r$ from each other and it is also given that a third charge is also placed in such a way that the other two charges do not move if they are released. Now, we know that opposite charges attract each other. So, this third charge will be placed at a distance $x$ from the second charge. Now, by adding the force exerted by the third charge to first and second and equating it to zero, we will get our answer.
Formula used:
Force between the two charges placed at distance $d$ is \[F = \dfrac{{K \cdot {q_1} \cdot {q_2}}}{{{d^2}}}\] . Where, \[K\] is proportionality constant known as the Coulomb's law constant and ${q_1},{q_2}$ are the two charges.
Complete step by step solution:

Now, the third charge is $q'$and it is placed at a distance $x$ from the charge \[ - 4q\] .
Now, using the formula for force between the charge $q$ and $q'$ ,
We get,
\[F = \dfrac{{K \cdot q \cdot q'}}{{{{\left( {r + x} \right)}^2}}}\] ,
Now, using the same formula for force between the charge \[ - 4q\] and $q'$ ,
We get,
\[F = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( x \right)}^2}}}\]
Now, equating the adding the above two equations and equating them to 0 because we know that the system is in equilibrium.
We get,
\[\dfrac{{K \cdot q \cdot q'}}{{{{\left( {r + x} \right)}^2}}} + \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( x \right)}^2}}} = 0...........\left( 1 \right)\]
Now, simplifying the equation, we get,
\[
\dfrac{1}{{{{\left( {r + x} \right)}^2}}} + \dfrac{{ - 4}}{{{{\left( x \right)}^2}}} = 0 \\
{x^2} - 4{\left( {r + x} \right)^2} = 0 \\
{x^2} = 4{\left( {r + x} \right)^2} \\
\]
Now, taking square root on both sides, we get,
$
x = 2r + 2x \\
x = - 2r \\
$
Which means that the third charge is placed at a distance $2r$ from the charge \[ - 4q\] .
Now, taking the forces exerted on the second charge by first and third charge.
${F_{23}} = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( { - 2r} \right)}^2}}}$
${F_{13}} = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q}}{{{{\left( r \right)}^2}}}$
Now, subtracting the above equations and evaluating them to 0.
$\dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( { - 2r} \right)}^2}}} - \dfrac{{K \cdot \left( { - 4q} \right) \cdot q}}{{{{\left( r \right)}^2}}} = 0$
Now, simplifying the above equation,
$
\dfrac{{q'}}{{4{r^2}}} - \dfrac{q}{{{r^2}}} = 0 \\
q' = 4q \\
$
Now, the value of the third charge is $4q$ .
Hence, the correct option is D.
Note: In the given problem the system of the three charges are in equilibrium. So, the resultant force exerted on the one charge by the other two is equal to zero. So, we have calculated the force on the second charge by the other two charges to calculate the value of the third charge.
Formula used:
Force between the two charges placed at distance $d$ is \[F = \dfrac{{K \cdot {q_1} \cdot {q_2}}}{{{d^2}}}\] . Where, \[K\] is proportionality constant known as the Coulomb's law constant and ${q_1},{q_2}$ are the two charges.
Complete step by step solution:

Now, the third charge is $q'$and it is placed at a distance $x$ from the charge \[ - 4q\] .
Now, using the formula for force between the charge $q$ and $q'$ ,
We get,
\[F = \dfrac{{K \cdot q \cdot q'}}{{{{\left( {r + x} \right)}^2}}}\] ,
Now, using the same formula for force between the charge \[ - 4q\] and $q'$ ,
We get,
\[F = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( x \right)}^2}}}\]
Now, equating the adding the above two equations and equating them to 0 because we know that the system is in equilibrium.
We get,
\[\dfrac{{K \cdot q \cdot q'}}{{{{\left( {r + x} \right)}^2}}} + \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( x \right)}^2}}} = 0...........\left( 1 \right)\]
Now, simplifying the equation, we get,
\[
\dfrac{1}{{{{\left( {r + x} \right)}^2}}} + \dfrac{{ - 4}}{{{{\left( x \right)}^2}}} = 0 \\
{x^2} - 4{\left( {r + x} \right)^2} = 0 \\
{x^2} = 4{\left( {r + x} \right)^2} \\
\]
Now, taking square root on both sides, we get,
$
x = 2r + 2x \\
x = - 2r \\
$
Which means that the third charge is placed at a distance $2r$ from the charge \[ - 4q\] .
Now, taking the forces exerted on the second charge by first and third charge.
${F_{23}} = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( { - 2r} \right)}^2}}}$
${F_{13}} = \dfrac{{K \cdot \left( { - 4q} \right) \cdot q}}{{{{\left( r \right)}^2}}}$
Now, subtracting the above equations and evaluating them to 0.
$\dfrac{{K \cdot \left( { - 4q} \right) \cdot q'}}{{{{\left( { - 2r} \right)}^2}}} - \dfrac{{K \cdot \left( { - 4q} \right) \cdot q}}{{{{\left( r \right)}^2}}} = 0$
Now, simplifying the above equation,
$
\dfrac{{q'}}{{4{r^2}}} - \dfrac{q}{{{r^2}}} = 0 \\
q' = 4q \\
$
Now, the value of the third charge is $4q$ .
Hence, the correct option is D.
Note: In the given problem the system of the three charges are in equilibrium. So, the resultant force exerted on the one charge by the other two is equal to zero. So, we have calculated the force on the second charge by the other two charges to calculate the value of the third charge.
Recently Updated Pages
Write an article on the need and importance of sports class 10 english JEE_Main

Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

If x2 hx 21 0x2 3hx + 35 0h 0 has a common root then class 10 maths JEE_Main

The radius of a sector is 12 cm and the angle is 120circ class 10 maths JEE_Main

For what value of x function fleft x right x4 4x3 + class 10 maths JEE_Main

Other Pages
Electric field due to uniformly charged sphere class 12 physics JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

In Searles apparatus when the experimental wire is class 11 physics JEE_Main

The energy stored is a condenser is in the form of class 12 physics JEE_Main

Excluding stoppages the speed of a bus is 54 kmph and class 11 maths JEE_Main