Question

Variables x and y are such that, when $\ln y$ is plotted on the vertical axis and $\ln x$ is plotted on the horizontal axis, a straight line graph passing through the points $\left( {2.5,7.7} \right)$ and \[\left( {3.7,5.3} \right)\] is obtained.
A) Find the value of $\ln y$ when $\ln x$ is 0.

Answer 1

Hint: Plot the graph of the given $\ln x$ and $\ln y$ using given coordinates.
Find the slope of the straight line formed by using a two-point formula.
In the Cartesian plane, the horizontal line is the x-axis, and the vertical line is the y-axis. The x-axis and y-axis are perpendicular to each other.
The point where the x-axis and y-axis cut each other is called the origin, $\left( {0,0} \right)$ .
The coordinates of a point of the Cartesian plane is written in the form $\left( {x,y} \right)$.
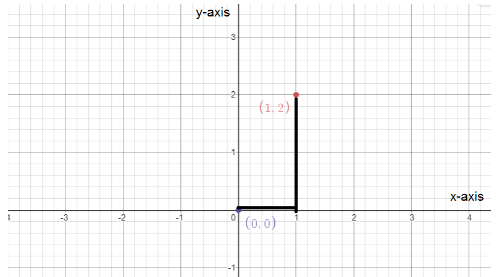
To plot coordinates $\left( {1,2} \right)$ on the Cartesian plane, from the origin $\left( {0,0} \right)$ go to its right side horizontally and mark 1 unit on the x-axis, and form 1 go upward up-to 2 units parallel to the y-axis.


Complete step-by-step answer:
Step 1: Plot the given coordinates
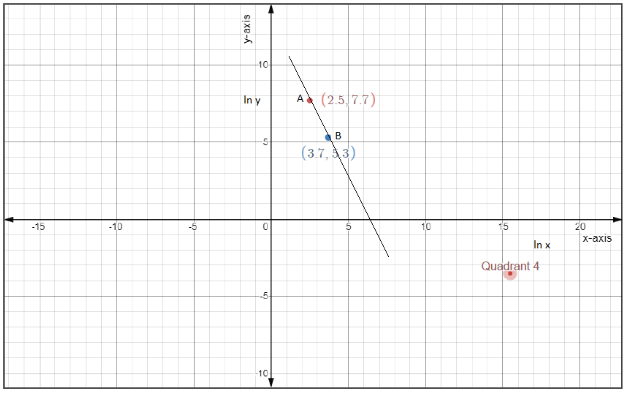
The points $A\left( {2.5,7.7} \right)$ and \[B\left( {3.7,5.3} \right)\]
Given that the x-axis is denoted by $\ln x$ and the y-axis is denoted by $\ln y$.

Step 2: Find the slope of the given straight line
The slope of a line is the tangent of the angle between the straight line and the positive direction of the x-axis. The slope is denoted by $m$.

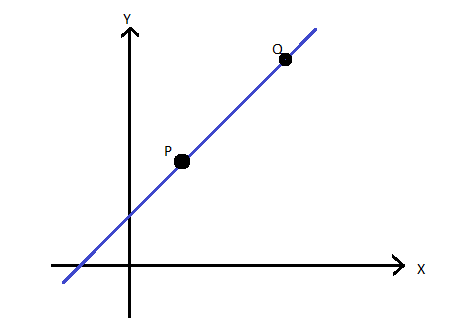
Let coordinate of point \[P\left( {{x_1},{y_1}} \right)\] and \[Q\left( {{x_2},{y_2}} \right)\]
The slope of a line when coordinates of any two points on the line are given by:
Slope, $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
The slope of the given straight line with coordinates $A\left( {2.5,7.7} \right)$ and \[B\left( {3.7,5.3} \right)\] as \[A\left( {{x_1},{y_1}} \right)\] and \[B\left( {{x_2},{y_2}} \right)\] respectively.
Therefore, slope $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{5.3 - 7.7}}{{3.7 - 2.5}}$
$
  m = \dfrac{{ - 2.4}}{{1.2}} \\
  \because m = - 2 \\
 $
Step 3: Solve (a)
The slope of the given line is -2, no matter which on lines are used to calculate, the slope will be the same.
Let the value of $\ln y$is t when $\ln x$ is 0.
Thus the slope of the given straight line with coordinates $A\left( {2.5,7.7} \right)$ and \[C\left( {0,t} \right)\] as \[A\left( {{x_1},{y_1}} \right)\] and \[C\left( {{x_2},{y_2}} \right)\] respectively.
Therefore, slope $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{t - 7.7}}{{0 - 2.5}}$
$
   \Rightarrow - 2 = \dfrac{{t - 7.7}}{{ - 2.5}} \\
   \Rightarrow t - 7.7 = \left( { - 2} \right)\left( { - 2.5} \right) = 5 \\
   \Rightarrow t = 5 + 7.7 \\
  \because t = 12.7 \\
 $
Hence, $\ln y$= 12.7

Final answer: The value of $\ln y$ is 12.7 when $\ln x$ is 0.

Note: The value of $\ln y$can also be found by using the equation of the straight line.
The equation of a straight line with the slope, $m$of line and a point \[\left( {{x_1},{y_1}} \right)\]on the line, is given by:
\[\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)\]
The slope of the given straight line as calculated in step 2, is -2
$\because m = - 2$
Thus the equation of the given straight line with coordinates $A\left( {2.5,7.7} \right)$ as a point \[\left( {{x_1},{y_1}} \right)\] on the line is given by:
\[
  \left( {y - 7.7} \right) = - 2\left( {x - 2.5} \right) \\
   \Rightarrow y - 7.7 = - 2x + 5 \\
   \Rightarrow y + 2x - 12.7 = 0 \\
 \]
Let the value of $\ln y$is t when $\ln x$ is 0. Thus, the coordinates $\left( {0,t} \right)$ lie on the given straight line as well, therefore it will satisfy the equation of the line.
Thus \[y + 2x - 12.7 = 0\] at $\left( {0,t} \right)$
\[
  t + 2\left( 0 \right) - 12.7 = 0 \\
  \because t = 12.7 \\
 \]
Hence, $\ln y$= 12.7
The x-axis and y-axis divide the Cartesian plane into four parts, each part is known as a quadrant.
Pictorial representation of quadrants: