Equal Intercept Theorem: Brief Introduction
The is a fundamental tool of Euclidean Geometry. The concept of parellel lines and transversal is of great importance in our day-to-day life. And, the Equal intercept theorem extends our understanding of parallel lines and transversal and we can apply these concepts in our day-to-day life. In this article, we will see detailed proof of the theorem and the converse of the equal intercept theorem. We will solve some examples based on the concept of the theorem to strengthen our concepts and their application.
History of Mathematician
Euclid
Name: Euclid
Born: 325 BC
Died: 265 BC
Field: Mathematics
Nationality: Egypt
Statement of Equal Intercept Theorem
Equal Intercept Theorem states that if equal intercepts are made on three or more parallel lines by a transversal, then the intercept made by any other line on these lines will also be equal.
Equal Intercept Theorem Proof
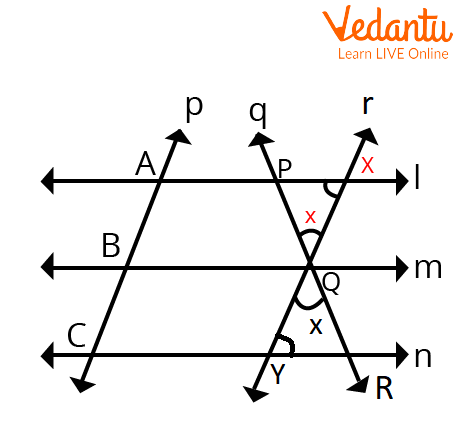
Proof of Equal Intercept Theorem
Given: Lines $l, m$, and $n$ such that $l\parallel m\parallel n, p$ is a transversal that cuts $l, m, n$ at $A, B, C$, respectively, such that $A B=B C$. Also, $\mathrm{q}$ is another transversal.
To Prove: $P Q=Q R$
Construction: Through $\mathrm{Q}, \mathrm{draw}$ a line $r$ such that $r \parallel$ $p$
Proof:
By construction, the pair of opposite sides are parallel.
Opposite sides of the parallelogram are equal.
We have,
$r \parallel p$
As the pair of opposite sides are parallel.
Therefore, $A B Q X$ is a parallelogram.
$A B=X Q \quad \ldots$ (i) (Opposite sides of a parallelogram)
$B C=Q Y \quad \ldots$ (ii) (Given)
Given $A B=B C$ And $X Q=Q Y \ldots$ (3) $[$ From $(i)$ and $(i i)]$
Now, in $\triangle P Q X$ and $\triangle R Q Y$,
$\angle P Q X=\angle R Q Y$ Vertically opposite angles
$X Q=Q Y \quad[$ From (iii)]
$\angle P Q X=\angle R Y Q \quad$ (Alternate angles, $l \| n$, )
Therefore, by ASA congruence,
$\triangle P Q X$ and $\triangle R Q Y$ are congruent.
So, By CPCT, we can conclude that $P Q=Q R$.
Hence proved.
Limitations of Equal Intercept Theorem
The equal intercept theorem is applicable only in the case of parallel lines.
Applications of Equal Intercept Theorem
The equal Intercept Theorem is used to find the ratio of intercepts made by other lines on the parallel lines.
It is used in understanding the concept of the midpoint theorem.
The equal intercept theorem is used to derive the concept of the Basic Proportionality theorem which is limited to the case of two parallel lines.
Solved Examples
1. In the triangle $A B C, D E \parallel B C$, then find the value of $EC$?
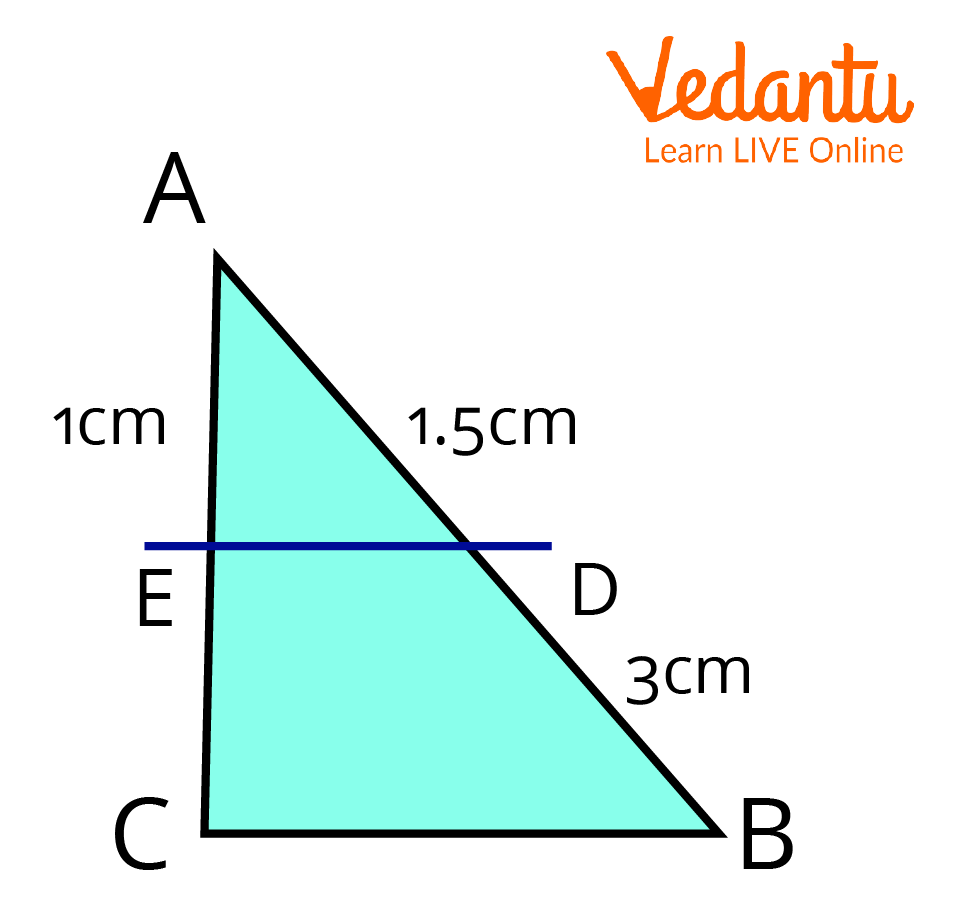
To find the value of EC
Ans:
Given, $D E \parallel B C$.
According to the basic proportionality theorem, a line drawn parallel to one side divides the other sides in an equal ratio.
So, $\dfrac{A D}{D B}=\dfrac{A E}{E C}$
$\Rightarrow \dfrac{1.5}{3}=\dfrac{1}{E C}$
$\Rightarrow \dfrac{1}{2}=\dfrac{1}{E C}$
$\Rightarrow E C=2$
Hence, the value of $E C$ is $2 \mathrm{~cm}$.
2. In the triangle $A B C, D E \parallel B C$, then find the value of $AD$?
In triangle ABC, we need to find AD
Ans:
Given, $D E \parallel B C$.
According to the basic proportionality theorem, a line drawn parallel to one side divides the other sides in an equal ratio.
So, $\dfrac{A D}{D B}=\dfrac{A E}{E C}$
$\Rightarrow \dfrac{A D}{5}=\dfrac{3}{7.5}$
$\Rightarrow \dfrac{A D}{1}=\dfrac{15}{7.5}$
$\Rightarrow A D=2$
Hence, the value of $A D$ is $2 \mathrm{~cm}$.
3. In $\triangle A B C, D$ is the midpoint of $A B$ and $E$ is the midpoint of $B C$.
Calculate $D E$, if $A C=8.6 \mathrm{~cm}$.
In a triangle ABC, D and E are midpoints of AB and BC.
Ans:
In $\triangle A B C, D$ and $E$ are the mid-points of $A B$ and $B C$, respectively.
Hence, by mid-point theorem, $DE \parallel A C$
and
$D E=\dfrac{1}{2} A C$
$D E=\dfrac{1}{2} A C=\dfrac{1}{2} \times 8.6$
We get
$DE = 4.3 \mathrm{~cm}$
Important Points to Remember
The intercept made by a transversal on three or more parallel lines is equal to the intercept made by other transversals.
The equal intercept theorem is a generalized version of Thales's Theorem.
Parallel Lines: If the distance between the lines is equal, then the lines are parallel.
Conclusion
In the above article, we have discussed the Equal Intercept Theorem and its proof followed by the converse of the equal intercept theorem. We have also discussed the applications of the theorem. So, we can conclude that Equal Intercept Theorem is a fundamental tool of Geometry and is based on applications of parallel lines and transversal and reduces our computational work based on its application as we have seen in the examples based on the theorem.
FAQs on Equal Intercept Theorem in Geometry
1. How is the equal intercept theorem different from the basic proportionality theorem?
The equal intercept theorem and basic proportionality theorem are both concerned with the parallel lines intersected by a transversal. But, both theorems are different from each other. The equal intercept theorem is more generalised compared to The basic Proportionality Theorem. The basic proportionality theorem also known as Thales's Theorem is applicable in the case of triangles, i.e., if a line is drawn parallel to one of the sides of the triangle, then the lines divide the other two sides of the triangle in equal proportion. On the other hand, the Equal intercept theorem is applicable in the case of any number of parallel lines intersected by any number of transversals.
2. What are parallel and transversal lines?
We can cross different types of lines in Geometry. The most important being Parallel and Transversal lines. The type of lines that never intersect each other are known as parallel lines. For example, the railway tracks, the stairs, etc., are the best real-life examples of parallel lines. On the other hand, Transversal Lines are the lines that intersect two or more distinct lines at two or more distinct points. And if the transversal line intersects two or more parallel lines, then that case would be of great significance.
3. Write some properties of Transversal Lines.
If a transversal line is formed when the line intersects two or more parallel lines, then there are numerous properties of such lines. Some of them can be stated as follows:
The pair of corresponding angles formed by a transversal with parallel lines are equal.
Conversely, if a pair of corresponding angles found between two lines intersected by a transversal are equal, then the lines are parallel.
The pair of alternate opposite interior and exterior angles are equal and interior angles on the same side are supplementary.
