Prime Factorization of 180

In this article, we will explore the factors of 180, pair factors, and the prime factorisation of 180, as well as solve examples for better understanding.

To get the pair factor of 180, multiply the two numbers in a pair to obtain the original number, which is 180. A factor of 180 will divide it equally. Those factors cannot be of a fractional or decimal value. 180 has a total of 12 factors. The factors are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. The sum of all factors of 180 is 546.

What are the Factors of 180?

Factors of 180 are the numbers that divide 180 exactly with no remainder. Since the number 180 is even composite, it has many factors other than 1 and 180. As a result, the factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180.

How to Find the Factors of 180?

The factors of 180 are the numbers that divide 180 exactly without the remainder. Therefore, the method for identifying and listing all of the factors of 180 is to count every integer from 1 to 180 and determine which values have an even quotient (which means no decimal place).

Here are all the factors for 180:

\[180\text{ }\div \text{ }1\text{ }=\text{ }180\]

1 is a factor of 180.

\[180\div 2=90\]

2 is a factor of 180.

\[180\text{ }\div \text{ }3\text{ }=\text{ }60\]

3 is a factor of 180.

\[180\text{ }\div \text{ }4\text{ }=\text{ }45\]

4 is a factor of 180.

\[180\text{ }\div \text{ }5\text{ }=\text{ }36\]

5 is a factor of 180.

\[180\text{ }\div \text{ }6\text{ }=\text{ }30\]

6 is a factor of 180.

\[180\text{ }\div \text{ }9\text{ }=\text{ }20\]

9 is a factor of 180.

\[180\text{ }\div \text{ }10\text{ }=\text{ }18\]

10 is a factor of 180.

\[180\text{ }\div \text{ }12\text{ }=\text{ }15\]

12 is a factor of 180.

\[180\text{ }\div \text{ }15\text{ }=\text{ }12\]

15 is a factor of 180.

\[180\text{ }\div \text{ }18\text{ }=\text{ }10\]

18 is a factor of 180.

\[180\text{ }\div \text{ }20\text{ }=\text{ }9\]

20 is a factor of 180.

\[180\text{ }\div \text{ }30\text{ }=\text{ }6\]

30 is a factor of 180.

\[180\text{ }\div \text{ }36\text{ }=\text{ }5\]

36 is a factor of 180.

\[180\text{ }\div \text{ }45\text{ }=\text{ }4\]

45 is a factor of 180.

\[180\text{ }\div \text{ }60\text{ }=\text{ }3\]

60 is a factor of 180.

\[180\text{ }\div \text{ }90\text{ }=\text{ }2\]

90 is a factor of 180.

\[180\text{ }\div \text{ }180\text{ }=\text{ }1\]

180 is a factor of 180.

Thus, all the factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180.

What is the Prime Factorization of 180?

180 is a composite number that should have prime factors. Prime factorisation of 180 refers to determining the prime factors of 180. Divide 180 by the smallest prime number possible to get the prime factor of 180. Then, take the result and divide it by the lowest prime number. Continue this process until you get 1.

Step 1: Divide 180 by the lowest prime number, i.e., 2

\[180\text{ }\div \text{ }2\text{ }=\text{ }90\]

Step 2: Again divide 90 by 2;

\[90\text{ }\div \text{ }2\text{ }=\text{ }45\]

So 2 can’t be a factor of 45, so go to the next prime number, i.e., 3.

Step 3: Divide 45 by 3;

\[45\div 3=15\]

Step 4: Divide 15 by 3;

\[15\text{ }\div \text{ }3\text{ }=\text{ }5\]

Step 5: Divide 5 by 5;

\[5\text{ }\div \text{ }5\text{ }=\text{ }1\]

Thus, we get 1 at the end of this division method, and we can’t go on with the division approach. Hence, the prime factorisation of 180 is \[2\text{ }\times \text{ }2\text{ }\times \text{ }3\text{ }\times \text{ }3\text{ }\times \text{ }5\] or \[{{2}^{2}}\times \text{ }{{3}^{2}}\times \text{ }5\] where 2, 3, and 5 are prime numbers.

Factor Tree of 180

Factor trees represent the factors of a number, especially its prime factorisation. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops.

We should also remember that 1 is not a prime number; thus, it will not appear in any factor tree.

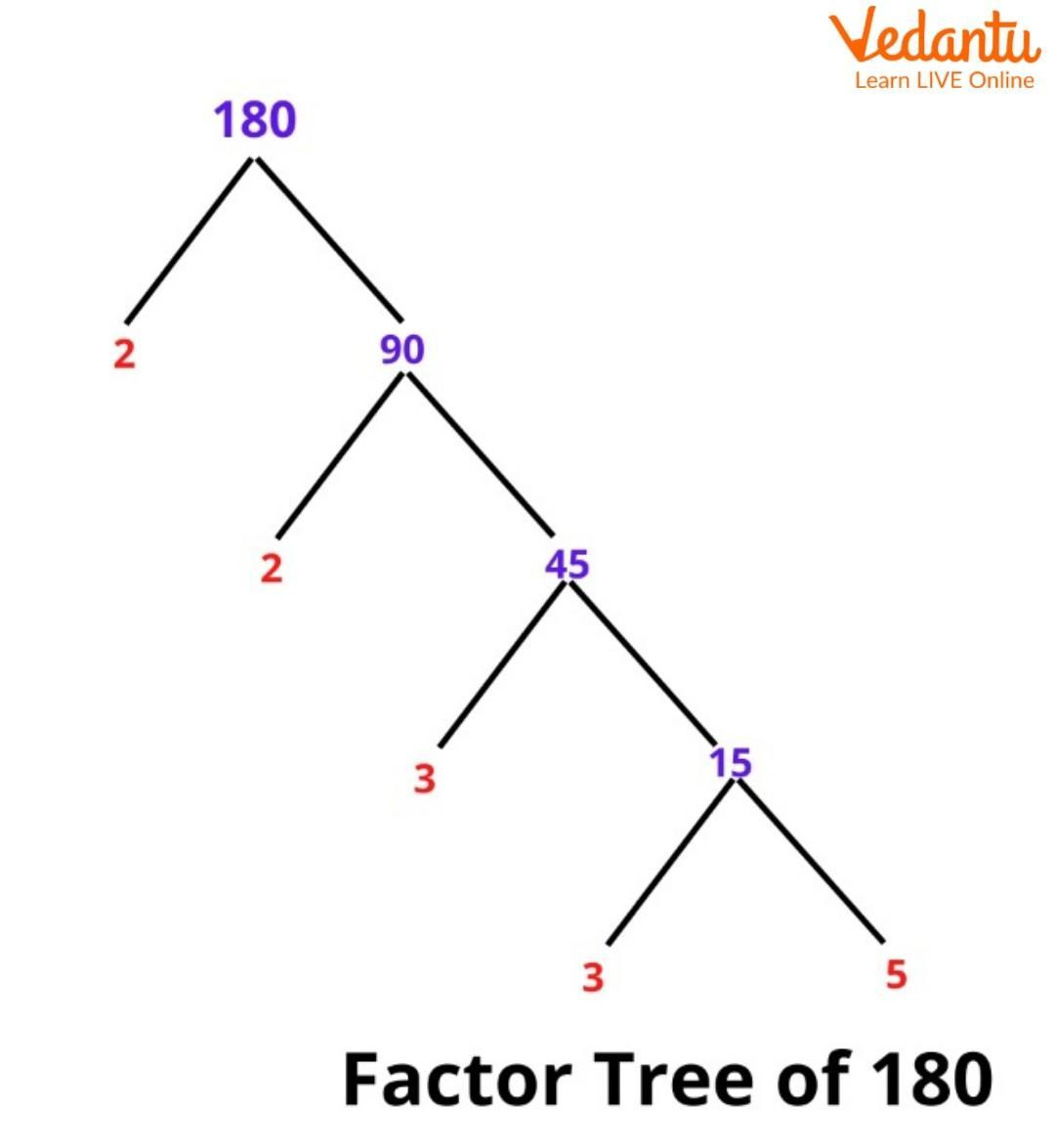
Factor Tree of 180

Negative Factors of a Number

A number's factors include all of the numbers that can be multiplied by one another to get that number. A negative number always contains one negative element. As a result, when we multiply two negative numbers then eventually we end up getting a positive number as a product. Here the negative factors of 180 are -1, -2, -3, -4, -5, -6, -9, -10, -12, -15, -18, -20, -30, -36, -45, -60, -90 and \[-180\].

Sum of Factors of 180

To get the sum of factors of a number, we have to add all the factors of that number. Here, all factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. So, the sum of factors of 180 is 1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 12 + 15 + 18 + 20 + 30 + 36 + 45 + 60 + 90 + 180 = 546.

Pair Factors of 180

When multiplied in pairs, the numbers that provide the original number, i.e. 180 are known as 180's pair factors. The pair factors of 180 might have both positive and negative values.

Thus, the positive pair factors are \[\left( 1,\text{ }180 \right),\text{ }\left( 2,\text{ }90 \right),\text{ }\left( 3,\text{ }60 \right),\text{ }\left( 4,\text{ }45 \right),\text{ }\left( 5,\text{ }36 \right),\text{ }\left( 6,\text{ }30 \right),\text{ }\left( 9,\text{ }20 \right),\text{ }\left( 10,\text{ }18 \right)\] and \[\left( 12,\text{ }15 \right)\].

Thus, the negative pair factors are \[\left( -1,\text{ }-180 \right),\text{ }\left( -2,\text{ }-90 \right),\text{ }\left( -3,\text{ }-60 \right),\text{ }\left( -4,\text{ }-45 \right),\text{ }\left( -5,\text{ }-36 \right),\text{ }\left( -6,\text{ }-30 \right),\text{ }\left( -9,\text{ }-20 \right),\text{ }\left( -10,\text{ }-18 \right)\] and \[\left( -12,\text{ }-15 \right)\].

Interesting Facts

• The pair factors of 180 might have both positive and negative values. For example, The pair factors of 180 might be \[(1,180)\] or \[(-1,-180)\]. When two negative numbers are multiplied, such as when \[-1\] and \[-180\] are multiplied, the answer is 180.

• 1 is the factor for each number, as 1 times a number is the number itself. Again, anything divided by 1 is the number itself.

Solved Examples

1. Write common factors of 150 and 180.

Ans: An integer that divides the original number into equal parts without a remainder is called a factor. Thus, we know that the factors of 150 and 180 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150 and 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180, respectively.

Thus, the common factors of 150 and 180 are 1, 2, 3, 5, 6, 10, 15 and 30.

2. Write all the factors of 13 and the prime factorization of 13.

Ans: The numbers that exactly divides 13 without leaving a remainder are known as the factors of 13. We know that the number 13 is divisible by 1 and 13. As a result, all of these integers are called the factors of 13.

13 is a prime number, which means it has only 2 factors. We know that the factors of 13 are 1 and 13. Thus, the prime factorization of 13 is \[1\times 13\].

3. Write negative pair factors of 180.

Ans: The pair factors of 180 might have both positive and negative values. For example, The pair factors of 180, might be \[(1,180)\] or \[(-1,-180)\]. Thus, the negative pair factors of 180 are (-1, -180), (-2, -90), (-3, -60), (-4, -45), (-5, -36), (-6, -30), (-9, -20), (-10, -18) and (-12, -15).

Practice Questions

1. How many positive pair factors does 180 have?

1. 7

2. 8

3. 9

4. 10

2. What is the sum of the factors of 180?

1. 540

2. 546

3. 246

4. 446

Answers:

1. C

2. B
   
   

Conclusion

Hence, the number 180 is even composite, it has many factors other than 1 and 180. The factors of 180 are the numbers that divide 180 exactly without the remainder. Thus, the factors are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. Thus, the prime factor of 180 is \[2\times 2\times 3\times 3\times 5\] or \[{{2}^{2}}\times {{3}^{2}}\times 5\] where 2, 3, and 5 are prime numbers.