




An Introduction to Menelaus Theorem
A statement regarding triangles in plane geometry is known as Menelaus's theorem, after Menelaus of Alexandria. It pertains to the collinearity of points on each of the three sides (stretched as necessary) of a triangle and is concerned with the relationships between the lengths of the segments on the sides of a triangle determined by an intersecting straight line. In this article, we will learn about Menelaus's theorem and the converse of Menelaus's theorem in detail. Let's begin by stating and proving the theorem.
History of Menelaus of Alexandria
Menelaus of Alexandria, a Greek mathematician and astronomer, was the first to identify geodesics on a curved surface as natural analogs of straight lines.
Even though very little is known about Menelaus's life, it is assumed that he resided in Rome, having likely relocated there after spending his formative years in Alexandria.

Menelaus of Alexandria (c. 70 – 140 CE)
Menelaus Theorem Statement
If line PQ intersects AB on triangle ABC, where P is on BC, Q is on the extension of AC, and R on the intersection of PQ and AB, then
\[\dfrac{{PB}}{{CP}}\cdot\dfrac{{QC}}{{QA}}\cdot\dfrac{{AR}}{{RB}} = 1\] (1)
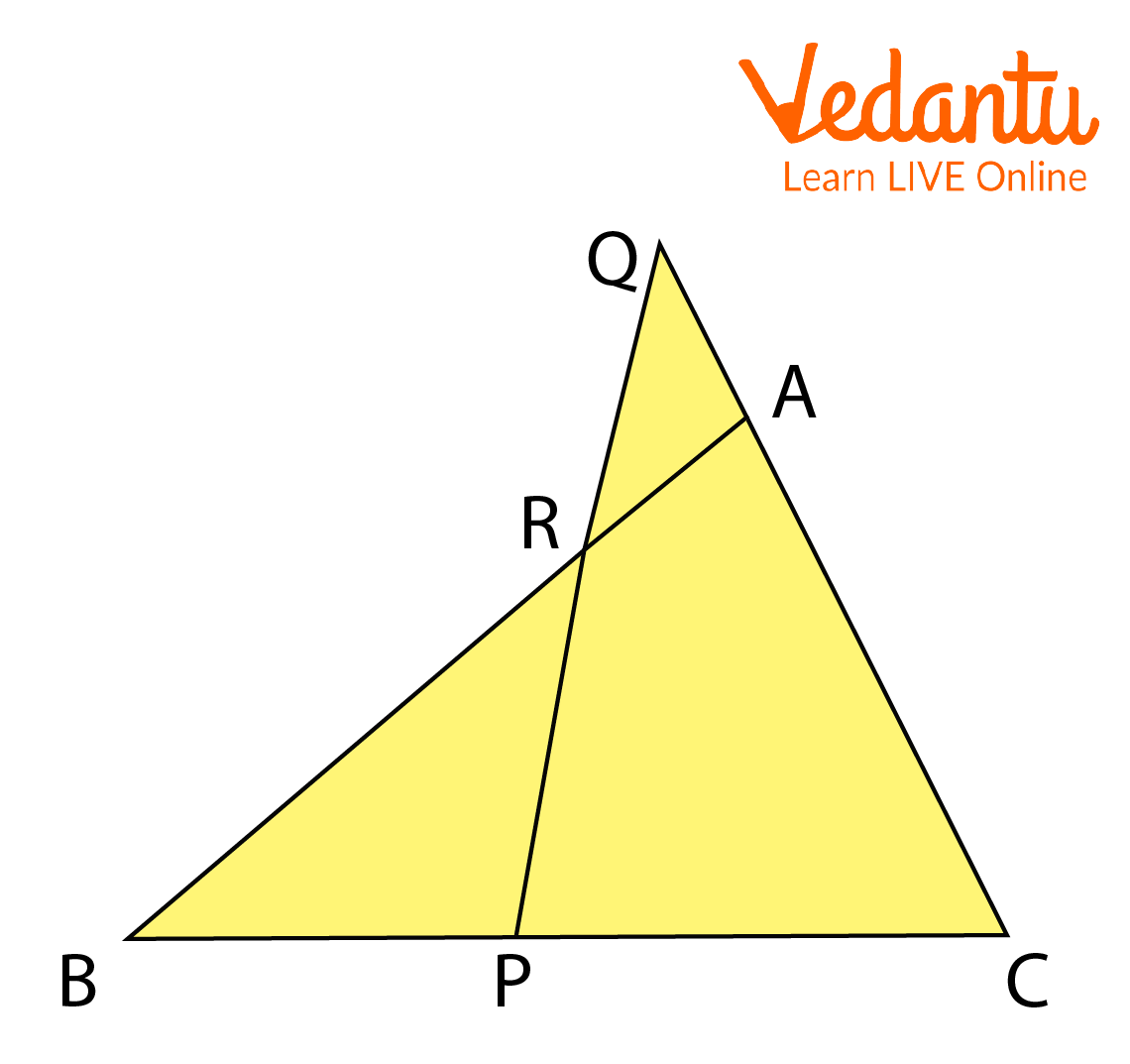
Menelaus Theorem
As an alternative, the theorem becomes clearer when expressed with directed segments,
\[BP\cdot CQ\cdot AR = CP\cdot QA\cdot RB\].
And equation (1) is referred to as the Menelaus theorem formula.
Menelaus Theorem Proof
Let's draw a line parallel to QP through point A to intersect BC at point K.
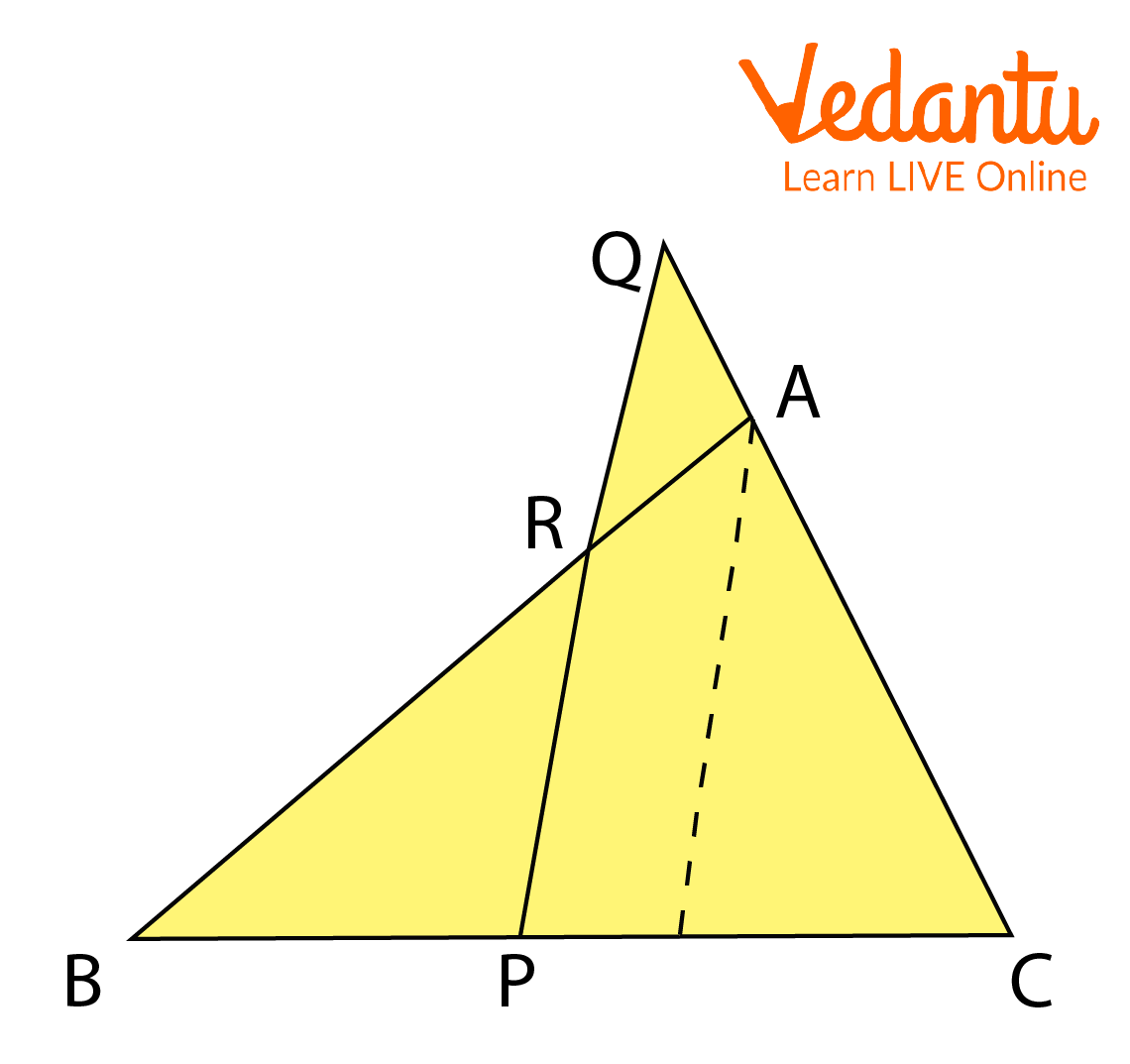
Menelaus Theorem Proof
\[\begin{array}{l} \triangle RBP\;\ \sim \; \triangle ABK\;\end{array}\]
\[ \Rightarrow \dfrac{{\;AR}}{{RB}}\; = \dfrac{{KP}}{{PB}}\]
\[\begin{array}{l} \triangle QCP\;\ \sim \; \triangle ACK\;\end{array}\]
\[\begin{array}{l}\\ \Rightarrow \dfrac{{QC}}{{QA}}\; = \dfrac{{\;CP}}{{KP}}\end{array}\]
To remove the PK element, multiply the two equalities to produce the following result:
\[\begin{array}{l}\dfrac{{AR}}{{RB}}\cdot\dfrac{{QC}}{{QA}} = \dfrac{{CP}}{{PB}}\\ \Rightarrow \dfrac{{AR}}{{RB}}\cdot\dfrac{{QC}}{{QA}}\cdot\dfrac{{PB}}{{CP}} = 1\end{array}\]
Hence proved.
The Converse of Menelaus Theorem
Menelaus' Theorem's converse is also true. If \[\dfrac{{BP}}{{PC}}\cdot\dfrac{{CQ}}{{QA}}\cdot\dfrac{{AR}}{{RB}} = 1\] in the below figure, then P, Q, and R are parallel. The converse can be used to demonstrate that three points are collinear.

Converse of Menelaus Theorem
Menelaus Theorem Applications
The Menelaus Theorem connects ratios obtained by cutting a triangle's sides.
The converse of the theorem, which states that three points on a triangle are only congruent if certain conditions are met, is also true and very effective in demonstrating that three points are congruent.
Menelaus Theorem Examples
1. In a triangle ABC, \[AB\; = AC\]. Internally, K and L of a transversal intersect AB and AC. It intersects BC produced at M. If \[KL\; = \;2LM\], find \[\dfrac{{KB}}{{LC}}\].

Triangle AKL
Ans: In triangle AKL, consider BCM as the transversal which intersects AK, AL, and KL at B, C, and M, respectively.
Therefore, By Melelaus’s theorem,
\[\begin{array}{l}\dfrac{{KB}}{{BA}}\cdot\dfrac{{\;AC}}{{CL}}\cdot\dfrac{{LM}}{{MK}}\; = - 1\\\dfrac{{KB}}{{CL}} \times \dfrac{1}{3}\; = \; - 1\left( {As\;KL\; = 2LM\; \Rightarrow KM\; = 3LM} \right)\\\dfrac{{KB}}{{CL}}\; = \; - 3\\ \Rightarrow \dfrac{{KB}}{{LC\;}}\; = \dfrac{{\;3}}{1}\end{array}\]
2. On the sides BC, CA, AB of triangle ABC points D, E, F are taken in such a way that \[\dfrac{{BD}}{{DC}} = \dfrac{{CE}}{{EA}} = \dfrac{{AF}}{{FB}} = \dfrac{2}{1}\]. Prove that area of the triangle determined by the lines AD, BE, and CF is \[\dfrac{1}{7}\] of the area of the ABC.
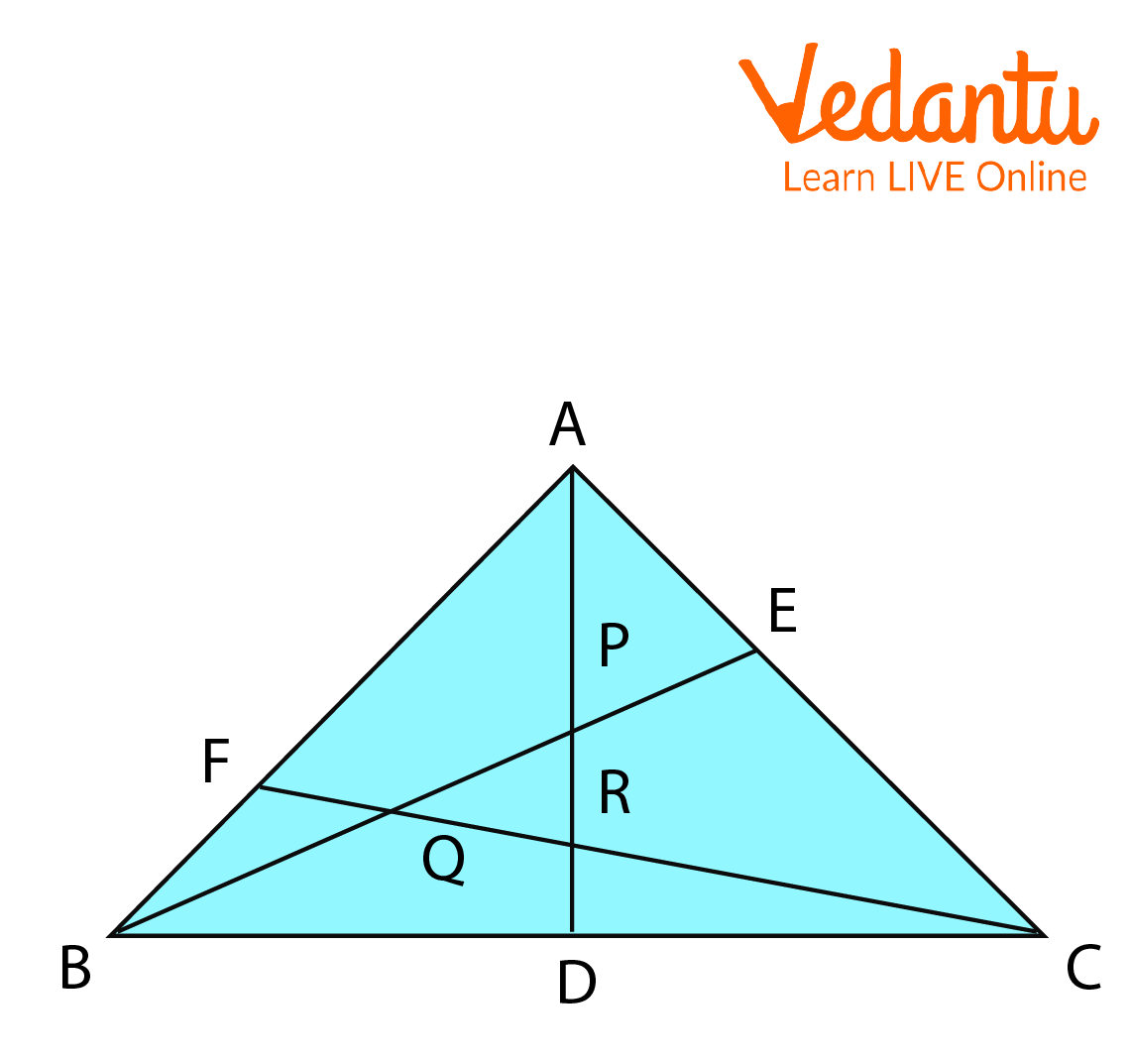
Proof of Area of the Triangle
Ans: Using Menelaus theorem in a triangle with the transversal CF,
$\dfrac{AR}{RD}\times\dfrac{1}{3}\times\dfrac{1}{2}=1\\$
$\Rightarrow\dfrac{RD}{AR}=\dfrac{1}{6}\\$
$\Rightarrow[ADC]=\dfrac{1}{3}[ABC]=\dfrac{1}{3}\triangle\\$
$\Rightarrow[ARC]=\dfrac{6}{7}[ADC]\\$
$\Rightarrow[ARC]=\dfrac{6}{7}\triangle$
3. In triangle ABC, let N be the midpoint of the median \[\overline {AM} \] and P be the point on the \[\overline {AC} \] such that \[\;AP\; = \dfrac{{\;1}}{3}AC\]. Prove that B, N, and P are collinear.
Ans: Lets first a figure using the provided information,
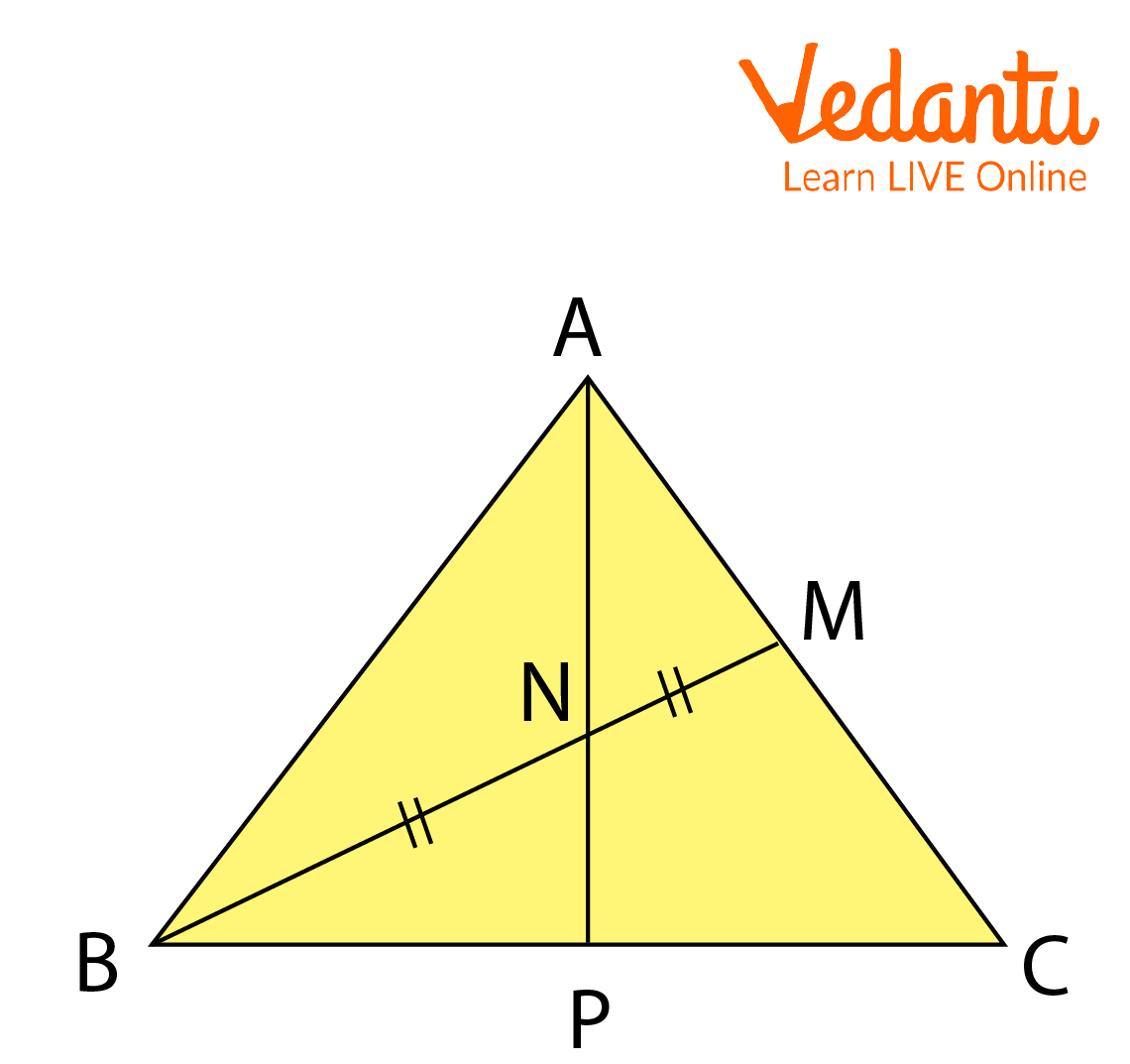
Triangle ABC
Consider the triangle AMC.
Point P is on AC, point B is on MC extended, and point N is on AM.
Now, by Menelaus’s theorem,
\[\begin{array}{l}\dfrac{{AN}}{{MN}}\cdot\dfrac{{MB}}{{BC}}\cdot\dfrac{{CP}}{{AP}}\; = 1\\1\cdot\dfrac{1}{2}\cdot\dfrac{2}{1}\; = 1\\1 = 1\end{array}\]
This is true.
So, B, N, and P are collinear.
Conclusion
In this article, we went over Menelaus’s theorem and its proof in detail. The converse of the theorem which also holds is also proved in the article. The article gives the idea that the Menelaus theorem is strong and has intriguing repercussions in several circumstances.
Important Points from the Theorem
The Menelaus Theorem connects ratios that can be found by cutting a triangle the sides.
In order to demonstrate that the three points are collinear.
The contrary of the theorem is likewise true and quite potent.
Important Formula/Results from the Theorem
The Menelaus Theorem predicts the following outcomes for a triangle ABC with a line PQ intersecting AB:
\[\dfrac{{PB}}{{CP}}\cdot\dfrac{{QC}}{{QA}}\cdot\dfrac{{AR}}{{RB}} = 1\]
FAQs on Menelaus Theorem
1. What is the transversal line?
We may have encountered various line types in geometry, like parallel, perpendicular, intersecting, and so on. In addition, we have another line that is referred to as a transversal. This occurs whenever a road crosses two or more other roads or when a railway line crosses numerous other lines. These provide an overview of a transversal. Establishing if two or more other lines in the Euclidean plane are parallel requires the use of transversals. This article will explain what a transversal line is and how it can make angles with both parallel and non-parallel lines using an example.
2. What are collinear points?
Collinear is a compound word made up of the Latin words "col" and "linear." "Col" denotes a group, and "Linear" denotes a line. As a result, collinear points are points that are connected to form a single line. There are numerous examples of collinearity in everyday life, like a row of students standing in a straight line, a group of apples arranged in a row next to one another, etc.
Geometrical terms like "collinear" and "many" refer to points that are on the same line. Collinear points are the group of points that lie along a single straight line.
3. Do Cova's theorem and Menelaus' theorem have any connections?
For a simple demonstration of their equivalency, Menelaus's theorem and Ceva's Theorem are identical. Menelaus' Theorem, as it is known. The Menelaus Theorem connects ratios that can be found by cutting a triangle in half. Ceva's theorem is essentially the reverse of this theorem and can be used to demonstrate that three lines are concurrent at a single point. The opposite of the theorem is also valid, and it is very effective in demonstrating that three points are collinear.


































