NCERT Solutions for Class 11 Maths Chapter 10 - In Hindi

प्रश्नावली 10.1 

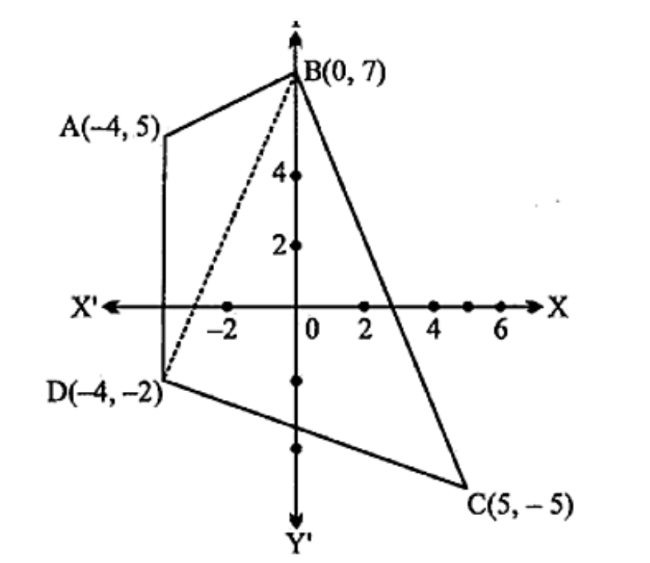
1. कारतीय तल मे एक त्रिभुज जिसके शीर्ष $( - 4,5),(0,7),(5, - 5),( - 4, - 2)$ है। इसका क्षेत्रफल भी ज्ञात कीजिए। 

उत्तर: दिया गया है कारतीय तल मे त्रिभुज के शीर्ष A,B,C,D जो $( - 4,5),(0,7),(5, - 5),( - 4, - 2)$ क्रमश है। 

यह चतुर्भुज ABCD को दो हिस्सों मे बाटा गया है, त्रिभुज ABC और त्रिभुज ABCD

ABCD का क्षेत्रफल = ABC का क्षेत्रफल + ACD का क्षेत्रफल 

हमे ज्ञात है की त्रिभुज का क्षेत्रफल = $\dfrac{{{1}}}{{{2}}}\mid {{{x}}_{{1}}}\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{3}}}} \right){{ + }}{{{x}}_{{2}}}\left( {{{{y}}_{{3}}}{{ - }}{{{y}}_{{1}}}} \right){{ + }}{{{x}}_{{3}}}\left( {{{{y}}_{{1}}}{{ - }}{{{y}}_{{2}}}} \right)\mid $

ABC का क्षेत्रफल = $\dfrac{1}{2}| - 4(7 + 5) + 0( - 5 - 5) + 5(5 - 7)|\;\; = \;\;\dfrac{1}{2}| - 4(12) + 0 + 5( - 2)|$

 = $\dfrac{1}{2}| - 48 + 0 - 10| = \dfrac{1}{2}| - 58|\; = \;\dfrac{{58}}{2}\; = \;29$ वर्ग इकाई 

ACD का क्षेत्रफल = $\dfrac{1}{2}| - 4( - 5 + 2) + 5( - 2 - 5) + ( - 4)(5 + 5)|\; = \;\dfrac{1}{2}| - 4( - 3) + 5( - 7) - 4(10)|$

 = $\dfrac{1}{2}|12 - 35 - 40|\; = \;\dfrac{1}{2}| - 63|\; = \;\dfrac{{63}}{2}$ वर्ग इकाई

ABCD का क्षेत्रफल = $\dfrac{{63}}{2} + 29\; = \;\dfrac{{121}}{2}$

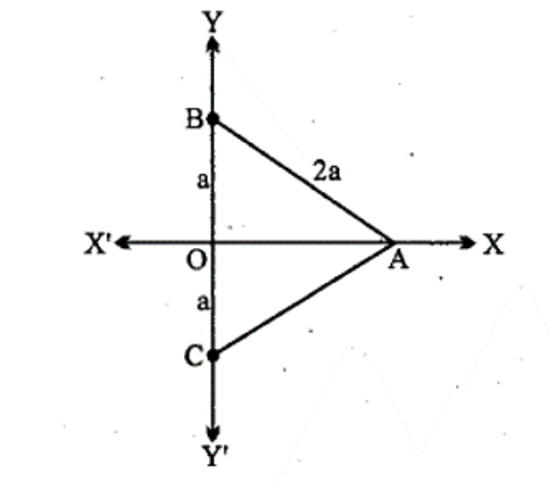
2. ${{2a}}$ भुजा के समबाहु त्रिभुज का आधार y- अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिन्दु मूल बिन्दु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए। 

उत्तर: मान लेते है त्रिभुज ABC मे BC y= अक्ष है और उसका मध्य बिन्दु मूल बिन्दु है। 

दिया गया है कि त्रिभुज ABC समबाहु है, 

AB = BC = CA =2a और OC = a (O मध्य बिन्दु है)

समकोण त्रिभुज OAC मे, ${{A}}{{{C}}^{{2}}}\;{{ = }}\;{{O}}{{{A}}^{{2}}}{{ + O}}{{{C}}^{{2}}}\; \Rightarrow \;{{{(2a)}}^{{2}}}\;{{ = }}\;{{{a}}^{{2}}}{{ + (OA}}{{{)}}^{{2}}}$

$\Rightarrow {{4}}{{{a}}^{{2}}}{{ - }}{{{a}}^{{2}}}{{ = (OA}}{{{)}}^{{2}}}$

$\Rightarrow {{OA = }}\sqrt {{{3}}{{{a}}^{{2}}}} {{ = }}\sqrt {{3}} {{a}}$

A के निर्देशांक होंगे ${{(}}\sqrt {{3}} {{a,0)}}$

अतः त्रिभुज ABC के निर्देशांक = ${{(}}\sqrt {{3}} {{a,0),(0,a),(0, - a)}}$

3. P${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ और Q${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$ के बीच की दूरी कीजिए जब 

(i) PQ, y – अक्ष के समांतर है 

उत्तर: दिया गया है P${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ और Q${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$

हमे ज्ञात हु कि जब कोई y- अक्ष के समांतर होती है तो ${{{x}}_{{1}}}\;{{ = }}\;{{{x}}_{{2}}}$

अतः PQ की दूरी = $\sqrt {{{\left( {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right)}^{{2}}}{{ + }}{{\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right)}^{{2}}}}$

= $\sqrt {{{0 + }}{{\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right)}^{{2}}}} \;{{ = }}\;\sqrt {{{\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right)}^{{2}}}} \;{{ = }}\;\left| {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right|$

(ii) PQ, y – अक्ष के समांतर है 

उत्तर: हमे ज्ञात हु कि जब कोई x- अक्ष के समांतर होती है तो ${{{y}}_{{1}}}\;{{ = }}\;{{{y}}_{{2}}}$

अतः PQ की दूरी = $\sqrt {{{\left( {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right)}^{{2}}}{{ + }}{{\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right)}^{{2}}}}$

= $\sqrt {{{0 + }}{{\left( {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right)}^{{2}}}} \;{{ = }}\;\sqrt {{{\left( {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right)}^{{2}}}} \;{{ = }}\;\left| {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right|$

4. x- अक्ष पर एक बिन्दु ज्ञात कीजिए जो $(7,6),(3,4)$ बिन्दुओ से समान दूरी पर है। 

उत्तर: मान लीते है कि P ${{(k,0)}}$ एक बिन्दु है जिसकी दूरी $(7,6),(3,4)$ के बराबर है। 

$\sqrt {{{{{(7 - k)}}}^{{2}}}{{ + (6 - 0}}{{{)}}^{{2}}}} {{ = }}\sqrt {{{{{(3 - k)}}}^{{2}}}{{ + (4 - 0}}{{{)}}^{{2}}}}$

$\Rightarrow \;{{{(7 - k)}}^{{2}}}{{ + (6 - 0}}{{{)}}^{{2}}}\;{{ = }}\;{{{(3 - k)}}^{{2}}}{{ + (4 - 0}}{{{)}}^{{2}}}$

$\Rightarrow \;{{49 + }}{{{k}}^{{2}}}{{ - 14k + 36}}\;{{ = }}\;{{9 + }}{{{k}}^{{2}}}{{ - 6k + 16}}$

$\Rightarrow  - 8{{k}}\; = \;25 - 85\; \Rightarrow \;{{k}}\; = \;\dfrac{{60}}{8}\; = \;\dfrac{{15}}{2}$

अतः P के निर्देशांक होंगे $(\dfrac{{15}}{2},0)$

5. रेखा की ढाल ज्ञात कीजिए जो मूल बिन्दु और P $(0,4)$ और B $(8,0)$ बिन्दुओ को मिलने वाले रेखाखण्ड के मध्य बिन्दु से जाती है। 

उत्तर: P $(0,4)$ और B $(8,0)$ बिन्दुओ को मिलने वाले रेखाखण्ड के मध्य बिन्दु के निर्देशांक होंगे 

${{x}}\;{{ = }}\;\dfrac{{{{(8 + 0)}}}}{{{2}}}\;{{ = }}\;{{4,y}}\;{{ = }}\;\dfrac{{{{0 - 4}}}}{{{2}}}\;{{ = }}\;{{ - 2}}$

P $(0,4)$ और B $(8,0)$ बिन्दुओ को मिलने वाले रेखाखण्ड के मध्य बिन्दु के निर्देशांक होंगे ${{(4, - 2)}}$

हमे ज्ञात है कि रेखाखण्ड ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ , ${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$ से बनने वाली रेखा की ढाल = $\dfrac{{{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}}}{{{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}}}$

रेखखण्ड ${{(4, - 2)}}$ और ${{(0,0)}}$ से बनने वाली रेखा की ढाल = $\dfrac{{ - 2 - 0}}{{4 - 0}}\; = \;\dfrac{{ - 1}}{2}$

6. पाइथागोरस प्रेमय के प्रयोग बिना दिखलाइए कि बिंदी $(4,4),(3,5),( - 1, - 1)$ एक समकोण त्रिभुज के शीर्ष है। 

उत्तर: दिया गया है $(4,4),(3,5),( - 1, - 1)$

AB की ढाल = $\dfrac{{{{5 - 4}}}}{{{{3 - 4}}}}\;{{ = }}\;{{ - 1}}\;{{ = }}\;{{{m}}_{{1}}}$

BC की ढाल = $\dfrac{{{{5 + 1}}}}{{{{3 + 1}}}}\;{{ = }}\;\dfrac{{{6}}}{{{4}}}\;{{ = }}\;\dfrac{{{3}}}{{{2}}}\;{{ = }}\;{{{m}}_{{2}}}$

CA की ढाल = $\dfrac{{{{4 + 1}}}}{{{{4 + 1}}}}\;{{ = }}\;{{1}}\;{{ = }}\;{{{m}}_{{3}}}$

यहा ${{{m}}_{{3}}}{{ \times }}{{{m}}_{{1}}}\;{{ = }}\;{{ - 1}}$ है 

अतः AB, BC के लम्बवत है A, B, C क्रमश $(4,4),(3,5),( - 1, - 1)$ एक समकोण त्रिभुज के शीर्ष है।

7. उस रेखा का समीकरण ज्ञात कीजिए जो y- अक्ष की धन दिशा से वामावर्त मापा गया $30^\circ$ का कोण बनती है। 

उत्तर: अगर एक रेखा y-अक्ष की धन दिशा से वामावर्त मापा गया $30^\circ$ का कोण बनती है तो x-अक्ष की धन दिशा से ${30^\circ } + {90^\circ }\; = \;{120^\circ }$ का कोण बनाएगी। 

अतः उस रेखा की ढाल = ${{tan12}}{{{0}}^{{^\circ }}}\;{{ = }}\;{{ - }}\sqrt {{3}}$

8. ${{x}}$ का वह मान ज्ञात कीजिए जिसके लिए बिन्दु $({{x}}, - 1),(2,1),(4,5)$ संरेख है। 

उत्तर: दिया गया है कि बिंदी A, B, C क्रमश $({{x}}, - 1),(2,1),(4,5)$ संरेख है।

AB की ढाल = BC की ढाल 

$\Rightarrow \;\dfrac{{{{1 + 1}}}}{{{{2 - x}}}}\;{{ = }}\;\dfrac{{{{5 - 1}}}}{{{{4 - 2}}}}$

$\Rightarrow \;2 - {{x}}\; = \;1$

$\Rightarrow \;{{x}}\; = \;1$

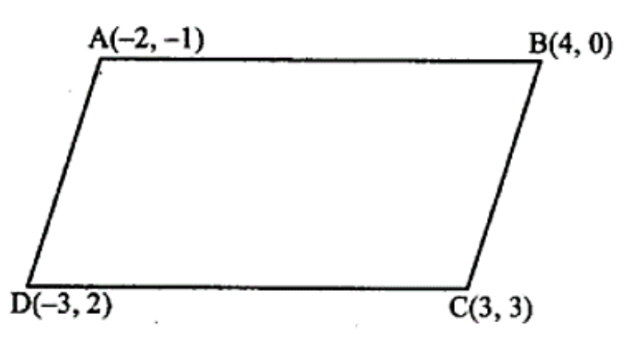
9. दूरी सूत्र के प्रयोग किए बिना दिखलाइए कि बिन्दु ${{( - 2, - 1),(4,0),(3,3),( - 3,2)}}$ एक समांतर चतुर्भुज के शीर्ष है। 

उत्तर: मान लेते है कि एक चतुर्भुज के शीर्ष A, B, C, D क्रमश ${{( - 2, - 1),(4,0),(3,3),( - 3,2)}}$ है 

AB की ढाल = $\dfrac{{0 + 1}}{{4 + 2}}\; = \;\dfrac{1}{6}$

BC की ढाल = $\dfrac{{3 - 0}}{{3 - 4}}\; = \; - 3$

CD की ढाल = $\dfrac{{2 - 3}}{{ - 3 - 3}}\; = \;\dfrac{1}{6}$

DA की ढाल = $\dfrac{{ - 1 - 2}}{{ - 2 + 3}}\; = \; - 3$

AB की ढाल = CD की ढाल 

BC की ढाल = DA की ढाल 

A, B, C, D एक समांतर त्रिभुज के शीर्ष है।

10. x- अक्ष और ${{(3, - 1),(4, - 2)}}$ बिन्दुओ को मिलने वाली रेखा के बीच के कोण ज्ञात कीजिए। 

उत्तर: A, B क्रमश ${{(3, - 1),(4, - 2)}}$ बिन्दुओ को मिलने वाली रेखा की ढाल = $\dfrac{{ - 2 + 1}}{{4 - 3}}\; = \; - 1$

मान लेते है कि अक्ष और के बीच का कोण $\theta$ है। 

$\tan \theta \; = \; - 1\;$

$\Rightarrow \;\theta \; = \;{180^\circ } - {45^\circ }\; = \;{35^\circ }$

11. एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है। यदि दोनों के बीच के कोण का स्पर्शज्या $\dfrac{1}{3}$ है तो रेखाओ की ढाल ज्ञात कीजिए। 

उत्तर: मान लेते है कि ${{{m}}_{{1}}}\;{{,}}\;{{{m}}_{{2}}}$ रेखाओ की ढाल है 

${{{m}}_{{1}}}\;{{ = }}\;{{2}}{{{m}}_{{2}}}$

दिया गया है कि ${{tan}}\theta \;{{ = }}\;\dfrac{1}{3}$

$\Rightarrow \;\dfrac{{{{{m}}_{{1}}}{{ - }}{{{m}}_{{2}}}}}{{{{1 + }}{{{m}}_{{1}}}{{{m}}_{{2}}}}}\; = \;\dfrac{1}{3} \Rightarrow \;\dfrac{{{{2}}{{{m}}_{{2}}}{{ - }}{{{m}}_{{2}}}}}{{{{1 + 2}}{{\left( {{{{m}}_{{2}}}} \right)}^{{2}}}}}\; = \;\dfrac{1}{3}\; \Rightarrow \;\dfrac{{{{{m}}_{{2}}}}}{{{{1 + 2}}{{\left( {{{{m}}_{{2}}}} \right)}^{{2}}}}}\; = \;\dfrac{1}{3}$

$\Rightarrow \;{{1 + 2}}{\left( {{{{m}}_{{2}}}} \right)^{{2}}}\;{{ = }}\;{{3}}{{{m}}_{{2}}}\; \Rightarrow \;\left( {{{{m}}_{{2}}}{{ - 1}}} \right)\left( {{{2}}{{{m}}_{{2}}}{{ - 1}}} \right)\;{{ = }}\;{{0}}$

$\Rightarrow \;{{{m}}_{{2}}}{{ = }}\dfrac{{{1}}}{{{2}}}{{ , }}{{{m}}_{{2}}}{{ = 1}}$

$\therefore {{{m}}_{{1}}}{{ = 1}}\;{{,}}\;{{{m}}_{{2}}}{{ = 2}}$

12. एक रेखा ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ और ${{(h,k)}}$ से जाती है। यदि रेखा की ढाल ${{m }}$ है तो दिखाइए कि ${{k - }}{{{y}}_{{1}}}{{ = m}}\left( {{{h - }}{{{x}}_{{1}}}} \right)$ 

उत्तर: दिया गया है कि रेखा ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ और ${{(h,k)}}$ से जाती है और उस रेखा की ढाल ${{m }}$ है

अतः उस रेखा की ढाल ${{m }}$ = $\dfrac{{{{k - }}{{{y}}_{{1}}}}}{{{{h - }}{{{x}}_{{1}}}}}$

$\Rightarrow \;\left( {{{k}} - {{{y}}_1}} \right)\; = \;{{m}}\left( {{{h}} - {{{x}}_1}} \right)$

13. यदि तीन बिन्दु $({{h}},0),({{h}},{{k}}),(0,{{k}})$ एक रेखा पर है तो दिखाइए की $\dfrac{{{a}}}{{{h}}}{{ + }}\dfrac{{{b}}}{{{k}}}{{ = 1}}$

उत्तर: दिया गया है कि बिन्दु A, B, C क्रमश $({{h}},0),({{h}},{{k}}),(0,{{k}})$ एक रेखा पर है। 

AB की ढाल = $\dfrac{{{{b - 0}}}}{{{{a - h}}}}\;{{ = }}\;\dfrac{{{b}}}{{{{a - h}}}}$

BC की ढाल = $\dfrac{{{{k - b}}}}{{{{0 - a}}}}\;{{ = }}\;\dfrac{{{{k - b}}}}{{{{ - a}}}}$

AB की ढाल = BC की ढाल

$\dfrac{{{b}}}{{{{a - h}}}}\;{{ = }}\;\dfrac{{{{k - b}}}}{{{{ - a}}}}\; \Rightarrow \;{{ - ab}}\;{{ = }}\;{{ak - ab - hk + hb}}$

$\Rightarrow \;{{ak + hb}}\;{{ = }}\;{{hk}}$

$\Rightarrow \;\dfrac{{{a}}}{{{h}}}{{ + }}\dfrac{{{b}}}{{{k}}}\;{{ = }}\;{{1}}$

14. जनसंख्या और वर्ष के निमनलिखित लेखाचित्र पर विचार कीजिए। रेखा AB की ढाल ज्ञात कीजिए और इसके प्रयोग से बताइए कि वर्ष 2010 मे जनसंख्या कितनी होगी?

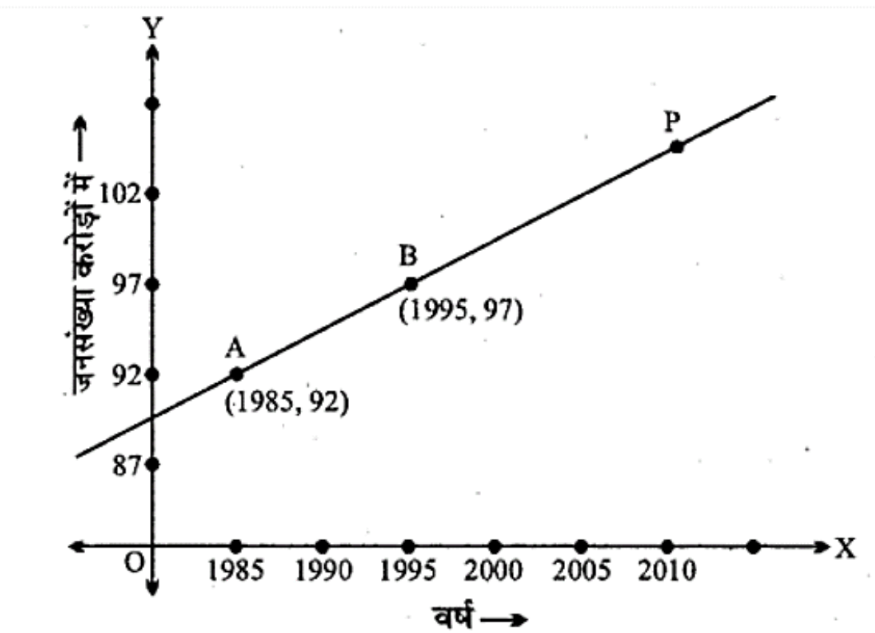
उत्तर: स्पष्टतया A $(1985,92)$ , B $(1995,97)$ और P ${{(2010,y)}}$ संरेखीय है 

AB की ढाल = BP की ढाल 

$\Rightarrow \;\dfrac{{97 - 92}}{{1995 - 1985}}\; = \;\dfrac{{{{y - 97}}}}{{{{2010 - 1995}}}}\; \Rightarrow \;\dfrac{1}{2}\; = \;\dfrac{{{{y - 97}}}}{{{{15}}}}$

$\Rightarrow \;{{2y}} - 194\; = \;15$

$\Rightarrow \;{{y}}\; = \;\dfrac{{209}}{2} = \;\;104.5$ 

2010 मे जनसंख्या = $104.5$

प्रश्नावली 10.2 

1 से 8 तक रेखा का समीकरण ज्ञात कीजिए जो दिए गए प्रतिबंधों को संतुष्ट करता है:

1. ${{x}}$ और ${{y}}$ अक्षों के समीकरण लिखिए। 

उत्तर: ${{x}}$ – अक्ष का समीकरण, ${{y  =  0 }}$

${{y}}$ - अक्ष का समीकरण, ${{x   =  0 }}$

2. ढाल $\dfrac{1}{2}$ और बिन्दु $( - 4,3)$ से जाने वाली। 

उत्तर: यह ढाल ${{m }}$= $\dfrac{1}{2}$ और बिन्दु $( - 4,3)$ है। 

बिन्दु ढाल सूत्र से, ${{(y - 3) = }}\dfrac{{{1}}}{{{2}}}{{(x - ( - 4))}}$

${{2y - 6 = x + 4}}$

अभीष्ट समीकरण,

${{2y - x - 10}}\;{{ = }}\;{{0}}$

${{x - 2y + 10}}\;{{ = }}\;{{0}}$

3. बिन्दु $(0,0)$ से जाने वाली और ढाल ${{m}}$ वाली। 

उत्तर: यह बिन्दु $(0,0)$ और ढाल ${{m}}$ = ${{m}}$ है 

बिन्दु ढाल सूत्र से, ${{(y - 0)}}\;{{ = }}\;{{m(x - 0)}}$

अभीष्ट समीकरण, ${{y}}\;{{ = }}\;{{mx }}$

4. बिन्दु ${{(2,2}}\sqrt 3 )$ से जाने वाली और ${{x}}$ - अक्ष से ${{75}}^\circ$ के कोण पर झुकी हुई। 

उत्तर: बिन्दु ${{(2,2}}\sqrt 3 )$ और रेखा ${{x}}$ - अक्ष से ${{75}}^\circ$ के कोण पर झुकी हुई।

ढाल ${{m}}$ = $\tan {75^\circ }\; = \;\tan (45 + 30)$ = $\dfrac{{\tan 45 + \tan 30}}{{1 - \tan 45.\tan 30}} = \dfrac{{1 + \dfrac{1}{{\sqrt 3 }}}}{{1 - 1 \cdot \dfrac{1}{{\sqrt 3 }}}} = \dfrac{{\sqrt 3  + 1}}{{\sqrt 3  - 1}}$

$\Rightarrow \;{{(y - 2}}\sqrt {{3}} {{)}}\;{{ = }}\;\dfrac{{\sqrt {{3}} {{ + 1}}}}{{\sqrt {{3}} {{ - 1}}}}{{(x - 2)}}$

$\Rightarrow \;{{(}}\sqrt {{3}} {{ - 1)(y - 2}}\sqrt {{3}} {{)}}\;{{ = }}\;{{(}}\sqrt {{3}} {{ + 1)(x - 2)}}$

$\Rightarrow \;{{(}}\sqrt {{3}} {{ - 1)y - (}}\sqrt {{3}} {{ - 1)2}}\sqrt {{3}} \;{{ = }}\;{{(}}\sqrt {{3}} {{ + 1)x - (}}\sqrt {{3}} {{ + 1) \times 2}}$

$\Rightarrow \;{{(}}\sqrt {{3}} {{ - 1)y - (}}\sqrt {{3}} {{ + 1)x}}\;{{ = }}\;{{(}}\sqrt {{3}} {{ - 1)2}}\sqrt {{3}} {{ - (}}\sqrt {{3}} {{ + 1)}}{{.2}}$

$\Rightarrow \;(\sqrt 3  - 1){{y - (}}\sqrt {{3}} {{ + 1)x}}\;{{ = }}\;{{6 - 2}}\sqrt {{3}} {{ - 2}}\sqrt {{3}} {{ - 2}}$

$\Rightarrow \;(\sqrt 3 {{ - 1)y - (}}\sqrt {{3}} {{ + 1)x}}\;{{ = }}\;{{4 - 4}}\sqrt {{3}} $

अशिष्ट समीकरण,  ${{(}}\sqrt {{3}} {{ + 1)x - (}}\sqrt {{3}} {{ - 1)y}}\;{{ = }}\;{{4(}}\sqrt {{3}} {{ - 1)}}$

5. मूल बिन्दु के बाई और ${{x}}$ - अक्ष को $3$ इकाई की दूरी पर प्रतिच्छेद करने तथा ढाल- $2$ वाली। 

उत्तर: गेसा कपो ${{( - 3,0)}}$ से पास कर रहा है। 

ढाल ${{m  =   - 2 }}$ है 

समीकरण के बिन्दु ढाल रूप से हमलोग जानते है कि $\left( {{{y - }}{{{y}}_{{0}}}} \right)\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{0}}}} \right)$

अभीष्ट समीकरण, ${{y + 2x + 6}}\;{{ = }}\;{{0}}$

6. मूल बिन्दु के ऊपर और ${{y}}$ - अक्ष को $2$ इकाई की दूरी पर प्रतिच्छेद करने वाली और ${{x}}$ की धन दिशा के साथ ${{30}}^\circ$ का कोण बनाने वाली 

उत्तर: इसमे रेखा ${{x}}$ - अक्ष के साथ ${{30}}^\circ$ का कोण बना रही है। 

ढाल ${{m}}\; = \;\tan {30^\circ }\; = \;\dfrac{1}{{\sqrt 3 }}$

${{y}}$ - अक्ष को $2$ इकाई की दूरी पर प्रतिच्छेद कर रही है इसलिए ${{c}}\;{{ = }}\;{{2}}$

समीकरण के ढाल अन्तः खंड रूप से जानते है की ${{y }}\;{{ =  mx  + }}\;{{c}}$

इसका समीकरण, ${{y}}\;{{ = }}\;\dfrac{{{1}}}{{\sqrt {{3}} }}{{x + 2}}$ होगा 

अभीष्ट समीकरण, $\sqrt {{3}} {{y - x - 2}}\sqrt {{3}} \;{{ = }}\;{{0}}$

7. बिन्दुओ $( - 1,1)\;,\;(2, - 4)$ से जाते हुए। 

उत्तर: ढाल ${{m}}\;{{ = }}\;\dfrac{{{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}}}{{{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}}}\;{{ = }}\;\dfrac{{{{1 - ( - 4)}}}}{{{{ - 1 - 2}}}}{{ = }}\;\;{{ - }}\dfrac{{{5}}}{{{3}}}$

समीकरण के ढाल बिन्दु रूप से हम जानते है कि 

$\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{1}}}} \right)$

$\Rightarrow \;{{(y - 1)}}\;{{ = }}\;{{ - }}\dfrac{{{5}}}{{{3}}}{{(x - ( - 1))}}$

अभीष्ट समीकरण ${{3y + 5x + 2}}\;{{ = }}\;{{0}}$

8. उस रेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिन्दु से लांबिक दूरी $5$ - इकाई और लंब, धन ${{x}}$ - अक्ष से ${{30}}^\circ$ का कोण बनती है। 

उत्तर: इसमे लम्ब ${{x}}$ - अक्ष के साथ ${{30}}^\circ$ का कोण बना रही है

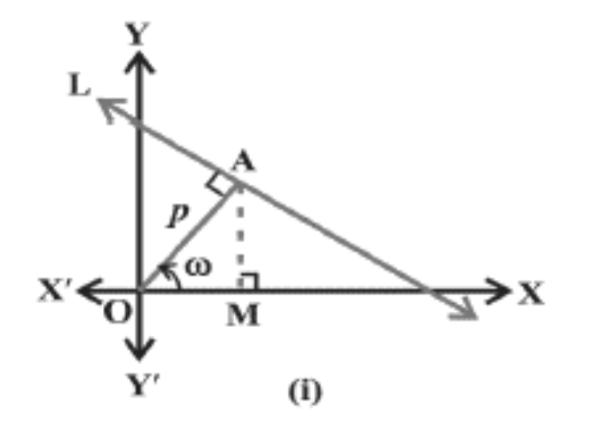
$\sin {30^0}\; = \;\dfrac{1}{2}$

$\cos {30^\circ }\; = \;\dfrac{{\sqrt 3 }}{2}$

लम्बिक दूरी = $5$ - इकाई                                  

हमलोग जानते है कि $\Rightarrow \;{{xcos3}}{{{0}}^{{^\circ }}}{{ + ysin3}}{{{0}}^{{^\circ }}}\; = \;5$         

$\Rightarrow \;\dfrac{{\sqrt {{3}} }}{{{2}}}{{x + }}\dfrac{{{1}}}{{{2}}}{{y - 5}}\; = \;0$

अभीष्ट समीकरण, $\sqrt {{3}} {{x + y - 10}}\;{{ = }}\;{{0}}$

9. PQR के शीर्ष P, Q, R क्रमश $(2,1),( - 2,3),(4,5)$ है। शीर्ष R से जाने वाली मध्यिका का समीकरण ज्ञात कीजिए। 

उत्तर: 

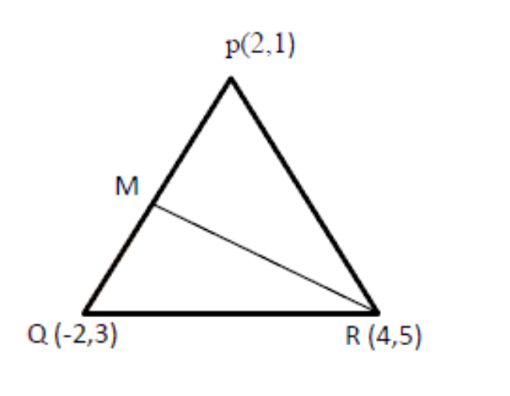
M का ${{x }}$निर्देशांक = $\dfrac{{{{{x}}_{{1}}}{{ + }}{{{x}}_{{2}}}}}{{{2}}}\;{{ = }}\;\dfrac{{{{2 + ( - 2)}}}}{{{2}}}\;{{ = }}\;{{0}}$

M का ${{y }}$ निर्देशांक = $\dfrac{{{{{y}}_{{1}}}{{ + }}{{{y}}_{{2}}}}}{{{2}}}\;{{ = }}\;\dfrac{{{{1 + 3}}}}{{{2}}}\;{{ = }}\;{{2}}$

MR का समीकरण दो बिन्दु रूप से, $\Rightarrow \;{{(y - 2)}}\;{{ = }}\;\left( {\dfrac{{{{5 - 2}}}}{{{{4 - 0}}}}} \right){{(x - 0)}}$

अभीष्ट समीकरण, ${{4y - 3x}}\;{{ = }}\;{{8}}$

10. $( - 3,5)$ से होकर जाने वाली और बिन्दु $(2,5),( - 3,6)$ से जाने वाली रेखा पर लंब रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: माना A, B क्रमश $(2,5),( - 3,6)$ और ढाल ${{m }}$ = $( - 3,5)$ और n, AB के बीच बिन्दु है 

AB का ढाल = ${{m}}\;{{ = }}\;\dfrac{{{{6 - 5}}}}{{{{ - 3 - 2}}}}\;{{ = }}\;\dfrac{{{1}}}{{{{ - 5}}}}$

mn का ढाल = $- \dfrac{1}{{\dfrac{1}{{ - 5}}}}\; = \;5$

mn का समीकरण ढाल बिन्दु रूप से हमलोग जानते है की 

$\left( {{{y - }}{{{y}}_{{0}}}} \right)\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{0}}}} \right)$

 $\Rightarrow \;{{(y - 5)}}\;{{ = }}\;{{5(x - ( - 3))}}$

अभीष्ट समीकरण, ${{y - 5x}}\;{{ = }}\;{{20}}$

11. एक रेखा $(1,0),(2,3)$ बिन्दुओ को मिलाने वाली रेखा खंड पर लंब है तथा उसको $1:{{n}}$ के अनुपाद मे विभाजित करती है। रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: 

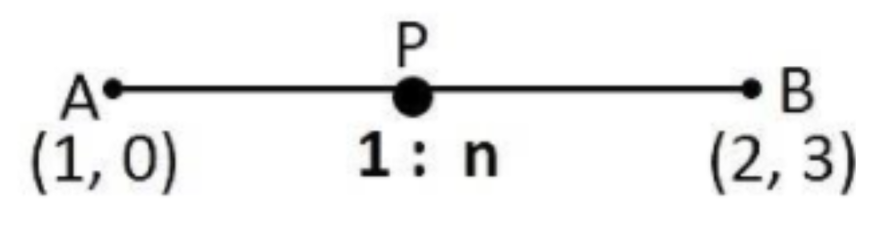
रेखा की ढाल = $\dfrac{{{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}}}{{{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}}}\;{{ = }}\;\dfrac{{{{3 - 0}}}}{{{{2 - 1}}}}\;{{ = }}\;{{3}}$

${{h}}\;{{ = }}\;\dfrac{{{{n \times 1 + 2x1}}}}{{{{n + 1}}}}\;{{ = }}\;\dfrac{{{{n + 2}}}}{{{{n + 1}}}}$

${{k}}\;{{ = }}\;\dfrac{{{{n \times 0 + 3 \times 1}}}}{{{{n + 1}}}}\;{{ = }}\;\dfrac{{{3}}}{{{{n + 1}}}}$

इस रेखा के लम्बवत रेखा की ढाल = ${{ - }}\dfrac{1}{3}$

लम्बवत रेखा का समीकरण जो ${{(h,k)}}$ से पास कर रही है 

ढाल बिन्दु रूप से हमलोग जानते है कि

$\left( {{{y - }}{{{y}}_{{0}}}} \right)\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{0}}}} \right)$

$\Rightarrow \;\left( {{{y - }}\dfrac{{{3}}}{{{{n + 1}}}}} \right)\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{{3}}}\left( {{{x - }}\dfrac{{{{n + 2}}}}{{{{n + 1}}}}} \right)$

 $\Rightarrow \;{{3}}\left( {{{y - }}\dfrac{{{3}}}{{{{n + 1}}}}} \right)\;{{ = }}\;{{ - 1}}\left( {{{x - }}\dfrac{{{{n + 2}}}}{{{{n + 1}}}}} \right)$

अभीष्ट समीकरण, ${{(1 + n)x + 3(1 + n)y}}\;{{ = }}\;{{n + 11}}$

12. एक रेखा का समीकरण ज्ञात कीजिए जो निर्देशांकों से समान अतः खंड काटती है और बिन्दु $(2,3)$ से जाती है। 

उत्तर: 

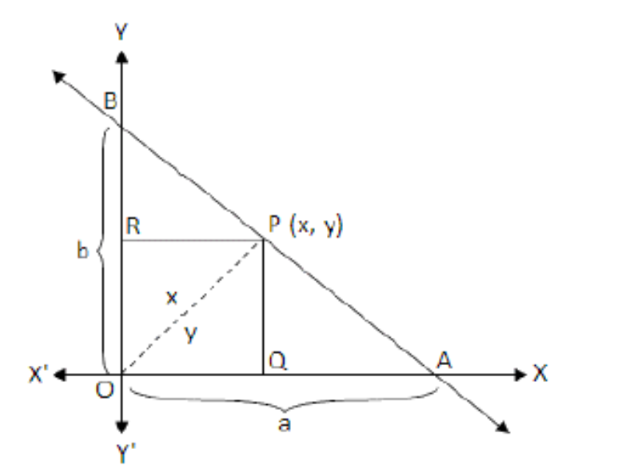
रेखा $(2,3)$  से पास कर रही है और निर्देशांकों से सामान अन्तः खंड काट रही है, हम अन्तः खंड रूप से जानते है कि $\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}\;{{ = }}\;{{1}}$

यह ${{a }}\;{{ = }}\;{{b }}\;{{ = }}\;{{k }}$

$\Rightarrow \;{{x + y}}\;{{ = }}\;{{k }}$

प्रश्न से, $\Rightarrow \;2{{ + 3}}\;{{ = }}\;{{k}}\;{{ = }}\;{{5  }}$

अभीष्ट समीकरण, ${{x + y}}\;{{ = }}\;{{5}}$

13. बिन्दु $(2,2)$ से जाने वाली रेखा का समीकरण ज्ञात कीजिए जिसके द्वारा अक्षों से कटे अतः खंडों का योग $9$ है। 

उत्तर: हमलोग जानते है, अन्तः खंड रूप से प्रश्न से

${{a + b}}\;{{ = }}\;{{9}}$

${{b}}\;{{ = }}\;{{9 - a}}$ 

रेखा $(2,2)$ से पास से पास कर रही है और ${{b}}$ का मान ऊपर के समीकरण मे रखने पर 

$\Rightarrow \;\dfrac{{{2}}}{{{a}}}{{ + }}\dfrac{{{2}}}{{{{9 - a}}}}\;{{ = }}\;{{1}}$

$\Rightarrow \;{{{a}}^{{2}}}{{ - 9a + 18}}\;{{ = }}\;{{0}}$

$\Rightarrow \;({{a - 6)(a - 3)}}\;{{ = }}\;0\;$

${{a = 6, a}}\;{{ = }}\;{{3}}\;$

${{b}}\;{{ = }}\;{{3,}}\;{{b}}\;{{ = }}\;{{6}}$

रेखा का समीकरण $\dfrac{{{x}}}{{{6}}}{{ + }}\dfrac{{{y}}}{{{3}}}\;{{ = }}\;{{1,}}\;\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{6}}}\;{{ = }}\;{{1}}$

अभीष्ट समीकरण ${{x + 2y - 6}}\;{{ = }}\;{{0, 2x + y - 6}}\;{{ = }}\;{{0}}$

14. बिन्दु $(0,2)$ से जाने वाली और धन ${{x}}$ - अक्ष से $\dfrac{{2\pi }}{3}$ के कोण बनाने वाली रेखा का समीकरण ज्ञात कीजिए। इसके समांतर और ${{y}}$ - अक्ष को मूल बिन्दु से ${{2 }}$ इकाई नीचे की दूरी पर प्रतिच्छेद करती हुई रेखा का समीकरण भी ज्ञात कीजिए। 

उत्तर: रेखा $\dfrac{{2\pi }}{3}$ कोण बना रही है 

ढाल = ${{m}}\;{{ = }}\;{{tan}}\left( {\dfrac{{{{2\pi }}}}{{{3}}}} \right)\;{{ = }}\;{{ - }}\sqrt {{3}}$

रेखा $(0,2)$ से पास कर रही है इसलिए ढाल बिन्दु रूप से हमलोग जानते है कि 

$\left( {{{y}} - {{{y}}_0}} \right)\; = \;{{m}}\left( {{{x}} - {{{x}}_0}} \right)$

$\Rightarrow \;{{y}} - 2\; = \; - \sqrt 3 ({{x}} - 0)$

अभीष्ट समीकरण ${{y + }}\sqrt {{3}} {{x - 2}}\;{{ = }}\,{{0}}$

इस रेखा के समांतर वाली रेखा का ढाल = $- \sqrt {{3}}$

वह ${{y}}$ - अक्ष को मूल बिन्दु से ${{2 }}$ इकाई नीचे की दूरी पर प्रतिच्छेद करती है ${{c}}\;{{ = }}\;{{ - 2}}$

समांतर रेखा का समीकरण होगा ${{y}}\;{{ = }}\;{{ - }}\sqrt {{3}} {{x + ( - 2)}}$

अभीष्ट समीकरण ${{y + }}\sqrt {{3}} {{x + 2}}\;{{ = }}\;{{0}}$

15. मूल बिन्दु से किसी रेखा पर डाल गया लंब रेखा से बिन्दु ${{( - 2,9)}}$ पर मिलता है, रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: 

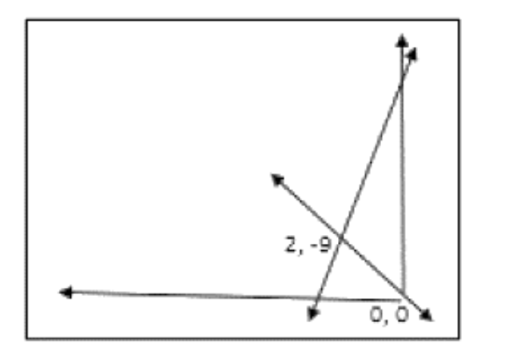
${{(0,0),( - 2,9)}}$ से पास करने वाली रेखा ढाल = ${{m}}\;{{ = }}\;\dfrac{{{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}}}{{{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}}}$ = $\dfrac{{9 - 0}}{{ - 2 - 0}}\; = \; - \dfrac{9}{2}$

लम्ब रेखा का ढाल = $\dfrac{2}{9}$

लम्ब रेखा का समीकरण ढाल बिन्दु रूप से हमलोग जानते है कि $\left( {{{y - }}{{{y}}_{{0}}}} \right)\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{0}}}} \right) \Rightarrow \;{{(y - 9)}}\;{{ = }}\;\dfrac{{{2}}}{{{9}}}{{(x - ( - 2))}}$

अशिष्ट समीकरण $2x - 9y + 85\; = \;0$

16. तांबे की छड़ की लंबाई L (सेमी है) सेलसिउस ताप C का रेखिक फलन है। एक प्रयोग मे यदि L = ${{124}}{{.942 }}$ जन C = ${{20 }}$ और L = ${{125}}{{.134 }}$ जब C = ${{110 }}$हो तो L को C के पदों मे व्यक्त कीजिए। 

उत्तर: प्रश्न से 

जब C = ${{20 }}$ तब L = ${{124}}{{.942 }}$

जब C = ${{110 }}$ तब L = ${{125}}{{.134 }}$

माना कि C, ${{x}}$ - अक्ष पर और L, ${{y }}$ - अक्ष पर है तब ${{ (20, 124}}{{.942), (110, 125}}{{.34) }}$ रेखिक समीकरण को संतुष्ट करेगी, ऊपर के दोनों बिन्दु से पास करती हुई रेखा का समीकरण दो बिन्दु समीकरण रूप से हमलोग जानते है कि 

$\left(y-y_{0}\right)=\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{0}\right)$

$\Rightarrow(y-124.942)=\left(\dfrac{125.34-124.942}{110-20}\right)(x-20)$

$\Rightarrow(y-124.942)=\dfrac{0.192}{90}(x-20)$

अभीष्ट समीकरण L = $\dfrac{{{{0}}{{.192}}}}{{{{90}}}}{{(C - 20) + 124}}{{.942}}$

17. किसी दूध भंडार का स्वामी प्रति सप्ताह ${{980 }}$ लिटर दूध, ${{14 }}$रु प्रति लिटर के भाव से और ${{1220 }}$ लिटर दूध ${{16 }}$ रु प्रति लिटर के भाव से बेच सकता है। विक्रय मूल्य तथा मांग के मध्य के संबंध को रेखिक मानते हुए यह ज्ञात कीजिए कि प्रति सप्ताह वह कितना दूध ${{17 }}$ रु प्रति लिटर के भाव से बेच सकता है? 

उत्तर: प्रश्न से,

स्वामी प्रति सप्ताह दूध बेचता है ${{980 }}$ लिटर दूध, ${{14 }}$रु प्रति लिटर के भाव से और ${{1220 }}$ लिटर दूध ${{16 }}$ रु प्रति लिटर के भाव से 

माना की बेचने की दर ${{x }}$- अक्ष पर तथा टोटल दूध ${{y }}$- अक्ष पर है तब बिन्दु ${{(14,980),(16,1220)}}$ रेखिक समीकरण को संतुष्ट करेंगी ऊपर के दोनों बिन्दु से पास करती हुई रेखा का समीकरण दो बिन्दु समीकरण रूप से हमलोग जानते है कि 

$\left( {{{y - }}{{{y}}_{{0}}}} \right)\;{{ = }}\;\dfrac{{{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}}}{{{{{x}}_{{{2 - }}{{{x}}_{{1}}}}}}}\left( {{{x - }}{{{x}}_{{0}}}} \right)$

$\Rightarrow \;{{(y - 980)}}\;{{ = }}\;\left( {\dfrac{{{{1220 - 980}}}}{{{{16 - 14}}}}} \right){{(x - 14)}}$

$\Rightarrow \;{{(y - 980)}}\;{{ = }}\;\left( {\dfrac{{{{240}}}}{{{2}}}} \right){{(x - 14)}}$

अशिष्ट समीकरण ${{y}}\;{{ = }}\;{{120(x - 14) + 980}}$

प्रश्न से जब ${{x}}\;{{ = }}\;{{17}}$ रु प्रति लीटर, $y\; = \;120(17 - 14) + 980\; \Rightarrow \;{{y}}\;{{ = }}\;1340$

वह $1340$ लिटर दूध बेच सकता है।

18. अक्षों के बीच रेखाखण्ड को मध्य बिन्दु P ${{(a,b)}}$ है। दिखाइए कि रेखा का समीकरण $\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}{{ = 2}}$ है 

उत्तर: 

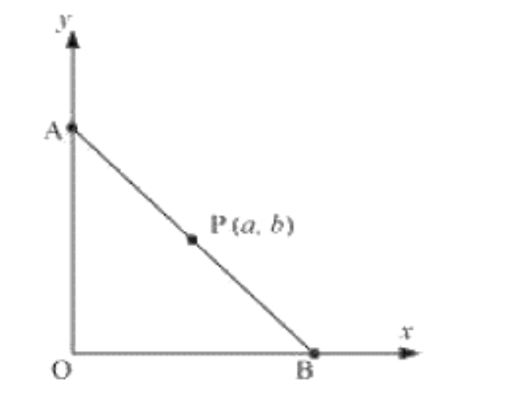
माना AB वह रेखाखण्ड है P ${{(a,b)}}$ मध्य बिन्दु है 

OA = ${{y}}$ तथा OB = ${{x }}$ माना

${{a}}\;{{ = }}\;{{x/2,}}\;{{b}}\;{{ = }}\;{{y/2}}\;$

$\Rightarrow \;{{x = 2a,}}\;{{y}}\;{{ = }}\;{{2b}}$ 

अन्तः खंड रूप से 

$\dfrac{{{x}}}{{{{2a}}}}{{ + }}\dfrac{{{y}}}{{{{2b}}}}\;{{ = }}\;{{1}}$

$\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}\;{{ = }}\;{{2}}$

19. अक्षों के बीच रेखाखण्ड को बिन्दु R ${{(h,k)}}$ , ${{1:2 }}$ के अनुपाद मे विभक्त करता है। रेखा कासमीकरण ज्ञात कीजिए। 

उत्तर:

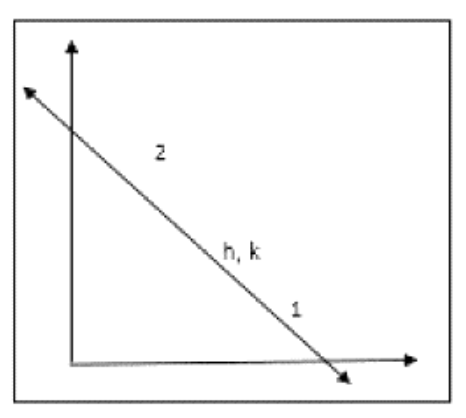
माना की AB वह रेकजाखण्ड है R ${{(h,k)}}$ वह बिन्दु है जो रेखा को ${{2:1 }}$ मे बाटता है 

OA = ${{y }}$ तथा OB = ${{x }}$ माना 

${{h  =  }}\dfrac{{{{1x0 + 2xx}}}}{{{{1 + 2}}}}\;{{ = }}\;\dfrac{{{{2x}}}}{{{3}}}\;{{,}}\;{{k}}\;{{ = }}\;\dfrac{{{{1xy + 2x0}}}}{{{{1 + 2}}}}\;{{ = }}\;\dfrac{{{y}}}{{{3}}}$ 

${{x  =  }}\dfrac{{{{3h}}}}{{{2}}}\;{{,}}\;{{y = }}\;{{3k}}$

अन्तः खंड रूप से 

$\dfrac{{{{2x}}}}{{{{3h}}}}{{ + }}\dfrac{{{y}}}{{{{3k}}}}\;{{ = }}\;{{1}}$

$\dfrac{{{{2x}}}}{{{h}}}{{ + }}\dfrac{{{y}}}{{{k}}}\;{{ = }}\;3$

अशिष्ट समीकरण ${{2xk + hy}}\;{{ = }}\;{{3hk}}$

20. रेखा के समीकरण की संकल्पना का प्रयोग करते हुए सिद्ध कीजिए कि तीन बिन्दु ${{(3,0),( - 2, - 2),(8,2)}}$ संरेख है। 

उत्तर: प्रश्न मे दिया हुआ बिन्दु A, B, C क्रमश ${{(3,0),( - 2, - 2),(8,2)}}$ है 

AB का समीकरण,

$\Rightarrow \;{{(y - 0)}}\;{{ = }}\;\dfrac{{{{ - 2 - 0}}}}{{{{ - 2 - 3}}}}{{(x - 3)}}$

$\Rightarrow \;{{y}}\;{{ = }}\;{{ - 2/ - 5(x - 3)}}$ 

$\Rightarrow \;{{2x - 5y}}\;{{ = }}\;{{6}}$  ………………………..(i)

अब C बिन्दु को इस समीकरण मे रखते है 

$2 \times 8 - 5 \times 2\; = \;6$

बिन्दु C भी (i) को संतुष्ट करती है 

इस तरह हम कह सकते है की तीनों बिन्दु संरेख है।

प्रश्नावली 10.3 

1. निमनलिखित समीकरणों को ढाल अतः खंड रूप मे रूपांतरित कीजिए और उनका ${{y}}$ - अतः खंड ज्ञात कीजिए। 

(i) ${{x + 7y}}\;{{ = }}\;{{0 }}$

उत्तर: दिया गया समीकरण है ${{x + 7y}}\;{{ = }}\;{{0 }}$

इसे इस प्रकार लिखा जा सकता है ${{y}}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{{7}}}{{x + 0}}$ ........ (1)

यह समीकरण ${{y}}\;{{ = }}\;{{mx + c}}$ रूप का है और जहा ${{m}}\;{{ = }}\;\dfrac{{ - 1}}{7}{{, c}}\;{{ = }}\;{{0}}$

इसलिए, समीकरण (1) ढलान खंड रूप है, जहा ढलान और ${{y}}$ - खंड क्रमश: $\;\dfrac{{ - 1}}{7}{{, 0}}$ है।

(ii) ${{6x + 3y - 5}}\;{{ = }}\;{{0 }}$

उत्तर: दिया गया समीकरण ${{6x + 3y - 5}}\;{{ = }}\;{{0 }}$ है

इसे इस प्रकार लिखा जा सकता है ${{y}}\;{{ = }}\;\dfrac{{{1}}}{{{3}}}{{( - 6x + 5)}}$

${{y}}\;{{ = }}\;{{ - 2x + }}\dfrac{{{5}}}{{{3}}}$ ..........(2)

यह समीकरण ${{y}}\;{{ = }}\;{{mx + c}}$ रूप का है और जहा ${{m}}\;{{ = }}\; - 2{{, c}}\;{{ = }}\;\dfrac{5}{3}$

इसलिए, समीकरण (2) ढलान खंड रूप है, जहा ढलान और ${{y}}$ - खंड क्रमश: $\; - 2,\;\dfrac{5}{3}$ है।

(iii) ${{y}}\;{{ = }}\;{{0 }}$

उत्तर: दिया गया समीकरण ${{y}}\;{{ = }}\;{{0 }}$है

इसे इस प्रकार लिखा जा सकता है ${{y - 0}}{{.x}}\;{{ = }}\;{{0}}$ ........(3)

यह समीकरण ${{y}}\;{{ = }}\;{{mx + c}}$ रूप का है और जहा ${{m}}\;{{ = }}\;0{{, c}}\;{{ = }}\;0$

इसलिए, समीकरण (2) ढलान खंड रूप है, जहा ढलान और ${{y}}$ - खंड क्रमश: $0,\;0$ है।

2. निमनलिखित समीकरणों को अतः खंड रूप मे रूपांतरित कीजिए और अक्षों पर इनके द्वारा काटे गए अतः खंड ज्ञात कीजिए: 

(i) ${{3x + 2y - 12}}\;{{ = }}\;{{0 }}\;{{ }}$

उत्तर: दिया गया समीकरण है ${{3x + 2y - 12}}\;{{ = }}\;{{0 }}\;{{ }}$

इसे इस प्रकार लिखा जा सकता है

${{3x + 2y}}\;{{ = }}\;{{12}}$

$\dfrac{{{{3x}}}}{{{{12}}}}{{ + }}\dfrac{{{{2y}}}}{{{{12}}}}\;{{ = }}\;{{1}}$ 

$\dfrac{x}{4} + \dfrac{y}{6}\; = \;1$ ..............(1)

यह समीकरण $\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}\;{{ = }}\;{{1}}$ फार्म का है, जहा ${{a}}\;{{ = }}\;{{4,}}\;{{b}}\;{{ = }}\;{{6}}$ है 

इसलिए समीकरण (1) खंड रूप मे है जहा ${{x, y}}$ अक्ष पर खंड क्रमश: ${{4,}}\;{{6 }}$ है

(ii) ${{4x - 3y}}\;{{ = }}\;6{{ }}\;{{ }}$

उत्तर: दिया गया समीकरण है ${{4x - 3y}}\;{{ = }}\;6{{ }}\;{{ }}$

इसे इस प्रकार लिखा जा सकता है

$\dfrac{{{{4x}}}}{{{6}}}{{ + }}\dfrac{{{{3y}}}}{{{6}}}\;{{ = }}\;{{1}}$

$\dfrac{{{{2x}}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{2}}}\;{{ = }}\;{{1}}$ 

$\dfrac{{{x}}}{{\dfrac{{{3}}}{{{2}}}}}{{ + }}\dfrac{{{y}}}{{{{ - 2}}}}\;{{ = }}\;{{1}}$ ..........(2)

इसलिए समीकरण (2) खंड रूप मे है जहा ${{x, y}}$ अक्ष पर खंड क्रमश: $\dfrac{3}{2}{{,}}\; - 2$ है

(iii) ${{3y + 2}}\;{{ = }}\;0{{ }}\;{{ }}$ 

उत्तर: दिया गया समीकरण है ${{3y + 2}}\;{{ = }}\;0{{ }}\;{{ }}$

इसे इस प्रकार लिखा जा सकता है ${{3y}}\;{{ = }}\;{{ - 2 }}$

$\dfrac{y}{{ - \dfrac{2}{3}}}\; = \;1$ ............(3) 

इसलिए समीकरण (3) खंड रूप मे है जहा ${{y}}$ - अक्ष पर खंड क्रमश: $\dfrac{{ - 2}}{3}$ है और ${{x}}$ - अक्ष पर कोई खंड नही है। 

3. निमनलिखित समीकरणों को लम्ब रूप मे रूपांतरित इजीए। उनकी मूल बिन्दु से लंबहिक दूरिया और लम्ब तथा धन ${{x}}$ - अक्ष के बीच का कोण ज्ञात कीजिए:

(i) ${{x - }}\sqrt {{3}} {{y + 8}}\;{{ = }}\;{{0}}$

उत्तर: दिया गया समीकरण है ${{x - }}\sqrt {{3}} {{y + 8}}\;{{ = }}\;{{0}}$

इसे इस प्रकार लिखा जा सकता है 

${{x - }}\sqrt {{3}} {{y}}\;{{ = }}\;{{ - 8}}$

${{ - x + }}\sqrt {{3}} {{y}}\;{{ = }}\;{{8}}$ 

दोनों पक्षों $\sqrt {{{( - 1)}^2} + {{(\sqrt 3 )}^2}} \; = \;\sqrt 4 \; = \;2$ द्वारा विभाजित करने पर

${{ - }}\dfrac{{{x}}}{{{2}}}{{ + }}\dfrac{{\sqrt {{3}} }}{{{2}}}{{y}}\;{{ = }}\;\dfrac{{{8}}}{{{2}}}$

$\left( {{{ - }}\dfrac{{{1}}}{{{2}}}} \right){{x + }}\left( {\dfrac{{\sqrt {{3}} }}{{{2}}}} \right){{y}}\;{{ = }}\;{{4}}$

${{xcos12}}{{{0}}^{{^\circ }}}{{ + ysin12}}{{{0}}^{{^\circ }}}\;{{ = }}\;{{4}}$ ..........(1) 

समीकरण (1) समान्य रूप मे है, रेखा के समीकरण के समान्य रूप ${{xcos\omega  + ysin\omega }}\;{{ = }}\;{{p}}$ के साथ समीकरण (1) की तुलना करने पर हम ${{\omega }}\;{{ = }}\;{{12}}{{{0}}^{{^\circ }}}{{,}}\;{{p}}\;{{ = }}\;{{4}}$ प्राप्त करते है। 

इस प्रकार मूल से रेखा की लम्बवत दूरी ${{4}}$ है जबकि लम्बवत और धनात्मक ${{x}}$ - अक्ष के बीच का कोण ${{120}}^\circ$ है।

(ii) ${{y - 2}}\;{{ = }}\;{{0}}$

उत्तर: दिया गया समीकरण ${{y - 2}}\;{{ = }}\;{{0}}$ है 

इसे ${{0}}{{.x + 1}}{{.y}}\;{{ = }}\;{{2}}$ के रूप मे कम किया जा सकता है, $\sqrt {{0^2} + {1^2}} \; = \;1$ से दोनों पक्षों को विभाजित करने पर हमने प्राप्त किया ${{0}}{{.x + 1}}{{.y}}\;{{ = }}\;{{2}}$ 

${{xcos9}}{{{0}}^{{^\circ }}}{{ + ysin9}}{{{0}}^{{^\circ }}}\;{{ = }}\;{{2}}$ ............(2)

समीकरण (2) समान्य रूप मे है, समीकरण के समान्य रूप ${{xcos\omega  + ysin\omega }}\;{{ = }}\;{{p}}$ के साथ समीकरण (2) की तुलना करने पर हम ${{\omega }}\;{{ = }}\;9{{{0}}^{{^\circ }}}{{,}}\;{{p}}\;{{ = }}\;2$ प्राप्त करते है। 

इस प्रकार मूल से रेखा की लम्बवत दूरी $2$ है जबकि लम्बवत और धनात्मक ${{x}}$ - अक्ष के बीच का कोण ${{90}}^\circ$ है।

(iii) ${{x - y}}\;{{ = }}\;4$

उत्तर: दिया गया समीकरण ${{x - y}}\;{{ = }}\;4$ है

इसे कम किया जा सकता है ${{ 1}}{{.x  + ( - 1)y}}\;{{ = }}\;{{4}}$

$\sqrt {{1^2} + {1^2}} \; = \;\sqrt 2$ द्वारा दोनों पक्षों को विभाजित करने पर हमने प्राप्त किया 

$\dfrac{{{1}}}{{\sqrt {{2}} }}{{x + }}\left( {{{ - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right){{y}}\;{{ = }}\;\dfrac{{{4}}}{{\sqrt {{2}} }}$

${{xcos}}\left( {{{2\pi  - }}\dfrac{{{\pi }}}{{{4}}}} \right){{ + ysin}}\left( {{{2\pi  - }}\dfrac{{{\pi }}}{{{4}}}} \right)\;{{ = }}\;{{2}}\sqrt {{2}}$

${{xcos31}}{{{5}}^{{^\circ }}}{{ + ysin31}}{{{5}}^{{^\circ }}}\;{{ = }}\;{{2}}\sqrt {{2}}$ ..............(3) 

समीकरण (3) समान्य रूप मे है, समीकरण के समान्य रूप ${{xcos\omega  + ysin\omega }}\;{{ = }}\;{{p}}$ के साथ समीकरण (3) की तुलना करने पर हम ${{\omega }}\;{{ = }}\;{315^{{^\circ }}}{{,}}\;{{p}}\;{{ = }}\;2\sqrt 2$ प्राप्त करते है। 

इस प्रकार मूल से रेखा की लम्बवत दूरी $2\sqrt 2$ है जबकि लम्बवत और धनात्मक ${{x}}$ - अक्ष के बीच का कोण $315^\circ$ है।

4. बिन्दु $( - 1,1)$ की रेखा ${{12(x + 6)}}\;{{ = }}\;{{5(y - 2)}}$ से दूरी ज्ञात कीजिए। 

उत्तर: रेखा का दिया गया समीकरण है ${{12(x + 6)}}\;{{ = }}\;{{5(y - 2)}}$ 

${{12x + 72}}\;{{ = }}\;{{5y - 10}}$

${{12x - 5y + 82}}\;{{ = }}\;{{0}}$ ..............(1)

रेखा के समान्य समीकरण ${{Ax + By + C}}\;{{ = }}\;{{0}}$ के साथ समीकरण (1) की तुलना करने पर, हम प्राप्त करते है ${{A = }}\;{{12,}}\;{{B}}\;{{ = }}\;{{ - 5,}}\;{{C}}\;{{ = }}\;{{ - 82}}$

यह ज्ञात है कि एक बिन्दु ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ से एक रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ की लम्बवत दूरी ${{d}}\;{{ = }}\;\dfrac{{\left| {{{A}}{{{x}}_{{1}}}{{ + B}}{{{y}}_{{1}}}{{ + C}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$ द्वारा दिया गया है 

दी गई बिन्दु है ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ = ${{( - 1,1)}}$

इसलिए दी गई दूरी से बिन्दु ${{( - 1,1)}}$ की दूरी 

${{d}}\;{{ = }}\;\dfrac{{{{|12( - 1) + ( - 5)(1) + 82|}}}}{{\sqrt {{{{{(12)}}}^{{2}}}{{ + ( - 5}}{{{)}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{| - 12 - 5 + 82|}}}}{{\sqrt {{{169}}} }}\;{{ = }}\;\dfrac{{{{|65|}}}}{{{{13}}}}$ = ${{5}}$ इकाई

5. ${{x }}$ - अक्ष पर बिन्दु को ज्ञात कीजिए जिनकी रेखा $\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{4}}}\;{{ = }}\;{{1}}$ से दूरिया ${{4}}$ इकाई है। 

उत्तर: रेखा का दिया गया समीकरण है $\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{4}}}\;{{ = }}\;{{1}}$ या ${{4x + 3y - 12}}\;{{ = }}\;{{0}}$ ............(1)

रेखा के समान्य ${{Ax + By + C}}\;{{ = }}\;{{0}}$ के साथ समीकरण (1) की तुलना मे हम प्राप्त करते है ${{A = }}\;4{{,}}\;{{B}}\;{{ = }}\;3{{,}}\;{{C}}\;{{ = }}\;{{ - 12 }}$

आज्ञा देना ${{(a,0)}}$ ${{x}}$ - अक्ष पर बिन्दु है जिसकी दी गई लाइन से दूरी ${{4 }}$ इकाइया है। 

यह ज्ञात है कि एक बिन्दु ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ से एक रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ की लम्बवत दूरी ${{d}}\;{{ = }}\;\dfrac{{\left| {{{A}}{{{x}}_{{1}}}{{ + B}}{{{y}}_{{1}}}{{ + C}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$ द्वारा दिया गया है इसलिए 

${{4}}\;{{ = }}\;\dfrac{{{{|4a + 3X0 - 12|}}}}{{\sqrt {{{{4}}^{{2}}}{{ + }}{{{3}}^{{2}}}} }}$

$=> \;{{4}}\;{{ = }}\;\dfrac{{{{|4a - 12|}}}}{{{5}}}$

$=> \;{{|4a - 12|}}\;{{ = }}\;{{20}}$

$=> \;{{ \pm (4a - 12)}}\;{{ = }}\;{{20}}$

$=> \;{{(4a - 12)}}\;{{ = }}\;{{20,}}\;{{ - (4a - 12)}}\;{{ = }}\;{{20}}$

$=> \;{{4a}}\;{{ = }}\;{{20 + 124,}}\;{{a}}\;{{ = }}\;{{ - 20 + 12}}$ 

$=> \;{{a}}\;{{ = }}\;{{8,}}\;{{ - 2}}$

इस प्रकार ${{x}}$ - अक्ष पर आवश्यक बिन्दु है ${{( - 2,0),}}\;{{(8,0)}}$

6. समांतर रेखाओ के बीच की दूरी ज्ञात कीजिए: 

(i) ${{15x + 8y - 34}}\;{{ = }}\;{{0, 15x + 8y + 31}}\;{{ = }}\;{{0}}$ 

उत्तर: यह ज्ञात है कि समांतर रेखाओ ${{Ax + By + }}{{{C}}_1}\;{{ = }}\;{{0}}$ और ${{Ax + By + }}{{{C}}_2}\;{{ = }}\;{{0}}$ के बीच की दूरी ${{d}}\;{{ = }}\;\dfrac{{\left| {{{{C}}_{{1}}}{{ - }}{{{C}}_{{2}}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$ द्वारा दिया गया है  

दी गई समांतर रेखाए है ${{15x + 8y - 34}}\;{{ = }}\;{{0, 15x + 8y + 31}}\;{{ = }}\;{{0}}$ 

यहा ${{A}}\;{{ = }}\;{{15,}}\;{{B}}\;{{ = }}\;{{8,}}\;{{{C}}_{{1}}}\;{{ = }}\;{{ - 34,}}\;{{{C}}_{{2}}}\;{{ = }}\;{{31}}$

इसलिए समांतर रेखाओ के बीच की दूरी है 

${{d}}\;{{ = }}\;\dfrac{{\left| {{{{C}}_{{1}}}{{ - }}{{{C}}_{{2}}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{| - 34 - 31|}}}}{{\sqrt {{{{{(15)}}}^{{2}}}{{ + (8}}{{{)}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{| - 65|}}}}{{\sqrt {{{289}}} }}\;{{ = }}\;\dfrac{{{{65}}}}{{{{17}}}}$ इकाइया

(ii) ${{l(x + y) + p}}\;{{ = }}\;{{0, l(x + y) - r}}\;{{ = }}\;{{0}}$

उत्तर: दी गई समानांतर रेखे है ${{l(x + y) + p}}\;{{ = }}\;{{0, l(x + y) - r}}\;{{ = }}\;{{0}}$

${{l(x + y) + p = 0,}}\;{{l(x + y) - r = 0}}$

यहा ${{A}}\;{{ = }}\;{{l,}}\;{{B}}\;{{ = }}\;{{l,}}\;{{{C}}_{{1}}}\;{{ = }}\;{{p,}}\;{{{C}}_{{2}}}\;{{ = }}\;{{ - r}}$

इसलिए समांतर रेखाओ के बीच की दूरी है 

${{d}}\;{{ = }}\;\dfrac{{\left| {{{{C}}_{{1}}}{{ - }}{{{C}}_{{2}}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{|p + r|}}}}{{\sqrt {{{{{(l)}}}^{{2}}}{{ + (l}}{{{)}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{|p + r|}}}}{{\sqrt {{{2}}{{{l}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{1}}}{{\sqrt {{2}} }}\dfrac{{{{|p + r|}}}}{{{l}}}$ इकाई

7. रेखा ${{3x - 4y + 2}}\;{{ = }}\;{{0}}$ के समांतर और बिन्दु ${{( - 2,3)}}$ से जाने वाली रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: दी गई रेखा का समीकरण है ${{3x - 4y + 2}}\;{{ = }}\;{{0}}$

${{y}}\;{{ = }}\;\dfrac{{{{3x}}}}{{{4}}}{{ + }}\dfrac{{{2}}}{{{4}}}$

${{y}}\;{{ = }}\;\dfrac{{{3}}}{{{4}}}{{x + }}\dfrac{{{1}}}{{{2}}}$

जो ${{y}}\;{{ = }}\;{{mx + c}}$ रूप की है 

दी गई रेखा का ढलान = $\dfrac{3}{4}$

यह ज्ञात है कि समानांतर रेखाओ मे समान ढलान होती है 

दूसरी पंक्ति का ढलान ${{m}}\;{{ = }}\;\dfrac{{{3}}}{{{4}}}$

अब उस रेखा का समीकरण जिसमे ढलान है और अंक $( - 2,3)$ से होकर गुजरता है

${{(y - 3)}}\;{{ = }}\;\dfrac{{{3}}}{{{4}}}{{\{ x - ( - 2)\} }}$

$\Rightarrow \;{{4y - 12}}\;{{ = }}\;{{3x + 6}}$

$\Rightarrow \;{{3x - 4y + 18}}\;{{ = }}\;{{0}}$

8. रेखा ${{x - 7y + 5  = }}\;{{0  }}$ पर लम्ब और ${{x}}$ - अंत खंड ${{3 }}$ वाली रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: रेखा का दिया गया समीकरण है ${{x - 7y + 5  = }}\;{{0  }}$

${{y}}\;{{ = }}\;\dfrac{{{1}}}{{{7}}}{{x + }}\dfrac{{{5}}}{{{7}}}$ जो ${{y}}\;{{ = }}\;{{mx + c}}$ रूप की है 

दी गई रेखा का ढलान 

रेखा की ढलान, लम्बवत रेखा की ढलान के लिए $\dfrac{{{1}}}{{{7}}}$ है 

ढलान ${{m}}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{\dfrac{{{1}}}{{{7}}}}}\;{{ = }}\;{{ - 7}}$ और 

${{x}}$ - अंत खंड ${{3 }}$ वाली रेखा का समीकरण

${{y = }}\;{{m(x - d)}}$

$\Rightarrow \;{{y}}\;{{ = }}\;{{ - 7(x - 3)}}$

$\Rightarrow \;{{y}}\;{{ = }}\;{{ - 7x + 21}}$

$\Rightarrow \;{{7x + y}}\;{{ = }}\;{{21}}$ 

द्वारा दिया गया है

9. रेखाओ $\sqrt {{3}} {{x + y}}\;{{ = }}\;{{1,}}\;{{x + }}\sqrt {{3}} {{y}}\;{{ = }}\;{{1}}$ के बीच का कोण ज्ञात कीजिए। 

उत्तर: दी गई रेखाए है $\sqrt {{3}} {{x + y}}\;{{ = }}\;{{1,}}\;{{x + }}\sqrt {{3}} {{y}}\;{{ = }}\;{{1}}$ 

${{ - }}\sqrt {{3}} {{x + 1}}\;{{ = }}\;{{y,}}\;\dfrac{{{1}}}{{\sqrt {{3}} }}{{x + }}\dfrac{{{1}}}{{\sqrt {{3}} }}\;{{ = }}\;{{y}}$

जबकि रेखा की ढलान क्रमश: ${{{m}}_{{1}}}\;{{ = }}\;{{ - }}\sqrt {{3}} {{x,}}\;{{{m}}_{{2}}}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{\sqrt {{3}} }}$ है 

तीव्र कोण अर्थात ${{\theta }}$ दोनों रेखाओ के बीच मे

${{tan\theta }}\;{{ = }}\;\left| {\dfrac{{{{{m}}_{{{1 - }}}}{{{m}}_{{2}}}}}{{{{1 + }}{{{m}}_{{1}}}{{{m}}_{{2}}}}}} \right|$

$\Rightarrow \;{{tan\theta }}\;{{ = }}\;\left| {\dfrac{{{{ - }}\sqrt {{3}} {{ + }}\dfrac{{{1}}}{{\sqrt {{3}} }}}}{{{{1 + ( - }}\sqrt {{3}} {{)}}\left( {{{ - }}\dfrac{{{1}}}{{\sqrt {{3}} }}} \right)}}} \right|$

$\Rightarrow \;{{tan\theta }}\;{{ = }}\;\left| {\dfrac{{\dfrac{{{{ - 3 + 1}}}}{{\sqrt {{3}} }}}}{{{{1 + 1}}}}} \right|\;{{ = }}\;\left| {\dfrac{{{{ - 2}}}}{{{{2x}}\sqrt {{3}} }}} \right|$

$\Rightarrow \;{{tan\theta }}\;{{ = }}\;\dfrac{{{1}}}{{\sqrt {{3}} }}$ 

द्वारा दिया गया है, इस प्रकार दी गई रेखाओ के बीच का कोण या तो $30^\circ \;$ या $180^\circ \; - \;30^\circ \; = \;150^\circ$ है।

10. बिन्दुओ ${{(h,3)}}$ और ${{(4,1)}}$ से जाने वाली रेखा, रेखा ${{7x  - 9y - 19 }}\;{{ = }}\;{{0 }}$ को समकोण पर प्रतिच्छेद करती है तो ${{h}}$ का मान ज्ञात कीजिए। 

उत्तर: बिन्दुओ ${{(h,3)}}$ और ${{(4,1)}}$ से गुजरने वली रेखा की ढलान ${{{m}}_{{1}}}\;{{ = }}\;\dfrac{{{{1 - 3}}}}{{{{4 - h}}}}\;{{ = }}\;{{ - }}\dfrac{{{2}}}{{{{4 - h}}}}$ है 

रेखा ${{7x  - 9y - 19 }}\;{{ = }}\;{{0 }}$ या ${{y}}\;{{ = }}\;\dfrac{{{7}}}{{{9}}}{{x - }}\dfrac{{{{19}}}}{{{9}}}$ की ढलान ${{{m}}_2}\; = \;\dfrac{7}{9}$

यह दिया जाता है कि दो रेखाओ लम्बवत होती है

$\therefore {{{m}}_{{1}}}{{ \times }}{{{m}}_{{2}}}\;{{ = }}\;{{ - 1}}$

$\Rightarrow \;\dfrac{{{{ - 14}}}}{{{{36 - 9h}}}}{{ =  - 1}}$

$\Rightarrow \;{{14}}\;{{ = }}\;{{36 - 9h}}$

$\Rightarrow \;{{9h}}\;{{ = }}\;{{36 - 14}}$

$\Rightarrow \;{{h}}\;{{ = }}\;\dfrac{{{{22}}}}{{{9}}}$

11. सिद्ध कीजिए कि बिन्दु ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ से जाने वाली और रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ के समांतर रेखा कासमिकर्ण ${{A}}\left( {{{x - }}{{{x}}_{{1}}}} \right){{ + B}}\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;{{0}}$ है। 

उत्तर: रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ या ${{y}}\;{{ = }}\;\left( {\dfrac{{{{ - A}}}}{{{B}}}} \right){{x + }}\left( {\dfrac{{{{ - C}}}}{{{B}}}} \right)$ की ढलान ${{m}}\;{{ = }}\;\left( {\dfrac{{{{ - A}}}}{{{B}}}} \right)$

यह ज्ञात है कि समानांतर रेखाओ मे समान ढलान है 

दूसरी पंक्ति की ढलान ${{m}}\;{{ = }}\;\left( {\dfrac{{{{ - A}}}}{{{B}}}} \right)$

बिन्दु ${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$ से गुजरने वाली रेखा का समीकरण और ढलान ${{m}}\;{{ = }}\;\left( {\dfrac{{{{ - A}}}}{{{B}}}} \right)$ है

${{y - }}{{{y}}_{{1}}}\;{{ = }}\;{{m}}\left( {{{x - }}{{{x}}_{{1}}}} \right)$

$\Rightarrow \;{{y - }}{{{y}}_{{1}}}\;{{ = }}\;{{ - }}\dfrac{{{A}}}{{{B}}}\left( {{{x - }}{{{x}}_{{1}}}} \right)$

$\Rightarrow \;{{B}}\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;{{ - A}}\left( {{{x - }}{{{x}}_{{1}}}} \right)$

$\Rightarrow \;{{A}}\left( {{{x - }}{{{x}}_{{1}}}} \right){{ + B}}\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;{{0}}$

इसलिए बिन्दु ${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$ के माध्यम से रेखा और रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ के समानांतर ${{A}}\left( {{{x - }}{{{x}}_{{1}}}} \right){{ + B}}\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;{{0}}$

12. बिन्दु ${{(2,3)}}$ से जाने वाली दो रेखाए परस्पर ${{60}}^\circ$ के कोण पर प्रतिच्छेद करती है। यदि एक रेखा की ढाल $2$ है तो दूसरी रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: यह दिया जाता है कि पहले रेखा की ढलान ${{{m}}_{{1}}}\;{{ = }}\;{{2}}$

दूसरी रेखा की ढलान ${{{m}}_2}$ होने दे 

$\therefore \;{{tan6}}{{{0}}^{{^\circ }}}\;{{ = }}\;\left| {\dfrac{{{{{m}}_{{{1 - }}}}{{{m}}_{{2}}}}}{{{{1 + }}{{{m}}_{{1}}}{{{m}}_{{2}}}}}} \right|$

 $\Rightarrow \;\sqrt {{3}} \;{{ = }}\;\left| {\dfrac{{{{2 - }}{{{m}}_{{2}}}}}{{{{1 + 2}}{{{m}}_{{2}}}}}} \right|$

 $\Rightarrow \;\sqrt {{3}} \;{{ = }}\;{{ \pm }}\left( {\dfrac{{{{2 - }}{{{m}}_{{2}}}}}{{{{1 + 2}}{{{m}}_{{2}}}}}} \right)$

 $\Rightarrow \;\sqrt {{3}} \;{{ = }}\;\left( {\dfrac{{{{2 - }}{{{m}}_{{2}}}}}{{{{1 + 2}}{{{m}}_{{2}}}}}} \right){{,}}\;\sqrt {{3}} \;{{ = }}\;{{ - }}\left( {\dfrac{{{{2 - }}{{{m}}_{{2}}}}}{{{{1 + 2}}{{{m}}_{{2}}}}}} \right)$

 $\Rightarrow \;\sqrt {{3}} \left( {{{1 + 2}}{{{m}}_{{2}}}} \right)\;{{ = }}\;{{2 - }}{{{m}}_{{2}}}{{,}}\;\sqrt {{3}} \left( {{{1 + 2}}{{{m}}_{{2}}}} \right)\;{{ = }}\;\;{{ - }}\left( {{{2 - }}{{{m}}_{{2}}}} \right)$

 $\Rightarrow \sqrt {{3}} {{ + 2}}\sqrt {{3}} {{{m}}_{{2}}}{{ + }}{{{m}}_{{2}}}{{ = 2,}}\;\sqrt {{3}} {{ + 2}}\sqrt {{3}} {{{m}}_{{2}}}{{ - }}{{{m}}_{{2}}}\;{{ = }}\;{{ - 2}}$

 $\Rightarrow \;\sqrt {{3}} {{ + (2}}\sqrt {{3}} {{ + 1)}}{{{m}}_{{2}}}\;{{ = }}\;{{2,}}\;\sqrt {{3}} {{ + (2}}\sqrt {{3}} {{ - 1)}}{{{m}}_{{2}}}\;{{ = }}\;{{ - 2}}$

 $\Rightarrow \;{{{m}}_{{2}}}\;{{ = }}\;\dfrac{{{{2 - }}\sqrt {{3}} }}{{{{2}}\sqrt {{3}} {{ + 1}}}}{{,}}\;{{{m}}_{{2}}}\;{{ = }}\;\dfrac{{{{ - (2 + }}\sqrt {{3}} {{)}}}}{{{{(2}}\sqrt {{3}} {{ - 1)}}}}$

केस 1: ${{{m}}_{{2}}}\;{{ = }}\;\dfrac{{{{2 - }}\sqrt {{3}} }}{{{{2}}\sqrt {{3}} {{ + 1}}}}$

बिन्दु ${{(2,3)}}$ से गुजरने वाली रेखा का समीकरण और ढलान $\dfrac{{{{2 - }}\sqrt {{3}} }}{{{{2}}\sqrt {{3}} {{ + 1}}}}$ का होना है।

${{(y - 3)}}\;{{ = }}\;\dfrac{{{{2 - }}\sqrt {{3}} }}{{{{2}}\sqrt {{3}} {{ + 1}}}}{{(x - 2)}}$

$\Rightarrow \;{{(y - 3)(2}}\sqrt {{3}} {{ + 1)}}\;{{ = }}\;{{(2 - }}\sqrt {{3}} {{)x - (2 - }}\sqrt {{3}} {{)2}}$

$\Rightarrow \;{{(2 - }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ + 1)y}}\;{{ = }}\;{{ - 4 + 2}}\sqrt {{3}} {{ + 6}}\sqrt {{3}} {{ + 3}}$

$\Rightarrow \;{{(2 - }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ + 1)y}}\;{{ = }}\;{{ - 1 + 8}}\sqrt {{3}}$

इस स्थिति मे, दूसरी रेखा का समीकरण ${{(2 - }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ + 1)y}}\;{{ = }}\;{{ - 1 + 8}}\sqrt {{3}}$ है 

केस 2 : ${{{m}}_{{2}}}\;{{ = }}\;\dfrac{{{{ - (2 + }}\sqrt {{3}} )}}{{{{2}}\sqrt {{3}} {{ - 1}}}}$

बिन्दु ${{(2,3)}}$ से गुजरने वाली रेखा का समीकरण और ढलान $\dfrac{{{{ - (2 + }}\sqrt {{3}} )}}{{{{2}}\sqrt {{3}} {{ - 1}}}}$ का होना है।

${{(y - 3)}}\;{{ = }}\;\dfrac{{{{ - (2 + }}\sqrt {{3}} {{)}}}}{{{{(2}}\sqrt {{3}} {{ - 1)}}}}{{(x - 2)}}$

$\Rightarrow \;{{(y - 3)(2}}\sqrt {{3}} {{ - 1)}}\;{{ = }}\;{{ - (2 + }}\sqrt {{3}} {{)x + (2 + }}\sqrt {{3}} {{)2}}$

$\Rightarrow \;{{(2 + }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ - 1)y}}\;{{ = }}\;{{4 + 2}}\sqrt {{3}} {{ + 6}}\sqrt {{3}} {{ - 3}}$

$\Rightarrow \;{{(2 + }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ - 1)y}}\;{{ = }}\;{{1 + 8}}\sqrt {{3}}$

इस स्थिति मे, दूसरी रेखा का समीकरण ${{(2 + }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ - 1)y}}\;{{ = }}\;{{1 + 8}}\sqrt {{3}}$ है 

इस प्रकार दूसरी रेखा का आवश्यक समीकरण ${{(2 - }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ + 1)y}}\;{{ = }}\;{{ - 1 + 8}}\sqrt {{3}}$ , ${{(2 + }}\sqrt {{3}} {{)x + (2}}\sqrt {{3}} {{ - 1)y}}\;{{ = }}\;{{1 + 8}}\sqrt {{3}}$

13. बिन्दुओ $(3,4)$ और $( - 1,2)$ को मिलने वाली रेखा खंड के लम्ब संदिवभाजक रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: एक रेखा खंड का दाया दिवभाजक $90^\circ$ पर रेखा खंड को दिवभाजित करता है 

रेखा खंड के अंतिम बिन्दु A, B क्रमश: $(3,4)$ और $( - 1,2)$ के रूप मे दिए गए है 

तदनुसार, AB का मध्य- बिन्दु $\left( {\dfrac{{3 - 10}}{2},\dfrac{{4 + 2}}{0}} \right)$

AB की ढलान, $- \dfrac{{2 - 4}}{{ - 1 - 3}}\; = \;\dfrac{{ - 2}}{{ - 4}}\; = \;\dfrac{1}{2}$

AB के लिए लम्बवत रेखा की ढलान = $- \dfrac{1}{{\dfrac{1}{2}}}\; = \; - 2$

$(1,3)$ से होकर गुजरने वाली रेखा का समीकरण और $- 2$ का ढलान है

$\Rightarrow \;{{(y - 3)}}\;{{ = }}\;{{ - 2(x - 1)}}$

$\Rightarrow \;{{y - 3}}\;{{ = }}\;{{ - 2x + 2}}$

$\Rightarrow \;{{2x + y}}\;{{ = }}\;{{5}}$

इस प्रकार रेखा का आवश्यक समीकरण ${{2x + y}}\;{{ = }}\;{{5}}$ है

14. बिन्दु $( - 1,3)$ से रेखा ${{3x - 4y - 16}}\;{{ = }}\;{{0}}$ पर डाले गए लम्ब पाद के निर्देशांक ज्ञात कीजिए। 

उत्तर: आज्ञा देना ${{(a,b)}}$ बिन्दु से लम्बवत के पैर के निर्देशांक $( - 1,3)$ हो ${{3x - 4y - 16}}\;{{ = }}\;{{0}}$ रेखा तक 

रेखा की ढलान $( - 1,3)$ और ${{(a,b)}}$ , ${{{m}}_{{1}}}\;{{ = }}\;\dfrac{{{{b - 3}}}}{{{{a + 1}}}}$ 

रेखा ${{3x - 4y - 16}}\;{{ = }}\;{{0}}$ , ${{y}}\;{{ = }}\;\dfrac{{{3}}}{{{4}}}{{x - 4}}$ की ढलान ${{{m}}_2}\; = \;\dfrac{3}{4}$

चूंकि ये दोनों रेखाए लम्बवत है, ${{{m}}_1}{{{m}}_2}\; = \; - 1$

$\therefore \;\dfrac{{{{b - 3}}}}{{{{a + 1}}}}{{ \times }}\dfrac{{{3}}}{{{4}}}\;{{ = }}\;{{ - 1 }} \Rightarrow \;\dfrac{{{{3b - 9}}}}{{{{4a + 4}}}}\;{{ = }}\;{{ - 1}}$

$\Rightarrow \;{{3b - 9}}\;{{ = }}\;{{ - 4a - 4}}$

$\Rightarrow \;{{4a + 3b}}\;{{ = }}\;{{5}}$

बिन्दु ${{(a,b)}}$ रेखा पर स्थित ${{3x - 4y - 16}}\;{{ = }}\;{{0}}$

$\therefore \;{{3a - 4b - 16}}\;{{ = }}\;{{0}}$

हम प्राप्त करते है ${{a}}\;{{ = }}\;\dfrac{{{{68}}}}{{{{25}}}}{{,}}\;{{b}}\;{{ = }}\;{{ - }}\dfrac{{{{49}}}}{{{{25}}}}$

इस प्रकार, लम्ब के पैर के आवश्यक निर्देशांक है $(\dfrac{{{{68}}}}{{{{25}}}}{{,}}\;{{ - }}\dfrac{{{{49}}}}{{{{25}}}})$

15. मूल बिन्दु से रेखा ${{y}}\;{{ =  mx + c}}\;$ पर डाला गए लम्ब रेखा से बिन्दु ${{( - 1,2)}}$ पर मिलता है। ${{m, c}}$ का मान ज्ञात कीजिए। 

उत्तर: रेखा का दिया गया समीकरण है ${{y}}\;{{ =  mx + c}}\;$

यह दिया जाता है कि मूल से लम्बवत दी गई रेखा से ${{( - 1,2)}}$ पे मिलती है 

इसलिए बिन्दुओ $(0,0),\;( - 1,2)$ को मिलने वाली रेखा की ढलान = $\dfrac{2}{{ - 1}}\; = \; - 2$

दी गई रेखा की ढलान है ${{m}}$ ,

$\therefore \;{{m}} \times  - 2\; = \; - 1\; \Rightarrow \;{{m}}\;{{ = }}\;\dfrac{1}{2}$

चूंकि बिन्दुओ ${{( - 1,2)}}$ दी गई रेखा पर स्थित है यह ${{y}}\;{{ =  mx + c}}\;$ समीकरण को संतुष्ट करता है 

$\therefore \;{{m(}} - 1) + {{c}}$

$\Rightarrow \;{{2}}\;{{ = }}\;{{2 + }}\dfrac{{{1}}}{{{2}}}{{( - 1) + c}} \Rightarrow \;{{c}}\;{{ = }}\;{{2 + }}\dfrac{{{1}}}{{{2}}}\;{{ = }}\;\dfrac{{{5}}}{{{2}}}$

तथा इस प्रकार ${{m}}$ और ${{c}}$ के संबंधित मूल्य $\dfrac{1}{2},\;\dfrac{5}{2}$ है।

16. यदि ${{p, q}}$ क्रमश: मूल बिन्दु से रेखाओ ${{xcos\theta  - ysin\theta }}\;{{ = }}\;{{kcos\theta }}$ और ${{xsec\theta  + ycosec\theta }}\;{{ = }}\;{{k}}$ पर लम्ब की लम्बाइया है तो सिद्ध कीजिए कि ${{{p}}^{{2}}}{{ + 4}}{{{q}}^{{2}}}\;{{ = }}\;{{{k}}^{{2}}}$

उत्तर: दी गई लाइनों के समीकरण है 

${{xcos\theta  - ysin\theta }}\;{{ = }}\;{{kcos\theta }}$ ..........(1)

${{xsec\theta  + ycosec\theta }}\;{{ = }}\;{{k}}$ ..............(2)

एक रेखा ${{A + B + C}}\;{{ = }}\;{{0}}$ की लम्बवत दूरी ${{d}}$ एक बिन्दु ${{(}}{{{x}}_2}{{,}}{{{y}}_2}{{)}}$ से दिया गया है 

${{d}}\;{{ = }}\;\dfrac{{\left| {{{A}}{{{x}}_{{1}}}{{ + B}}{{{y}}_{{1}}}{{ + C}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

यानि, हम प्राप्त करते है समीकरण के सामान्य समीकरण और समीकरण (1) की तुलना करने पर 

${{A  =  cos\theta , B  =   - sin\theta , C  =   - kcos2\theta }}$

यह दिया जाता है कि ${{p}}$ लम्बवत से रेखा की लंबाई है ${{(0,0)}}$ से रेखा (1) तक 

$\therefore \;{{p}}\;{{ = }}\;\dfrac{{{{|A(0) + B(0) + C|}}}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{|C|}}}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

${{ = }}\;\dfrac{{{{| - kcos2\theta |}}}}{{\sqrt {{{{{(cos\theta )}}}^{{2}}}{{ + ( - sin\theta }}{{{)}}^{{2}}}} }}\;{{ = }}\;{{| - kcos2\theta |}}$ ............(3)

हम प्राप्त करते है सामान्य समीकरण के समीकरण (2) की तुलना करने पर 

${{A  =  sec\theta , B  =  cosec\theta , C  =   - k}}$

यह दिया जाता है कि q लम्बवत ${{(0,0)}}$ से रेखा (2) तक लम्बवत की लंबाई है 

$\therefore \;{{q}}\;{{ = }}\;\dfrac{{{{|A(0) + B(0) + C|}}}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{|C|}}}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

${{ = }}\;\dfrac{{{{| - k|}}}}{{\sqrt {{{{{(sec\theta )}}}^{{2}}}{{ + (cosec\theta }}{{{)}}^{{2}}}} }}$ ..........(4)

समीकरण (3) और (4) हमारे पास है

${{{p}}^{{2}}}{{ + 4}}{{{q}}^{{2}}}\;{{ = }}\;{{| - kcos2\theta }}{{{|}}^{{2}}}{{ + 4}}{\left( {\dfrac{{{{| - k|}}}}{{\sqrt {{{{{(sec\theta )}}}^{{2}}}{{ + (cosec\theta }}{{{)}}^{{2}}}} }}} \right)^{{2}}}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}\dfrac{{{{4}}{{{k}}^{{2}}}}}{{\left( {{{se}}{{{c}}^{{2}}}{{\theta  + cose}}{{{c}}^{{2}}}{{\theta }}} \right)}}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}\dfrac{{{{4}}{{{k}}^{{2}}}}}{{\left( {\dfrac{{{1}}}{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{ + }}\dfrac{{{1}}}{{{{si}}{{{n}}^{{2}}}{{\theta }}}}} \right)}}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}\dfrac{{{{4}}{{{k}}^{{2}}}}}{{\left( {\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta  + co}}{{{s}}^{{2}}}{{\theta }}}}{{{{si}}{{{n}}^{{2}}}{{\theta co}}{{{s}}^{{2}}}{{\theta }}}}} \right)}}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}\dfrac{{{{4}}{{{k}}^{{2}}}}}{{\left( {\dfrac{{{1}}}{{{{si}}{{{n}}^{{2}}}{{\theta co}}{{{s}}^{{2}}}{{\theta }}}}} \right)}}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + 4}}{{{k}}^{{2}}}{{si}}{{{n}}^{{2}}}{{\theta co}}{{{s}}^{{2}}}{{\theta }}$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}{{{k}}^{{2}}}\left( {{{2si}}{{{n}}^{{2}}}{{\theta co}}{{{s}}^{{2}}}{{\theta }}} \right)$

$\Rightarrow \;{{{k}}^{{2}}}{{co}}{{{s}}^{{2}}}{{2\theta  + }}{{{k}}^{{2}}}{{si}}{{{n}}^{{2}}}{{2\theta }}$

$\Rightarrow \;{{{k}}^{{2}}}\left( {{{co}}{{{s}}^{{2}}}{{2\theta  + si}}{{{n}}^{{2}}}{{2\theta }}} \right)$

$\Rightarrow \;{{{k}}^{{2}}}$

इसलिए हमने यह कर दिखाया ${{{p}}^{{2}}}{{ + 4}}{{{q}}^{{2}}}\;{{ = }}\;{{{k}}^{{2}}}$

17. शीर्षों A ${{(2,3)}}$ , B ${{(4, - 1)}}$ और C ${{(1,2)}}$ वाले त्रिभुज ABC के शीर्ष A से उसकी सम्मुख भुजा पर लम्ब डाला गया है। लम्ब की लंबाई तथा समीकरण ज्ञात कीजिए। 

उत्तर: त्रिभुज ABC की ऊंचाई शीर्ष A से AD हो 

${{(2,3)}}$ से होकर गुजरने वाली रेखा का समीकरण और एक का ढलान है 

${{(y - 3)}}\;{{ = }}\;{{1(x - 2)}}$

$\Rightarrow \;{{x - y + 1}}\;{{ = }}\;{{0}}$

$\Rightarrow \;{{y - x}}\;{{ = 1}}\;$ 

शीर्ष से उचाई का समीकरण A = ${{y - x}}\;{{ = 1}}\;$

AD की लंबाई = लम्बवत की लंबाई A ${{(2,3)}}$ से BC तक 

${{(y + 1)}}\;{{ = }}\;\dfrac{{{{2 + 1}}}}{{{{1 - 4}}}}{{(x - 4)}}$

$\Rightarrow \;{{(y + 1)}}\;{{ = }}\;{{ - 1(x - 4)}}$

$\Rightarrow \;{{y + 1 = }}\;{{ - x + 4}}$

$\Rightarrow \;{{x + y - 3}}\;{{ = }}\;{{0}}$ ..........(1)

एक बिन्दु ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ से एक रेखा की लम्बवत दूरी ${{d}}$ , ${{Ax + By + C}}\;{{ = }}\;{{0}}$ से दी जाती है 

${{d}}\;{{ = }}\;\dfrac{{\left| {{{A}}{{{x}}_{{1}}}{{ + B}}{{{y}}_{{1}}}{{ + C}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

सामान्य समीकरण की तुलना समीकरण (1) से करने पर हम ${{A  =  1, B  =  1, C  =   - 3}}$ प्राप्त करते है 

AD की लंबाई = ${{ = }}\;\dfrac{{{{|1 \times 2 + 1 \times 3 - 3|}}}}{{\sqrt {{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}} }}\;{{ = }}\;\dfrac{{{{|2|}}}}{{\sqrt {{2}} }}\;{{ = }}\;\dfrac{{{2}}}{{\sqrt {{2}} }}\;{{ = }}\sqrt {{2}}$

इस प्रकार शीर्ष A से उचाई के समीकरण ${{y - x}}\;{{ = 1}}\;$ और लंबाई $\sqrt {{2}}$ इकाइया है।

18. यदि ${{p}}$ मूल बिन्दु से उस रेखा पर डाले लम्ब की लंबाई हो जिस पर अक्षों पर कटे अतः खंड ${{a, b}}$ हो, तो दिखाइए कि $\dfrac{{{1}}}{{{{{p}}^{{2}}}}}\;{{ = }}\;\dfrac{{{1}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{1}}}{{{{{b}}^{{2}}}}}$

उत्तर: यह ज्ञात है कि एक रेखा का समीकरण जिसका अक्षों पर खंड है ${{a,}}\;{{b }}$ है

$\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}\;{{ = }}\;{{1}}$

$\Rightarrow \;{{bx + ay}}\;{{ = }}\;{{ab}}$

$\Rightarrow \;{{bx + ay - ab}}\;{{ = }}\;{{0 }}$ ............(1)

बिन्दु ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ से एक रेखा ${{Ax + By + C}}\;{{ = }}\;{{0}}$ की लम्बवत दूरी ${{d}}$ दी गई है। 

${{d}}\;{{ = }}\;\dfrac{{\left| {{{A}}{{{x}}_{{1}}}{{ + B}}{{{y}}_{{1}}}{{ + C}}} \right|}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

समीकरण (1) की तुलना सामान्य समीकरण ${{Ax + By + C}}\;{{ = }}\;{{0}}$ से करने पर ${{A  =  b, B  =  a, C  =   - ab}}$

इसलिए, यदि बिन्दु $(0,0)$ से रेखा (1) तक लम्ब की लंबाई ${{p}}$ है, हमने प्राप्त किया

${{p}}\;{{ = }}\;\dfrac{{{{|A(0) + B(0) + C|}}}}{{\sqrt {{{{A}}^{{2}}}{{ + }}{{{B}}^{{2}}}} }}$

$\Rightarrow \;{{p}}\;{{ = }}\;\dfrac{{{{| - ab|}}}}{{\sqrt {{{{b}}^{{2}}}{{ + }}{{{a}}^{{2}}}} }}$

$\Rightarrow \;{{{p}}^{{2}}}\;{{ = }}\;\dfrac{{{{{{( - ab)}}}^{{2}}}}}{{{{{a}}^{{2}}}{{ + }}{{{b}}^{{2}}}}}$

$\Rightarrow \;{{{p}}^{{2}}}\left( {{{{a}}^{{2}}}{{ + }}{{{b}}^{{2}}}} \right)\;{{ = }}\;{{{a}}^{{2}}}{{{b}}^{{2}}}$

$\Rightarrow \;\dfrac{{\left( {{{{a}}^{{2}}}{{ + }}{{{b}}^{{2}}}} \right)}}{{{{{a}}^{{2}}}{{{b}}^{{2}}}}}\;{{ = }}\;\dfrac{{{1}}}{{{{{p}}^{{2}}}}}$

$\Rightarrow \;\dfrac{{{1}}}{{{{{p}}^{{2}}}}}{{ = }}\;\dfrac{{{1}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{1}}}{{{{{b}}^{{2}}}}}$ 

इसलिए हमने यह कर दिखाया $\dfrac{{{1}}}{{{{{p}}^{{2}}}}}\;{{ = }}\;\dfrac{{{1}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{1}}}{{{{{b}}^{{2}}}}}$

प्रश्नावली A10

1. ${{k}}$ का मान ज्ञात कीजिए जबकि रेखा ${{(k - 3)x - (4 - }}{{{k}}^{{2}}}{{)y + }}{{{k}}^{{2}}}{{ - 7k + 6}}\;{{ = }}\;{{0}}$ 

(a) ${{x}}$ - अक्ष के समांतर है। 

उत्तर: ${{x}}$ - अक्ष के समांतर का समीकरण होगा ${{y  =  a}}$

${{x}}$ का गुणांक = ${{0 }}$

$\Rightarrow \;{{k - 3  = }}\;{{0 }} \Rightarrow \;{{k  =  3}}$

(b) ${{y}}$ - अक्ष के समांतर है। 

उत्तर: ${{y}}$ - अक्ष के समांतर का समीकरण होगा ${{x  =  a}}$ 

${{y}}$ का गुणांक = ${{0 }}$

$\Rightarrow \;4 - {{{k}}^2}{{  = }}\;{{0 }} \Rightarrow \;{{{k}}^2}{{  =  4 }}\; \Rightarrow \;{{k}}\;{{ = }}\;{{ \pm 2}}$

(c) मूल बिन्दु से जाती है 

उत्तर: मूल बिन्दु से जाती रेखा को निर्देशांक $(0,0)$ संतुष्ट करेगा

${{0 + 0 + }}{{{k}}^{{2}}}{{ - 7k + 6}}\;{{ = }}\;{{0}}$

${{{k}}^{{2}}}{{ - 7k + 6}}\;{{ = }}\;{{0}}$

${{{k}}^{{2}}}{{ - 6k - k + 6}}\;{{ = }}\;{{0}}$

${{(k - 6)(k - 1)}}\;{{ = }}\;{{0}}$

${{k}}\;{{ = }}\;{{6,}}\;{{k}}\;{{ = }}\;{{1}}$

2. ${{\theta ,}}\;{{p }}$ के मान ज्ञात कीजिए यदि समीकरण ${{xcos}}\theta {{ + ysin}}\theta \;{{ = }}\;{{p }}$ रेखा $\sqrt {{3}} {{x + y + 2}}\;{{ = }}\;{{0}}$ का लम्ब रूप है। 

उत्तर: दिया गया है $\sqrt {{3}} {{x + y + 2}}\;{{ = }}\;{{0}}$ $\Rightarrow \;{{ - }}\sqrt {{3}} {{x - y}}\;{{ = }}\;{{2}}$

दोनों तरफ $\sqrt {{{{{( - }}\sqrt {{3}} {{)}}}^2} + {{( - 1)}^2}} \; = \;2$ से भाग करने पर, हमे प्राप्त होगा

${{ - }}\dfrac{{\sqrt {{3}} }}{{{2}}}{{x - }}\dfrac{{{1}}}{{{2}}}{{y}}\;{{ = }}\;{{1}}$ ..........(1)

दिया गया है ${{xcos}}\theta {{ + ysin}}\theta \;{{ = }}\;{{p }}$ .........(2)

समीकरण (1) और (2) की तुलना करने पर हमे मिलेगा 

${{cos\theta }}\;{{ = }}\;{{ - }}\dfrac{{\sqrt {{3}} }}{{{2}}}{{,}}\;{{sin\theta }}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{{2}}}{{,}}\;{{p}}\;{{ = }}\;{{1}}$

${{sin\theta }}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{{2}}}$

${{sin\theta }}\;{{ = }}\;\sin (\pi  + \dfrac{\pi}{6})\; \Rightarrow \;\theta \; = \;\dfrac{{7\pi }}{6}$

3. उन रेखाओ के समीकरण ज्ञात कीजिए जिनके अक्षों से कटे अतः खंडों का योग और गुणनफल क्रमश: ${{1,}}\;{{ - 6 }}$ है

उत्तर: मान लेते है कि अक्षों से कटे अतः खंड ${{a,}}\;{{b}}$

दिया गया है ${{a + b}}\;{{ = }}\;{{1,}}\;{{ab}}\; = \; - 6$

$\Rightarrow \;{{b = }}\;{{1 - a}}$

$\Rightarrow \;{{a - }}{{{a}}^{{2}}}\;{{ = }}\;{{ - 6}}$

$\Rightarrow {{{a}}^{{2}}}{{ - a - 6}}\;{{ = }}\;{{0}}$

$\Rightarrow {{{a}}^{{2}}}{{ - 3a + 2a - 6}}\;{{ = }}\;{{0}}$

$\Rightarrow \;{{(a - 3)(a + 2)}}\;{{ = }}\;{{0}}$

$\Rightarrow {{a  =  3, a  =   - 2}}$

$\therefore \;{{b}}\;{{1 - 3}}\;{{ = }}\;{{ - 2, b  =  1 + 2  =  3}}$

$\Rightarrow \;{{b  =   - 2,3 }}$

$(3, - 2)$ अतः खंड वाली रेखा का समीकरण होगा 

$\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{{ - 2}}}}\;{{ = }}\;{{1}}\; \Rightarrow \;{{2x + 3y - 6}}\;{{ = }}\;{{0}}$

$(2, - 1)$ अतः खंड वाली रेखा का समीकरण होगा 

$\dfrac{{{x}}}{{ - 2}}{{ + }}\dfrac{{{y}}}{3}\;{{ = }}\;{{1}}\; \Rightarrow \;3{{x - 2y + 6}}\;{{ = }}\;{{0}}$

4.  ${{y}}$ - अक्ष पर कौन से बिन्दु ऐसे है, जिनकी रेखा $\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{4}}}\;{{ = }}\;{{1}}$ से दूरी इकाई है। 

उत्तर: मान लेते है कि ${{y}}$ - अक्ष पर बिन्दु के निर्देशांक ${{(0,y)}}$ है 

 $\dfrac{{{x}}}{{{3}}}{{ + }}\dfrac{{{y}}}{{{4}}}\;{{ = }}\;{{1}}$ $\Rightarrow \;4{{x + 3y}}\;{{ = }}\;12$

रेखा $4{{x + 3y}}\;{{ = }}\;12$ की ${{(0,y)}}$ दूरी होगी 

$\Rightarrow \;\dfrac{{4 \times 0{{ + 3y - }}12}}{{\sqrt {{4^2} + {3^2}} }}\; = \;4\; \Rightarrow \;\dfrac{{{{3y - 12}}}}{{{5}}}\;{{ = }}\;{{ \pm 4}}$

i. $\dfrac{{{{3y - 12}}}}{{{5}}}\;{{ = }}\;{{4}}\; \Rightarrow \;3{{y}}\;{{ = }}\;32\; \Rightarrow \;{{y}}\; = \;\dfrac{{32}}{3}$

ii. $\dfrac{{{{3y - 12}}}}{{{5}}}\;{{ = }}\; - {{4}}\; \Rightarrow \;3{{y}}\;{{ = }}\; - 8\; \Rightarrow \;{{y}}\; = \;\dfrac{{ - 8}}{3}$

${{y}}$ - अक्ष पर बिन्दु जिनकी दूरी चार इकाई है होंगे: $(0,\dfrac{{32}}{3}),\;(0,\dfrac{{ - 8}}{3})$

5. मूल बिन्दुओ ${{(cos}}\theta {{,}}\;{{sin}}\theta {{),}}\;{{(cos}}\emptyset {{,}}\;{{sin}}\emptyset {{) }}$ को मिलने वाली रेखा की लांबिक दूरी ज्ञात कीजिए। 

उत्तर: ${{(cos}}\theta {{,}}\;{{sin}}\theta {{),}}\;{{(cos}}\emptyset {{,}}\;{{sin}}\emptyset {{) }}$ को मिलने वाली रेखा का समीकरण है

$\left( {{{y - }}{{{y}}_{{1}}}} \right)\;{{ = }}\;\dfrac{{\left( {{{{y}}_{{2}}}{{ - }}{{{y}}_{{1}}}} \right)}}{{\left( {{{{x}}_{{2}}}{{ - }}{{{x}}_{{1}}}} \right)}}\left( {{{x - }}{{{x}}_{{1}}}} \right){{(y - sin\theta )}}\;$

$= \;\dfrac{{(\sin \emptyset  - \sin \theta )}}{{(\cos \emptyset  - \cos \theta )}}{{(x - cos\theta )}}$

$= \;\dfrac{{2\cos \left( {\dfrac{{\theta  + \theta }}{2}} \right)\sin \left( {\dfrac{{\emptyset  - \theta }}{2}} \right)}}{{ - 2\sin \left( {\dfrac{{\theta  + \theta }}{2}} \right)\sin \left( {\dfrac{{\emptyset  - \theta }}{2}} \right)}}\; = \; - \dfrac{{\cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)}}{{\sin \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)}}(x - \cos \theta )$

$\Rightarrow \;({{y}} - \sin \theta )\sin \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)\; = \; - ({{x}} - \cos \theta )\cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)$

$\Rightarrow \;{{x}}\cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right) + {{y}}\sin \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)\; = \;\cos \theta \cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right) + \sin \theta \sin \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)\;$

$= \;\cos \left( {\theta  - \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)} \right)$

${{x}}\cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right) + {{y}}\sin \left( {\dfrac{{\emptyset  + \theta }}{2}} \right)\; = \;\cos \left( {\dfrac{{\theta  - \emptyset }}{2}} \right)$

मूल बिन्दुओ से रेखा की दूरी = $\dfrac{{\cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right) \times 0 + \cos \left( {\dfrac{{\emptyset  + \theta }}{2}} \right) \times 0 - \cos \left( {\dfrac{{\theta  - \emptyset }}{2}} \right)}}{{\sqrt {\cos {{\left( {\dfrac{{\emptyset  + \theta }}{2}} \right)}^2} + \sin {{\left( {\dfrac{{\emptyset  + \theta }}{2}} \right)}^2}} }}\; = \;\cos \left( {\dfrac{{\theta  - \emptyset }}{2}} \right)$

6. रेखाओ ${{x - 7y + 5}}\;{{ = }}\;{{0,}}\;{{3x + y}}\;{{ = }}\;{{0}}$ के प्रतिच्छेद बिन्दु से खींची गई और ${{y}}$ - अक्ष के समांतर रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: दिया गया है 

${{x - 7y + 5}}\;{{ = }}\;{{0}}$ ..............(1)

${{3x + y}}\;{{ = }}\;{{0}}$ ........ (2)

अतः समीकरण (1) और (2) हल करने पर हमे मिलेगा, ${{x}}\;{{ = }}\;{{ - }}\dfrac{{{5}}}{{{{22}}}}{{,}}\;{{y}}\;{{ = }}\;{{ - }}\dfrac{{{{15}}}}{{{{22}}}}$

रेखाओ ${{x - 7y + 5}}\;{{ = }}\;{{0,}}\;{{3x + y}}\;{{ = }}\;{{0}}$ का प्रतिच्छेद बिन्दु है, ${{( - }}\dfrac{{{5}}}{{{{22}}}}{{, - }}\dfrac{{{{15}}}}{{{{22}}}})$

${{( - }}\dfrac{{{5}}}{{{{22}}}}{{, - }}\dfrac{{{{15}}}}{{{{22}}}})$ से होकर जाने वाली और ${{y}}$ - अक्ष के समांतर रेखा के लिए ${{y}}\;{{ = }}\;{{0 }}$ होगा। अतः उस रेखा का समीकरण होगा, ${{x  =   - }}\dfrac{{{5}}}{{{{22}}}}\; \Rightarrow \;{{22x + 5}}\;{{ = }}\;{{0}}$

7. रेखा $\dfrac{{{x}}}{4}{{ + }}\dfrac{{{y}}}{6}\;{{ = }}\;{{1}}$ पर लम्ब उस बिन्दु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहा यह रेखा ${{y}}$ - अक्ष से मिलती है। 

उत्तर: दिया गया है $\dfrac{{{x}}}{4}{{ + }}\dfrac{{{y}}}{6}\;{{ = }}\;{{1}}$ $\Rightarrow \;3{{x + 2y}}\;{{ = }}\;12$ $\Rightarrow \;{{y}}\;{{ = }}\;{{ - }}\dfrac{3}{2}x + 6$

अतः दी गई रेखा की ढाल = ${{ - }}\dfrac{3}{2}$

रेखा $\dfrac{{{x}}}{4}{{ + }}\dfrac{{{y}}}{6}\;{{ = }}\;{{1}}$ और उस रेखा पर लम्ब उस बिन्दु से खींची गई रेखा के बीच मे ${{90}}^\circ$ का कोण होगा 

दूसरी रेखा की ढाल = $- 1 \times ( - \dfrac{2}{3})\; = \;\dfrac{2}{3}$

चूंकि यह रेखा ${{y}}$ - अक्ष पर प्रतिच्छेद करती है, अतः यह $(0,6)$ से जाएगी, अतः इसका समीकरण होगा 

${{(y - 6)}}\;{{ = }}\;\dfrac{{{2}}}{{{3}}}{{(x - 0)}}$ $\Rightarrow \;{{2x - 3y + 18}}\;{{ = }}\;{{0}}$

8. रेखाओ ${{y - x}}\;{{ = }}\;{{0,}}\;{{x + y}}\;{{ = }}\;{{0,}}\;{{x - k}}\;{{ = }}\;{{0}}$ से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए। 

उत्तर: दिया गया है 

${{y - x}}\;{{ = }}\;{{0}}$ ............(1)

${{x + y}}\;{{ = }}\;{{0}}$ ..............(2)

${{x - k}}\;{{ = }}\;{{0}}$ ............(3)

रेखाओ (1) और (2) का प्रतिच्छेद बिन्दु होगा $(0,0)$

रेखाओ (2) और (3) का प्रतिच्छेद बिन्दु होगा ${{(k, - k)}}$

रेखाओ (3) और (1) का प्रतिच्छेद बिन्दु होगा ${{(k,k)}}$

हमे ज्ञात है कि एक त्रिभुज का क्षेत्रफल = $\dfrac{1}{2}\mid {{{x}}_1}\left( {{{{y}}_2} - {{{y}}_3}} \right) + {{{x}}_2}\left( {{{{y}}_3} - {{{y}}_1}} \right) + {{{x}}_3}\left( {{{{y}}_1} - {{{y}}_2}} \right)\mid$
$= \;\dfrac{1}{2}|0 \times ( - {{k}} - {{k}}) + {{k}}({{k}} - 0) + {{k}}(0 + {{k}})|$

$= \;\dfrac{1}{2}\left| {2{{{k}}^2}} \right|\; = \;{{{k}}^2}$

9. ${{p}}$ का मान ज्ञात कीजिए जिसमे तीन रेखाए ${{3x + y  - 2 }}\;{{ = }}\;{{0,}}\;{{px + 2y}}\;{{ = }}\;{{3,}}\;{{2x - y - 3}}\;{{ = }}\;{{0  }}$ एक बिन्दु पर प्रतिच्छेद करे। 

उत्तर: दिया गया है तीन रेखाए ${{3x + y  - 2 }}\;{{ = }}\;{{0,}}\;{{px + 2y}}\;{{ = }}\;{{3,}}\;{{2x - y - 3}}\;{{ = }}\;{{0  }}$ एक बिन्दु पर प्रतिच्छेद कर रही है 

${{3x + y  - 2 }}\;{{ = }}\;{{0}}$ ............(1)

${{2x - y - 3}}\;{{ = }}\;{{0  }}$ ..............(2)

समीकरण (1) और (2) को हल करने पर हमे मिलेगा ${{x  = }}\;{{1,}}\;{{y  = }}\;{{ - 1 }}$

अतः रेख (1) और (2), ${{(1, - 1 )}}$ पर प्रतिच्छेद करती है, जिसका अर्थ यह है कि रेखा ${{px + 2y}}\;{{ = }}\;{{3}}$ भी इस बिन्दु से होकर जाएगी। 

${{(1, - 1 )}}$, ${{px + 2y}}\;{{ = }}\;{{3}}$ को संतुष्ट करेगा

$\Rightarrow \;{{p \times 1 + 2 \times ( - 1)}}\;{{ = }}\;{{3}}\; \Rightarrow \;{{p - 2}}\;{{ = }}\;{{3}}$

$\Rightarrow \;{{p}}\;{{ = }}\;{{5}}$

10. यदि तीन रेखाए जिनके समीकरण ${{y}}\;{{ = }}\;{{{m}}_{{1}}}{{x + }}{{{c}}_{{1}}}{{,}}\;{{y}}\;{{ = }}\;{{{m}}_{{2}}}{{x + }}{{{c}}_{{2}}}{{,}}\;{{y}}\;{{ = }}\;{{{m}}_{{3}}}{{x + }}{{{c}}_{{3}}}$ है, संगामी है तो दिखाइए कि ${{{m}}_{{1}}}{{(}}{{{c}}_{{2}}}{{ - }}{{{c}}_{{3}}}{{) + }}{{{m}}_{{2}}}{{(}}{{{c}}_{{3}}}{{ - }}{{{c}}_{{1}}}{{) + }}{{{m}}_{{3}}}{{(}}{{{c}}_{{1}}}{{ - }}{{{c}}_{{2}}}{{)}}\;{{ = }}\;{{0}}$ 

उत्तर: ${{y}}\;{{ = }}\;{{{m}}_{{1}}}{{x + }}{{{c}}_{{1}}}$ .........(1)

${{y}}\;{{ = }}\;{{{m}}_{{2}}}{{x + }}{{{c}}_{{2}}}$ ..........(2)

${{y}}\;{{ = }}\;{{{m}}_{{3}}}{{x + }}{{{c}}_{{3}}}$ ............(3)

समीकरण (1) और (2) को हल करने पर, हमे मिलेगा ${{x}}\; = \;\dfrac{{{{{c}}_2} - {{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}},{{y}}\; = \;\dfrac{{{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}}$

अतः रेखा (1) और (2) $(\dfrac{{{{{c}}_2} - {{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}},\dfrac{{{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}})$ पर प्रतिच्छेद करती है 

दिया गया है कि तीनों रेखे संगामी है, अतः $(\dfrac{{{{{c}}_2} - {{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}},\dfrac{{{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}})$

रेखा (3) को संतुष्ट करेगा

$\therefore \;\dfrac{{{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}}\; = \;{{{m}}_3}\left( {\dfrac{{{{{c}}_2} - {{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}}} \right) + {{{c}}_3}$

 $\Rightarrow \;\dfrac{{{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1}}}{{\;{{{m}}_1} - {{{m}}_2}}}\; = \;\left( {\dfrac{{{{{m}}_3}{{{c}}_2} - {{{m}}_3}{{{c}}_1} + {{{m}}_1}{{{c}}_3} - {{{m}}_2}{{{c}}_3}}}{{\;{{{m}}_1} - {{{m}}_2}}}} \right)$

 $\Rightarrow \;{{{m}}_1}{{{c}}_2} - {{{m}}_2}{{{c}}_1} - {{{m}}_3}{{{c}}_2} + {{{m}}_3}{{{c}}_1} - {{{m}}_1}{{{c}}_3} + {{{m}}_2}{{{c}}_3}\; = \;0$

 $\Rightarrow \;{{{m}}_1}\left( {{{{c}}_2} - {{{c}}_3}} \right) + {{{m}}_2}\left( {{{{c}}_3} - {{{c}}_1}} \right) + {{{m}}_3}\left( {{{{c}}_1} - {{{c}}_2}} \right)\; = \;0$

11. बिन्दु ${{(3,2)}}$ से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो रेखा ${{x - 2y}}\;{{ = }}\;{{3 }}$ से ${{45}}^\circ$ का कोण बनती है। 

उत्तर: दिया गया है $\theta \;{{ = }}\;{{45}}^\circ$

${{x - 2y}}\;{{ = }}\;{{3 }}$ $\Rightarrow \;{{y}}\;{{ = }}\;\dfrac{{{1}}}{{{2}}}{{x - }}\dfrac{{{3}}}{{{2}}}$

$\Rightarrow \;{{m}}\;{{ = }}\;\dfrac{{{1}}}{{{2}}}$

हमे ज्ञात है कि $\pm \tan \theta \; = \;\dfrac{{{{{m}}_2} - {{{m}}_1}}}{{1 + {{{m}}_1}\;{{{m}}_2}}}$

$\Rightarrow \;{{ \pm tan4}}{{{5}}^{{^\circ }}}\;{{ = }}\;\dfrac{{{{{m}}_{{2}}}{{ - }}\dfrac{{{1}}}{{{2}}}}}{{{{1 + }}{{{m}}_{{2}}}{{ \times }}\dfrac{{{1}}}{{{2}}}}}\;{{ = }}\;\dfrac{{{{2}}{{{m}}_{{2}}}{{ - 1}}}}{{{{2 + }}{{{m}}_{{2}}}}}$

$\Rightarrow {{ \pm 1}}\;{{ = }}\;\dfrac{{{{2}}{{{m}}_{{2}}}{{ - 1}}}}{{{{2 + }}{{{m}}_{{2}}}}}$
(i) $1\; = \;\dfrac{{2\;{{{m}}_2} - 1}}{{2 + {{{m}}_2}}}$

$\Rightarrow \;2 + {{{m}}_2}\; = \;2\;{{{m}}_2} - 1$

$\Rightarrow \;{{{m}}_2}\; = \;3$

(ii) $ - 1\; = \;\dfrac{{2\;{{{m}}_2} - 1}}{{2 + {{{m}}_2}}}\;$

$\Rightarrow \; - 2 - {{{m}}_2}\; = \;2\;{{{m}}_2} - 1$

$\Rightarrow \;{{{m}}_2}\; = \; - \dfrac{1}{3}$

12. रेखाओ ${{4x + 7y - 3}}\;{{ = }}\;{{0,}}\;{{2x - 3y + 1}}\;{{ = }}\;{{0}}$ के प्रतिच्छेद बिन्दु से जाने वाली रेखा का समीकरण ज्ञात कीजिए जो अक्षों से समान अतः खंड बनती है। 

उत्तर: उस रेखा का समीकरण जो अक्षों से समान अतः खंड बनती है होगा 

$\dfrac{{{x}}}{{{a}}}{{ + }}\dfrac{{{y}}}{{{b}}}\;{{ = }}\;{{1}}\; \Rightarrow \;{{x + y}}\;{{ = }}\;{{a}}$ ........(1)

${{4x + 7y - 3}}\;{{ = }}\;0$ .........(2)

${{2x - 3y + 1 }}\;{{ = }}\;0$ ..........(3)

अतः समीकरण (1),(2) को हल करने पर हमे मिलेगा ${{x}}\;{{ = }}\;\dfrac{{{1}}}{{{{13}}}}{{,y}}\;{{ = }}\;\dfrac{{{5}}}{{{{13}}}}$

${{x,y}}$ का मान समीकरण (1) पर रखने से हमे मिलेगा

$\dfrac{1}{{13}} + \dfrac{5}{{13}}\; = \;{{a}}$

$\Rightarrow \;{{a}}\; = \;\dfrac{6}{{13}} \Rightarrow \;{{x}} + {{y}}\; = \;\dfrac{6}{{13}}$

$\Rightarrow \;13{{x}} + 13{{y}} - 6\; = \;0$

13. दर्शाइए कि मूल बिन्दु से जाने वाली और रेखा ${{y}}\;{{ = }}\;{{mx + c}}$ से $\theta$ कोण बनाने वाली उस रेखा का समीकरण $\dfrac{{{y}}}{{{x}}}\;{{ = }}\;{{ \pm }}\dfrac{{{{m \pm tan\theta }}}}{{{{1}} \mp {{tan\theta }}}}$ है। 

उत्तर: रेखा $\mathrm{y}=\mathrm{m}^{\prime} \mathrm{x}$, रेखा $\mathrm{y}=\mathrm{mx}+\mathrm{c}$ से $\theta$ कोण बनती है तो $\pm \tan \theta=\dfrac{\mathrm{m}-\mathrm{m}}{1+\mathrm{m}^{\prime} \mathrm{m}}$

(i) $\tan \theta=\dfrac{\mathrm{m}-\mathrm{m}}{1+\mathrm{m} \mathrm{m}}$

$\tan \theta\left(1+\mathrm{m}^{\prime} \mathrm{m}\right)=\mathrm{m}^{\prime}-\mathrm{m}$

$\therefore \mathrm{m}^{\prime}(1-\mathrm{m} \tan \theta)=\mathrm{m}+\tan \theta \Rightarrow \mathrm{m}^{\prime}=\dfrac{\mathrm{m}+\tan \theta}{1-\mathrm{m} \tan \theta}$

(ii) $-\tan \theta=\dfrac{\mathrm{m}-\mathrm{m}^{\prime}}{1+\mathrm{m}^{\prime} \mathrm{m}}$

$-\tan \theta\left(1+\mathrm{m}^{\prime} \mathrm{m}\right)=\mathrm{m}^{\prime}-\mathrm{m}$

$\therefore \mathrm{m}^{\prime}(1+\mathrm{m} \tan \theta)=\mathrm{m}+\tan \theta \Rightarrow \mathrm{m}^{\prime}=\dfrac{\mathrm{m}-\tan \theta}{1-\mathrm{m} \tan \theta}$

$\therefore \mathrm{m}^{\prime}=\dfrac{\mathrm{m} \pm \tan \theta}{1 \mp \mathrm{m} \tan \theta} \mathrm{y}=\mathrm{m}^{\prime} \mathrm{x}$

$\Rightarrow \dfrac{\mathrm{y}}{\mathrm{x}}=\dfrac{\mathrm{m} \pm \tan \theta}{1 \mp \mathrm{m} \tan \theta}$

14. $( - 1,1),\;(5,7)$ को मिलने वाली रेखाखंड को रेखा ${{x + y}}\;{{ = }}\;{{4}}$ किस अनुपद मे विभाजित करती है। 

उत्तर: $( - 1,1),\;(5,7)$ को मिलने वाली रेखाखंड का समीकरण होगा 

${{(y - 1)}}\;{{ = }}\;\dfrac{{{{(7 - 1)}}}}{{{{(5 + 1)}}}}{{(x + 1)}}$

$\Rightarrow \;{{6y - 6  = }}\;{{6x  + 6  }} \Rightarrow \,{{x - y + 2}}\;{{ = }}\;{{0}}$ ........(1)

${{x + y}}\;{{ = }}\;{{4}}$ ..........(2)

समीकरण (1) और (2) को हल करने पर हमे मिलेगा ${{x}}\;{{ = }}\;{{1,}}\;{{y}}\;{{ = }}\;{{3}}$

अतः रेखा (1) और (2), ${{(1,3)}}$ पे प्रतिच्छेद करती है 

मान लेते है कि रेखा ${{x - y + 2}}\;{{ = }}\;{{0}}$ , ${{x + y}}\;{{ = }}\;{{4}}$ को ${{1:k}}$ के अनुपात मे विभाजित करती है

$\therefore \;(1,3)\; = \;\left( {\dfrac{{{{k}}( - 1) + 1(5)}}{{{{k}} + 1}},\dfrac{{{{k}}(1) + 1(7)}}{{{{k}} + 1}}} \right)$

$\therefore \;\dfrac{{ - {{k}} + 5}}{{{{k}} + 1}}\; = \;1\dfrac{{{{k}} + 7}}{{{{k}} + 1}}\; = \;3$

$\therefore \;{{k}} + 1\; = \; - {{k}} + 5$

$\Rightarrow \;2{{k}}\; = \;4\; \Rightarrow \;{{k}}\; = \;2$

तो, रेखा ${{x - y + 2}}\;{{ = }}\;{{0}}$ , ${{x + y}}\;{{ = }}\;{{4}}$ को ${{1:k}}$ के अनुपात मे विभाजित करती है।

15. बिन्दु ${{(1,2)}}$ से रेखा ${{4x + 7y + 5  =  0 }}$ की ${{2x - y}}\;{{ = }}\;0$ के अनुदशी दूरी ज्ञात कीजिए। 

उत्तर: दिया गया है कि ${{4x + 7y + 5  =  0 }}$ ........(1)

${{2x - y}}\;{{ = }}\;0$ ........(2)

समीकरण (1) और (2) को हल करने पर हमे मिलेगा ${{x}}\;{{ = }}\; - \dfrac{5}{{{{18 }}}}{{,y}}\;{{ = }}\; - \dfrac{{{5}}}{9}$

रेखाए (1),(2), $( - \dfrac{5}{{{{18 }}}}{{,}} - \dfrac{{{5}}}{9})$ पर प्रतिच्छेद करती है। 

${{(1,2)}}$ की बिन्दु $( - \dfrac{5}{{{{18 }}}}{{,}} - \dfrac{{{5}}}{9})$ से दूरी = $\sqrt {{{\left( {1 + \dfrac{5}{{18}}} \right)}^2} + {{\left( {1 + \dfrac{5}{9}} \right)}^2}}$

$= \;\sqrt {{{\left( {\dfrac{{23}}{{18}}} \right)}^2} + {{\left( {\dfrac{{14}}{9}} \right)}^2}} \; = \;\dfrac{{23}}{9}\sqrt {\dfrac{5}{4}} \;$

$= \;\dfrac{{23\sqrt 5 }}{{18}}$

16. बिन्दु ${{( - 1,2)}}$ से खींची जा सकने वाली उस रेखा की दिशा ज्ञात कीजिए जिसका रेखा ${{x + y}}\;{{ = }}\;{{4 }}$ से प्रतिच्छेद  बिन्दु दिए गए बिन्दु से ${{3 }}$ इकाई की दूरी पर है 

उत्तर: मान लेते है कि बिन्दु ${{( - 1,2)}}$ से होकर जाने वाली रेखा का समीकरण ${{y  =  mx  + c }}$ है 

${{2}}\;{{ = }}\;{{ - m + c}}\; \Rightarrow \;{{c}}\;{{ = }}\;{{2 + m}}$

${{mx - y + 2 + m}}$ ........(1)

${{x + y}}\;{{ = }}\;{{4 }}$ ........(2)

समीकरण (1),(2) को हल करने पर ${{x}}\;{{ = }}\,\;\dfrac{{{{2 - m}}}}{{{{m + 1}}}}{{,y}}\;{{ = }}\;\dfrac{{{{5m + 2}}}}{{{{m + 1}}}}$

अतः रेखाए (1) और (2) $(\dfrac{{{{2 - m}}}}{{{{m + 1}}}}{{,}}\dfrac{{{{5m + 2}}}}{{{{m + 1}}}})$ पर प्रतिच्छेद करती है 

$(\dfrac{{{{2 - m}}}}{{{{m + 1}}}}{{,}}\dfrac{{{{5m + 2}}}}{{{{m + 1}}}})$ की ${{( - 1,2)}}$ से दूरी = ${{3 }}$

$\therefore \;\sqrt {{{\left( {\dfrac{{2 - {{m}}}}{{{{m}} + 1}} + 1} \right)}^2} + {{\left( {\dfrac{{5\;{{m}} + 2}}{{\;{{m}} + 1}} - 2} \right)}^2}} \; = \;3$

$\Rightarrow \;{\left( {\dfrac{{2 - {{m}}}}{{{{m}} + 1}} + 1} \right)^2} + {\left( {\dfrac{{5\;{{m}} + 2}}{{\;{{m}} + 1}} - 2} \right)^2}\; = \;9$

$\therefore \;{\left( {\dfrac{3}{{\;{{m}} + 1}}} \right)^2} + {\left( {\dfrac{{3\;{{m}}}}{{\;{{m}} + 1}}} \right)^2}\; = \;9 \Rightarrow \;{{{m}}^2} + 1\; = \;{({{m}} + 1)^2}$

$\Rightarrow \;2\;{{m}}\; = \;0 \Rightarrow {{m}}\; = \;0$

कुनकी रेखा की ढाल $0$ है तो रेखा ${{x}}$ - अक्ष के समांतर है।

17. समकोण त्रिभुज के कर्ण के अन्त्य बिन्दु ${{(1,3), ( - 4,1)}}$ है। त्रिभुज के पाद (समकोणीय भुजाओ) का एक समीकरण ज्ञात कीजिए। 

उत्तर: मान लेते है कि त्रिभुज के पाद BC की ढाल ${{m }}$ है 

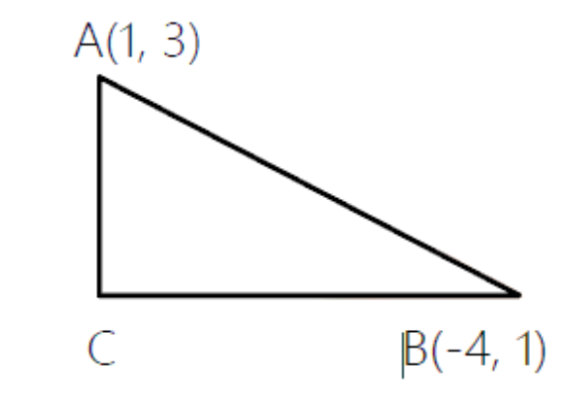
AC की ढाल = ${{ - }}\dfrac{{{1}}}{{{m}}}$

BC का समीकरण, ${{y - 1}}\;{{ = }}\;{{m(x + 4)}} \Rightarrow \;{{mx - y + 4m + 1}}\;{{ = }}\;{{0}}$ ..........(1)

AC का समीकरण, ${{y}} - 3\; = \; - \dfrac{1}{{\;{{m}}}}({{x}} + 4) \Rightarrow \;{{x}} + {{my}} - 3\;{{m}} + 4\; = \;0$ ........(2)

समकोण त्रिभुज की भुजा BC एवं ${{x}}$ - अक्ष एवं AC ${{y}}$ - अक्ष के समांतर है 

BC का समीकरण होगा ${{y - 1 }}\;{{ = }}\;{{0}}\; \Rightarrow \;{{y}}\;{{ = }}\;{{1}}$

AC का समीकरण होगा ${{x}}\;{{ = }}\;{{1}}$

18. किसी बिन्दु के लिए रेखा को दर्पण मानते हुए बिन्दु ${{(3,8)}}$ का रेखा ${{x + 3y  =  7 }}$ मे प्रतिबिंब ज्ञात कीजिए। 

उत्तर: दिया गया है, ${{x + 3y  =  7 }}$ ........(1)

${{y  = }}\;{{ - }}\dfrac{{{1}}}{{{3}}}{{x + }}\dfrac{{{7}}}{{{3}}}$

बिन्दु P ${{(3,8)}}$ और उसके प्रतिबिंब Q से होकर जाने वाली रेखा होगा और PQ रेखा ${{x + 3y  =  7 }}$ के लम्ब होगी  

अतः PQ की ढाल = ${{3}}$

PQ का समीकरण होगा, 

${{y - 8}}\;{{ = }}\;{{3(x - 3)}} \Rightarrow \;{{3x - y + 5}}\; = \;0$ ........(2)

अतः समीकरण (1) और (2) को हल करने पर हमे मिलेगा ${{x}}\;{{ = }}\;{{1,}}\;{{y}}\;{{ = }}\;{{2}}$

रेखा (1) और (2), ${{(1,2)}}$ पर प्रतिच्छेद करेंगे 

O ${{(1,2)}}$ , PQ का मध्य बिन्दु है। मान लेते है कि Q के निर्देशांक ${{(a ,b)}}$ होंगे 

$\therefore \;\dfrac{{{{a}} + 3}}{2}\; = \;1,\;\dfrac{{{{b}} + 8}}{2}\; = \;2 \Rightarrow \;{{a}}\; = \; - 1,\;\;{{b}}\; = \; - 4$

P के प्रतिबिंब Q के निर्देशांक होंगे $( - 1, - 4)$

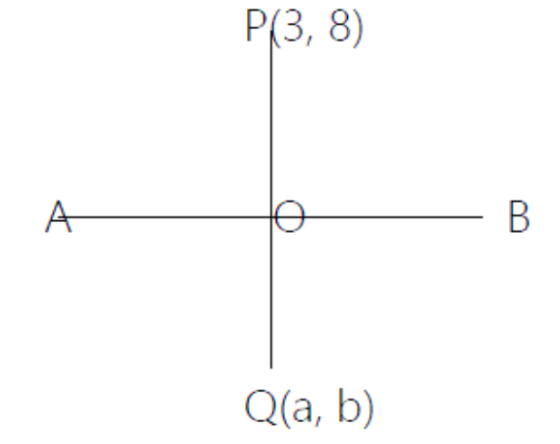
19. यदि रेखाए ${{y  =  3x  + 1, 2y  =  x + 3 }}$ रेखा ${{y  =  mx  + 4}}$ पर समान रूप से आनत हो तो ${{m}}$ का मान ज्ञात कीजिए। 

उत्तर: दिया गया है, 

${{y  =  3x  + 1}}$ ..........(1)

${{2y  =  x + 3 }}$…….(2)

${{y  =  mx  + 4}}$ ..........(3)

मान लेते है कि रेखा (1) और रेखा (2) रेखा (3) के साथ $\theta $ कोण बना रही है

${{y}}\;{{ = }}\;{{3x + 1}} \Rightarrow \;{{{m}}_{{1}}}\;{{ = }}\;{{3}}$

${{y}}\;{{ = }}\;\dfrac{{{1}}}{{{2}}}{{x + }}\dfrac{{{3}}}{{{2}}} \Rightarrow {{{m}}_{{2}}}\;{{ = }}\;\dfrac{{{1}}}{{{2}}}$

$\therefore \;{{tan\theta }}\;{{ = }}\;{{ \pm }}\dfrac{{{{m - 3}}}}{{{{1 + 3m}}}}{{tan\theta }}\;{{ = }}\;\dfrac{{{{2m - 1}}}}{{{{2 + m}}}}$

(i) $\dfrac{{{{m}} - 3}}{{1 + 3\;{{m}}}}\; = \;\dfrac{{2\;{{m}} - 1}}{{2 + {{m}}}} \Rightarrow \;({{m}} - 3)(2 + {{m}})\; = \;(2\;{{m}} - 1)(1 + 3\;{{m}})$

$\Rightarrow \;6\;{{{m}}^2} - {{m}} - 1\; = \;{{{m}}^2} - {{m}} - 1 \Rightarrow \;{{{m}}^2}\; = \; - 1$

चूंकि यह वास्तविक संख्या नहीं है आठ ${{{m}}^2}\; = \; - 1$ मान्य नहीं है।

(ii) $\dfrac{{{{m}} - 3}}{{1 + 3\;{{m}}}}\; = \; - \dfrac{{2\;{{m}} - 1}}{{2 + {{m}}}} \Rightarrow \;({{m}} - 3)(2 + {{m}})\; = \;( - 2\;{{m + }}1)(1 + 3\;{{m}})$

$\Rightarrow \;7{{{m}}^2} - 2\;{{m}} - 7\; = \;0$

$\therefore \;{{m}} = \;\dfrac{{2 \pm \sqrt {4 + 4 \times 49} }}{{14}} \Rightarrow {{m}}\; = \;\dfrac{{1 \pm 5\sqrt 2 }}{7}$

20. यदि एक कहर बिन्दु P ${{(x,y)}}$ की रेखाओ ${{x + y}}\;{{ = }}\;5{{,}}\;3{{x - 2y + 7}}\;{{ = }}\;{{0}}$ से लांबिक दूरियों का योग सदैव दस रहे तो दर्शाइए कि अनिवार्य रूप से एक पर गमन करता है। 

उत्तर: P ${{(x,y)}}$ की रेखा ${{x + y}}\;{{ = }}\;5$ से लांबिक दूरी = $\dfrac{{{{x + y - 5}}}}{{\sqrt {{2}} }}$ 

और P ${{(x,y)}}$ की रेखा $3{{x - 2y + 7}}\;{{ = }}\;{{0}}$ से लांबिक दूरी = $\dfrac{{{{3x - 2y - 7}}}}{{\sqrt {13} }}$

दिया गया है कि लांबिक दूरियों का योग = $10$

$\Rightarrow \;\dfrac{{{{x + y - 5}}}}{{\sqrt {{2}} }}{{ + }}\dfrac{{{{3x - 2y - 7}}}}{{\sqrt {{{13}}} }}\;{{ = }}\;{{10}}$

$\Rightarrow \;({{x}} + {{y}} - 5)\sqrt {13}  + (3{{x}} - 2{{y}} - 7)\sqrt 2 \; = \;10\sqrt {26}$

$\Rightarrow \;(\sqrt {13}  + 3\sqrt 2 ){{x}} + (\sqrt {13}  - 2\sqrt 2 ){{y}} - 5\sqrt {13}  + 7\sqrt 2  - 10\sqrt {26} \; = \;0$

यह एक सरल रेखा का समीकरण है। आठ P अनिवार्य रूप से एक रेखा पर गमन करता है।

21 . समांतर रेखाओ ${{9x - 6y - 7}}\;{{ = }}\;{{0,}}\;3{{x + 2y + 6}}\;{{ = }}\;{{0}}$ से संदूरस्त रेखा का समीकरण ज्ञात कीजिए। 

उत्तर: दिया गया है, 

${{9x - 6y - 7}}\;{{ = }}\;{{0}}$ .......(1)

$3{{x + 2y + 6}}\;{{ = }}\;{{0}}$ ..........(2)

मान लेते है P ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ एक बिन्दु है जिसकी रेखा (1) और रेखा (2) से दूरी बराबर है 

P ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ कि रेखा (1) से दूरी, ${{{d}}_1}\; = \;\dfrac{{\left| {9{{{x}}_1} - 6{{{y}}_1} - 7} \right|}}{{\sqrt {{9^2} + {6^2}} }}\; = \;\dfrac{{\left| {9{{{x}}_1} - 6{{{y}}_1} - 7} \right|}}{{\sqrt {117} }}\; = \;\dfrac{{\left| {9{{{x}}_1} - 6{{{y}}_1} - 7} \right|}}{{3\sqrt {13} }}$

P ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ कि रेखा (2) से दूरी, ${{{d}}_2}\; = \;\dfrac{{\left| {3{{{x}}_1} + 2{{{y}}_1} + 6} \right|}}{{\sqrt {{3^2} + {2^2}} }}\; = \;\dfrac{{\left| {3{{{x}}_1} + 2{{{y}}_1} + 6} \right|}}{{\sqrt {13} }}$

P ${{(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{)}}$ कि रेखा (1) और रेखा (2) से दूरी बराबर है

$\dfrac{{\left| {9{{{x}}_1} - 6{{{y}}_1} - 7} \right|}}{{3\sqrt {13} }}\; = \;\dfrac{{\left| {3{{{x}}_1} + 2{{{y}}_1} + 6} \right|}}{{\sqrt {13} }}$

$9{{{x}}_1} - 6{{{y}}_1} - 7\; = \; \pm 3\left( {3{{{x}}_1} + 2{{{y}}_1} + 6} \right)$

$9{{{x}}_1} - 6{{{y}}_1} - 7\; = \;3\left( {3{{{x}}_1} + 2{{{y}}_1} + 6} \right)$

${{18}}{{{x}}_1}{{ + 12}}{{{y}}_1} + 11\; = \;0$

आठ रेखाओ ${{9x - 6y - 7}}\;{{ = }}\;{{0,}}\;3{{x + 2y + 6}}\;{{ = }}\;{{0}}$ समदूरस्थ रेखा का समीकरण होगा ${{18x + 12y}} + 11\; = \;0$

22. बिन्दु $(1,2)$ से होकर जाने वाली एक प्रकाश किरण ${{x}}$ - अक्ष के बिन्दु A से परिवर्तित होती है और परिवर्तित किरण बिन्दु ${{(5,3)}}$ से होकर जाती है। A के निर्देशांक ज्ञात कीजिए। 

उत्तर: मान लेते है कि रेखा XX’, ${{x}}$ - अक्ष के अनुदिश है। आठ XX’ के पर के A निर्देशांक ${{(k,0)}}$ है। 

आपतित कोण = परिवर्तित कोण

$\therefore \;\tan \theta \; = \;\tan \left( {{{180}^\circ } - \theta } \right)$

$\angle {{QAX}}\; = \;\theta$

$\therefore \;\angle {{OAP}}\; = \;{180^\circ } - \left[ {\theta  + 2\left( {{{90}^\circ } - \theta } \right)} \right]\;$

$= \;{180^\circ } - \theta  - {180^\circ } + 2\theta \; = \;\theta$

$\therefore \;\angle {{PAX}}\; = \;{180^\circ } - \theta$

AX कि ढाल = ${{tan\theta }}\;{{ = }}\;\dfrac{{{{0 - 3}}}}{{{{k - 5}}}}\;{{ = }}\;\dfrac{{{{ - 3}}}}{{{{k - 5}}}}$

AX’ ई ढाल = ${{tan(180^\circ  - \theta )}}\;{{ = }}\;\dfrac{{{{0 - 2}}}}{{{{k - 1}}}}\;{{ = }}\;\dfrac{{{{ - 2}}}}{{{{k - 1}}}}$

${{tan(180^\circ  - \theta )}}\;{{ = }}\;{{ - tan\theta }}$

$\dfrac{{{{ - 3}}}}{{{{k - 5}}}}\;{{ = }}\;\dfrac{{{{ - 2}}}}{{{{k - 1}}}} \Rightarrow \;3({{k}} - 1)\; = \; - 2({{k}} - 5) \Rightarrow \;5{{k}}\; = \;13 \Rightarrow \;{{k}}\; = \;\dfrac{{13}}{5}$

A निर्देशांक $(\dfrac{{13}}{5},0)$ है।

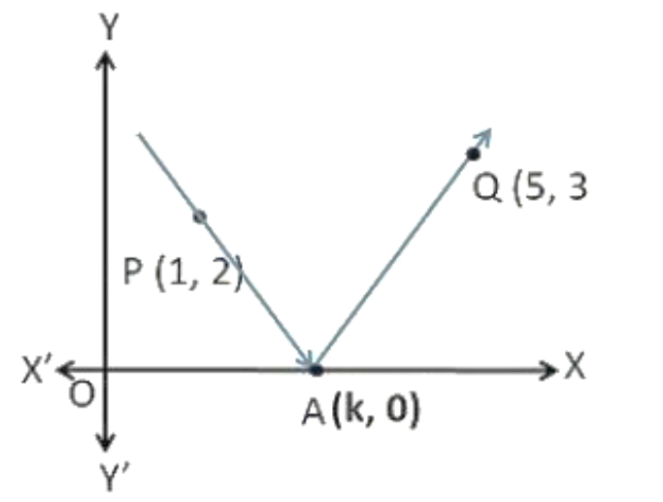
23. दिखाइए कि ${{(}}\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} {{,0),}}\;{{( - }}\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} {{,0)}}$ बिन्दुओ से रेखा $\dfrac{{{x}}}{{{a}}}{{cos\theta  + }}\dfrac{{{y}}}{{{b}}}{{sin\theta }}\;{{ = }}\;{{1}}$ पर खींचे गए लंबों की लम्बाइया का गुणनफल ${{{b}}^2}$ होगा। 

उत्तर: दिया गया है $\dfrac{{{x}}}{{{a}}}{{cos\theta  + }}\dfrac{{{y}}}{{{b}}}{{sin\theta }}\;{{ = }}\;{{1}}$

${{(}}\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} {{,0)}}$ से खींचे गए लंब कि लंबाई ${{{P}}_{{1}}}\;{{ = }}\;\dfrac{{\dfrac{{\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} }}{{{a}}}{{cos\theta  + 0 - 1}}}}{{\sqrt {\dfrac{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta }}}}{{{{{b}}^{{2}}}}}} }}$

${{( - }}\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} {{,0)}}$ से खींचे गए लंब कि लंबाई ${{{P}}_2}\;{{ = }}\;\dfrac{{\dfrac{{\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} }}{{{a}}}{{cos\theta  + 0 - 1}}}}{{\sqrt {\dfrac{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta }}}}{{{{{b}}^{{2}}}}}} }}$

${{{P}}_{{1}}}{{ \times }}{{{P}}_{{2}}}\;{{ = }}\;\dfrac{{\dfrac{{\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} }}{{{a}}}{{cos\theta  - 1}}}}{{\sqrt {\dfrac{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta }}}}{{{{{b}}^{{2}}}}}} }}{{ \times }}\dfrac{{{{ - }}\dfrac{{\sqrt {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} }}{{{a}}}{{cos\theta  - 1}}}}{{\sqrt {\dfrac{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta }}}}{{{{{b}}^{{2}}}}}} }}\;{{ = }}\;\dfrac{{{{1 - }}\dfrac{{{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}}}{{{{{a}}^{{2}}}}}{{co}}{{{s}}^{{2}}}{{\theta }}}}{{\dfrac{{{{co}}{{{s}}^{{2}}}{{\theta }}}}{{{{{a}}^{{2}}}}}{{ + }}\dfrac{{{{si}}{{{n}}^{{2}}}{{\theta }}}}{{{{{b}}^{{2}}}}}}}\;{{ = }}\;\dfrac{{{{{b}}^{{2}}}\left[ {{{ - }}\left( {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} \right){{co}}{{{s}}^{{2}}}{{\theta  + }}{{{a}}^{{2}}}} \right]}}{{{{{b}}^{{2}}}{{co}}{{{s}}^{{2}}}{{\theta  + }}{{{a}}^{{2}}}{{si}}{{{n}}^{{2}}}{{\theta }}}}$

${{ = }}\;\dfrac{{{{ - }}{{{b}}^{{2}}}\left[ {\left( {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} \right){{co}}{{{s}}^{{2}}}{{\theta  - }}{{{a}}^{{2}}}} \right]}}{{{{{b}}^{{2}}}{{co}}{{{s}}^{{2}}}{{\theta  + }}{{{a}}^{{2}}}\left( {{{1 - co}}{{{s}}^{{2}}}{{\theta }}} \right)}}\;{{ = }}\;\dfrac{{{{ - }}{{{b}}^{{2}}}\left[ {\left( {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} \right){{co}}{{{s}}^{{2}}}{{\theta  - }}{{{a}}^{{2}}}} \right]}}{{{{ - }}\left[ {\left( {{{{a}}^{{2}}}{{ - }}{{{b}}^{{2}}}} \right){{co}}{{{s}}^{{2}}}{{\theta  - }}{{{a}}^{{2}}}} \right]}}\;{{ = }}\;{{{b}}^{{2}}}$

24. एक व्यक्ति समीकरण ${{2x - 3y + 4}}\;{{ = }}\;{{0,}}\;3{{x + 4y - 5}}\;{{ = }}\;{{0}}$ से निरूपित सरल रेखीय पथों के संधि बिन्दु पे खड़ा है और समीकरण ${{6x - 7y + 8}}\;{{ = }}\;{{0}}$ से निरूपित पथ पर न्यूटम समय मे पहुचना चाहता है। उसके द्वारा अनुसरित पथ का समीकरण ज्ञात कीजिए। 

उत्तर: दिया गया है, 

${{2x - 3y + 4}}\;{{ = }}\;{{0}}$ ........(1)

$3{{x + 4y - 5}}\;{{ = }}\;{{0}}$ ........(2)

${{6x - 7y + 8}}\;{{ = }}\;{{0}}$ ........(3)

समीकरण (1) और (2) को हल करने पर हमे मिलेगा ${{x}}\;{{ = }}\;{{ - }}\dfrac{{{1}}}{{{{17}}}}{{,}}\;{{y}}\;{{ = }}\;\dfrac{{{{22}}}}{{{{17}}}}$

आठ व्यक्ति ${{( - }}\dfrac{{{1}}}{{{{17}}}}{{,}}\dfrac{{{{22}}}}{{{{17}}}})$ पर खड़ा है। 

${{6x - 7y + 8}}\;{{ = }}\;{{0}}$ से निरूपित पथ तक फूचने मे उसे न्यूटम समय तब लगेगा जब वह कम से कम दूरी तय करेगा। अतः उसे ${{6x - 7y + 8}}\;{{ = }}\;{{0}}$ से लम्बवत दिशा मे चलना होगा। 

${{6x - 7y + 8}}\;{{ = }}\;{{0}}$ से लम्बवत रेखा कि ढाल = ${{ - }}\dfrac{7}{6}$

${{( - }}\dfrac{{{1}}}{{{{17}}}}{{,}}\dfrac{{{{22}}}}{{{{17}}}})$ से जाने वाली रेखा जिसकी ढाल ${{ - }}\dfrac{7}{6}$ है का समीकरण होगा

${{y - }}\dfrac{{{{22}}}}{{{{17}}}}\;{{ = }}\;{{ - }}\dfrac{{{7}}}{{{6}}}\left( {{{x + }}\dfrac{{{1}}}{{{{17}}}}} \right)$

$\therefore \;{{6(17y - 22)}}\;{{ = }}\;{{ - 7(17x + 1)}}$

$\Rightarrow \;{{102y - 132}}\;{{ = }}\;{{ - 119x - 7}}$

$\Rightarrow \;{{109x + 102y}}\;{{ = }}\;{{125}}$

NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 11 Maths Chapter 10 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 11 Maths Chapter 10 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 11 Maths Chapter 10 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 11 Maths Straight Lines solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 11 Maths Straight Lines in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 11 can download these solutions at any time as per their convenience for self-study purpose.

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 11 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.