NCERT Solutions for Class 12 Maths In Hindi Chapter 8 Application of Integrals

प्रश्नावली 8.1

1. वक्र \[{{\mathbf{y}}^{\mathbf{2}}} = {\mathbf{x}}\] रेखाओ \[{\mathbf{x}} = {\mathbf{1}},{\text{ }}{\mathbf{x}} = {\mathbf{4}}\] एवं \[{\mathbf{x}}\] अक्ष से घिरे का प्रथम पाद में क्षेत्रफल ज्ञात कीजिए।

उत्तर : अभीष्ट क्षेत्रफल

$ = \int_{x = 1}^4 y dx = \int_1^4 {\sqrt x } dx$

$= \left[ {\frac{{{x^3}/2}}{{\frac{3}{2}}}} \right]_1^4$

$= \frac{2}{3}\left[ {{{(4)}^{3/2}} - {{(1)}^{3/2}}} \right]$

$= \frac{2}{3}[8 - 1]$

$= \frac{{14}}{3}$ 

2. प्रथम चतुथाश में वक्र \[{{\mathbf{y}}^{\mathbf{2}}} = {\mathbf{9x}},{\text{ }}{\mathbf{x}} = {\mathbf{2}},{\text{ }}{\mathbf{x}} = {\mathbf{4}}\] एवं \[{\mathbf{x}}\] अक्ष से घिरे का क्षेत्रफल ज्ञात कीजिए।

उत्तर : अभीष्ट क्षेत्रफल

$\int_2^4 y dx = \int_2^4 {\sqrt {9x} } dx \ldots  \ldots  \ldots  \ldots \left[ {{y^2} = 9x} \right]$

$= 3\int_2^4 {\sqrt x } dx = 3\left[ {\frac{{{x^{3/2}}}}{{\frac{3}{2}}}} \right]_3^4$ 

$= 2\left[ {{4^{3/2}} - {2^{3/2}}} \right]$

$= 2[\sqrt {64}  - \sqrt 8 ]$

$= 2[8 - 2\sqrt 2 ]$

$= (16 - 4\sqrt 2 )$ 

3. प्रथम चतुथाश में \[{{\mathbf{x}}^{\mathbf{2}}} = {\mathbf{4y}},{\text{ }}{\mathbf{y}} = {\mathbf{2}},{\text{ }}{\mathbf{y}} = {\mathbf{4}}\] वक्र एवं \[{\mathbf{y}}\] अक्ष से घिरे का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दिया हुआ वक्र ${x^2} = 4y,y$ अक्ष के प्रति सममित है तथा हमें प्रथम चतुथाश के क्षेत्रफल ज्ञात करना
∴ अभीष्ट क्षेत्रफल = क्षेत्रफल $ABCDA$

$= \int_2^4 x dy = \int_2^4 2 \sqrt y dy \ldots  \ldots  \ldots [\because x = 2\sqrt y ]$

$= 2\left[ {\frac{{{y^{3/2}}}}{{\frac{3}{2}}}} \right]_3^4$

$= \frac{4}{3}\left[ {{{(4)}^{3/2}} - {{(2)}^{3/2}}} \right]$

$= \frac{4}{3}[\sqrt {64}  - \sqrt 8 ]$

$= \frac{4}{3}[8 - 2\sqrt 2 ]$

$= \frac{{32 - 8\sqrt 2 }}{3}$ 

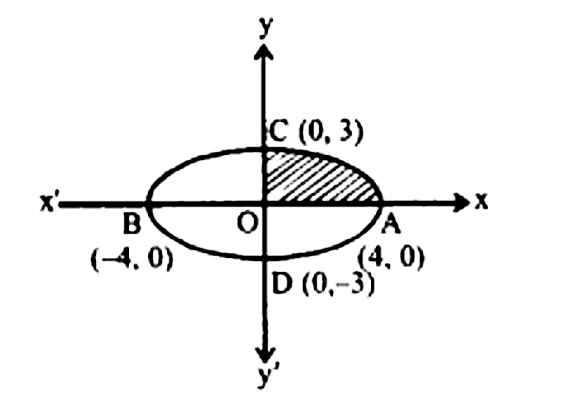
4. दीघ्रशवृत्त् $\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1$ से घिरे का क्षेत्रफल ज्ञात कीजिए ।

उत्तर : दिया गया दीघ्रशवृत्त् का समीकरण $ = \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1$
दिया गए दीर्घवृत्त दोनों अक्ष के बारे में सममित है, इसमें समरूप $x$ और $y$ समाहित हैं

\[= \frac{{{y^2}}}{9} = 1 - \frac{{{x^2}}}{{16}}\]

$= y =  \pm \frac{3}{4}\left( {\sqrt {16 - {x^2}} } \right)$

दीर्घवृत्त द्वारा घिरा क्षेत्रफल $= 4$ (क्षेत्र का क्षेत्रफल) $ = 4$ (क्षेत्रफल $OAC$)
पहले चतुर्भुज में दीर्घवृत्त
माना $x = 4{\text{sin}}\theta ;dx = 4{\text{cos}}\theta d\theta $

अत: $x = 0,\theta  = 0$ ; जब $x = 4,\theta  = \frac{\pi }{2}$

अपेक्षित क्षेत्र 

$= 48\int_0^{\frac{\pi }{2}} {{{\cos }^2}} \theta d\theta $

$= 24\int_0^{\frac{\pi }{2}} {(1 + \cos 2\theta )} d\theta $

$= 24\left[ {\theta  + \frac{{\sin 2\theta }}{2}} \right]_0^{\frac{\pi }{2}}$

$= 12\pi$

5. दीघ्रशवृत्त् $\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1$ से घिरे का क्षेत्रफल ज्ञात कीजिए ।

उत्तर : दिया गया दीघ्रशवृत्त् का समीकरण $ = \frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1$

$\because 9 > 4$

$\frac{{{y^2}}}{9} = 1 - \frac{{{x^2}}}{4} = \frac{{4 - {x^2}}}{4}$

$\Rightarrow \frac{y}{3} =  \pm \sqrt {\frac{{4 - {x^2}}}{4}} $

$\Rightarrow  \pm \frac{{\sqrt {4 - {x^2}} }}{4}$ 

$y =  \pm \frac{3}{2}\sqrt {4 - {x^2}}$

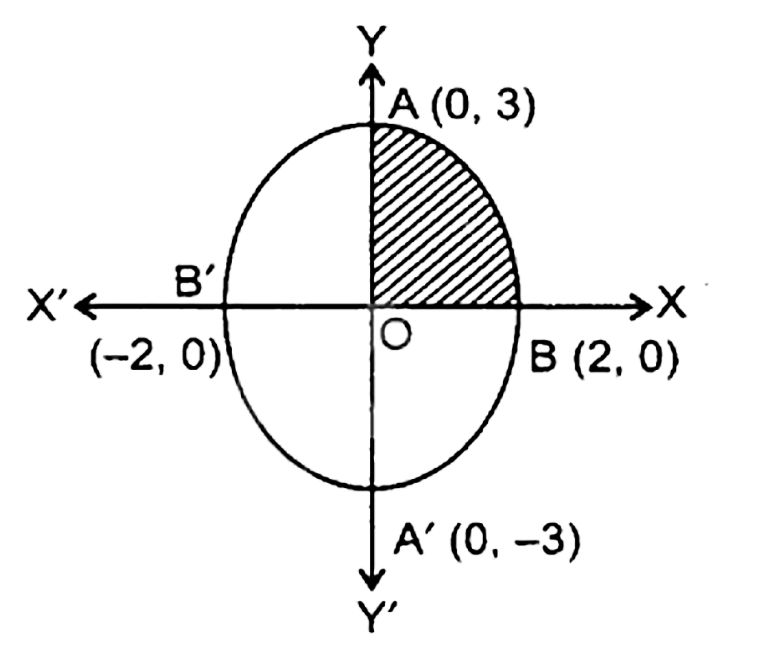
दिया गए दीर्घवृत्त दोनों अक्ष के बारे में सममित है, इसमें समरूप $x$ और $y$ समाहित हैं

दीर्घवृत्त द्वारा घिरा क्षेत्रफल $ = 4$ ( क्षेत्र काक्षेत्रफल) \[ = {\text{ }}4\](क्षेत्रफल $AOC$)

$= 4\int_0^2 {\frac{3}{2}} \sqrt {4 - {x^2}} dx$

$= 6\int_0^2 {\sqrt {4 - {x^2}} } dx$

$= 6\left[ {\frac{{x\sqrt {4 - {x^2}} }}{2} + \frac{4}{2}{{\sin }^{ - 1}}\frac{x}{2}} \right]_0^2$

$= 6\left[ {\left( {0 + 2{{\sin }^{ - 1}}(1)} \right) - \left( {0 + {{\sin }^{ - 1}}(0)} \right)} \right]$

$= 12{\sin ^{ - 1}}1$

$= 12 \times \frac{\pi }{2}$

$= 6\pi {\text{ }}$ 

6. प्रथम चतुथाश में व्रत ${x^2} + {y^2} = 4$ रेखा $x = 3\sqrt 3 y$ एवं $x$ अक्षा से द्वारा घिरे में क्षेत्रफल ज्ञात कीजिए।

उत्तर : (i) दिया गया व्रत का समीकरण ${x^2} + {y^2} = 4$ है जिसका केंद्र $\left( {0,0} \right)$ और त्रिज्या \[2\] के सामान

$y = \sqrt {4 - {x^2}} $

${x^2} + {y^2} = 4 \ldots  \ldots  \ldots (1)$

$x = \sqrt {3y}  \ldots  \ldots  \ldots  \ldots (2)$ 

समी (2) से $x$ का मान समीकरण (1) में रखने पर

${(\sqrt 3 y)^2} + {y^2} = 4$

$\Rightarrow 4{y^2} = 4$

$\Rightarrow y =  \pm 1$

$x = \sqrt 3 $ 

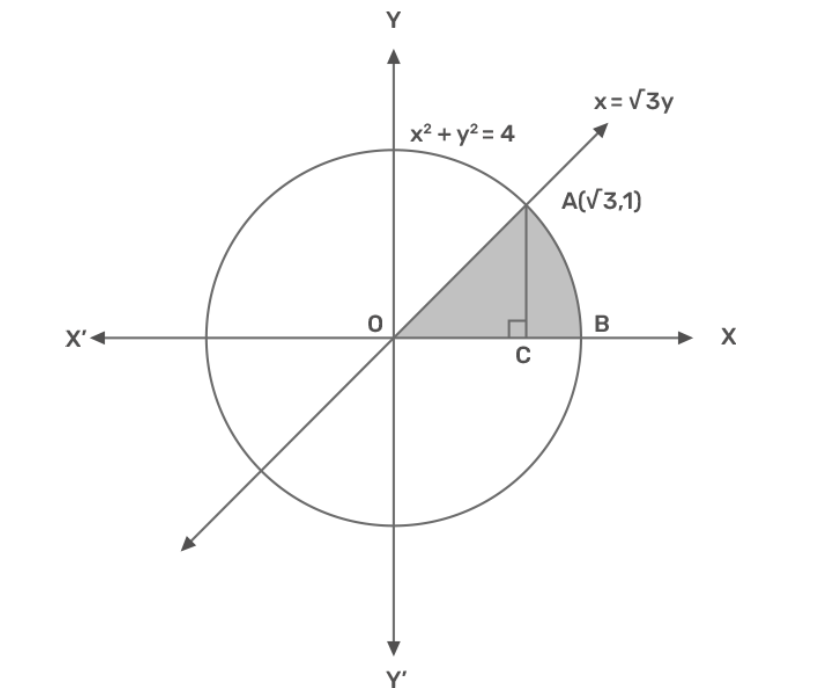
(ii) सरल रेखा का समीकरण $x = 3\sqrt 3 y$ है जो बिंदु $\left( {0,0} \right),\left( {\sqrt 3 ,1} \right)$ से हो कर जाता

$y = \frac{x}{{\sqrt 3 }}$

$\therefore $अभीष्ट क्षेत्रफल\[ = \] क्षेत्रफल \[0{\text{BL}}\]\[ + \] क्षेत्रफल\[LBA\]

$= \frac{1}{{\sqrt 3 }}\int_0^{\sqrt 3 } x dx + \int_{\sqrt 3 }^2 {\sqrt {4 - {x^2}} } dx$

$= \frac{1}{{\sqrt 3 }}\left[ {\frac{{{x^2}}}{2}} \right]_0^{\sqrt 3 } + \left[ {\frac{{x\sqrt {4 - {x^2}} }}{2} + \frac{4}{2}{{\sin }^{ - 1}}\left( {\frac{x}{2}} \right)} \right]_{\sqrt 3 }^2$

$= \frac{1}{{2\sqrt 3 }}(3 - 0) + \left[ {\left( {0 - \frac{{\sqrt 3 }}{2}} \right) + 2\left( {{{\sin }^{ - 1}}1 - {{\sin }^{ - 1}}\left( {\frac{{\sqrt 3 }}{2}} \right)} \right)} \right]$

$= \frac{{\sqrt 3 }}{2} - \frac{{\sqrt 3 }}{2} + 2\left( {\frac{\pi }{2} - \frac{\pi }{3}} \right)$

$= 2\left( {\frac{{3\pi  - 2\pi }}{6}} \right)$

$= \frac{\pi }{3}{\text{ }}$ 

7. छेदक रेखा $x = \frac{a}{{\sqrt 2 }}$ द्वारा व्रत ${x^2} + {y^2} = {a^2}$ के छोटे भाग का क्षेत्रफल ज्ञात कीजिए|

उत्तर : अभीष्ट क्षेत्रफल $ = 2$ (क्षेत्रफल $MAPM)$

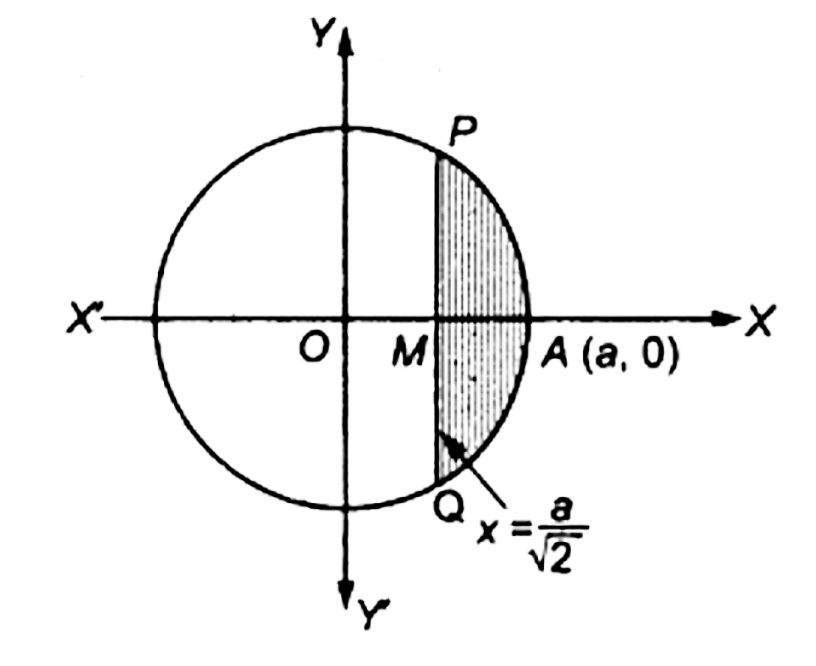
क्योंकि व्रत $x$ अक्ष कि प्रति सममित है

$= 2\int_{a/\sqrt 2 }^a y dx = 2\int_{a/\sqrt 2 }^a {\sqrt {{a^2} - {x^2}} } dx \ldots  \ldots  \ldots {x^2} + \left. {{y^2} = {a^2}} \right]$

$= 2\left| {\frac{x}{2}\sqrt {{a^2} - {x^2}}  + \frac{{{a^2}}}{2}{{\sin }^{ - 1}}\frac{x}{a}} \right|_{\frac{a}{{\sqrt 2 }}}^a$

$= 0 + {a^2}{\sin ^{ - 1}}1 - \frac{a}{{\sqrt 2 }}\sqrt {{a^2} - \frac{{{a^2}}}{2}}  - {a^2}{\sin ^{ - 1}}\frac{1}{{\sqrt 2 }}$

$= {a^2}\frac{\pi }{2} - \frac{a }{{\sqrt 2 }}\frac{a }{{\sqrt 2 }} - {a^2}\frac{\pi }{4}$

$= \frac{{{a^2}\pi }}{2} - \frac{{{a^2}}}{2} - \frac{{\pi {a^2}}}{4}$

$= \frac{{\pi {a^2}}}{4} - \frac{{{a^2}}}{2}$

$= \frac{{{a^2}}}{2}\left( {\frac{\pi }{2} - 1} \right)$

8. यदि वक्र $x = {y^2}$ एवं रेखा \[\;x = 4\] से घिर्रे का क्षेत्रफल रेखा $x = a$ द्वारा दो बराबर भागो में विभाजित होता है तो $a$ मान ज्ञात कीजिए ।

उत्तर :  दिया गया व्रत है, 

$x = {y^2} \ldots  \ldots  \ldots {\text{ (1) }}$

$x = 4 \ldots  \ldots (2)$ 

एक रेखा एक परवलय जिसको शीर्ष है तथा एक रेखा है जो कि अक्ष कि सामन्तर है तथा इस से इकाई दूरी पर है । माना रेखा को दो बराबर भागो में विभाजित करती है । इस लिए कुल क्षेत्रफल

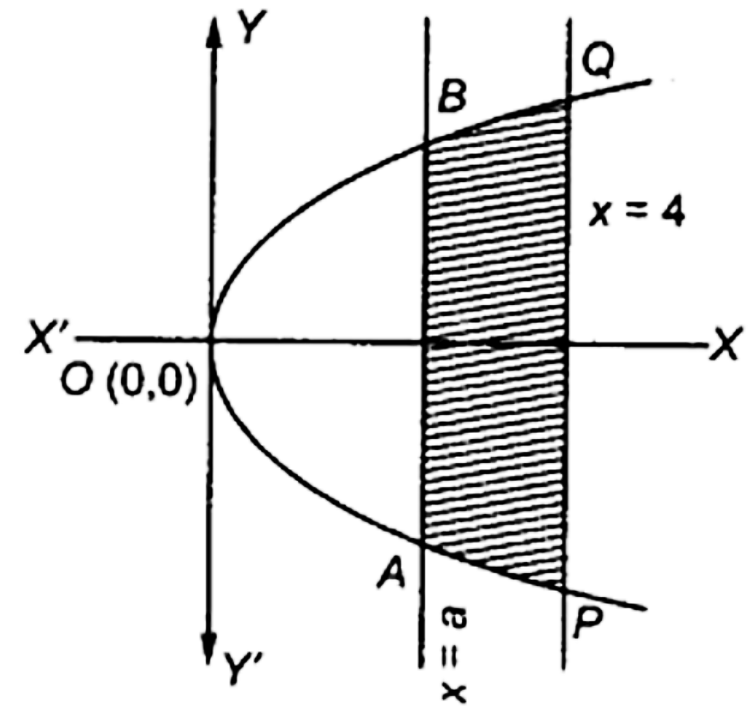
OPQP = 2OABO

$2\int_0^4 {\sqrt x } dx = 2.2\int_0^a {\sqrt x } dx \ldots  \ldots  \ldots  \ldots  \ldots  \ldots ..\left[ {\because {y^2} = x \Rightarrow y = } \right.\sqrt x ],$

$x = a$

$\Rightarrow \left[ {\frac{{{x^3}/2}}{{\frac{3}{2}}}} \right]_0^4 = 2\left[ {\frac{{{x^{3/2}}}}{{\frac{3}{2}}}} \right]_0^a$

$\Rightarrow \frac{2}{3}{(4)^{3/2}} = \frac{4}{3}{(a)^{3/2}}$

$\Rightarrow \frac{8}{2} = {(a)^{3/2}}$

$\Rightarrow 4 = {(a)^{\frac{3}{2}}}$

$\Rightarrow a = {(4)^{2/3}}$

 
9. परवलये $y = {x^2}$ एवं \[{\text{y = |x|}}\] से घिरे का क्षेत्रफल ज्ञात कीजिए ।

उत्तर : दिया गया परवलये,

$y = {x^2}y$ अक्ष क़े प्रति सममित है। 

परवलय  $y = {x^2};y = x$ क़े प्रतिच्छेद बिंदु क़े लिए। 

$y = {x^2}$ में $y = x$ रखने पर, 

$x = {x^2}$

$\Rightarrow x(x - 1) = 0$

$\Rightarrow x = 0,x = 1$ 

 क्योंकि y = |x|

therefore y = x

अत: अभीष्ट प्रतिच्छेद बिंदु \[{\text{( - 1,1),(0,0),(1,1)}}\,\]

इसलिए अभीष्ट क्षेत्रफल $= 2[$क्षेत्रफल $\vartriangle {\text{APO  -  }}$ क्षेत्रफल $\vartriangle {\text{OAP}}]$

$= 2\left[ {\int_0^1 x dy - \frac{1}{2}(1)(1)} \right]$

$= 2\left[ {\int_0^1 {\sqrt y } dy - \frac{1}{2}} \right]$ 

$= 2\left[ {\frac{{{y^{3/2}}}}{{\frac{3}{2}}}} \right]_0^1 - 1$

$= \frac{4}{3}(1 - 0) - 1$

$= \frac{1}{3}$ 

10. वक्र ${x^2} = 4y$ एवं रेखा $x = 4y - 2$ से घ्रिरे का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दिया गया वक्र, ${x^2} = 4y...(1)$

तथा दी गई रेखा $x = 4y - 2...(2)$

(1) और (2) को हल करने पर

${(4y - 2)^2} = 4y$

$\Rightarrow 16{y^2} - 16y + 4 - 4y = 0$

$\Rightarrow 16{y^2} - 20y + 4 = 0$

$\Rightarrow 4{y^2} - 5y + 1 = 0$

$\Rightarrow (y - 1)(4y - 1) = 0$

$\Rightarrow y = 1,\frac{1}{4}$ 

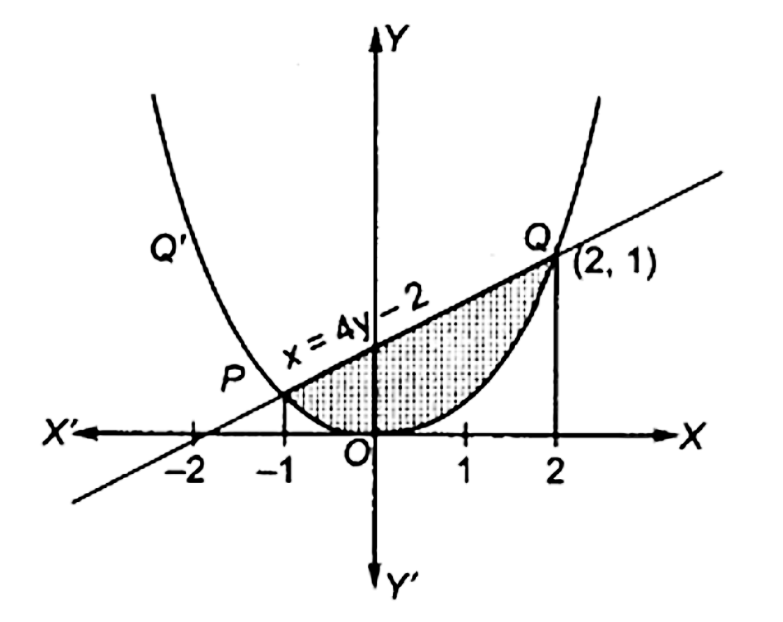
$y = 1,x = 4 - 2 = 2$

$y = \frac{1}{4},x = 1 - 2 = 2$ 

वक्र और रेखा क़े प्रतिच्छेद बिंदु  $P\left( { - 1,\frac{1}{4}} \right)$ और \[{\text{Q(2,1)}}\] है इसलिए अभीष्ट क्षेत्रफल

$ = \int_{ - 1}^2 {\left( {\frac{{x + 2}}{4} - \frac{1}{4}{x^2}} \right)} dx = \frac{1}{4}\int_{ - 1}^2 {\left( {x + 2 - {x^2}} \right)} dx$

$= \frac{1}{4}\left[ {\frac{{{x^2}}}{2} + 2x - \frac{{{x^3}}}{3}} \right]_{ - 1}^2$

$= \frac{1}{4}\left[ {\left( {2 + 4 - \frac{8}{3}} \right) - \left( {\frac{1}{2} - 2 + \frac{1}{3}} \right)} \right]$

$= \frac{1}{4}\left[ {\left( {6 - \frac{8}{3}} \right) + 2 + \frac{5}{6}} \right)$

$= \frac{1}{4}\left[ {\frac{{10}}{3} + 2 - \frac{5}{6}} \right]$ 

$= \frac{1}{4}\left[ {\frac{{20 + 12 - 5}}{6}} \right]$

$= \frac{1}{4}\left( {\frac{{27}}{6}} \right)$

$= \frac{9}{8}$ 

11. वक्र ${y^2} = 4x$ एवं रेखा $x = 3$ से घिरे का क्षेत्रफल ज्ञात कीजिए|

उत्तर : दिया गया वक्र ${y^2} = 4x$ एक परवलय समीकरण है। जिसको शीर्ष है $(0,0)$ और $OX$ इसका अक्ष है जिसके सापेक्ष परवलय तथा रेखा का समीकरण $x = 3$ है|

${y^2} = 4x....(1)$

$x = 3$

${y^2} = 4 \times 3$

${y^2} = 12$

$\Rightarrow y = \sqrt {12}$ 

अभीष्ट क्षेत्रफल = क्षेत्र \[O{\text{ }}P{\text{ }}Q\]क्षेत्रफल 

=2 $ \times OLQ$ क्षेत्रफल

केवल प्रथम चतुथाश में छायाकिंत क्षेत्र

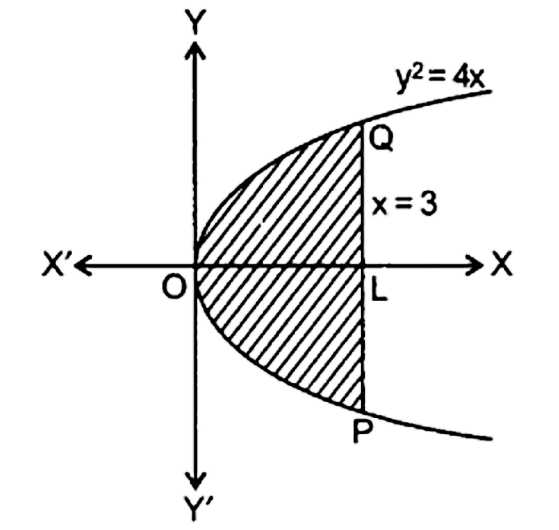
$= 2\int_0^3 y dx = \int_0^3 {\sqrt {4x} } dx$

$= 4\int_0^3 {\sqrt x } dx = 4\left[ {\frac{{{x^{3/2}}}}{{3/2}}} \right]_0^3$

$= 4 \times \frac{2}{3}\left( {{3^3}/2 - 0} \right)$

$= \frac{8}{3} \times 3\sqrt 3$

$= 8\sqrt 3$ 

अभीष्ट क्षेत्रफल $3\sqrt 3$ वर्ग इकाई।

12. प्रथम चतुथाश में वक्र ${x^2} + {y^2} = 4$ एवं रेखाओ $x = 0,x = 2$ से घिरे में क्षेत्रफल है ।

A. $\pi $

B. $\frac{\pi }{2}$

C. $\frac{\pi }{3}$

D. $\frac{\pi }{4}$ 

उत्तर :  दिया गया घेरे का केंद्र में $(0,0)$ और $r = 2$

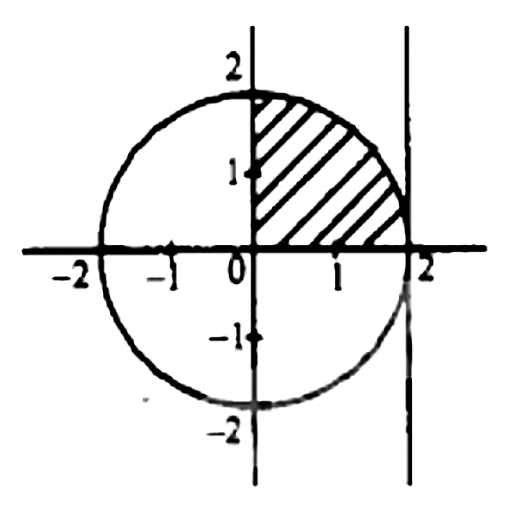
क्षेत्र $= \int_0^2 {\sqrt {4 - {x^2}} } dx$

माना $x = 2\sin \theta  \Rightarrow dx = 2\cos \theta d\theta $ तब $x = 0,\theta  = 0$

$x = 2,\ theta= \frac{\pi }{2}$

क्षेत्र $= \int_0^{\pi /2} 4 {\cos ^2}\theta d\theta {\text{ }}$

\[\left. { = 4\int_0^{\pi /2} {\left( {\frac{{1 + \cos \theta }}{2}} \right)} d\theta  = 2\left( {\theta  + \frac{{\sin \theta }}{2}} \right)} \right]_0^{\pi /2} = \pi \]

अत: \[(A)\] विकल्प सही है।

13. वक्र ${y^2} = 4x,y$ अक्ष एवं रेखा से घ्रि का क्षेत्रफल है।

A. $2$

B. $\frac{9}{4}$

C. $\frac{9}{3}$ 

उत्तर : ${y^2} = 4x$ परवलय है।

क्षेत्र $= \int_0^3 x dy{\text{ }}$

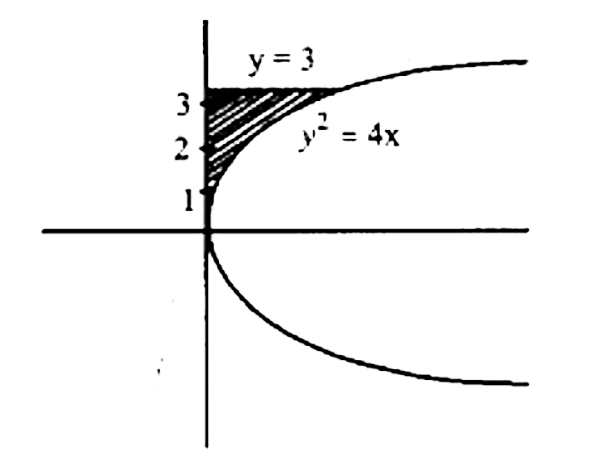
$= \int_0^3 {\frac{{{y^2}}}{4}} dy$

$\left. { = \frac{1}{4} \times \frac{{{y^3}}}{3}} \right]_0^3$

$= \frac{9}{4}$ 

अत: \[(B)\] विकल्प सही है।

प्रश्नावली 8.2

1. परवलय ${x^2} = 4x$ और वृत्त $4{x^2} + 4{y^2} = 9$ के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : वृत्त $= 4{x^2} + 4{y^2} = 9$

परवलय $= {x^2} = 4y$

$\therefore \quad 4(4y) + 4{y^2} = 9$

$4{y^2} + 16y = 9$

$4{y^2} + 16y - 9 = 0$

$y = ( - 16 \pm \sqrt 2 56 + 144)/2 \times 4$

$= ( - 16 \pm \sqrt {400} )/8\quad $

$= ( - 16 \pm 20)/8\quad $

$= 1/2, - 9/2$

$y > 0,y = 1/2$

${x^2} = 4 \times 1/2 = 2$

$x =  \pm \sqrt 2$ 

$= 2\left\{ {\int_0^{\sqrt 2 } V \left( {9 - 4{x^2}} \right)/4dx - \int_0^{\sqrt 2 } {{x^2}} /4dx} \right.$

$= 2\int_0 {\sqrt {{{(3/2)}^2} - {x^2}dx - 2/4\left[ {{x^3}/3} \right]_0^{\sqrt 2 }} } $

$= 2\left[ {x/2\sqrt {{{\left. {{{(3/2)}^2} - {x^2} + {{(3/2)}^2}/2{{\sin }^{ - 1}}(x/3/2)} \right]}_0} - 1/6\left[ {{{(\sqrt 2 )}^3} - 0} \right]} } \right.$

$= {\left[ {x\sqrt 9 /4 - {x^2} + 9/4{{\sin }^{ - 1}}(2x/3)} \right]_0} - 2\sqrt 2 /6$

$= \left[ {\sqrt 2 \sqrt 9 /4 - 2 + 9/4{{\sin }^{ - 1}}(2\sqrt 2 /3)} \right] - \{ 0 - 0\}  - 2\sqrt 2 /6 = \sqrt 2 /2 + 9/4{\sin ^{ - 1}}(2\sqrt 2 /3) - 2\sqrt 2 /6$

$= (\sqrt 2 /2 - \sqrt 2 /3) + 9/4{\sin ^{ - 1}}(2\sqrt 2 /3)$

$= \sqrt 2 /6 + 9/4{\sin ^{ - 1}}(2\sqrt 2 /3)$ 

2. वक्रों ${(x - 1)^2} + {y^2} = 1$ एवं ${x^2} + {y^2} = 1$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : वक्र 

$= {({\text{x}} - 1)^2} + {{\text{y}}^2} = 1$

${\text{y}} = \sqrt 1  - {({\text{x}} - 1)^2}$ 

वृत्त का केंद्र $= (1,0)$

त्रिज्या \[ = {\mathbf{1}}\]

वक्र $= {x^2} + {y^2} = 1$

$y = \sqrt 1  - {x^2}$

वृत्त का केंद्र \[ = \left( {{\mathbf{0}},{\mathbf{0}}} \right)\]

त्रिज्या \[ = {\mathbf{1}}\]

दोनों वक्र मिलेंगे  ${x^2} = {(x - 1)^2}$

${2x = 1}$

${x = 1/2}$ 

क्षेत्रफल 

$= 2\left[ {\int_0^1 {^2} {y_1}dx + \int_1^1 {{q_2}} {y_2}dx} \right]$

$= 2\left\{ {\int_0 {_0^{12}} \sqrt 1  - {{({\text{x}} - 1)}^2}{\text{dx}} + \int_1^1 {_1} {{\text{q}}_2}\sqrt 1  - {{\text{x}}^2}{\text{dx}}} \right\}$

$= 2\left[ {(x - 1)/2\sqrt 1  - {{(x - 1)}^2} + 1/2{{\sin }^{ - 1}}(x - 1)/1} \right]_0^{112}$

$+ 2\left[ {x/2\sqrt {1 - {x^2}}  + 1/2{{\sin }^{ - 1}}x} \right]_1^1{\sigma _2} = 2\left[ {(1/2 - 1)/2\sqrt 1  - 1/4 + 1/2{{\sin }^{ - 1}}( - 1/2)( - 1/2)0 - 1/2{{\sin }^{ - 1}}( - 1)} \right]$

$+ 2\left[ {0 + 1/2{{\sin }^{ - 1}}(1) - 1/4\sqrt 1  - 1/4 - 1/2{{\sin }^{ - 1}}1/2} \right]$

$= 2[ - 1/4 \cdot \sqrt 3 /2 - 1/2 \cdot \pi /6 + 0 + 1/2 \cdot \pi /2] + \pi /2 - 1/2 \cdot \sqrt 3 /2 - \pi /6$

$=  - \sqrt 3 /4 - \pi /6 + \pi /2 + \pi /2 - \sqrt 3 /4 - \pi /6$

$= (2\pi /3 - \sqrt 3 /2)$ 

3. वक्रों $y = {x^2} + 2,y = x,x = 0$ एवं $x = 3$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : वक्र $y = {x^2} + 2$ और रेखा $x = 3$ मिलता है $(3,11)$ पर।

क्षेत्रफल 

$= \int_0^3 {\left( {{x^2} + 2} \right)} dx - \int_0^3 x dx$

$= \left[ {{x^3}/3 + 2x} \right]_0^3 - \left[ {{x^2}/2} \right]_0^3$

$= \left[ {{3^3}/3 + 6 - 0} \right] - \left[ {{3^2}/2 - 0} \right]$

$= 9 + 6 - 9/2$

$= 21/2$ 

4. समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष $( - 1,0),(1,3)$ एवं $(3,2)$ है।

उत्तर : मान लीजिए $A( - 1,0),B(1,3)$ और $C(3,2)$

$AB$ का समीकरण : $y - 0 = (3 - 0)/1 + 1(x + 1)$

$y = 3(x + 1)/2$

${\text{BC}}$ का समीकरण: ${\text{y}} - 3 = (2 - 3)/3 - 1({\text{x}} - 1)$

$y =  - x/2 + 1/2 + 3y$

$=  - x/2 + 7/2$ 

$AC$ का समीकरण : $y - 0 = (2 - 0)/3 + 1(x + 1)$

$y = x/2 + 1/2$

क्षेत्रफल 

$= \int_{ - 1}^1 3 /2(x + 1)dx + \int_1^3 {( - x/2 + 7/2)} dx - \int_{ - 1}^3 {(x/2 + 1/2)} dx$

$= 3/2\left[ {{x^2}/2 + x} \right]_{ - 1}^1 + \left[ { - {x^2}/4 + 7x/2} \right]_1^3 - \left[ {{x^2}/4 + x/2} \right]_{ - 1}^3$ 

\[ = {\mathbf{3}}{\text{ }}/{\text{ }}{\mathbf{2}}\left[ {{\mathbf{1}}{\text{ }}/{\text{ }}{\mathbf{2}} + {\mathbf{1}} - {\mathbf{1}}{\text{ }}/{\text{ }}{\mathbf{2}} - \left( { - {\mathbf{1}}} \right)} \right] + \left[ { - {\mathbf{9}}{\text{ }}/{\text{ }}{\mathbf{4}} + {\mathbf{21}}{\text{ }}/{\text{ }}{\mathbf{2}} + {\mathbf{1}}{\text{ }}/{\text{ }}{\mathbf{4}} - {\mathbf{7}}{\text{ }}/{\text{ }}{\mathbf{2}}} \right]\]

$ - [9/4 + 3/2 - 1/4 + 1/2]$

$= 3/2[2] + [7 - 2] - [2 + 2]$

$= 3 + 5 - 4$

$= 4$ 

5. समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के समीकरण $y = 2x + 1,y = 3x + 1$ एवं $x = 4$ हैं।

उत्तर : त्रिभुज के भुजाओं का समीकरण :\[{\mathbf{y}} = {\mathbf{2}}{\text{ }}{\mathbf{x}} + {\mathbf{1}},{\text{ }}{\mathbf{y}} = {\mathbf{3}}{\text{ }}{\mathbf{x}} + {\mathbf{1}},{\text{ }}{\mathbf{x}} = {\mathbf{4}}\]

त्रिभुज का शीर्ष : 

${\text{A}}(0,1),{\text{B}}(4,13),{\text{C}}(4,9)$

$= \int_0^4 {(3x + 1)} dx - \int_0^4 {(2x + 1)} dx$

$= \left[ {3{x^2}/2 + x} \right]_0^4 - \left[ {{x^2} + x} \right]_0^4$

$= 3 \times {4^2}/2 + 4 - 0 - \left[ {{4^2} + 4 - 0} \right]$

$= 24 + 4 - 20$

$= 8$ 

6. वृत्त ${x^2} + {y^2} = 4$ एवं रेखा $x + y = 2$ से घिरे छोटे भाग का क्षेत्रफल है:

(a) $2(\pi  - 2)$

(b) $\pi  - 2$

(c) $2\pi  - 1$

(d) $2(\pi  + 2)$

उत्तर : वृत्त $ = {x^2} + {y^2} = 4$, रेखा $ = x + y = 2$

$y = \sqrt 4  - {x^2}\quad y = 2 - x$

वृत्त और रेखा मिलते हैं ${\text{A}}(2,0)$ और ${\text{B}}(0,2)$ पर।

क्षेत्रफल 

$= \int_0^2 {\sqrt 4 }  - {x^2}dx - \int_0^2 {(2 - x)} dx$

$= \left[ {x/2\sqrt 4  + {x^2} + 4/2{{\sin }^{ - 1}}x/2} \right]_0^2 - \left[ {2x - {x^2}/2} \right]_0^2$

$= \left[ {2/2\sqrt 4  - 4 + 4/2{{\sin }^{ - 1}}(1) - 0 - 4/2{{\sin }^{ - 1}}(0)} \right] - [4 - 2]$

$= [2.\pi /2] - [4 - 2]$

$= (\pi  - 2)$ 

$(b)\pi  - 2$ उत्तर सही है |

प्रश्र 7. वक्रों ${{\text{y}}^2} = 4{\text{x}}$ एवं ${\text{y}} = 2{\text{x}}$ के मध्यवर्ती क्षेत्र का क्षेत्रफल:

(a) $2/3$

(b) $1/3$

(c) $1/4$

(d) $3/4$

उत्तर : वक्र ${y^2} = 4x,y = 2x$

दो वक्त मिलते हैं जहां ${(2x)^2} = 4x$

$4{x^2} - 4x = 0$

$4x(x - 1) = 0$

$x = 0,1$ 

जब,

$x = 0,y = 0$

तथा  \[{\mathbf{x}} = {\mathbf{1}},{\text{ }}{\mathbf{y}} = {\mathbf{2}}\]

क्षेत्रफल $= \int_0^1 {(2\sqrt x  - 2x)} {\text{dx}}$

$= \left[ {2{x^{3/2}}/3/2\quad  - {x^2}} \right]_0^1$

$= 4/3\quad {1^{3/2}} - {1^2} - 0$

$= 1/3$ 

\[\left( {\mathbf{b}} \right){\text{ }}{\mathbf{1}}{\text{ }}/{\text{ }}{\mathbf{3}}\] उत्तर सही है |

प्रश्नावली 8.3

1 . दिए हुए वक्रों एवं रेखाओं से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए :

(i) $y = {x^2},x = 1,x = 2$ एवं \[x{\text{ }} - \] अक्ष

उत्तर : प्रश्रानुसार परवलय $y = {x^2}$  का शीर्ष $(0,0)$ है और सममित रेखा $OY$ है।

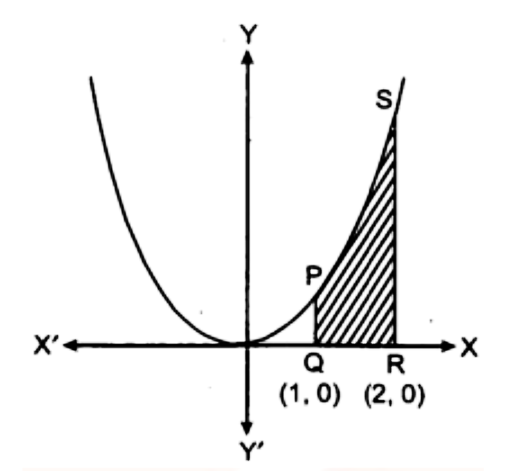
$y = {x^2},x = 1,x = 2x - $ अक्ष से घिरे क्षेत्र का क्षेत्रफल

क्षेत्र \[{\mathbf{PQRS}}\] का क्षेत्रफल 

$= \int_1^2 y dx$

$= \int_1^2 {{x^2}} dx$

$= \left[ {\frac{{{x^3}}}{3}} \right] = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}{\text{ }}$ वर्ग इकाई

(ii) $y = {x^4},x = 1,x = 5$ एवं \[x{\text{ }} - \] अक्ष

उत्तर : दिया है : $y = {x^4}$ बिन्दु $(0,0)$ से होकर जाता है। इसकी सममित रेखा $OY$ है।

${\text{y}} = {x^4},{\text{x}} = 1,{\text{x}} = 5$ एवं ${\text{x}} - $ अक्ष से घिरे क्षेत्र का क्षेत्रफल {क्षेत्र} \[{\mathbf{P}}{\text{ }}{\mathbf{Q}}{\text{ }}{\mathbf{R}}{\text{ }}{\mathbf{S}}\] { का क्षेत्रफल } 

$= \int_1^5 y dx$

$= \int_1^5 {{x^4}} dx$ 

$ = \left[ {\frac{{{x^5}}}{5}} \right] = 625 - \frac{1}{5} = \frac{{3124}}{5}${ वर्ग इकाई }

2. बक़ों $y = x$ एवं $y = {x^2}$ के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।

उत्तर : $y = x$ का मान $y = {x^2}$ में रखने पर

${x = {x^2}}$

${{x^2} - x = 0}$

${x(x - 1) = 0}$ 

$x = 0,1$

जब $x = 0$ तो $y = 0$ तथा जब $x = 1$ तो$y = 1$.

अतः $y = x$ एवं $y = {x^2}$  बिन्दु $(0,0)$ तथा $(1,1)$ पर प्रतिच्छेद करते हैं।

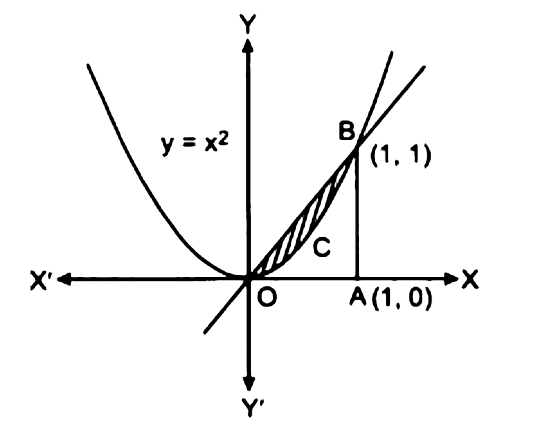
क्षेत्र का क्षेत्रफल $ = $ क्षेत्र $OCB$ का क्षेत्रफल

क्षेत्र \[{\mathbf{O}}{\text{ }}{\mathbf{A}}{\text{ }}{\mathbf{B}}\]  का क्षेत्रफल - क्षेत्र \[{\mathbf{0}}{\text{ }}{\mathbf{A}}{\text{ }}{\mathbf{B}}{\text{ }}{\mathbf{C}}\] का क्षेत्रफल  

$= \int_0^1 x dx - \int_0^1 {{x^2}} dx$

अभीष्ट क्षेत्रफल 

$= \int_0^1 x dx - \int_0^1 {{x^2}} dx$

$= \left[ {\frac{{{x^2}}}{2}} \right] - \left[ {\frac{{{x^2}}}{2}} \right]$ 

$= \frac{1}{2} - \frac{1}{3}$

$= \frac{1}{6}$ 

3. प्रथम चतुर्थाश में सम्मिलित एवं, $y = 4{x^2},x = 0,y = 1$ तथा $y = 4$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दिया है : $y = 4{x^2}$ एक परवलय जिसका शीर्ष $(0,0){\text{ }}$है। 

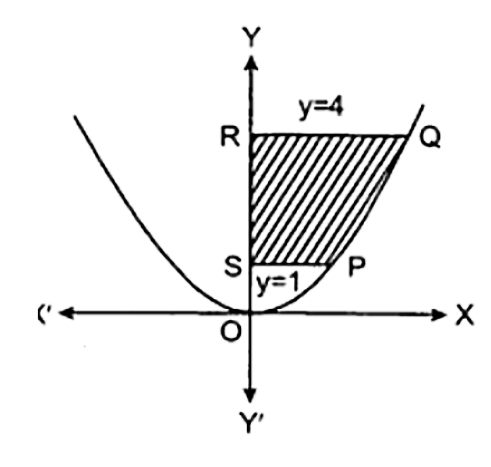
अब $y = 4{x^2},x = 0,y = 1$ तथा $y = 4$  से घिरे क्षेत्र का क्षेत्रफल

क्षेत्र \[{\mathbf{P}}{\text{ }}{\mathbf{Q}}{\text{ }}{\mathbf{R}}{\text{ }}{\mathbf{S}}\] का क्षेत्रफल 

$= \int_1^4 x dy$

$= \int_1^4 {\sqrt {\frac{y}{4}} } dy$

$= \frac{1}{2}\int_1^4 {\sqrt y } dy$

$= \frac{1}{2} \times \frac{2}{3}\left[ {{y^{\frac{3}{2}}}} \right]$ 

$= \frac{1}{3} \times \left[ {{4^{\frac{3}{2}}} - 1} \right] = \frac{7}{3}$वर्ग इकाई

4. $y = |x + 3|$ का ग्राफ खींचिए एवं $\int_{ - 6}^0 | x + 3|dx$ का मान ज्ञात कीजिए।

उत्तर : 

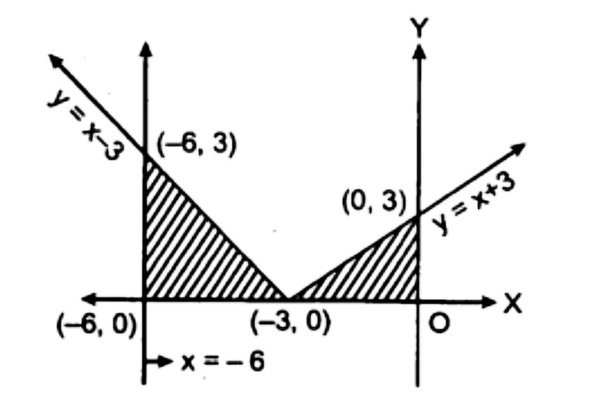
$\int_{ - 6}^0 | {\text{x}} + 3|{\text{dx}} = $क्षेत्र ${\text{PQRS}}$ का क्षेत्रफल 

क्षेत्र ${\text{ABC}}$ का क्षेत्रफल $ + $ क्षेत्र ${\text{CDE }}$का क्षेत्रफल 

$= \frac{1}{2} \times (6 \times 3) + \frac{1}{2} \times (3 \times 3)$

$= 9 + \frac{9}{2} = \frac{{27}}{2}{ वर्ग इकाई। }$

5. $x = 0$ एवं $x = 2\pi $ तथा वक़$y = \sin (x)$, से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : $y = \sin (x)$ के ग्राफ निम्नानुसार प्राप्त होता है :

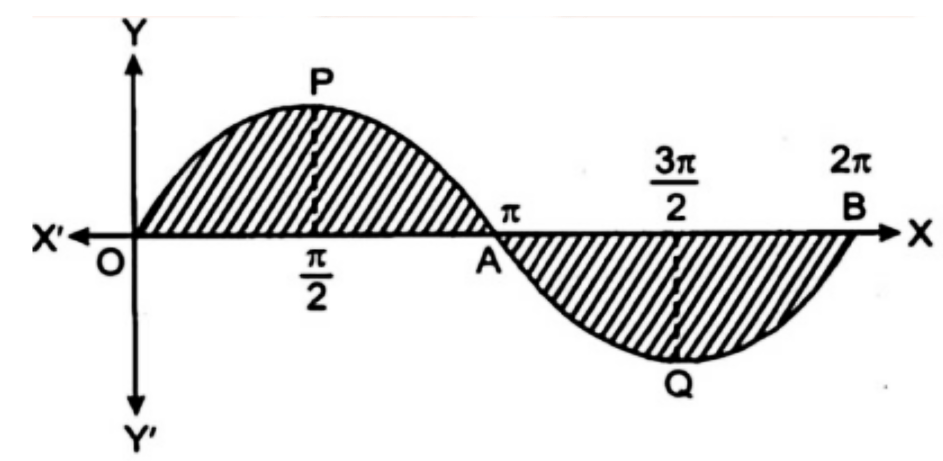
अभीष्ट क्षेत्रफल $= \int_0^\pi  y dx - \int_\pi ^{2\pi } y dx{\text{ }}$

$= \int_0^\pi  {\sin } (x)dx - \int_\pi ^{2\pi } {\sin } (x)dx\quad $

$= ( - ( - 1) + 1) + ( - ( - 1) + 1)$ 

$=4$ वर्ग इकाई

6. परवलय ${y^2} = 4{\text{ax}}$ एवं रेखा $y = mx$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : \[{\mathbf{y}} = {\mathbf{m}}{\text{ }}{\mathbf{x}}\] का मान समीकरण

(i) में रखने पर

${m^2}{x^2} = 4{\text{ax or x}} = \frac{{4a}}{{{m^2}}}{\text{ and x}} = 0$

इस प्रकार वक्र ${y^2} = 4ax$ और रेखा $y = mx$ बिन्दु $0(0,0)$ तथा ${\text{P}}\left( {\frac{{4a}}{{{m^2}}},\frac{{4a}}{{{m^2}}}} \right)$ पर प्रतिच्छेद करते

अत; 

${y^2} = 4ax$

$y = mx$ 

से घिरे क्षेत्र का क्षेत्रफल

क्षेत्र $OCB$ का क्षेत्रफल 

क्षेत्र $ABCO$ का क्षेत्रफल $ - {\text{ }}OAB{\text{ }}$का क्षेत्रफल 

$= \int_0^{\frac{{4a}}{{{m^2}}}} {\sqrt {4ax} } dx - \int_0^{\frac{{4a}}{{{m^2}}}} m xdx$

$= \frac{{8{a^2}}}{{3{m^3}}}$ 

7. परवलय $4y = 3{x^2}$ एवं रेखा $2y = 3x + 12$  से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : \[{\mathbf{2}}{\text{ }}{\mathbf{y}} = {\mathbf{3}}{\text{ }}{\mathbf{x}} + {\mathbf{12}}\] का मान समीकरण (6) में रखने पर

$2(3x + 12) = 3{x^2}$

$3{x^2} - 6x - 24 = 0$ 

$(x - 4)(x + 2) = 0$

$x = 4,x =  - 2$ 

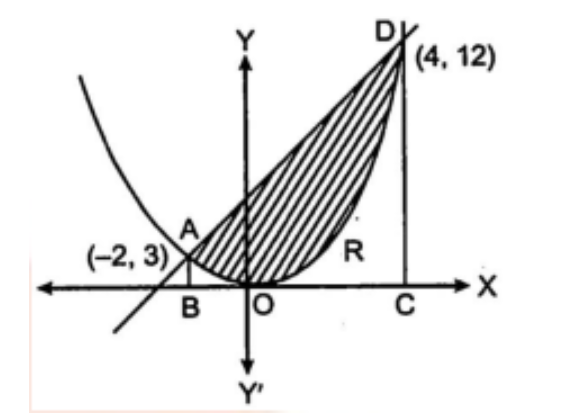
इस प्रकार परवलय और रेखा एक-दूसरे को $P( - 2,3)$ तथा $Q(4,12)$ पर प्रतिच्छेद करते हैं।

अभीष्ट क्षेत्रफल $ = $ क्षेत्र $AOD$ का क्षेत्रफल

= समलम्ब चतुर्भुज $ABCD$ का क्षेत्रफल - क्षेत्रफल $ABCDA$

$= \int_{ - 2}^4 y 1dx - \int_{ - 2}^4 y 2dx$

$= \frac{1}{2}\int_{ - 2}^4 {(3x + 12)} dx - \int_{ - 2}^4 {\frac{{3{x^2}}}{4}} dx$

$= \frac{1}{2}(24 + 48) - (6 - 24) - \frac{3}{4}\left( {\frac{{64}}{3} - \left( { - \frac{8}{3}} \right)} \right)$ 

$= 27$ वर्ग इकाई

8. दीर्घवृत्त $\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$ एवं रेखा $\frac{x}{3} + \frac{y}{2} = 1$ से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दोनों समीकरणों से प्राप्त बिन्दु \[{\mathbf{4}}\left( {{\mathbf{3}},{\mathbf{0}}} \right),{\text{ }}{\mathbf{8}}\left( {{\mathbf{0}},{\mathbf{2}}} \right)\] एक दूसरे को प्रतिच्छेद करते हैं।

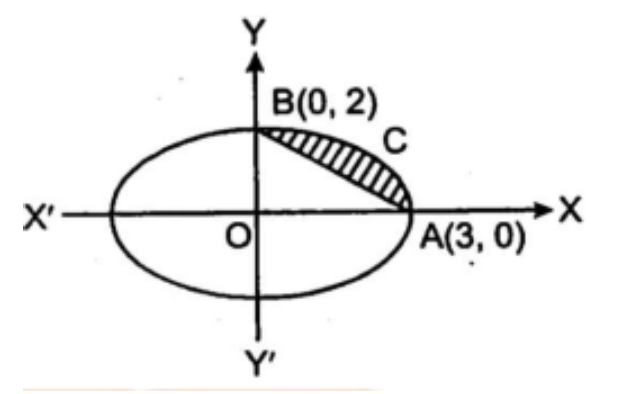
अभीष्ट क्षेत्रफल $= \int_0^3 y 1dx$ (दीर्ष वृत्त के लिए) - $\int_0^3 y 2dx$ रेखा के लिए)

$= \frac{3}{2}\int_0^3 {\sqrt {9 - {x^2}} } dx{\text{  -  }}\int_0^3 {\left( {1 - \frac{x}{3}} \right)} dx$

$= \frac{3}{2}(\pi ) - \frac{2}{3}\left( {\frac{9}{2}} \right)$

$= \frac{3}{2}\pi  - 3$ 

$= \frac{3}{2}(\pi  - 2)$ { वर्ग इकाई}

9. दीर्घवृत्त $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ एवं रेखा $\frac{x}{a} + \frac{y}{b} = 1$ से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दोनों समीकरण बिन्दु ${\text{A}}({\text{a}},0)$ तथा ${\text{B}}(0,\;{\text{b}})$ पर प्रतिच्छेद करते हैं।

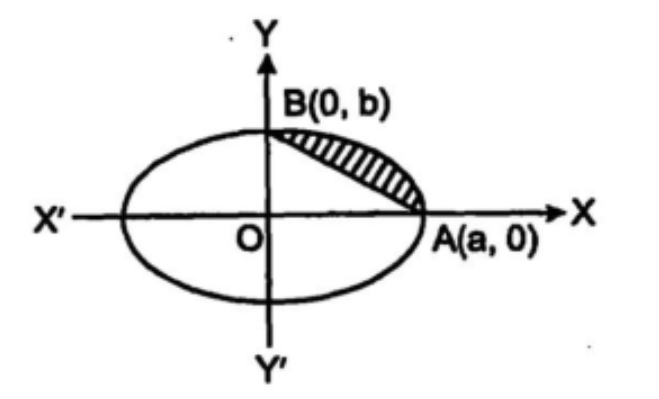
अभीष्ट क्षेत्रफल $ = $ क्षेत्र $BAC$ का क्षेत्रफल $ = $ क्षेत्र $OACB$ का क्षेत्रफल - क्षेत्र $OAB$ का क्षेत्रफल

$= \frac{b}{a}\int_0^a {\sqrt {{a^2} - {b^2}} } dx - \int_0^a {\left( {1 - \frac{x}{a}} \right)} dx$

$= \frac{b}{a}\left( {\frac{{{a^2}}}{2}{{\sin }^{ - 1}}(1) - 0} \right) - \frac{b}{a}\left( {\frac{{{a^2}}}{2}} \right)$

$= \frac{{ab\pi }}{4} - \frac{{ba}}{2}$

$= \frac{{ab}}{4}(\pi  - 2)$ 

10. परवलय ${x^2} = y$  रेखा $y = x + 2$ और \[x{\text{ }} - \] अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : समीकरण (i) तथा (ii)

${x^2} = x + 2{x^2} - x - 2 = 0$

$(x - 2)(x + 1) = 0$

$x = 2, - 1$ 

जब $x = 2\quad y = 4$

और जब $x =  - 1\quad y = 1$

अत: बिन्दु $(2,4),( - 1,1)$प्रतिच्छेदन बिन्दु हैं।

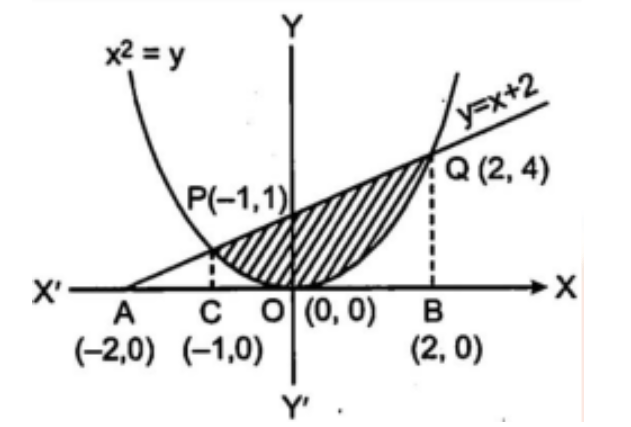
अभीष्ट क्षेत्रफल $= \int_{ - 1}^2 y 1dx - \int_{ - 1}^2 y 2dx$

$= \int_{ - 1}^2 {\left( {{x^2} + 2 - x} \right)} dx$

$= \frac{3}{2} + 6 - 3 = \frac{9}{2}$ वर्ग इकाई

11. समाकलन विधि का उपयोग करते हुए बक़ $|x| + |y| = 1$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : समाकलन:

$x + y = 1$

$x - y = 1$ 

$- x + y = 1$

$- x - y = 1$ 

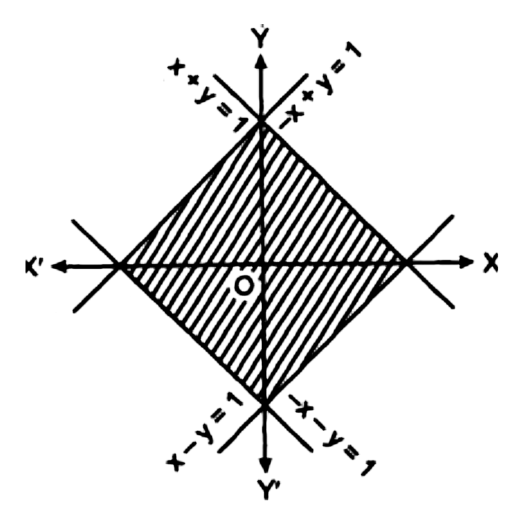
इनसे घिरे क्षेत्र का अभ्यस्त क्षेत्रफल =

$= 4\int_0^1 y dx$

क्योंकि आकृति \[{\mathbf{x}}{\text{ }} - \]अक्ष तथा \[{\mathbf{y}} - \] अक्ष के लिए सममित है

$\quad  = 4\int_0^1 {(1 - x)} dx$

$= 4\left( {x - \frac{{{x^2}}}{2}} \right)$

$= 4 \times \frac{{1/2}}{{}}$ 

$= 2{\text{ }}$ वर्ग इकाई

12. वक्रों $\left\{ {(x,y):{x^2} < y,y = |x|} \right\}$ तथा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दिया है : वक्र एक परवलय है जिसका शीर्ष $(0,0)$ है तथा सममित अक्ष $OY$ है।

समीकरण $y = |x|$ दो रेखाओं को निरूपित करता है।

जब $x > 0$ तो $y = x$ तथा जब$x < 0,y =  - x$.

अर्थात् $y = x,{x^2} = y$ को $(0,0),(1,1)$ पर प्रति

और $y =  - x,{x^2} = y\quad $को $(0,0),( - 1,1)$

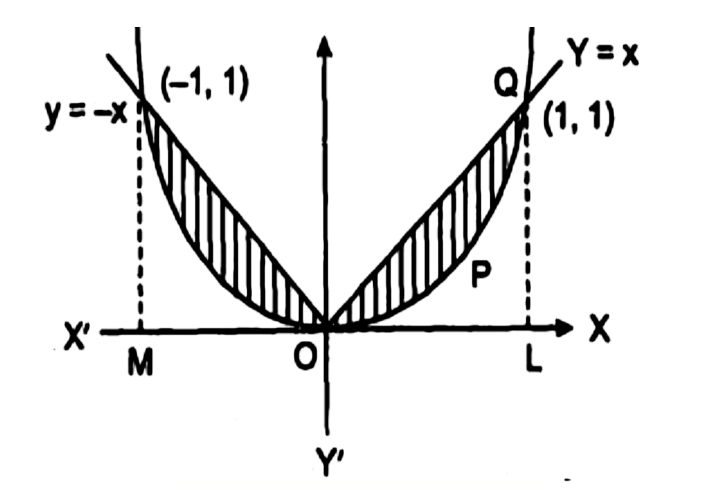
अतः अभीष्ट क्षेत्रफल \[ = {\mathbf{2}}{\text{ }}{\mathbf{X}}\] क्षेत्र ${\text{OPQ}}$ का क्षेत्रफल $ = 2 \times [{\text{QLO}}$का क्षेत्रफल - क्षेत्र

$= 2\left[ {\int_0^1 y 1dx - \int_0^1 y 2dx} \right]$

$= 2\left[ {\int_0^1 x dx - \int_0^1 {{x^2}} dx} \right]$

$= 2\left\{ {\left[ {\frac{{{x^2}}}{2}} \right]_0^1 - \left[ {\frac{{{x^3}}}{3}} \right]_0^1} \right\}$

$= 2 \times \frac{1}{6}$

$= \frac{1}{3}{\text{  }}$ 

वर्ग इकाई

13. समाकलन विधि का उपयोग करते हुए, एक ऐसे त्रिभुज $ABC$ क्र क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक $A(2,0),B(4,5)$ एवं $C(6,3)$ हैं।

उत्तर : दिया है : रेखा $AB$ का समीकरण

$y - 0$

$= \frac{{5 - 0}}{{4 - 2}}(x - 2)$

$= \frac{5}{2}(x - 2)$ 

अर्थात् इसी प्रकार रेखा $BC$ का समीकरण है

$y - 5 = \frac{{3 - 5}}{{6 - 4}}(x - 4)$

$y =  - x + 9$ 

तथा रेखा $CA$ का समीकरण है

$y - 5 = \frac{{0 - 3}}{{2 - 6}}(x - 6)$

$4y = 3x - 6$ 

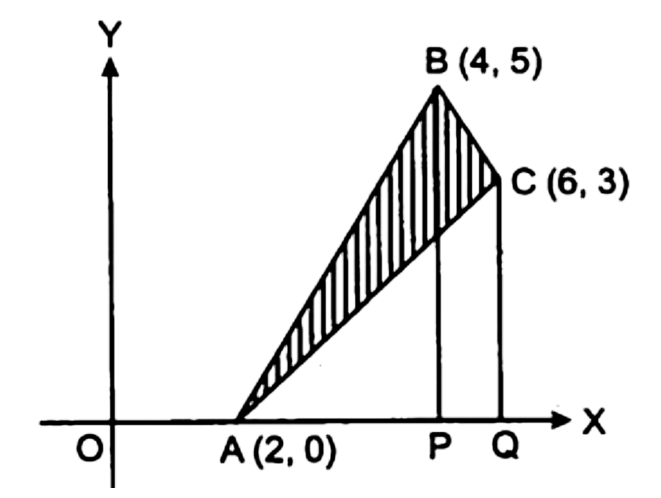
अभीष्ट क्षेत्रफल $ = ABC$ द्वारा घेरा गया क्षेत्र का क्षेत्रफल $ = {\text{APB}}$ क्षेत्र का क्षेत्रफल + समलम्ब चतुर्भुज ${\text{BPQC}}$ का क्षेत्रफल - क्षेत्र ${\text{AQC}}$ का क्षेत्रफल

$= \frac{5}{2}\int_2^4 {(x - 2)} dx + \int_4^6 {( - x - 9)} dx - \frac{3}{4}\int_2^6 {(x - 2)} dx$

\[\left. { = \frac{5}{2}{\text{ }}\left[ {\frac{{{{(x - 2)}^2}}}{2}} \right]_2^4 + \left[ {\frac{{{{(x - 9)}^2}}}{2}} \right]_4^6 - \frac{3}{4}\left[ {\frac{{{{(x - 2)}^2}}}{2}} \right]} \right]_2^6\]
$ = 5 + 8 - 6 = 7$ { वर्ग इकाई। }

14. समांकलन विधि का उपयोग करते हुए, रेखाओं $2x + y = 4,3x - 2y = 6$ एवं $x - 3y + 5 = 0$से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर : दिए गए समीकरण हैं :

${{\mathbf{2}}{\text{ }}{\mathbf{x}} + {\mathbf{y}} = {\mathbf{4}}{\text{ }}}$ 

${{\mathbf{3}}{\text{ }}{\mathbf{x}} - {\mathbf{2}}{\text{ }}{\mathbf{y}} = {\mathbf{6}}}$

${{\mathbf{x}} - {\mathbf{3}},{\mathbf{y}} = {\mathbf{5}}}$

समीकरण (i) को \[{\mathbf{2}}\] से गुणा करके (ii) में जोड़ने पर

$7x = 14$ या \[{\mathbf{x}} = {\mathbf{2}}\]

अब समीकरण (i) में$x = 2$;

$4 + y = 4$ या \[{\mathbf{y}} = {\mathbf{0}}\]

अत: बिन्दु $C$ निर्देशांक$ = (2,0)$.

समीकरण (iii) को \[{\mathbf{2}}\] से गुणा करके समीकरण (i) में से घटाने पर $7y = 14$ या $y = 2$

पुनः समीकरण (i) से $2x + 2 = 4$ या $x = 1$

अतः बिन्दु $A$ के निर्देशांक $= (1,2)$

समीकरण (iii) को \[{\mathbf{3}}\] से गुणा करके समीकरण (i) में घटाने पर,

$7y = 21$

$\Rightarrow y = 3$ 

अब समीकरण (ii) से $3x - 6 = 6$ या $x = 4$

अतः बिन्दु $B$ के निर्देशांक $(4,3)$ हैं।

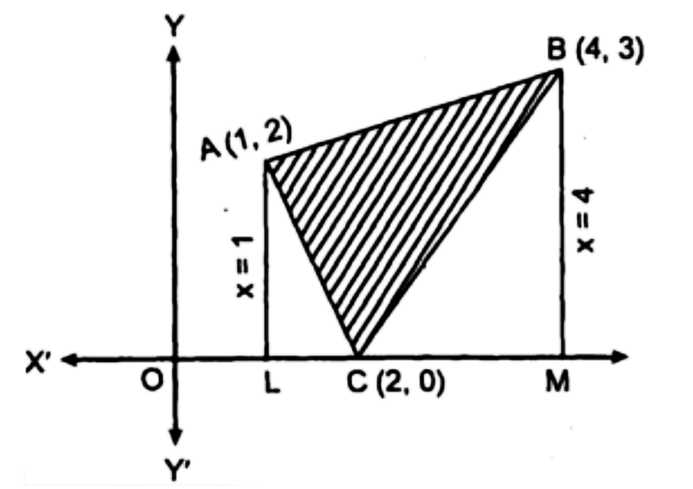
त्रिभुज $ABC$ का क्षेत्रफल = समलम्ब चतुर्भुज \[{\mathbf{A}}{\text{ }}{\mathbf{L}}{\text{ }}{\mathbf{M}}{\text{ }}{\mathbf{B}}\] का क्षेत्रफल ${\text{ALC}}$ का क्षेत्रफल $ - {\text{BCM}}$ का क्षेत्रफल

$= \int_1^4 {\frac{{(x + 3)}}{3}} dx - \int_1^2 {(4 - 2x)} dx - \int_2^4 {\frac{{3x - 6}}{2}} dx$

$= \frac{1}{3}\left[ {\frac{{{{(x)}^2}}}{2} + 5x} \right]_1^4 - \left[ {4x - {x^2}} \right]_1^2 - \frac{1}{2}\left[ {\frac{{3{x^2}}}{2} - 6x} \right]_2^4$

$= \frac{1}{3}\left[ {28 - \frac{{11}}{2}} \right] - [4 - 3] - \frac{1}{2}(0 + 6)$

$= \frac{1}{3} \times 45/2 - 1 - 3$ 

$= 15/2 - 4 = 7/2\quad ${ वर्ग इकाई। }

15. क्षेत्र $\left\{ {(x,y):{x^2} < 4x,4{x^2} + 4{y^2} < 9} \right\}$ का क्षेत्रफल ज्ञात कीजिए।

उत्तर : समीकरण (i) तथा (ii) को हल करने पर. $A\left( {\frac{1}{2},\sqrt 2 } \right)$और ${\text{B}}\left( {\frac{1}{2}, - \sqrt 2 } \right)$ पर होते हैं। दोनों ही वक्र ${\text{x}} -$ अक्ष के सापेक्ष सममित हैं।

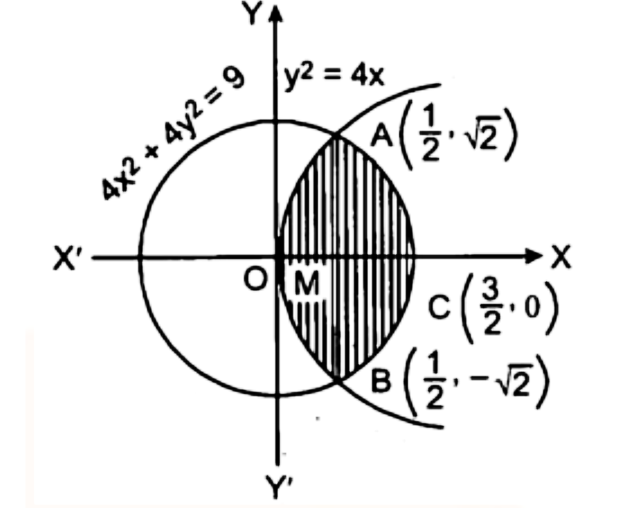
अभीष्ट क्षेत्रफल = छायांकित भाग का क्षेत्रफल

$= 2\left( {\int_0^{\frac{1}{2}} 2 \sqrt x dx + \int_{\frac{1}{2}}^{\frac{3}{2}} {\sqrt {\frac{9}{4}} }  - {x^2}{\text{dx}}} \right)$

$= 2\left[ {\frac{{{x^{\frac{3}{2}}}}}{{\frac{1}{3}}}} \right]_0^{\frac{1}{2}} - 2\left[ {\frac{x}{2}\sqrt {\frac{9}{4} - {x^2}}  + \frac{9}{4}\frac{1}{2}{{\sin }^{ - 1}}\left( {\frac{{2x}}{3}} \right)} \right]$

$= \frac{{2\sqrt 2 }}{3} + \frac{9}{4}{\sin ^{ - 1}}(1) - \left( {\frac{1}{2}\sqrt 2  + \frac{9}{4}{{\sin }^{ - 1}}\frac{1}{3}} \right)$

$= \frac{{2\sqrt 2 }}{3} - \frac{{\sqrt 2 }}{2} + \frac{9}{4}\frac{\pi }{2} - \frac{9}{2}{\sin ^{ - 1}}\left( {\frac{1}{3}} \right)$

$= \frac{{9\pi }}{8} - \frac{9}{4}{\sin ^{ - 1}}\left( {\frac{1}{3}} \right) + \frac{1}{{3\sqrt 2 }}$ 

16 से 19 तक के प्रश्रों में सही उत्तर का चयन कीजिए-

16. $y = {x^3},x - $ अक्ष एवं कोटियों $x =  - 2,x = 1$ से घिरे क्षेत्र का क्षेत्रफल है-

(A) $ - 9$

(B) $ - \frac{{ - 15}}{4}$

(C) $\frac{{15}}{4}$

(D) $\frac{{17}}{4}$

उत्तर : दिया गया वक्र $y = {x^ \wedge }3$

${\text{dy}}/{\text{dx}} = 3{{\text{x}}^ \wedge }2 = $ घनात्मक है।

दिया गया वक्र वद्धमान है,

$dy/dx = 0,x = 0$

\[{\mathbf{X}} - \] अक्ष पर स्पर्श रेखा है,

$f( - x) =  - f(x),{( - x)^ \wedge }3 =  - {x^ \wedge }3$

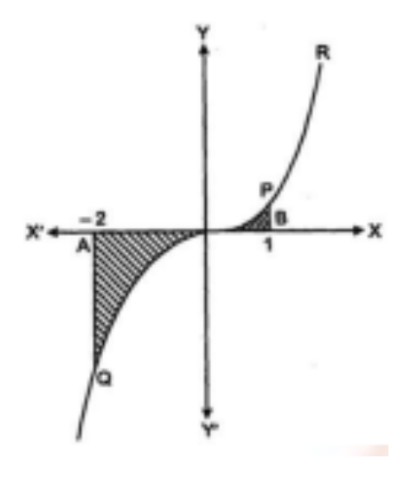
$y = {x^ \wedge }3$ द्वारा घिरे क्षेत्र का क्षेत्रफल $ = AQOA$ का क्षेत्रफल $ + BPO$ का क्षेत्रफल

$= \int {{x^ \wedge }} 3dx + \int {{x^ \wedge }} 3dx$

$= \left[ {0 - {{( - 2)}^ \wedge }4/4} \right] + [1/4 - 0]$

$= 16/4 + 1/4$

$= 17/4$ 

(D) $17/4$ उत्तर सही है |

17, बक़ \[y = x\left| x \right|,{\text{ }}x{\text{ }} - \] अक्ष एवं कोटियों $x =  - 1$ तथा $x = 1$ से घिरे क्षेत्र का क्षेत्रफल है :

(A) \[0\]

(B) $\frac{1}{3}$

(C) $\frac{2}{3}$

(D) $\frac{4}{3}$

उत्तर : जब $x > 0,|x| = x$

दिया गया वक्र का समीकरण है : 

$y = {x^ \wedge }2$

$y =  + {x^ \wedge }2$ 

जब $x < 0,|x| =  - x$

दिया गया वक्र का समीकरण है : $y =  - {x^ \wedge }2$

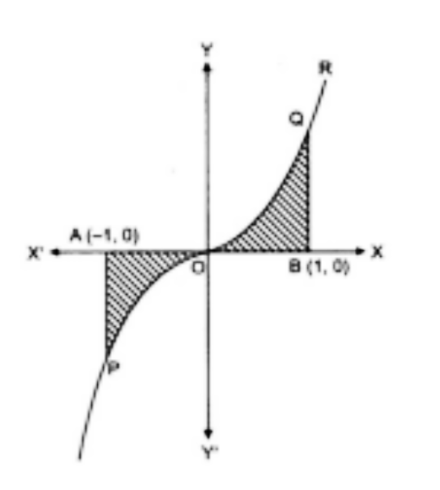
\[{\mathbf{x}} - \]अक्ष से घिरा क्षेत्रफल $ = POA$ का क्षेत्रफल $ + BQO$ का क्षेत्रफल

$= \int  -  {x^ \wedge }2dx + \int {{x^ \wedge }} 2dx$

$= 2\int {{x^ \wedge }} 2dx$

$= 2\left[ {{x^ \wedge }3/3} \right]$

$= 2/3$ 

(C) $2/3$ उत्तर सही है |

18. क्षेत्र ${y^2} >  = 6x$और वृत्त ${x^2} + {y^2} = 16$ में सम्मिलित क्षेत्र का क्षेत्रफल है :

(A) $\frac{4}{3}(4\pi  - \sqrt 3 )$

(B) $\frac{4}{3}(4\pi  + \sqrt 3 )$

(C) $\frac{4}{3}(8\pi  - \sqrt 3 )$

(D) $\frac{4}{3}(4\pi  + \sqrt 3 )$

उत्तर : वक्र का समीकरण है:

${x^ \wedge }2 + {y^ \wedge }2 = 16{y^ \wedge }2 = 6x$

समीकरण (i) में ${y^ \wedge }2 = 6x$ रखने पर

${x^ \wedge }2 + 6x = 16$

${x^ \wedge }2 + 6x - 16 = 0$

$(x + 8)(x - 2) = 0$

$x =  - 8,2$ 

परवलय तथा वृत्त के अंदर का क्षेत्रफल $ = POQAP$ का क्षेत्रफल

$x \ne  - 8$

$x = 2$ 

$ = 2({\text{POM}}$का क्षेत्रफल $ + {\text{PMA}}$का क्षेत्रफल)

$= 2\left[ {\int {\sqrt 6 } xdx + \int {\left( {\sqrt {16}  - {x^ \wedge }2} \right)} dx} \right]$

$= 2\left[ {\sqrt 6  \cdot 2/3\left[ {{x^ \wedge }3/2} \right] + \left[ {x/2\sqrt {\left. {\left( {16 - {x^ \wedge }2} \right) + 16/2{{\sin }^ \wedge } - 1x/4} \right]} } \right.} \right.$

$= 4\sqrt {3/3 + 16\pi /3}$ 

अब वृत्त ${x^ \wedge }2 + {y^ \wedge }2 = 16$  का क्षेत्रफल

$= 4\int {\sqrt {\left( {16 - {x^ \wedge }2} \right)} } dx$

$= 4[x\sqrt {\left. {\left( {16 - {x^ \wedge }2} \right)/2 + 8{{\sin }^ \wedge } - 1x/4} \right]}$ 

$= 16\pi $

अभीष्ट क्षेत्रफल 

$= 16\pi  - (4\sqrt 3 /3 + 16\pi /3)$

$= 4/3(8\pi  - 3)$ 

(C) $4/3(8\pi  - 3)$ उत्तर सही है |

19. \[y{\text{ }} - \] अक्ष, $y = \cos (x)$ एवं $y = \sin (x);0 \leqslant x \leqslant \frac{\pi }{2}$ से घिरे क्षेत्र का क्षेत्रफल है -

(A) $2(\sqrt 2  - 1)$

(B) $\sqrt 2  - 1$

(C) $\sqrt 2  + 1$

(D) $\sqrt 2 $

उत्तर : \[{\mathbf{y}}\] का मान रखने पर, $\sin x = \cos x$

या $\tan x = 1$

या $x = \pi /4$

$\sin \pi /4 = \cos \pi /4 = 1/\sqrt 2 $

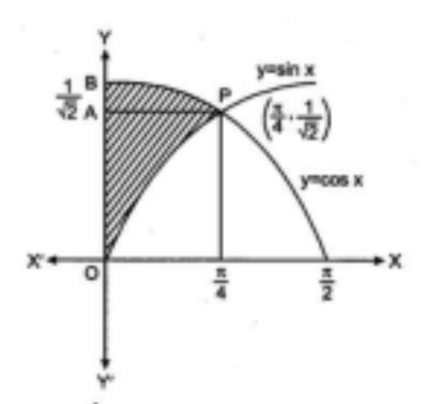
\[{\mathbf{y}} - \] अक्ष पर, $y = \cos x$ तथा $y = \sin x = OPBO$ का क्षेत्रफल 

$= {\text{PAO}}$  का क्षेत्रफल $ + {\text{APBA}}$ का क्षेत्रफल 

$= \int x 1dy + \int x 2dy$

जहाँ $\times 1$ वक्र $y = \sin x$ या $x = {\sin ^ \wedge } - 1y$

और $\times 2$ वक्र $y = \cos x$ या $x = {\cos ^ \wedge } - 1y$

$= \int {{{\sin }^ \wedge }}  - 1ydy + \int {{{\cos }^ \wedge }}  - 1ydy$

$= (1/\sqrt 2 *\pi /4 + 1/\sqrt 2  - 1) + (0 - 1/\sqrt 2 *\pi /4 + 1/\sqrt 2 )$

$= 2*1/\sqrt 2  - 1$

$= \sqrt 2  - 1$ 

(B) $\sqrt 2  - 1$ उत्तर सही है |

NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 12 Maths Chapter 8 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 12 Maths Chapter 8 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 12 Maths Chapter 8 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 12 Maths Application of Integrals solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 12 Maths Application of Integrals in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 12 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 12 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.