NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments - FREE PDF Download



FAQs on NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
1. Where can I get Solutions for Ray Optics Class 12?
Students can get Ray Optics class 12 NCERT solutions online on the website of Vedantu. It is downloadable for free. The solutions are provided in a simple manner with a clear explanation of concepts. Here students will find answers to all the NCERT questions.
The answers have been written by subject matter experts, to help students. Students will find accurate answers along with, illustrations, diagrams, comparison tables, and pictures in the explanation of every solution. The Ray optics class 12 NCERT solutions PDF is the best guide for every student when it comes to clearing of doubts. If students are pressed for time they can easily refer to the solutions given here thereby cutting their revision time by half.
2. How can I Study for Ray Optics Class 12?
Firstly, when it comes to studying anything remember that studying it three times helps. Three is the magic number you have to target. Once three revisions have been completed, work on the exercises at the back of the chapter. The Ray optics class 12 NCERT solutions will help students if they get stuck in any of the problems. The solutions are written in a lucid, practical style with diagrams and illustrations wherever necessary. Ray diagrams are drawn to explain the key points. Students will also find it helpful to go through past year papers and sample questions. They will need to practice ray diagrams for convex and concave mirrors if they want to score well. Ray Optics class 12 NCERT solutions PDF will help students in their exam preparation.
3. What is the Meaning of Ray Optics?
Ray optics deals with the propagation of light through media like a convex and concave lens. Some of the other topics covered in this chapter are refraction, mirror equation, and focal length of spherical mirrors. Additionally, three important phenomena of light are observed, namely, refraction, dispersion, and reflection. Students who are facing difficulty with Ray Optics class 12 NCERT should download and consult the Ray Optics class 12 solutions. This will benefit them greatly. Their conceptual understanding will improve by going through the solved questions. They will have a chance to compare, identify, and correct their mistakes by referring to the solutions.
4. What are the important topics of Class 12 Physics Chapter 9 Ray Optics and Optical Instruments?
Ray Optics is a vast and difficult chapter which requires proper guidance to understand each and every topic properly. Vedantu provides NCERT SOlutions to help students understand the chapter better and solve the questions based on the chapter effortlessly. In case students have any doubts, they can also refer to the online notes created by expert teachers at Vedantu. Students can also register for online classes where they can interact with the teacher and clear their doubts right away. A few of the important topics in the chapter are:
Total Internal Reflection
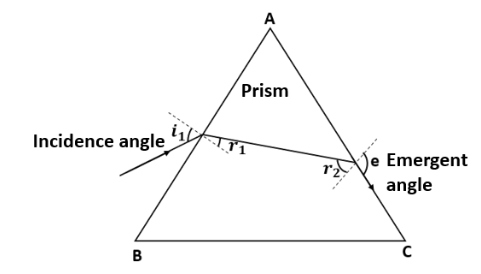
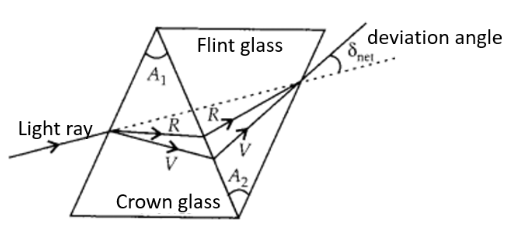
Refraction Through A Prism
Image formation by spherical lenses
Image formation by spherical mirrors
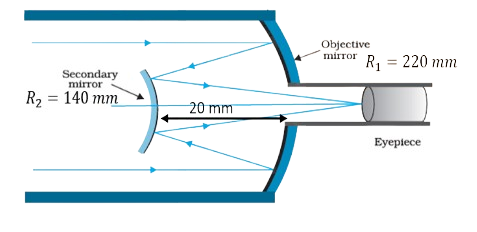
Telescope
Microscope
Eye
Natural Phenomena Due to Light
Power combination of lenses
5. What type of questions are asked from optics in the board exam?
Optics is a very important chapter for the Class 12 board exam as well as future reference and preparation of competitive exams. There are a few crucial topics that you definitely cannot afford to miss in the Chapter. Reflection of Light, Spherical Mirrors, Refraction of Light, Prism, Simple Microscope, Telescope, Lens and Optical Instruments are some of the important topics of the chapter. The type of questions asked from this chapter in board exams includes numerical and definitions.
You can find the important questions for exam purposes from Vedantu's website, which will definitely help you to understand the types of questions usually asked in the board exams for class 12 Physics Chapter ray optics.
6. Is Ray Optics important for NEET?
Going by the chapter wise distribution of weightage for the NEET exam, approximately 5% of the total questions in the question papers of the past eight years have been asked from Ray Optics. A few important topics are:
Reflection
Refraction Through A Glass Slab
Total Internal Reflection
Refraction Through Spherical Surfaces And Lenses
Refraction, Dispersion Through A Prism
The Human Eye
Microscopes and Telescopes
7. What is the difference between ray optics and wave optics?
The main point of difference between Ray optics and Wave optics is:
Ray optics works with light as it travels in the path of a line, refracts from a given surface or reflects from it, and later continues as a straight line towards other surfaces.
Wave optics is used as a standard to analyse the propagation of light when there exist a lot of photons.
You can learn in detail about the differences between the two topics from Vedantu's NCERT solutions for class 12 Physics Chapter 9, ray optics.
8. What are the most important topics in Ray Optics?
The most important topics in Ray optics are as follows:
Application Of Refraction
Total Internal Reflection
Derivation Of Prism Refractive Index Formula
Derivation Of Refraction At A Spherical Surface
Applications Of Scattering
Rayleigh Criteria
A good idea is to follow the NCERT solutions PDF provided by Vedantu to understand and take note of these important concepts to have a sure shot chance of scoring well in the exams.
9. What are optics and their types?
The discipline that studies the properties of a wave of light is called Optics. Optics can be further divided into three major subtypes:
Interference
Diffraction
Polarisation
One can access more about these topics on the Vedantu website and get all the required information free of cost and also utilise the Vedantu Mobile App.
10. What is the purpose of ray optics discussed in Ray Optics Class 12 NCERT Solutions?
Ray optics, also known as geometrical optics, studies the behaviour of light by treating it as a collection of rays. It helps us understand phenomena like reflection, refraction, and image formation by lenses and mirrors using geometric principles.
11. How many hours to complete Ray Optics NCERT Solutions?
The time to complete this chapter depends on your learning pace and background. It can take anywhere from a few hours to a week or more. Focus on understanding the concepts, solving practice problems, and referring to the NCERT solutions for clarification.
12. What is important in Class 12 Physics Chapter 9 Exercise Solutions?
Here are some key things to understand in ray optics:
Laws of reflection and refraction
Sign conventions for mirrors and lenses (focal length, object/image distance)
Mirror and lens equation for image formation
Ray diagrams for reflection and refraction
Applications of lenses and mirrors in optical instruments
13. What are the advantages of Ray Optics mentioned in Class 12 Ray Optics NCERT Solutions?
Ray optics is a powerful tool because:
It's a simple approach to understanding light behaviour for many practical applications.
It helps design and analyses optical instruments like telescopes, microscopes, and eyeglasses.
It lays the foundation for more advanced optics concepts like wave optics.
14. What is a ray of light called?
A ray of light isn't a formal scientific term, but it's a convenient way to visualize the propagation of light as a straight line.
15. Is Ray Optics Class 12 Physics Ch 9 NCERT Solutions tough?
The difficulty depends on your maths and physics background. Class 12 Physics Ray Optics NCERT Solutions involve applying geometric concepts and algebraic equations. With a solid foundation and practice, you can grasp the concepts effectively.
16. How can NCERT Solutions Chapter 9 Physics Class 12 help me learn the key concepts of ray optics?
By going through solved problems in Class 12 Physics Chapter 9 NCERT Solutions, you see how formulas and principles are applied to various scenarios. This helps solidify your understanding of core concepts like reflection, refraction, mirror and lens equations, and image formation.
17. What are the main topics covered in Class 12 Physics Chapter Ray Optics NCERT Solutions?
The main topics covered in Ch 9 Physics Class 12 include:
Laws of reflection and refraction
Image formation by plane and spherical mirrors
Lens formula and magnification for convex and concave lenses
Optical instruments like microscopes and telescopes
Phenomena such as dispersion, total internal reflection, and the working principles of optical fibres