How Many Squares? - Exercise-wise Questions and Answers For Class 5 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 5 Maths Chapter 3 How Many Squares? - 2025-26
1. What concepts are covered in NCERT Solutions for Class 5 Maths Chapter 3 How Many Squares?
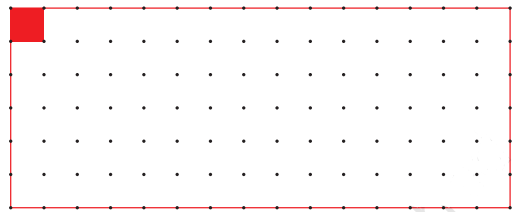
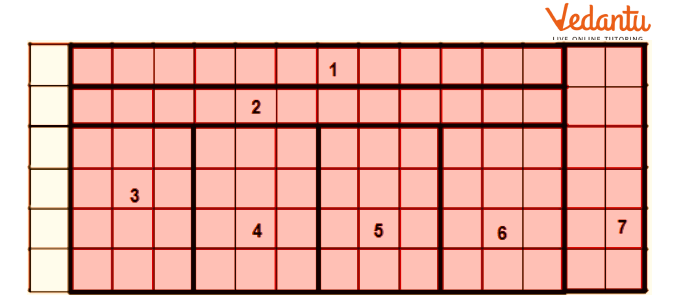
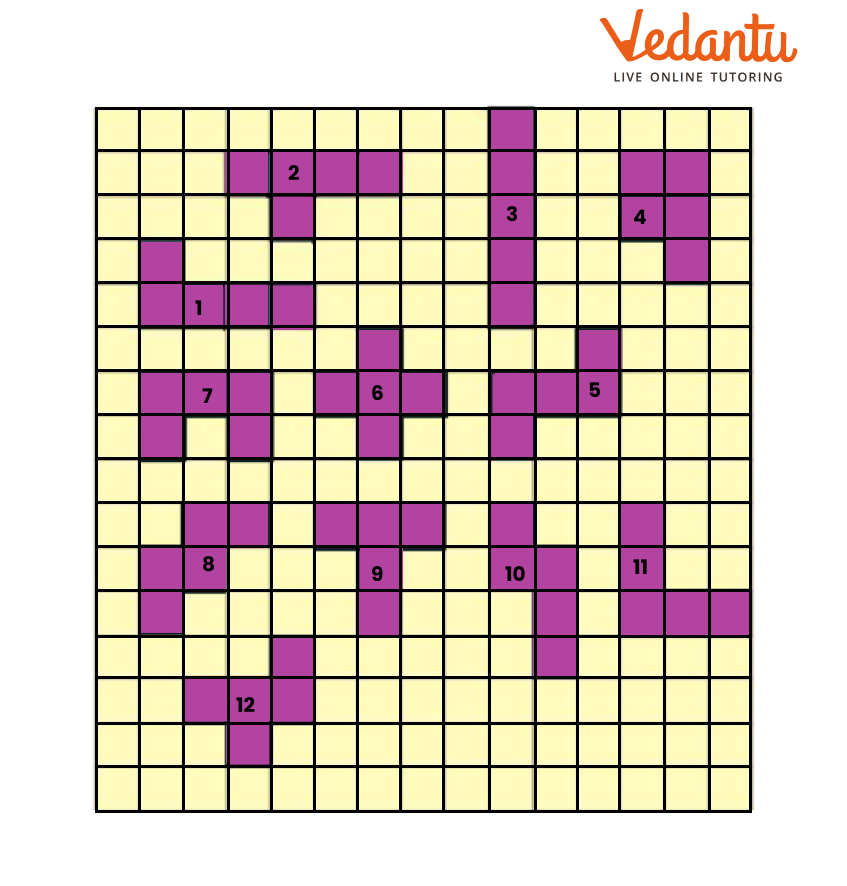
NCERT Solutions for Class 5 Maths Chapter 3 How Many Squares focus on concepts such as counting and identifying squares in patterns, finding the area and perimeter of squares and rectangles, and learning to compare areas using unit squares. The chapter also introduces the method to determine the area of irregular shapes using grid paper as per the CBSE 2025–26 syllabus.
2. How do NCERT Solutions for Class 5 Maths Chapter 3 help students understand area calculation?
These solutions utilize a stepwise approach where students count unit squares inside shapes, use formulas for area and perimeter, and practice estimating areas for irregular shapes using grid methods. This aligns with the CBSE format and develops practical measurement skills.
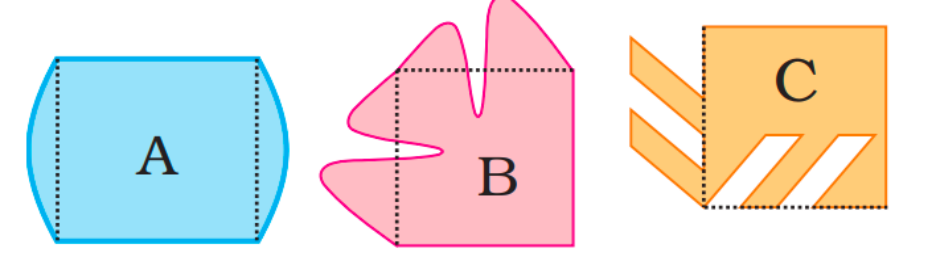
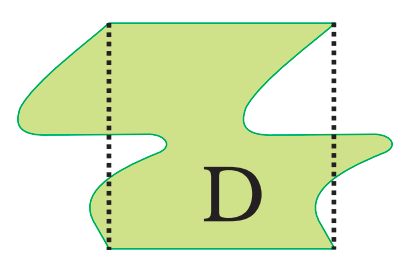
3. What is the method to find the area of irregular shapes using the Class 5 Chapter 3 solutions?
To find the area of irregular shapes using NCERT Class 5 Maths Chapter 3 Solutions:
- Trace the shape on a square (grid) paper.
- Count the number of full, half, and more-than-half-filled squares inside the shape.
- Add full squares, add half-filled as 0.5 each, and more-than-half as 1.
- The sum gives the approximate area in square centimeters.
4. Why is it important to learn about area and perimeter in Class 5 Maths Chapter 3 as per CBSE norms?
Area and perimeter form the foundation of geometry and measurement in higher classes. Understanding these through counting squares and using formulas helps students solve real-life problems involving space, tiling, and boundary calculations as emphasized in the 2025–26 CBSE syllabus.
5. How do NCERT Solutions for Class 5 Maths Chapter 3 explain the difference between area and perimeter?
Area measures the space inside a shape, usually in square centimeters, while perimeter is the total distance around the shape. The solutions provide practical exercises where students compute both for given shapes, clarifying this difference.
6. What should students do if they find two shapes with equal areas but different perimeters in How Many Squares?
Students are taught through examples that shapes can have the same area but different perimeters. They should compare the boundary lengths using a ruler or by measuring line segments to observe how shape arrangement affects perimeter.
7. In NCERT Class 5 Maths Chapter 3, how can children check which of their footprints has a larger area?
Children should trace each footprint on a grid sheet, count the number of unit squares covered, and compare the totals to see which footprint has a greater area, as directed in the NCERT solutions methodology.
8. What common mistakes do students make when solving area-related questions in Class 5 Chapter 3?
Common mistakes include:
- Confusing area with perimeter.
- Counting partial squares incorrectly.
- Not following the formula for area of squares or rectangles.
- Ignoring the units (square cm) in final answers.
9. How do NCERT Solutions for Class 5 Maths Chapter 3 support CBSE exam preparation?
The solutions follow the CBSE exam pattern, providing stepwise answers, practice questions similar to exam formats, and foster conceptual clarity by highlighting the correct problem-solving approaches, which help students score better in tests.
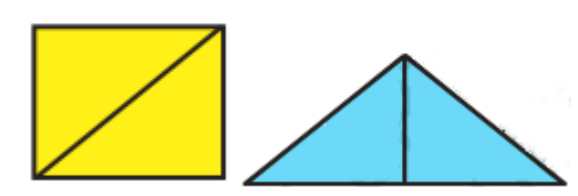
10. What should a student do if two stamps have the same area but different shapes, as seen in How Many Squares Class 5?
Students learn that shapes can look different but still cover the same area. In such cases, the area should be calculated or compared by counting the number of squares or using the length and breadth formula. This develops spatial and geometric skills, critical for future topics.
11. What is the NCERT-recommended formula for finding the area of a square in Class 5 Chapter 3?
The formula given in NCERT Solutions for Class 5 Maths Chapter 3 for the area of a square is: Area = side × side (where the side is measured in centimeters or units as per the question).
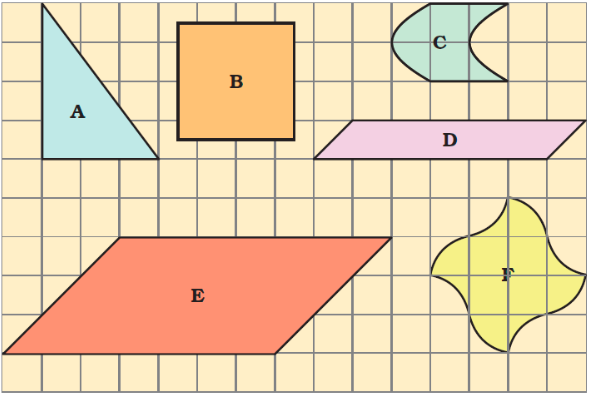
12. Can students use any shape to fill a floor pattern without gaps as discussed in Class 5 Maths Chapter 3?
No, only certain shapes like squares, rectangles, or specific tiles like those shown in the NCERT solutions can tile a floor without gaps. The solutions demonstrate which shapes are suitable for efficient tiling by visual examples.
13. In the context of Class 5 Maths Chapter 3, How Many Squares, what would happen if a student only counts full squares while finding the area?
If only full squares are counted when finding area, the answer will be an underestimate. Proper calculation involves including half and more-than-half-filled squares as partial areas, as per the NCERT guideline for accuracy.
14. How does solving questions from NCERT Solutions for Class 5 Maths Chapter 3 prepare students for higher classes?
Practicing these questions gives students a conceptual base in measurement, area, and perimeter, which are crucial for advanced geometry and mathematics in higher classes following the CBSE curriculum.
15. What are the key learning outcomes after solving NCERT Solutions for Class 5 Maths Chapter 3?
After solving the chapter, students will be able to:
- Identify and count squares in various patterns
- Find area and perimeter of rectangles and squares
- Compare different shapes based on area and boundary
- Avoid common errors and use correct formulas
- Apply measurement skills in real-life contexts