NCERT for Class 7 Maths Chapter 2 - Fractions and Decimals Exercise 2.2

Exercise 2.2 

1.Find:

(i) $\dfrac{\text{1}}{\text{4}}\,\text{of}$

1. $\dfrac{\text{1}}{\text{4}}$

2. $\dfrac{\text{3}}{\text{5}}$

3. $\dfrac{\text{4}}{\text{3}}$

Ans:

(a) Calculating the value,

$\dfrac{\text{1}}{\text{4}}\,\text{of}\,\dfrac{\text{1}}{\text{4}}\text{=}\dfrac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{4}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 1}}{\text{4 }\!\!\times\!\!\text{ 4}}\text{=}\dfrac{\text{1}}{\text{16}}$ 

(b) Calculating the value,

$\dfrac{\text{1}}{\text{4}}\,\text{of}\,\dfrac{\text{3}}{\text{5}}\text{=}\dfrac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{4}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 3}}{\text{4 }\!\!\times\!\!\text{ 4}}\text{=}\dfrac{\text{3}}{\text{16}}$ 

(c) Calculating the value,

$\dfrac{\text{1}}{\text{4}}\,\text{of}\,\dfrac{\text{4}}{\text{3}}\text{=}\dfrac{\text{1}}{\text{4}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{3}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 4}}{\text{4 }\!\!\times\!\!\text{ 3}}\text{=}\dfrac{\text{1}}{\text{3}}$ 

(ii) \[\dfrac{\text{1}}{\text{7}}\,\text{of}\] (a) \[\dfrac{\text{2}}{\text{9}}\] (b) \[\dfrac{\text{6}}{\text{5}}\] (c) $\dfrac{\text{3}}{\text{10}}$ 

Ans:

(a) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 2}}{\text{7 }\!\!\times\!\!\text{ 9}}\text{=}\dfrac{\text{2}}{\text{63}}$ 

(b) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{6}}{\text{5}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 6}}{\text{7 }\!\!\times\!\!\text{ 5}}\text{=}\dfrac{\text{6}}{\text{35}}$ 

(c) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{10}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 3}}{\text{7 }\!\!\times\!\!\text{ 10}}\text{=}\dfrac{3}{70}$

2. Multiply and reduce to lowest form (if possible):

(i) $\dfrac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ 2}\dfrac{\text{2}}{\text{3}}$ 

Ans: 

Multiplying and reducing to lowest form,  

$\dfrac{2}{3}\times 2\dfrac{2}{3}=\dfrac{2}{3}\times \dfrac{8}{3}=\dfrac{2\times 8}{3\times 3}=\dfrac{16}{9}=1\dfrac{7}{9}$ 

(ii) $\dfrac{\text{2}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{7}}{\text{9}}$

Ans: 

Multiplying and reducing to lowest form,  

$\dfrac{2}{7}\times \dfrac{7}{9}=\dfrac{2\times 7}{7\times 9}=\dfrac{2}{9}$

(iii) $\dfrac{\text{3}}{\text{8}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{6}}{\text{4}}$ 

Ans: 

Multiplying and reducing to lowest form, 

$\dfrac{3}{8}\times \dfrac{6}{4}=\dfrac{3\times 6}{8\times 4}=\dfrac{3\times 3}{8\times 2}=\dfrac{9}{16}$

(iv) $\dfrac{\text{9}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{5}}$ 

Ans: 

Multiplying and reducing to lowest form, 

$\dfrac{9}{5}\times \dfrac{3}{5}=\dfrac{9\times 3}{5\times 5}=\dfrac{27}{25}=1\dfrac{2}{25}$

(v) $\dfrac{\text{1}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{15}}{\text{8}}$ 

Ans: 

Multiplying and reducing to lowest form,

$\dfrac{1}{3}\times \dfrac{15}{8}=\dfrac{1\times 15}{3\times 8}=\dfrac{1\times 5}{1\times 8}=\dfrac{5}{8}$

(vi) $\dfrac{\text{11}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{10}}$ 

Ans: 

Multiplying and reducing to lowest form,  

$\dfrac{11}{2}\times \dfrac{3}{10}=\dfrac{11\times 3}{2\times 10}=\dfrac{33}{20}=1\dfrac{3}{20}$ 

(vii) $\dfrac{\text{4}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{12}}{\text{7}}$ 

Ans: 

Multiplying and reducing to lowest form,  

$\dfrac{4}{5}\times \dfrac{12}{7}=\dfrac{4\times 12}{5\times 7}=\dfrac{48}{35}=1\dfrac{13}{35}$

3. Multiply the following fractions:

(i) $\dfrac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ 5}\dfrac{\text{1}}{\text{4}}$

Ans:

Performing multiplication,

$\dfrac{2}{5}\times 5\dfrac{1}{4}=\dfrac{2}{5}\times \dfrac{21}{4}=\dfrac{2\times 21}{5\times 4}=\dfrac{1\times 21}{5\times 2}=\dfrac{21}{10}=2\dfrac{1}{10}$ 

(ii) $\text{6}\dfrac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{7}}{\text{9}}$ 

Ans:

Performing multiplication,

$6\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{32}{5}\times \dfrac{7}{9}=\dfrac{32\times 7}{5\times 9}=\dfrac{224}{45}=4\dfrac{44}{45}$

(iii) $\dfrac{\text{3}}{\text{2}}\text{ }\!\!\times\!\!\text{ 5}\dfrac{\text{1}}{\text{3}}$ 

Ans:

Performing multiplication,

$\dfrac{3}{2}\times 5\dfrac{1}{3}=\dfrac{3}{2}\times \dfrac{16}{3}=\dfrac{48}{6}=8$ 

(iv) $\dfrac{\text{5}}{\text{6}}\text{ }\!\!\times\!\!\text{ 2}\dfrac{\text{3}}{\text{7}}$ 

Ans:

Performing multiplication,

$\dfrac{5}{6}\times 2\dfrac{3}{7}=\dfrac{5}{6}\times \dfrac{17}{7}=\dfrac{85}{42}=2\dfrac{1}{42}$ 

(v) $\text{3}\dfrac{\text{2}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{7}}$

Ans:

Performing multiplication,

$3\dfrac{2}{5}\times \dfrac{4}{7}=\dfrac{17}{7}\times \dfrac{4}{7}=\dfrac{68}{35}=1\dfrac{33}{35}$

(vi) $\text{2}\dfrac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ 3}$ 

Ans:

Performing multiplication,

$2\dfrac{3}{5}\times 3=\dfrac{13}{5}\times \dfrac{3}{1}=\dfrac{13\times 3}{5\times 1}=\dfrac{39}{5}=7\dfrac{4}{5}$

(vii) $\text{3}\dfrac{\text{4}}{\text{7}}\text{ }\!\!\times\!\!\text{   }\dfrac{\text{3}}{\text{5}}$ 

Ans:

Performing multiplication,

$3\dfrac{4}{7}\times \dfrac{3}{5}=\dfrac{25}{7}\times \dfrac{3}{5}=\dfrac{5\times 3}{7\times 1}=\dfrac{15}{7}=2\dfrac{1}{7}$

4. Which is greater:

(i) $\dfrac{\text{2}}{\text{7}}\,\text{of}\,\dfrac{\text{3}}{\text{4}}\,\text{or}\,\dfrac{\text{3}}{\text{5}}\,\text{of}\,\dfrac{\text{5}}{\text{8}}$

Ans:

Calculating the greater term,

$\dfrac{\text{2}}{\text{7}}\,\text{of}\,\dfrac{\text{3}}{\text{4}}\,\text{or}\,\dfrac{\text{3}}{\text{5}}\,\text{of}\,\dfrac{\text{5}}{\text{8}}$                

$\Rightarrow \dfrac{\text{2}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{4}}\,\text{or}\,\dfrac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{5}}{\text{8}}$ 

$\Rightarrow \dfrac{\text{3}}{\text{14}}\,\text{or}\,\dfrac{\text{3}}{\text{8}}$      

$\Rightarrow \dfrac{3}{14}<\dfrac{3}{8}$ 

Hence, $\dfrac{\text{3}}{\text{5}}\,\text{of}\,\dfrac{\text{5}}{\text{8}}$ is greater.

(ii) $\dfrac{\text{1}}{\text{2}}\,\text{of}\,\dfrac{\text{6}}{\text{7}}\,\text{or}\,\dfrac{\text{2}}{\text{3}}\,\text{of}\,\dfrac{\text{3}}{\text{7}}$ 

Ans:

Calculating the greater term,

$\dfrac{\text{1}}{\text{2}}\,\text{of}\,\dfrac{\text{6}}{\text{7}}\,\text{or}\,\dfrac{\text{2}}{\text{3}}\,\text{of}\,\dfrac{\text{3}}{\text{7}}$                

$\Rightarrow \dfrac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{6}}{\text{7}}\,\text{or}\,\dfrac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{7}}$ 

$\Rightarrow \dfrac{\text{6}}{\text{14}}\,\text{or}\,\dfrac{\text{2}}{\text{7}}$         

$\Rightarrow \dfrac{\text{6}}{\text{14}}>\dfrac{\text{2}}{\text{7}}$ 

Hence, $\dfrac{\text{1}}{\text{2}}\,\text{of}\,\dfrac{\text{6}}{\text{7}}$ is greater.

(ii) \[\dfrac{\text{1}}{\text{7}}\,\text{of}\] (a) \[\dfrac{\text{2}}{\text{9}}\] (b) \[\dfrac{\text{6}}{\text{5}}\] (c) $\dfrac{\text{3}}{\text{10}}$ 

Ans:

(a) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 2}}{\text{7 }\!\!\times\!\!\text{ 9}}\text{=}\dfrac{\text{2}}{\text{63}}$ 

(b) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{6}}{\text{5}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 6}}{\text{7 }\!\!\times\!\!\text{ 5}}\text{=}\dfrac{\text{6}}{\text{35}}$ 

(c) Calculating the value,

$\dfrac{\text{1}}{\text{7}}\,\text{of}\,\dfrac{\text{2}}{\text{9}}\text{=}\dfrac{\text{1}}{\text{7}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{10}}\text{=}\dfrac{\text{1 }\!\!\times\!\!\text{ 3}}{\text{7 }\!\!\times\!\!\text{ 10}}\text{=}\dfrac{3}{70}$ 

5. Saili plants \[\text{4}\] saplings in a row in her garden. The distance between two adjacent saplings is \[\dfrac{\text{3}}{\text{4}}\] m. Find the distance between the first and the last sapling. 

Ans:

Given: Saili plants \[4\] saplings in a row where the distance between two adjacent saplings $=\dfrac{3}{4}$m.

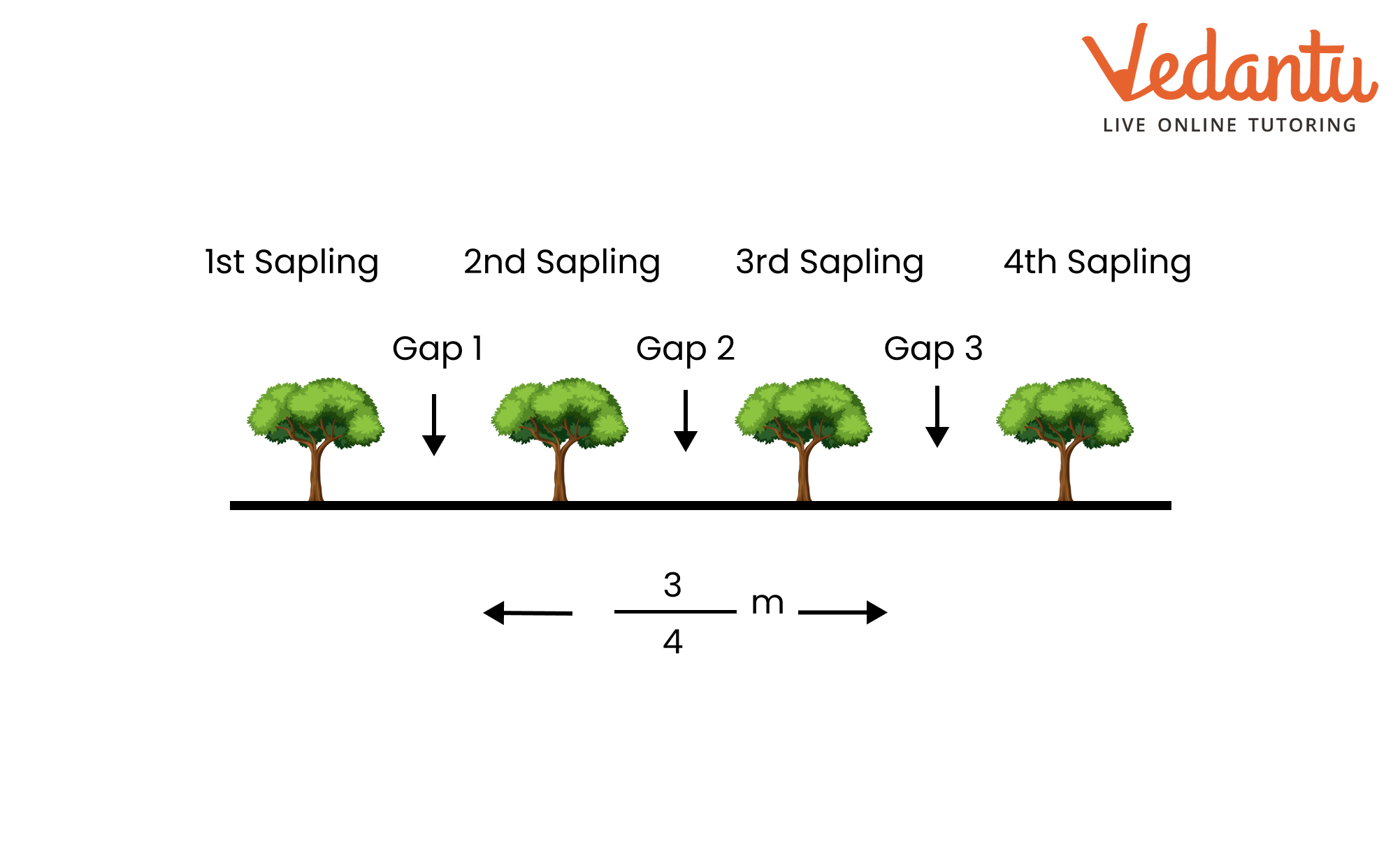
Given: Saili plants \[4\] saplings in a row where the distance between two adjacent saplings $=\dfrac{3}{4}$m

The number of gaps in saplings \[=\text{ }3\] 

Hence, 

The distance between the first and the last saplings$\text{=3 }\!\!\times\!\!\text{ }\dfrac{\text{3}}{\text{4}}\text{=}\dfrac{\text{9}}{\text{4}}\text{m=2}\dfrac{\text{1}}{\text{4}}\text{m}$

Therefore, the distance between the first and the last saplings is $\text{2}\dfrac{\text{1}}{\text{4}}\,\text{m}$

6. Lipika reads a book for $\text{1}\dfrac{\text{3}}{\text{4}}$ hours every day. She reads the entire book in \[\text{6}\] days. How many hours in all were required by her to read the book?

Ans:

Given: Time taken for reading a book by Lipika $=1\dfrac{3}{4}$ hours.

Lipika reads the entire book in $6$ days

Calculating the Total hours taken by Lipika to read the entire book,

$=1\dfrac{3}{4}\times 6=\dfrac{7}{4}\times 6=\dfrac{21}{2}=10\dfrac{1}{2}$ hours.

Hence, it would take $10$ hours to read the book.

7. A car runs $\text{16}$ km using \[\text{1}\] litre of petrol. How much distance will it cover using   $\text{2}\dfrac{\text{3}}{\text{4}}$ litres of petrol?

Ans:

Given: A car covers the distance$\text{=16}\,\text{km}$ in $1$ litre of petrol.

Calculating the distance covered by car in $2\dfrac{3}{4}$ litres of petrol,

Distance$\text{=2}\dfrac{\text{3}}{\text{4}}\,\text{of}\,\text{16}\,\text{km=}\dfrac{\text{11}}{\text{4}}\text{ }\!\!\times\!\!\text{ 16=44}\,\text{km}$

Therefore, car will cover a distance of $44$ km in $2\dfrac{3}{4}$ litres of petrol.

8.(a) (i) Provide the number in the box $___$, such that $\dfrac{\text{2}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\text{=}\dfrac{\text{10}}{\text{30}}$ 

(ii) The simplest form of the number obtained in $___$ is _____.

Ans:

(i) The number inside the box should be $\dfrac{2}{3}\times =\dfrac{10}{30}$

(ii) The simplest form of the number obtained in $\dfrac{\text{5}}{\text{10}}\,\text{is}\,\dfrac{\text{1}}{\text{2}}$

(b) (i) Provide the numberin the box $ ___$ , such that $\dfrac{3}{5}\times =\dfrac{24}{75}$.

(ii) The simplest form of the number obtained in $___$ is______.

Ans:

(i) The number inside the box should be $\dfrac{3}{5}\times =\dfrac{24}{75}$

(ii) The simplest form of the number obtained in $\dfrac{\text{8}}{\text{15}}\,\text{is}\,\dfrac{\text{8}}{\text{15}}$

Conclusion

The "NCERT Solutions for Class 7 Exercise 2.2 Fractions and Decimals" by Vedantu covers essential concepts of adding, subtracting, multiplying, and dividing fractions. It's important to understand how to convert mixed fractions to improper fractions and find the least common multiple (LCM) for addition and subtraction of unlike fractions. Focus on mastering these operations as they form the foundation for more advanced math topics.

NCERT Solution Class 7 Maths Chapter 2 - Fractions and Decimals Other Exercises

CBSE Class 7 Maths Chapter 2 Other Study Materials

Chapter-Specific NCERT Solutions for Class 7 Maths

Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for NCERT Class 7 Maths

Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.