Angle of Inclination: An Overview
The inclination from the x-axis to a line, or slope, on a graph, is measured as the angle of inclination of a slope. Inclined meaning in Physics is used for solving those questions in which a mass or object is sliding from any surface with a slope. This is a measurement of the angle formed between a positive portion of the x-axis travelling counter-clockwise until it touches the slope of the line. It is similar to the measurement of inclination on a graph. If the line's slope is positive, it will pass through the graph's top right quadrant and have an acute angle. If the line has a negative slope, it will go through the top left quadrant and have an obtuse angle.
What is the Angle of Inclination?
On a graph, the distance between two lines is measured by their angle of inclination. This area is typically triangular in form since lines on a graph are frequently drawn at an angle. Since the angles of all triangles are equal, this area between two lines must frequently be expressed by "angles of inclination." Because the angle of inclination and the slope of the line are truly identical, we may utilise it when the slope of a line cannot be calculated in the usual method. The angle of inclination is acute when the slope is positive. The angle of inclination is obtuse when the slope is negative.
Relation between Inclination and Slope
A line's slope on a graph is the ratio of change from the vertical to the horizontal. The letter m is frequently used to symbolise this. A line's slope increases with its steepness. On a graph, a slope that is represented by a negative number indicates that the line is moving downhill rather than upward. The following equation describes the connection between a line's inclination and slope.
\[m = \tan \theta \]
Positive Slope or Negative Slope
How to find the inclination of a line? Let’s suppose we have any line with a coordinate \[({x_1},{y_1})\] and \[({x_2},{y_2})\], then the slope can be calculated as:
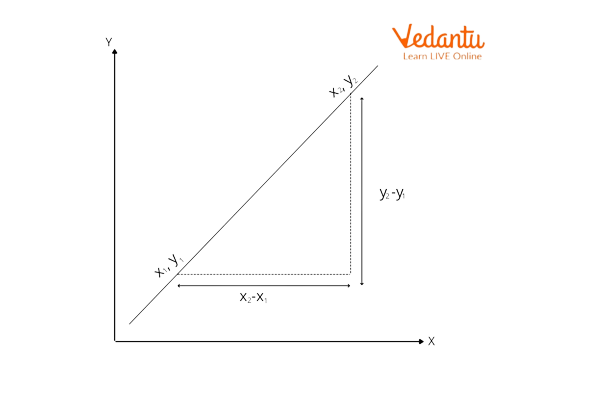
Graph Showing Negative Slope
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
\[\tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
From the above two equations, we can say
\[m = \tan \theta \]
If \[\tan \theta \] is greater than zero, then the angle is acute. In this condition, we can say the slope is positive. If \[\tan \theta \] is smaller than zero, then the angle is obtuse. In this condition, we can say the slope is negative. The above equations are used as the angle of inclination formula.
Inclination or Slope of Horizontal Line and Vertical Line
Inclination or Slope of Horizontal Line
We are aware that a horizontal line in a coordinate plane is a straight line that is either drawn from left to right or right to left and is parallel to the x-axis. As a result, there has been zero net change in the y-coordinates of the horizontal line.
For the horizontal line, the slope is zero.
m = 0.
Inclination or Slope of Vertical Line
We are aware that in a coordinate plane, a vertical line is a straight line that is drawn from top to bottom or bottom to top and is parallel to the y-axis. As a result, there has been zero net change in the vertical line's x-coordinates.
For the Vertical line, the slope is undefined.
m = undefined
Different Types of Slope
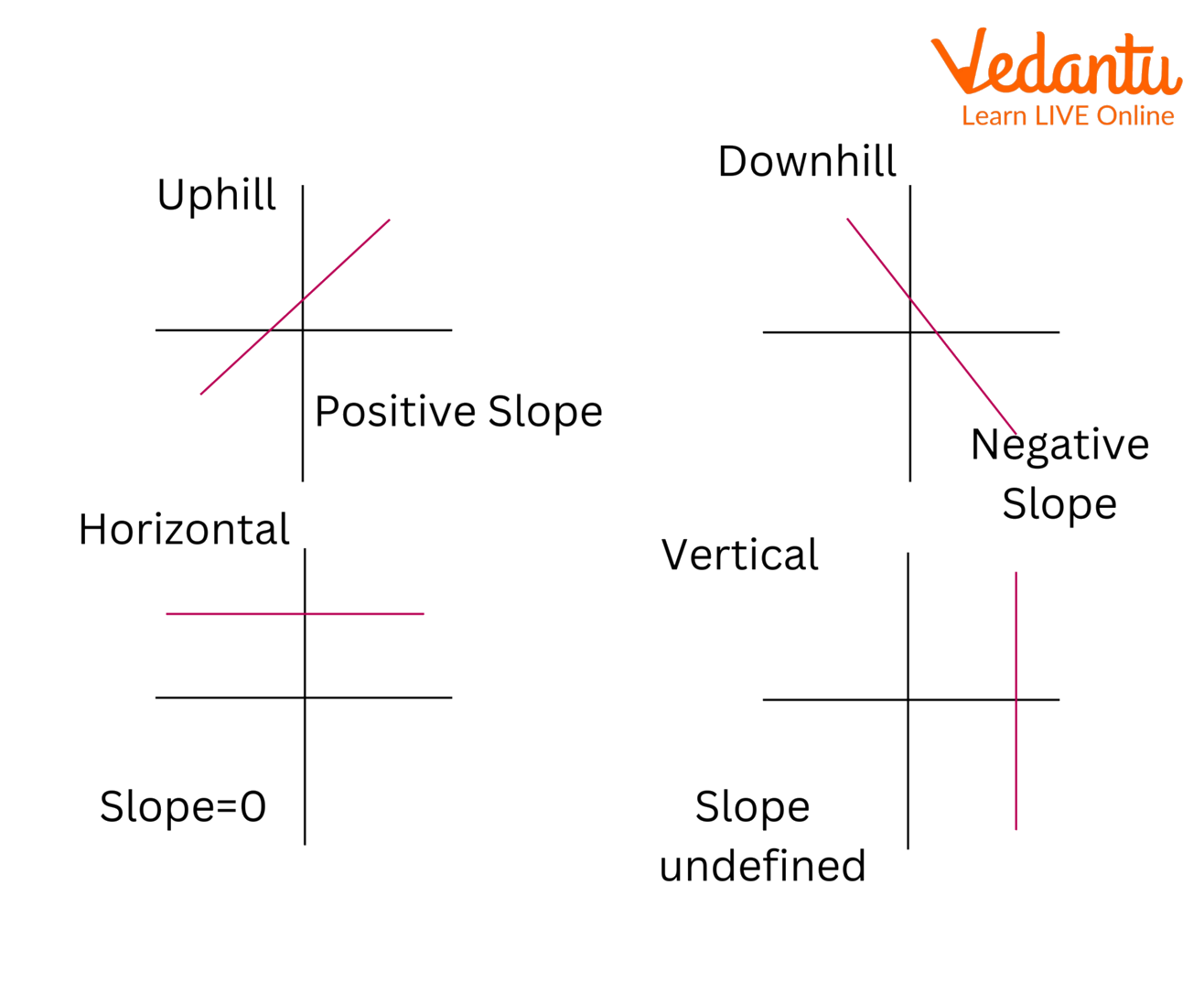
Positive Slope, Negative Slope, Zero Slope, and Undefined Slope
Interesting Facts
On its axis, the Earth is tilted. The Earth's inclination on its axis refers to this tilting of the planet's axis. Days and nights differ in length in different parts of the Earth as a result of the tilted axis of the planet.
The pitch of a roof is represented by its slope. The roof's pitch impacts how much building material will be required to construct it as well as how effectively it will function. A proper pitch will stop the buildup of water and debris. The roof will effectively slide off water and debris.
Solved Problem
1. Find the angle of inclination of a line when the points of the line are given as (2,3) and (8,9).
Solution:
Given, (2,3) and (8,9)
\[\tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
\[\Rightarrow \theta = 135\]
\[\Rightarrow \tan \theta = 1\]
\[\therefore \theta = 45\] degrees.
So, the angle which is made by the angle of inclination is 45 degrees.
2. Find the angle of inclination of a line when the points of the line are given as (3,3) and (9,-3).
Solution:
Given, (3,3) and (9,-3)
\[\tan \theta = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
\[\Rightarrow \tan \theta = \dfrac{{ - 3 - 3}}{{9 - 3}}\]
\[\Rightarrow \tan \theta = - 1\]
\[\therefore \theta = 135\]degrees.
The angle made by the inclined line is 135 degrees.
Summary
The angle of inclination is related to the slope of a line. If any object is placed on an inclined plane, it will start moving due to downward force which is created by the angle of inclination. If we use trigonometric functions, then we can calculate it or we can also use the coordinate point of a line for the calculation. In some natural phenomena, it plays an important role.
FAQs on Angle of Inclination
1. What is an inclined example?
The staircase is usually coupled to an inclined plane in residences, hospitals, and other buildings. People can walk on it and easily pull large things over it because of its smooth surface. Physically handicapped persons who use wheelchairs may also move up and down an inclined plane or ramp.
Another commonplace example of an inclined plane is a playground slide.
Cone and cylinder are the two geometric forms that make up a funnel. The cone's curving portion acts as an inclined plane for any liquid that is put into it.
2. What is the inclined meaning?
An inclined plane, commonly referred to as a ramp, is a flat supporting surface that has one end that is higher than the other and is sloped at an angle. One of the six simple machines is the inclined plane, which is employed to help raise or reduce weight. An imbalanced force causes objects put on an inclined plane to accelerate. The amount of tilt on the surface affects how quickly the object slides down; the more tilt there is on the surface, the faster the object will slide down it.
3. What is the inclination angle of the straight line?
The inclination is positive when measured in an anticlockwise direction and negative when measured in a clockwise direction. The angle that a straight line creates with the positive x-axis when measured counterclockwise to the portion of the line above the x-axis is known as the inclination of the line or the angle of inclination of the line. Usually, the inclination is indicated by θ. If we draw any line parallel to the x-axis, then the angle will be zero of that line with the x-axis. But the angle with the y-axis will be 90 degrees.
